Фрактальная графика. Мир фракталов.

Увидеть мир в одной песчинке И Космос весь - в лесной травинке! Вместить в ладони бесконечность И в миге мимолетном вечность!

Уильям Блейк

Наука стремительно меняет мир. Все окружающее нас, в той или иной степени может быть объяснено наукой. Постоянно появляются новые явления и объекты для изучения, формулируются новые понятия. Одновременно происходит глобальная компьютеризация жизненного пространства человека. Сейчас мы уже не мыслим себя отдельно от компьютеров, телефонов, различных гаджетов. Они целиком и полностью интегрировались в нашу жизнь. Человеческому мозгу и глазу «интересно» смотреть на то, что происходит на экранах этих устройств. Компьютерная графика в данном случае играет не последнюю роль. Порой работа над графикой занимает до 90% времени работы программистов, создающих программы для массового применения. Компьютерную графику подразделяют на векторную, растровую и фрактальную. Одним из интереснейших, быстро развивающихся и перспективных видов

Рис.1 Абстрактные композиции фрактальной графики

компьютерной графики на сегодняшний день является фрактальная графика, своего рода слияние математики и искусства.

Что же такое фрактальная графика? Каждый из нас уже встречался с ней. Это и узоры настенного ковра из советского прошлого, это и многочисленные заставки сайтов с повторяющимися рисунками, капуста Романеско, ландшафт компьютерных игр, рисунок ракушка и многое другое (рис.1)

Фрактальная графика – это графика, которая основана на математических вычислениях. Её базовые элементы - математические формулы, а изображение выстраивается исключительно по уравнениям или системам уравнений. Для того, чтобы понять особенности фрактальной графики, необходимо познакомиться с так называемым «фракталом», объектом, который был открыт относительно недавно, особенности которого и позволяют фрактальной графике решать новые интересные задачи.

В прошлом столетии появились понятия «фрактал», «фрактальная геометрия». Чуть позже понятие «фрактальная графика». Итак, разберемся с понятиями, как и когда они появились.

Фрактал можно рассматривать как структуру, состоящую из частей, подобных целому. Это понятие появилось в 70-х годах 20 века. Ввел его гениальный ученый Бенуа Мандельброт в 1975 году. Само слово fractus заимствовано из латыни, оно означает «дробленый» или «ломаный». Необходимо сказать, что Мандельброт был не первый уче- ный, пытавшийся упорядочить знания об этих необычных объектах. В этой области в 19-20-х веках работали такие ученые, как Пьер Фату, Жюль Анри Пуанкаре, Феликс Хаусдорф, Георг Кантор, Гастон Жюлиа. Они смогли заложить математическую основу для теории Мандельброта. И лишь с появлением компьютеров, появилась возможность в полной мере понять и увидеть, что же такое фрактал.

Мандельброт и его ученики открыли много новых фракталов. Вот что он писал: «Красота многих фракталов тем более поразительна, что открылась совершенно неожиданно: мы хотели построить – с чисто учебной целью – всего лишь математические диаграммы, и можно было ожидать, что они окажутся сухими и скучными. Поэт как-то написал, что Евклид обнаружил красоту, но ведь чтобы научиться по-настоящему понимать и ценить красоту геометрии Евклида, необходимо долго и упорно тренироваться, и, возможно, обладать особым даром. Напротив, трудно найти человека, равнодушного к фракталам» [3].

Изначально к фракталам в среде ученых относились пренебрежительно. Шарль Эрмит, известный математик назвал их монстрами. Серьезно, как к открытию к ним никто не относился. Только благодаря Бенуа Мандельброту фрактальная геометрия стала достаточно уважаемой прикладной наукой. Вот как описана им геометрия Евклида: «Почему геометрию называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или берега моря… Природа демонстрирует нам не просто более высокую степень, а совсем

Рисунок 2. Треугольники Серпинского

другой уровень сложности. Число различных масштабов длин в структурах всегда бесконечно. Существование этих структур бросает нам вызов в виде трудной задачи изучения тех форм, которые Евклид отбросил как бесформен-ные…»[2].

На самом деле слово «фрактал» не имеет строгого определения. Но у него есть определенные свойства, имея которые, фигура может считаться фракталом:

• 1.    Является самоподобной или приближенно самоподобной.

• 2.    Имеет метрическую размерность, превосходящую топологическую.

Основное свойство фрактала - это самоподобие, т.е. самый наймельчайший фрагмент фрактала способен не только воспроизвести его целиком, но и отразить всю информацию о нем. Часть фрактала нередко представляет собой просто уменьшенный целый фрактал. «В основе фракталов, хаоса и степенных законов лежит объединяющее понятие – самоподобие. Самоподобие, или инвариантность при изменении масштабов или размеров, присуще многим законам природы и бесчисленным явлениям в окружающем нас мире. Более того, самоподобие – одна из важнейших симметрий, играющих формообразующую роль в нашей Вселенной и лежащих в основе наших попыток постичь ее» [7].

По способу создания фракталы делятся на группы:

• •    геометрические фракталы

• •    алгебраические фракталы

• •    стохастические фракталы

Классические примеры геометрических фракталов: треугольник Серпинского, драконова ломаная, снежинка

Коха. Этот тип фракталов получился благодаря простым геометрическим построениям. Сначала берется определенная аксиома – набор отрезков. Далее применяются определенные правила к данной аксиоме, которые и преобразуют ее в геометрическую фигуру. К части фигуры также применяются те же правила. Данные итерации могут повторяться сколько угодное количество раз. В конечном итоге мы получаем сложный геометрический фрактал (рисунок 2).

Следующая группа – алгебраические фракталы. Они строятся с помощью алгебраических формул. Примером могут служить: множество Жюлиа, множество Ньютона, множество Мандельброта.

К стохастическим фракталам относится так называемая «Плазма». С помощью этого фрактала благодаря использованию цвета и текстур, создаются горные массивы, карты высот, береговые линии и т.д. (рисунок 4).

Создание фрактальной композиции состоит совсем не в рисовании, а в программировании. Компьютерной графикой управляют уравнения или системы уравнений. При изменении коэффициента, меняется весь рисунок. В результате можно получить совершенно уникальный объект, не уступающий по замысловатости работе художника-абстракциониста. Получаются сложные изображения, которые очень похожи на природные объекты, фантастические горные и лесные ландшафты для компьютерных игр, виртуальной реальности, книжных иллюстраций. Это так же могут быть различные текстуры, фоновые изображения и многое другое. При создании графических объектов используется все множество приемов: симметрия, асимметрия, диагональ, вертикаль, горизонталь.

Рисунок 3. Алгебраические фракталы

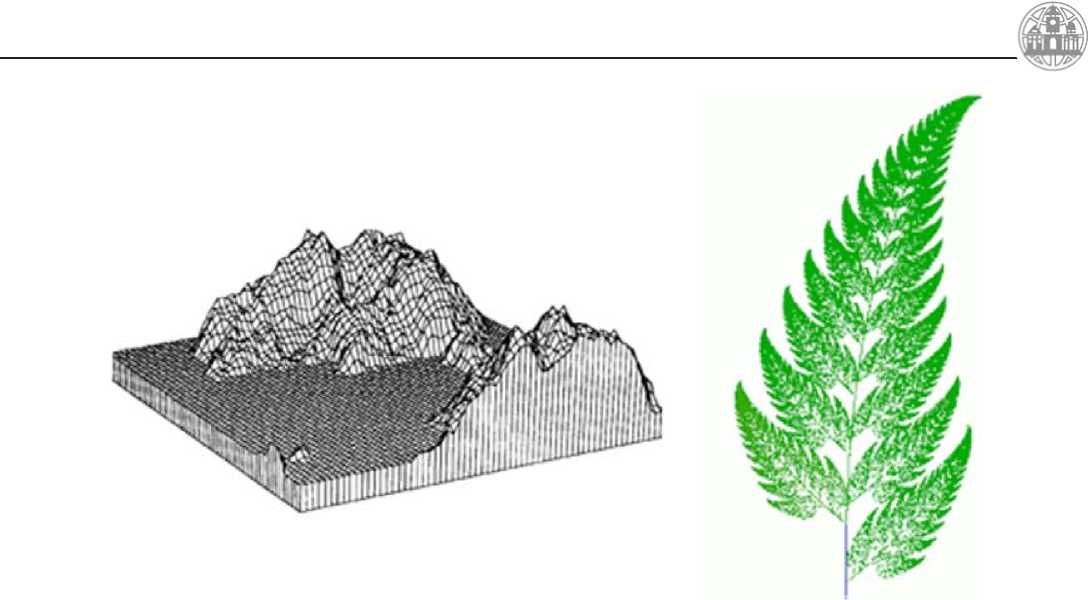
Рисунок 4. Стохастические фракталы

Для создания изображения в качестве элемента фрактальной графики используется треугольник. Задаются параметры точек, их количество. Далее можно использовать различные дополнительные действия:

• •    повороты и растяжения;

• •    группировка объектов;

• •    преобразование цветов;

• •    изменение формы всего объекта или отдельных его частей.

На данный момент существуют следующие программы, с помощью которых можно генерировать фрактальные изображения: Apophysis 3D, Apophysis 7X, Chaotica, Ultra Fractal, Art Dabbler. Какие-то из этих программ могут использоваться новичками для знакомства с фрактальной графикой, а какие-то уже профессионалами. Например, в программе Ultra Fractal фрактальная графика выполняется не только в виде изображения, но и в виде анимации.

В использовании фрактальной графики есть как плюсы, так и минусы. К минусам можно отнести небольшой спектр создания объектов изображений и небольшое количество «материнских» фигур. Сюда можно отнести также и малую освоенность данной технологии. Хотя это можно считать и плюсом, так как для исследователей открываются горизонты открытий в этой области. Плюсы более наглядны: у фрактала при большом изображении достаточно небольшой размер файла; при бесконечном увеличении увеличивается и сложность картинки; относительно легкое создание сложных композиций; отсутствие аналогов в построении сложных фигур, которые состоят из подобных друг другу элементов (вода, деревья, горы, облака и т.д.), а также реалистичность создаваемых объектов.

Фрактальная графика уникальна. У нее нет аналогов. Малая часть фрактала может передать информацию обо всем объекте, так как он самоподобен. Для того, чтобы начать творить, не нужно большое количество объектов, необходима только формула. Фракталы особенно часто встречаются в природе. Мы видим их вокруг себя постоянно, не обращая на них внимание. Человеческому взгляду нравится природные изгибы, детали, элементы, такие как облака, горы, русла рек, прожилка листьев, деревья, камни, раковины моллюсков и т.д. Принцип фракталь-ности заложен в самой природе. Именно поэтому реализм фрактальной графики так же не имеет аналогов. «Создание компьютерных моделей природных явлений и процессов позволяет понять причины возникновения динамического хаоса, фрактальности реальных объектов, условия зарождения и развития самоорганизующихся систем, кинетический характер фазовых превращений в открытых диссипативных структурах и многие другие характеристики реального мира» [4]. Скорее всего, только спустя время, мы сможем понять, насколько важным и ценным для человечества явилось открытие фракталов.