Фрактально-кластерная теория и термодинамические принципы управления сложными системами

Самарский научный центр РАН

В статье изложены основы фрактально-кластерной теории, включающей фрактально-кластерные соотношения, динамические уравнения эволюции фрактально-кластерной системы и критерии управления. Показано, что критерий эффективностифрактально-кластерной системы является более чувствительным индикатором качества структурного управления сложной самоорганизующейся системой, чем полная эффективность и информационная энтропия. Проведен анализ устойчивости состояния и трансформирования фрактально-кластерных соотношений.

Основой метода управления, анализа эффективности управления и функционирования самоорганизующейся системы в исследовании приняты термодинамический метод и фрактально-кластерные соотношения (ФКС) [1].

В результате длительных многолетних исследований [1] удалось доказать, что в любых системах: технических, биологических системах, прошедших эволюционный путь развития, системах машина-человек всегда имеется пять основных кластеров. Это энергетический (Кэ), транспортный (Ктр), технологический (Кт), экологический (Кэ) и информационный (Ки) кластеры, имеющие определенные (идеальные) значения, выраженные в процентах или долях целого для экстенсивного параметра системы (время, деньги, масса и т.п.). Для энергетического кластера это значение составляет 38%, транспортного - 27%, экологического - 16%, технологического -13%, информационного - 6%.

Каждый из пяти кластеров имеет пять подкластеров, например: в энергетическом -энергетическая поддержка самой энергетической системы, энергетическая поддержка транспорта, экологии, технологии, информатики и т.д. И остальные подкластеры соответствующим образом подразделяются на пять подкластеров следующего уровня. Для анализа функционирования биологических, технических и антропогенных систем, как правило, достаточно второго или третьего уровня ФКС.

Такая кластеризация [1] позволила производить оценку функционирования сложной системы. Однако, теории на основе ФКС создано не было. Поэтому целью данного исследования являлась разработка теории структурного управления сложными системами на основе синтеза экономики, ФКС и неравновесной термодинамики.

Представленная фрактально-кластерная теория включает в себя:

• 1)    фрактально-кластерные соотношения (ФКС) В.П. Бурдакова [1];

• 2)    динамические уравнения эволюции фрактально-кластерной системы [2];

• 3)    фрактально-кластерные критерии эффективности управления системой;

• 4)    анализ устойчивости сложных самоорганизующихся систем.

Динамические уравнения ФКС

Эволюция любой экоматермической системы n-го уровня из неидеального кластерно-фрактального состояния в идеальное может быть записана в виде следующей системы уравнений [2, 3]:

K i (t) = K 0 + £ и_у(е _y,t ) ■ K j ;

j = 1

K_y(t) = K 0 + U_y(e _y,t ) ■ K 0 ;

K m.® = K 0m + U ijm ⁽е_У т , tУ K m ;

К (t) = K0 + U    (e    ,t)- K0 ;

ijm...n               ijm...n          ijm...n ijm...n ,           ijm...n

555   5

XXX-X K^ = i,           (5)

i = 1 j = i m = i n = 1

где U_ij

Z K

[ K 0

U ijm...n

tv- ideal

_1Jm-n

K ⁰

^ ijm...n

)

- 1 f j (t) = e , _jf , _J(t) ;

J

• A. (t) = e- f (t)

ijm...n V / ijm...n ijm...n V /.

J

Кластеры и подкластеры любого уров ня есть положительно определенные вели- чины к, > 0; Kij > 0; Kijm...n > 0.

На функции f(t) наложены следующие краевые условия:

^fijm^(t) f ^{Д 0} , ^П р ^{и t Д 0} .

f (t)

ijm..n \ / fj(t) fijm(t) f (t)

ijm...n V / д 1, при t ^ tfm.

Безразмерное время эволюции подкластеров определяется:

t =

t

t 0

t rm-t0’ и и

t -10.

X _______Um t Г _f0 ;

^t ijm ^t ijm

t — t ijm...n f _ + 0

L ijm...n uijm...n

0    0      0 fin fin fin где t                        - начальные и д ij , ijm , ijm...n , ij , ijm , ijm...n конечные значения первого, второго и (n-1) уровня.

В уравнениях (1)-(5) безразмерные величины определяются следующим образом:

к,- К,/Ку;   k,= к,/ку;

K ijm = K ijm /К , ; K jm,.,. = K ijm...n/ K_y.

Индексы i, j, m... n изменяются в пределах от 1 до 5 и соответствуют 1 - символу "э" - энергетика, 2 - "тр" - транспорт, 3 - "эк" -экология, 4 - "т" - технология, 5 - "и" - информатика.

Uy, U jm , U_{9m n} - управляющие функции для подкластеров первого, второго и (n-1)

К ideal ideal        ideal ij , K ijm .-Kijm...n - идеаёьНые относительные значения подкластеров первого, второго и (n-1) уровня, а V 01 V 0 V 0

K ij , K _ij_m .... K _ij_m..._n - начальные относительные значения соответствующих подкластеров.

Уравнение (5) представляет собой аналог закона сохранения для фрактальной системы.

Энтропийно-кластерный метод управления структурой сложной системы

Предложенные в [2, 3] методы оптимизации управления ФКС опираются на интуитивные или жестко формализованные понятия и аналогии. В связи с выше сказанным логично сформулировать критерий эффективности управления матрицы ФКМ на основе фундаментальных принципов термодинамики устойчивых состояний.

Рассмотрим матрицу идеальных состояний ФКМ (табл.1).

Первая строка и первый столбец идеальной матрицы дают количественную информацию об общей доле энергетических ресурсов системы, которая составляет ~ 61,5% , то есть является основным определяющим фактором эффективности функционирования системы:

Таблица 1. Таблица идеальных значений

K i		К Ij
Ê 1	0,38	0,1440	0,1026	0,0608	0,0494	0,0228
Ê 2	0,27	0,1026	0,0729	0,0432	0,0351	0,0162
Ê 3	0,16	0,0608	0,0432	0,0256	0,0208	0,0960
Ê 4	0,13	0,0494	0,0351	0,2080	0,0169	0,0780
Ê 5	0,06	0,0228	0,0169	0,0960	0,0780	0,0036

___        5 ___        5 ___

К у = Z К_ц + £ К. = 61,5%.   (8)

j = 1          I = 2

Это число очень близко к так называемому "золотому" сечению Н0 = 0,618 известному из многочисленных публикаций как основа красоты и гармонии как в природных, так и в антропогенных явлениях.

Фрактально-кластерная матрица (ФКМ)

{к,}

несет информацию об энергетическом состоянии исследуемой системы. В связи с выше сказанным представляется целесообразным энтропийный подход к анализу управления фрактально-кластерной системой.

Связь между элементами ФКМ и информационной энтропией Н позволяет найти критерий управления ФКМ с целью оптимальной эволюции из неидеального состояния системы (ФКМ неидеальные) в идеальное состояние (ФКМ - идеальные), при этом сумма элементов ФКМ первого столбца и первой строки (8) переходит в их идеальное ж^нте^бс^—чобЖотс^^   энт- ропииН

H = ^ K ij + ^ K ii ^ U ij ^ j = 1           i = 2

^ £ K ideal + ^ K iideal = H 0 = 0,618. (9) j = 1               i = 2

Таким образом, вводится гипотеза об определении условной энтропии (или квазиэнтропии) ФКС (9), опирающаяся на обобщение опытных данных по эволюционирующим системам [1] и структуре ФКМ.

Структура ФКМ сложной системы фрак-тальна: это цепочки повторяющихся подкла стеров, самоподобных по своей структуре. Как известно, изображение фракталов получается за счет итерационных процессов. Простейшим итерационным процессом является ряд Фибоначчи.

Оказалось, что ключом к управлению фрактально-кластерной матрицей (ФКМ) является знаменитый ряд Фибоначчи (0, 1,1,2, 3, 5, 8, 13, Un... Un+1), в котором каждая последующая цифра равна сумме двух предыдущих. Замечательным свойством ряда Фибоначчи является то, что по мере увеличения чисел ряда отношение двух соседних чисел ряда асимметрически приближается к точной пропорции "золотого" сечения - основе красоты и гармонии как в природных, так и в многочисленных антропогенных проявлениях:

lIm-U^ = H = 0,618 . (10) n . т j ⁰

^Un + 1

Правило "золотого" сечения было известно еще в Вавилонии и Древнем Египте. Пропорции пирамиды Хеопса, других произведений древнего искусства красноречиво свидетельствуют об этом.

Ряду Фибоначчи соответствуют многообразные явления структурирования в природе и обществе: размещение семян в цветах, сердечная деятельность, структура моллюска Наутилус и т.д.

В связи с выше сказанным возникла гипотеза об оптимальном управлении ФКМ при помощи ряда Фибоначчи. Но ряд Фибоначчи используется не тривиально сам по себе. Для управления ФКМ используется аппроксимация итераций ряда Фибоначчи. При этом итерации соответствуют отрезкам времени, кратным периоду затухания колебания, то есть аппроксимация итераций ряда Фибоначчи является шаблоном для управления матрицы {uij} (рис-1).

Управляющая матрица { U ij } при одинаковых временах начала и конца эволюции t⁰ = t⁰ = const и t f” = t f” = const, прини- ^{lj jl                               lj jl                     2}

мает вид:

Uj = (к■'e•7кa - 1)f (t -1,).(11)

Функция f ( t -1₀ ) удовлетворяет следующим условиям:

f (0)= 0; f (tfin -1, ) = 1,(12)

где функция f ( t -1₀ ) кусочно-дифференцируема. Аппроксимация итераций ряда Фибоначчи (рис.1) дает следующее выражение:

H f (t - to )==

Ho

+ Ho • exp(- a(t -10 ))x cos(p(t -10)+ ф0), (13) при начальной фазе ф0 = 0, H0 = 0,618 a = 1,05, t0 = 1.

Выражение (13) не удовлетворяет начальным условиям при t = t0. Для удовлетворения второго граничного условия введем новую управляющую функцию U на отрезке времени от нуля до некоторого t:

^U * ^{( t -} t a ) = ^{1 - ex}P ^(- p ^{( t -} t a )) ,    ⁽¹⁴⁾

и осуществим сшивку решений для U ( t -1₀ ) :

^U1 ^{( t} - t 0 ) = ^{f ( t} - t 0 )           7

t

( u * ( t -1 0 ) ) = f' ( t -1 „ ) при

Видно, что управление U * ( t -1₀ ) удовлетворяет условию (12) при t = t₀. После несложных преобразований получаем систему трансцендентных уравнений:

ln(- coSMt_ - to )]• Ho) б-

СШИВКИ o ln

^cosn(t СШИВКИ ^- t o У Ho

= tgMt сшивки ^- t o ))

, (16)

^C0SMt СШИВКИ - t o К < ⁰ где                       ^o

Численно из уравнений (16) определя ется значение t и показатель В . Оказа-сшивки лось, что t - to = 1,19; В = 1,53.

На рис.2 показана эволюция кластеров с управлением по (13, 14).

В связи с данным фактом представляет интерес сравнение решения для управляю-

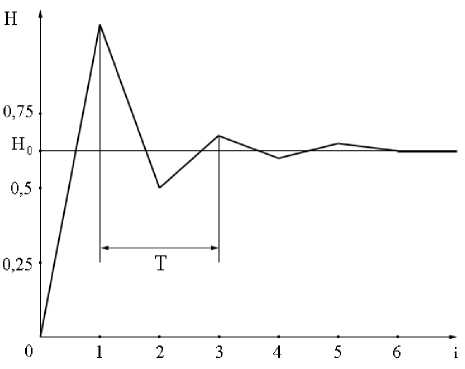
Рис.1. Итерация членов ряда Фибоначчи i - номер итерации, T = 2 - период, Н ₀ =0,618 - "золотое" сечение

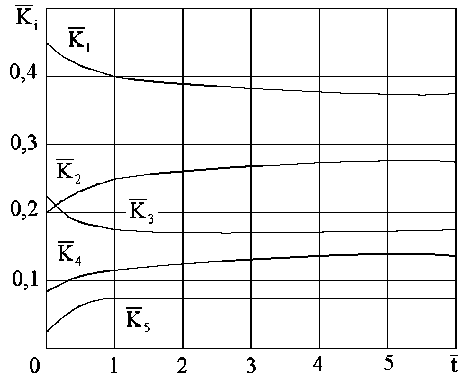
Рис.2. Эволюция кластеров по ряду Фибоначчи для U * * 1 - exp ( - в • ( t - 1₀ )) и матрица ФКС

щей функции U * по формуле (17) с аппроксимацией итераций ряда Фибоначчи (13):

t² • exp l

2 g ²

U ( t ) =<

0 < t < t сшивки,

1 + H₀ • exp ( — б ( t - 1 )) - cos ( n ( t - 1 ))

t < t < 1. сшивки           ’

Решение системы трансцендентных уравнений определяет 1_сшивки и в при фиксированном значении = :

t² • exp l

сшивки

= ¹ + ^H 0 • ^ex P ^(— a ( ^t с_Шивки

^{1 )) c0S} • ( л ( 1 _СШШивк

<

^2t сшивки • ^ex P l

сшивки

—

в

' ^ • ^ex p |

2g       I

сти управления D^ фрактально-кластерной матрицы использовался подход Ф. Хаусдорфа. В отличие от чисто фрактальных структур фрактально-кластерные n-мерные матрицы ФКМ(п) имеют существенное отличие от геометрических фрактальных структур, так как количественные распределения по подкластерам любого уровня могут отличаться от идеального распределения и тем самым изменяется качество системы. Однако все перераспределения в кластерах и подкластерах любого уровня подчиняются законам сохранения (5).

Поэтому предлагается следующий алгоритм определения критерия эффективности фрактально-кластерной n-мерной матрицы ФКМ(п).

Фрактально-кластерные критерии эффективности управления определяется по формуле:

сшивки

в

= H ₀ a • ex]

сшивки

в

сшивки

в

в

_^{— H} 0 • ^S in ⁽ Л ⁽ t с_Шивки ^{— 1 ))- ex} p ( ^a вшивки ^— 1 )) ■

D эфф =

5    5    5       5

logXES -2 i- i=1 j=1 K=1 m=1

logN

Пр^и вшивки = ^{1 пе}р^вое ур^авн^ен^{ие (19)} обращается в тождество при любых в и о.

Таким образом, получено энтропийнокластерное решение по структурному управлению сложной системой. При этом критерием оптимизации управления сложной системы не являются общепринятые критерии - максимизация или минимизация издержек функционирования системы. Критерием оптимизации управления в предлагаемой теории является минимизация отклонения управления системой от решения (17, 18), что соответствует бескризисному развитию сложной системы, основанному на фундаментальных принципах термодинамики и обобщении законов структурной эволюции широкого класса эволюционирующих систем .

Фрактально-кластерные критерии эффективности управления сложной системой

Для определения критерия эффективно где ФКМ является m-мерная матрица.

В формуле (20) величины дi, д*, д i|K m подсчитывается по соотношениям:

*

ДijK...m

= 1 —

/ ideal        \2

KijK...m    1

КТ^{— 1}

^ ijk...m

Полная эффективность функционирования фрактально-кластерной системы определяется согласно [1] следующим образом:

У 1 X 1 ту ideal —1   (ту ideal ту । з =1 — 2К з* V(Ki  — Ki)  , (22)

i=1

где у i - эффективность i-го кластера определяется по формуле:

⁵ ___                / /       " ZZ \ 2

1 X ¹ Л7 ideal    п—1    (ту ideal ту ।

^з* = ^1— 2 ^Kij    • ^зу \^{(K — K}ij) , (23)

j=1

Расчет подкластерных эффективностей у ij m (m-1)-уровня начинается с последнего (m-1)-уровня. Номер уровня меняется следующим образом:

Таблица 2. Сравнительный анализ управления муниципальными структурами

Наименование структуры Энтропия Критерий эффективности Dэфф Полная эффективность з У Относительное отклонение от идеального е н е D е з Муниципальные структуры Московской о оласти 1990 г. 0,360 0,1132 0,8300 41,7% 88,6% 17% 1993 г. 0,564 0,8755 0,9690 8,7% 12,5% 3,1% 1996 г. 0,407 0,7227 0,9257 3,4% 27,8% 7,5% Municipal Department USA, t. Nessua 1993 г. 0,603 0,9700 0,9900 2,42% 3% 1% 1994 г. 0,6156 0,9875 0,9957 0,4% 1,2% 0,4% m -1 < n < 1.

Для определения эффективности управления предложен обобщенный критерий функционирования самоорганизационной системы:

X =

н • П эф • з ^У Н о • П эТ

где Н - информационная энтропия, вычисляемая по (9), Но = 0,618 - "золотое сечение".

Формула (25) представляет собой кластерно-энтропийный критерий управления фрактально-кластерной системой.

В качестве примера в таблице № 2 приведен фрактально-кластерный анализ управления муниципальными структурами для Московской области и муниципального департамента г. Нешуа США. Из данной таблицы видно, что для американского муниципального департамента ФКС практически идеальны, критерий эффективности управления Пэфф и полная эффективность системы близки к 100%. Для муниципальных структур Московской области наиболее удачным с точки зрения управления является 1993 г.

Обобщенный критерий X для г. Нешуа США максимален, что свидетельствует об оптимальности управления.

На рис. 3 показаны различные сценарии топологических структур ФКМ для различных временных этапов эволюции ФКМ к ее идеальному значению.

Анализ устойчивости состояния и трансформирования сложной системы

Используя результаты и основные положения термодинамики структуры [4] и неравновесной нелинейной флуктуационно-диссипативной термодинамики [5], проведен анализ устойчивости сложных саморазвиваю-щихся систем.

t = 0,5; ф = 72°                                 t = 1; ф = 72°

Рис.3. Эволюция ФКС шестого уровня ф = 72 °

Рассмотрим кластеры { К .} и подкластеры { К у}, составляющие ФКС, как случайные внутренние параметры K. (t), К. (t), то есть изменяющиеся флуктуационным образом. Если система изолирована, то информационная энтропия H ({ к у}) не убывает со временем. Однако флуктуационная составляющая информационной (условной) энтропии Н ( к . (t)) может убывать на величину, не превышающую k (k = 1,38 • 10 23 ——) кг

(k - постоянная Больцмана).

V ( дН ( K_g ( t ) )) * <  k .        (26)

Выражение (26) представляет собой микронарушение II начала термодинамики для ФКС.

Усредненные значения подкластеров по некоторому интервалу времени ф равны:

5                 / 5

Е ( к Е ^к .

j = 1                \ j = 1

ф__

= Гк6№/ф

0             . (27)

Условная энтропия Н (A(t)) ФКС в случае несимметричной ФКМ имеет следующий вид:

/         5   \        ___ 5  

H ( A ( t )) = K 1 + Е К = (^) + Е (К_ч), (28)

\        j= 2      /                j = 2

где A (t) - усредненные внутренние парамет

H = 2(К1) - (К,) .

В соответствии с критерием термодинамической устойчивости [4] определим второй дифференциал условной энтропии Н для симметричного случая:

²Н                        2

д²Н = ——у ( д К 1 ) = - 2 ( д К ) <  0 .(32) д( к^

Таким образом, для состояний, близких к ветви термодинамического равновесия в симметричном случае ФКМ, второй дифференциал энтропии д²Н отрицателен, то есть ФКС устойчива.

Граница потери устойчивости для симметричной ФКМ д²Н = 0 реализуется только при д(К 1) = 0 , то есть при полном отсутствии флуктуаций энергетического кластера (К1> .

Во всех остальных случаях при симметричной ФКМ при состояниях, близких к ветви термодинамического равновесияудовлет-

• ^{1                    1}          д²Н < 0.

ФКМ. Второй дифференциал условной энтропии в несимметричном случае ФКМ имеет вид:

Д2Н ((К), (K21), (K22), (K23), (K24 )) = ры, ( ) - знак усреднения по некоторому про

межутку времени ф существенно меньшему времени эволюции Т из начального состоя

д 2 H д( K 1)²

(дК )2+Е ^HH ккл + j=2 dKj1

ния { к ⁰ } в конечное (идеальное) состояние

у— 1 in(ideal) системы { Ку /

„ д ^f д н

+ 2

д( K ij ^д( j

• д(к_л) (д(К 1 ))+

. (33)

/— п \       /— \ fin(ideal)

ф << T (K i>) ^ (Kj)     .    (29)

+2ЕЕ i=2 j>i

д ² H

д( K iiM K- i)

ä K i1 ä K j1

В симметричном случае подкластеры

(К определяются по соотношениям:

(Kij) = (К,) и (Kij) = (Ki)• (Kj), т.е.             (K9) = (KJ .           (30)

Условная энтропия в этом случае равна:

Второй дифференциал условной энтропии д²Н определяется в случае независимости энергетического кластера (К1) и энергетических подкластеров к kJ, (К 13 / ,

К ₁₄) и \К ₁₅) следующим образом:

д²Н = 0 ,            (34)

то есть даже при наличии флуктуаций имеет место нейтральная устойчивость эволюции сложной системы.

В случае линейной зависимости (К 1

и энергетических кластеров К 12 , К 13

К14^ и ^К15^ также имеет место нейтраль ная устойчивость.

В случае нелинейной зависимости под кластеров

{КД (i>1)

от энергетического

кластера могут возникать как устойчивые, так и неустойчивые режимы эволюции фрактально-кластерной матрицы ФКМ сложной системы, то есть:

< 0

д²Щ = 0

- устойчивый режим

- нейтральная устойчивость. (35)

> 0 - неустойчивый режим

Проведенный выше анализ структурной устойчивости сложной системы на основе обобщенной термодинамики необратимых процессов И. Пригожина [4] и предлагаемой фрактально-кластерной теории относится к состояниям, близким к термодинамической ветви равновесия, то есть к линейной термодинамике необратимых процессов.

Критерием устойчивости для сложных систем, соответствующих понятию "диссипативных структур" И. Пригожина, является квадратичная знакопеременная форма, называемая производством приращения энтропии [4]. Для устойчивых диссипативных структур производство избыточной энтропии есть величина положительно определенная:

Р [ дН ] > 0 , ⁽³⁶⁾

где дН =

дН            дН ,

ХМ+ 1    ^д

\ ^К1/           j = 2 ^^K ij)

Как отмечено в [4] однозначно знак производства избыточной энтропии в общем случае определить невозможно. Для конкрет ных систем необходимо использование феноменологических законов для определения знака Р[дН].

Рассмотрим вопрос об устойчивости траектории перевода сложной системы из произвольного в идеальное состояние в соответствии с основными положениями фрактально-кластерной теории. Очевидно, что через две точки в фазовой плоскости энтропия - время (H-t) могут проходить как устойчивые, так и неустойчивые траектории трансформирования системы с точки зрения фрактально-кластерной теории.

Рассмотрим фрактально-кластерную структуру сложной системы, находящейся в состоянии, близком к термодинамической ветви равновесия, то есть при анализе эволюции можно использовать линейную термодинамику неравновесных процессов.

В соответствии с данным фактом можно использовать теорему о минимуме производства энтропии [4].

Для простоты рассмотрим симметричную фрактально-кластерную матрицу (ФКМ) топологической структуры сложной системы, тогда энтропия системы определяется по (31).

Используя теорему И. Пригожина о минимуме производства энтропии [4], определим вид функции f ( t ) из условия нейтральной устойчивости:

dP_o D dH dt ’где dt . (37)

Выражение трансформационной функции f ( t ) , осуществляющей перевод из произвольного в идеальное состояние фрактально-кластерной структуры сложной системы, по траектории нейтральной устойчивости имеет следующий вид:

f ( t ) = { ехр ( б ) - 1 } ¹ ( ехр [ б • t ] - 1 ) .   (38)

В общем случае ненулевой правой части в выражении для производства энтропии получаем следующее выражение для трансформационной функции f ( t ) :

f ( t,e ) = - -t +

а

+ ^f 1 + -1- ( exp ( a ) - 1 )^{- 1} ( exp ( a ■ t ) - 1 ) . (39)

I a J

При параметре е, стремящемся к нулю, f ( t,e ) переходит в решение для f ( t ) при нейтральной устойчивости:

limf ( t,e ) = f ( t ) .            (40)

е ^ 0

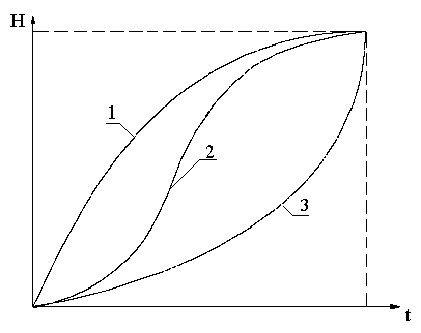
Рис.4. Управление ЭС как функция Н от t

Выражение для функции f ( t,e ) соответствует следующим качественно различным режимам трансформирования топологической фрактально-кластерной структуры сложной системы из неидеального в идеальное состояние:

г = 0 - трансформирование сложной

е

системы по траектории нейтральной устойчивости > 0 - неустойчивая траектория трансформирования сложной системы

< 0 - устойчивая траектория трансформирования сложной системы

В качестве первого примера иллюстрации полученных результатов по анализу устойчивости процесса трансформирования сложной системы из произвольного состояния фрактально-кластерной структуры рассмотрим рис.4, где изображены три различных траектории трансформирования структуры экономических систем:

1) с большими градиентами (шоковые

реформы)

fу < ^ dt

0 -

ет устойчивый ( dP/dt < 0 ) и неустойчивый ( dP/dt > 0 ) характер, а третий режим трансформирования системы неустойчив.

Таким образом, медленное градуированное структурное реформирование с точки зрения фрактально-кластерной теории является неустойчивым.

Данный факт имеет подтверждение на примере рыночных преобразований стран бывших участников Варшавского пакта и стран СНГ.

Математическое моделирование (рис.5) и статистические данные [6] по ВНП, бюджетному дефициту, темпам инфляции показывают, что в странах с шоковой терапией экономики (Польша, Чехия, Словения, Эстония, Латвия) имеет место быстрое выздоровление экономики - за 4 года преобразований возникает профицит бюджета, то есть темпы инфляции снижаются до приемлемых цифр. У стран, проводящих реформы в виде неинфляционного градуализма (Венгрия, Словакия) имеет место медленный темп выздоровления экономики по сравнению со странами

2) с переменными градиентами (переход

ные экономики)

f Г >

^ dt

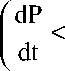
3) с небольшими градиентами (медлен

ные реформы)

Л1Р А

> 0

I ^dt J

Первый режим ( dP/dt <  0 ) с точки зрения термодинамики устойчив, второй - име-

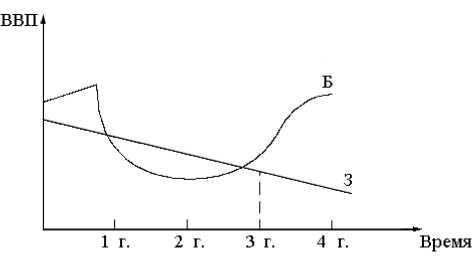
Рис.5. Зависимость ВВП от времени для быстрых (Б) и медленных (З) реформ

первой группы (Польша, Чехия, Словения, Эстония и Латвия).

У стран третьей группы (Россия, Болгария, Украина), проводящих реформирование экономики в режиме инфляционного градуализма, имеет место ухудшение экономической ситуации (падение ВНП, гиперинфляция).