Фрактально-кластерный подход к описанию фундаментальных закономерностей развития биологических организмов

Начиная с развития фрактальной геометрии (Cantor, 1883; Koch, 1904; Hausdorff, 1914; Sierpinsky, 1915; Feigenbaum, 1977; Mandelbrot, 1977), представляющей собой новую ступень познания окружающего мира, понятие «фрактал» проникло практически во все области научных и практических знаний: биологию, химию, математику, астрофизику, экономику, социологию, образование, информатику и т.д.

Обширный обзор исследований по фракталам представлен в монографии (Peitgen et al., 1992), где приведены программные продукты построения фракталов и их иллюстрации. Все новые и новые подтверждения свойств фрак-тальности находят исследователи в различных сферах деятельности (Barsley,1988; Fleishmann et al., 1989). Всесторонние исследования фрактальных свойств и их количественных характеристик для биологических и экологических систем представлены в (Розенберг, 2011; Гелашвили и др., 2013).

Среди всего спектра исследований по данной проблематике особняком стоит исследование Бурдакова В.П. (1997).

В результате многолетних статистических исследований (Бурдаков, 1997) было показано, что в любых самоорганизующихся системах: социальных, биологических системах, прошедших эволюционный путь развития, системах машина-человек всегда имеется пять базовых потребностей, названных кластерами (Бурдаков, 1997). Несомненно, что потребностей у любого организма существенно больше, но их можно упаковать в эти базовые (кластеры) потребности. Это энергетический ( C ₁), транспортный

Волов Вячеслав Теодорович, д.т.н., д.ф-м.н., д.э.н., д.с.н., д.п.н., профессор, заведующий объединенной кафедрой «Естественные науки».

( C ₂), экологический ( C ₃), технологический ( C ₄), и информационный ( C ₅) кластеры, имеющие в условиях нормального функционирования определенные (идеальные) значения, выраженные в процентах или долях целого для экстенсивного параметра системы (масса, время, объем, и т.п.). Для энергетического кластера это значение приблизительно составляет 38%, транспортного – 27%, экологического – 16%, технологического – 13%, информационного – 6%. (рис. 1). Данные соотношения, названные фрактально-кластерными соотношениями (ФКС) представляют собой термодинамический отпечаток хорошо функционирующего организма любой природы. Под «организмом» подразумеваться исключительно самоорганизующиеся системы, в которых можно выделить пять базовых вышеприведенных кластеров (потребностей). Любая сложная система, в которой в рамках данного подхода нельзя выделить пять соответствующих кластеров, не является «организмом».

Каждый из пяти кластеров имеет пять самоподобных подкластеров, например: в энергетическом – энергетическая поддержка самой энергетической системы, энергетическая поддержка транспорта, экологии, технологии, информатики и т.д. И остальные подкластеры соответствующим образом подразделяются на пять подкластеров следующего уровня, т.е. имеет место иерархическая самоподобная структура распределения ресурсов, представляющая собой фрактал (рис. 2).

Для анализа функционирования биологических, технических и антропогенных систем, как правило, достаточно второго или третьего уровня ФКС. Общая сумма ресурса во всей системе за исследуемый промежуток времени остается постоянной величиной. Такая кластеризация (Бурдаков, 1997) позволила производить оценку функционирования сложной системы. Однако,

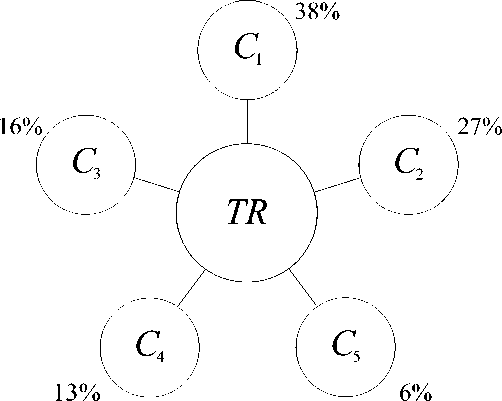
Рис. 1. Фрактально-кластерное структурирование ресурсов организмов по базовым потребностям, TR – общий ресурс организма

a)                         b)

Рис. 2. Иллюстрация фрактально-кластерного структурирования ресурсов «организма» на уровне n =6;

• a) неидеальное распределение ресурсов; b) идеальное распределение ресурсов

  теории или математических моделей на основе ФКС создано не было. Базируясь на инструментарии неравновесной термодинамики в ее информационной интерпретации (Гленсдорф, Пригожин, 1973) и ФКС была разработана фрактально-кластерная теория и ее критериальный аппарат (Volov, 2013), а также проведен анализ механизмов ресурсораспределения в закрытых фрактально-кластерных системах (Volov, Zubarev, 2016). Поэтому целью данной работы было обобщение статистических данных по развитию биологических организмов на основе разработанных фрактально-кластерных критериев (Volov, 2013).

МЕТОДЫ ИССЛЕДОВАНИЯИ ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

В исследовании используется критериальный аппарат фрактально-кластерной (ФК) теории, разработанный в (Volov, 2013), и статистические данные по 39 видам биологических организмов, которые были кластерированы в соответствии с фрактально-кластерными соотношениями (Бурдаков, 1997) (табл. 1).

При анализе были использованы следующие критерии:

• 1)    фрактально-кластерная энтропия H (Volov, 2013), определяющая долю ресурсов организма, идущую на удовлетворение всех его энергетических потребностей, имеет следующий вид:

  h ( n )= c i + У

  i = 2

  
  

( 5     5 _

У ... У c ,

V j 1 = 1      j n - 2 = 1

где n - номер уровня ( n > 2), C 1 = C₁ У C i и

C,     = C.

^ij ! ••• ^jn - 2 ^{1            ij} 1— ^jn - 2 ¹

^Ci .

• 2)    высокочувствительный фрактально-кластерный критерий ресурсораспределения D определяется согласно (Volov, 2013) формулой:

Таблица 1. Матрица идеальных фрактальных-кластерных соотношений

Ci C= 0,38 C, C11 r v 12 13 v 14 C15 0,144 0,1026 0,0608 0,0494 0,0228 0,27 C2 21 22 CL 23 24 25 0,1026 0,0729 0,042 0,0351 0,0162 0,16 C} 31 CL 32 cL 33 34 35 0,0608 0,0256 0,0208 0,0169 0,0078 0,13 C4 41 42 43 44 45 0,0228 0,0351 0,0208 0,0169 0,0078 0,06 C5 C51 52 53 54 C55 0,0228 0,0162 0,0096 0,0078 0,0036 1 C= 0,38 0,27 0,16 0,13 0,06 где

555  5

log5               a ’ ^k- i=1 j=1 k=1 m=1

log₅ N

ideal ²

Для определения фрактально-кластерной вероятности P(D) как функции D -критерия был проведен численный эксперимент по возможным комбинациям кластеров в области их допустимых значений (Volov, 2013):

*

Q..,   = 1 — ijk...m

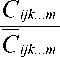
,       ijk...m

– значе-

ния кластеров и подкластеров n -го уровня для идеальной и фактической матрицы отнесенных к суммарному ресурсу системы; N – общее число кластеров и подкластеров структурирования. D -критерий (2) при внешнем сходстве с формулой определения Хаусдорфовой размерности (Peitgen et al., 1992) имеет качественные отличия от последней. Хаусдорфова размерность геометрического пространства может принимать целые и дробные значения, а размерность фрактально-кластерного пространства ( D -критерий), кроме того, может принимать отрицательные значения. При этом значения кластеров, входящих в определение D -критерия (2) подчиняются закону сохранения ресурса организма на определенном интервале времени. На рис. 3 представлено распределение ресурсных состояний ФК-системы в фазовой плоскости ( D -критерий – C ₁). Из рис. 3 видно, что, начиная с определенных отрицательных значений D -критерия D ≤-1,5, возникают необратимые нарушения ре-сурсораспределения ФК-системы.

C min = 0,078, C max a 0,8, min C 2 = 0,063, "74 max C 2 = 0,73, min C 3 = 0,035, z~v max C 3 a 0,7, min C 4 = 0,03, z~v max C 4 a 0,65, C min = 0,02, C max a 0,55, удовлетворяющих аналогу закона сохранения nml q

IZZ - I Cm = 1 .    (3)

i = 1 j = 1 k = 1 z = 1

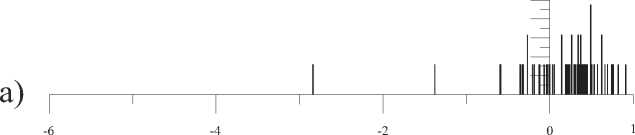
В результате было получено фрактально-кластерное (ФК) распределение возможных ресурсных комбинаций (рис. 4). ФК-вероятность P(D) определяется как отношение ресурсных комбинаций значений кластеров, удовлетворяющих аналогу закона сохранения ресурса (3) к общему числу комбинаций. Локальное натяжение известных распределений на ФК-распределение не привело к позитивному результату, что свидетельствует о новом вероятностном распределении. Аппроксимация данного распределения имеет следующий вид:

D

0.5

0         0.5 С !

Рис. 3. Фазовая плоскость D -критерия ресурсных состояний и энергетического

кластера «организма»

P (D ) =

a + b ■ D + c ■ D² . ( 1 - D ) d h + 1 ■ D + g ■ D ²

( c i ^ exp

)

c 2 )

^

— 1 J

где a =–9,391; b =8,308; c =0,705; f =–5,776; g =3,474; h =2,617; H₀ =0,618; d =4 H₀ ;

1/ ²

о c1=- 0,592; c2 = -7---777.

2 ■ I 1 - H^ I

I 50 J

Предельное значение распределения при n =100 представлено на рис. 4f.

Для оценки максимальной энергии “организма” использовался термодинамический потенциал F , определяемый следующим образом:

F = U - TS ,           (5)

где U – внутренняя энергия системы, T – температура, S - термодинамическая энтропия. Дан-

ный потенциал называется свободной энергией и характеризует максимальную возможную работу, которую может совершить “организм”. Аналогом потенциала F во фрактально-кластерных моделях (Volov, 2013) является свободная фрактально-кластерная энергия “организма”, определяемая следующим выражением:

F = C 1 - H . (6)

ОСНОВНЫЕ РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

На основе статистических данных по биологическим организмам (табл. 2), их кластеризации и использования фрактально-кластерных критериев получены следующие результаты, представленные в табл. 3.

В результате проведенного анализа на основе фрактально-кластерного подхода были выявлены три фундаментальных закономерности для биологических организмов:

• 1)    вероятностная ФК-закономерность определяет вероятность возникновения биологических организмов в зависимости от совершенства распределения ресурсов в организме, определяемого D -критерием. Как видно из рис. 5, имеется биекция – наиболее древние биологические организмы (менее совершенные), например, хламидомонады, гидры и др., имели наибольшую вероятность возникновения P(D) ~0,01;

• 2)    эволюционная ФК-закономерность (рис. 6) иллюстрирует увеличивающуюся сложность и совершенство возникающих организмов во времени, начиная с древнейших организмов и до человека;

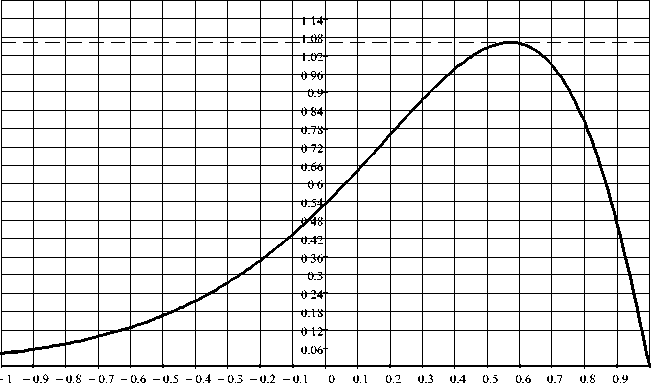
• 3)    энергетическая закономерность (рис. 7) характеризует энергетическое совершенство биологических организмов (зависимость фрактально-кластерной энтропии H или критерия F о нормализованного значения энергопотребления на 1 кг веса организма в сутки).

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Вероятностная закономерность развития биологических организмов получается за счет распределения возможных состояний фрактально-кластерной системы в зависимости от D -критерия и соотнесения данного распределения с обработанными значениями D -критерия для биологических организмов (табл. 2).

Из рис. 5 видно, что фрактально-кластерная вероятность появления человека на Земле имеет вполне ощутимое значение P(D) ≈ 5×10^-4.

Вторая ФК-закономерность показывает рост совершенства распределения ресурсов в организмах ( D -критерий) во времени (рис. 6).

На рис. 7 представлена третья выявленная

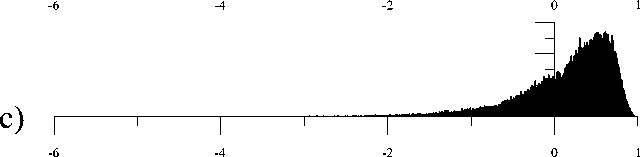
d)

-6

-4

-2

-6                               -4                               -2                               0               1

D

P -10"2

f)                 D

Рис. 4. Распределение фрактально-кластерной вероятности как функции D -критерия. Здесь графики (a), (b), (c), (d), (e) и (f) соответствуют значениям разбиения допустимых интервалов кластеров на 10, 20, 30, 40, 50 и 100 равных частей

ФК-закономерность, определяющая связь свободной фрактально-кластерной энергии биологических организмов и уровнем энергопотребления на 1 кг веса. Данная закономерность представляет собой в определенном смысле энергетический ответ на проблему «маятника» Лотки-Вольтерры («хищник-жертва»): судя по уровню свободной фрактально-кластерной

Таблица 2. Фрактально-кластерные соотношения масс биологических организмов (самцы)

Название организма Масса, кг ФКС, % Э (С1) Тр (С2) Эк (Сз) Тех (С4) И (С5) Chlamydomonas 3-10"11 40±10 10±8 30±6 10±5 10±5 Hydra vulgaris 10-5 40±10 30±8 10±6 10±5 10±5 Micromys minutus 5-10-3 40±6 27±5 16±4 10±3 7±2 Agrionemys horsfieldi 0,1 38±6 20±5 30±4 7±3 5±1 Larus argentatus 1,0 39±6 28±5 16±4 10±3 7±2 Lepus timidus 5,0 40±6 28±5 16±4 11±3 5±2 Castor fiber 30 40±6 26±5 17±5 12±3 5±2 Pan Oken 60 39±6 28±5 16±3 11±2 6±2 Homo Sapiens 68 38±6 27±5 16±4 13±2 6±1 Gorilla 250 39±6 28±5 16±3 11±2 6±1 Galeocerdo cuvier 500 40±6 30±5 16±4 8±3 6±2 Hippopotamus amphibious 3000 40±6 28±5 16±4 10±3 6±2 Loxodonta africana 5000 40±6 28±5 16±4 10±3 6±2 Balaena mysticetus 1,5-105 42±5 28±4 16±3 8±2 6±1 Balaenoptera musculus 2-105 42±5 28±4 16±3 8±2 6±1 энергии (F) у биологических организмов (включая млекопитающих, рыб, насекомых и т.д., за исключением червей – крайние правые точки на рис. 7) – имеется в среднем энергетический баланс между «хищниками» и их «жертвами» – «хищник» не может догнать свою «жертву». Полученная энергетическая закономерность для биологических организмов (рис. 7) является термодинамическим подтверждением решения проблемы – «хищник-жертва»: «хищники» не могут уничтожить всех потенциальных «жертв» (рис. 8), т.е. гибнут только особи, имеющие уровень свободной энергии ниже среднего по популяции.

Важно отметить, что математическое выражение для второй и третьей закономерности имеет один и тот же вид:

X

Z(x) = a --,              (7)

где a , β , α - константы.

Выражение (7) для эволюционной ФК- закономерности имеет вид:

D = 1

_т ^{0, 275}

H ₀ - io ³

где H ₀=0,618 – энтропия «золотого сечения».

Энергетическая фрактально-кластерная закономерность запишется следующим образом:

E ^{3 H} o

1F l=7 - H^ ,    (9)

где γ =0,24. В выражении (9) свободная фрактально-кластерная энергия берется по абсолютной величине, так как свободная энергия в физике определяется термодинамическим потенциалом Гельмгольца, имеющим отрицательное значение.

ЗАКЛЮЧЕНИЕ

Проведенный критериальный анализ 39 видов биологических организмов позволил выявить три фундаментальные закономерности: 1) вероятностную; 2) эволюционную; 3) энергетическую. Вероятностная закономерность связывает термодинамическое совершенство организма ( D -критерий) с фрактально-кластерной вероятностью и с временем возникновения биологического вида: менее совершенные организмы ( D -критерий меньше) имели большую вероятность их возникновения. Эволюционная закономерность связывает термодинамическое совершенство организма с временем его возникновения. Энергетическая закономерность представляет собой термодинамический ответ на проблему «маятника» Лотки-Вольтерры –

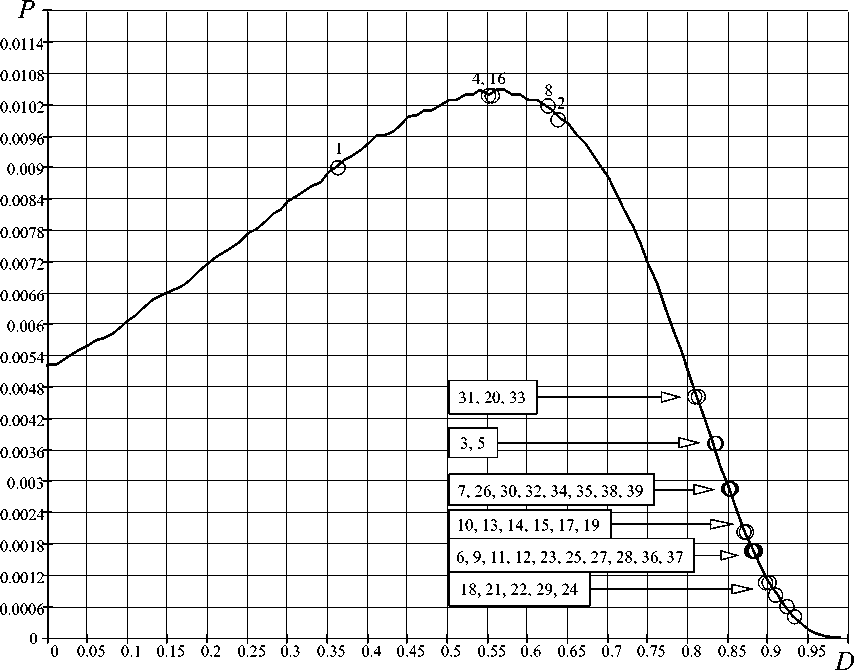
Рис 5. Вероятностная ФК-закономерность возникновения биологических организмов.

Нумерация на рисунке соответствует порядковым номерам биологических организмов (Табл. 3)

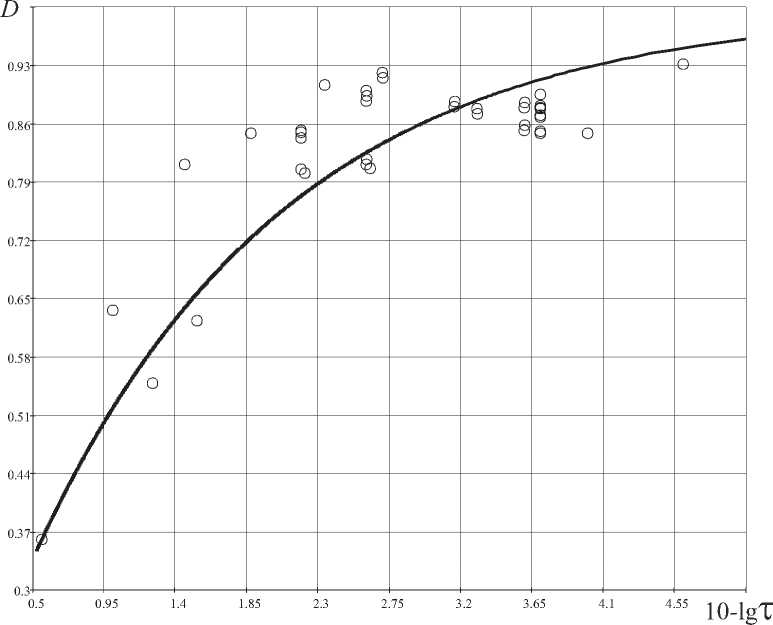
Рис. 6. Эволюционная ФК-закономерность для биологических организмов, τ – время, направленное в прошлое, ° – значения D -критерия для организмов (Табл. 3)

Таблица 3

	Species of Biological organism	D	H	C 1	F
1	Chlamydomonas	0,361	0,622	0,387	-0,235
2	Hydra vulgaris	0,636	0,637	0,4	-0,237
3	Scorpiones mingrelicus	0,833	0,561	0,338	-0,223
4	Oligochaeta	0,549	0,342	0,19	-0,152
5	Anisoptera libellula depressa	0,832	0,832	0,4	-0,238
6	Micromys minitus	0,882	0,639	0,4	-0,239
7	Rona ridibunda	0,849	0,639	0,4	-0,239
8	Testudo horsefieldi	0,624	0,614	0,38	-0,234
9	Cucules canorus	0,882	0,639	0,4	-0,239
10	Procellariida	0,872	0,662	0,42	-0,242
11	Larus argentatus	0,883	0,627	0,39	-0,237
12	Heroestes edwardsi	0,879	0,639	0,4	-0,239
13	Ciconia ciconia	0,868	0,664	0,421	-0,243
14	Lepus timidus	0,871	0,639	0,4	-0,239
15	Grus grus	0,868	0,664	0,421	-0,243
16	Paralithodes camtchatica	0,553	0,359	0,2	-0,159
17	Pelecanida onocrotalus	0,871	0,639	0,4	-0,239
18	Vulpes	0,895	0,639	0,4	-0,239
19	Castor fiber	0,868	0,664	0,421	-0,243
20	Acinonyx jubatus	0,811	0,639	0,4	-0,239
21	Canis lipus	0,9	0,639	0,4	-0,239
22	Pan troglodytes	0,907	0,627	0,39	-0,237
23	Orycturopus afer	0,881	0,633	0,395	-0,238
24	Homo sapiens	0,932	0,614	0,38	-0,234
25	Ursus arctos	0,879	0,639	0,4	-0,239
26	Cervina nippon	0,852	0,639	0,4	-0,239
27	Sus scrofa	0,878	0,639	0,4	-0,239
28	Pongo pygmaeus	0,883	0,627	0,39	-0,237
29	Gorilla gorilla	0,922	0,627	0,39	-0,237
30	Equida burchelli	0,849	0,636	0,4	-0,239
31	Tursiops	0,806	0,659	0,42	-0,242
32	Equus caballus	0,849	0,636	0,4	-0,239
33	Galeocerdo cuvieri	0,811	0,639	0,4	-0,239
34	Camelus bactrianus	0,851	0,639	0,4	-0,239
35	Giraffa cameleopardalis	0,852	0,639	0,4	-0,239
36	Hippopotamus amphibius	0,878	0,639	0,4	-0,239
37	Loxodonta africana	0,878	0,639	0,4	-0,239
38	Balaena mysticetus	0,849	0,663	0,42	-0,243
39	Balaenoptera musculus	0,849	0,663	0,42	-0,243

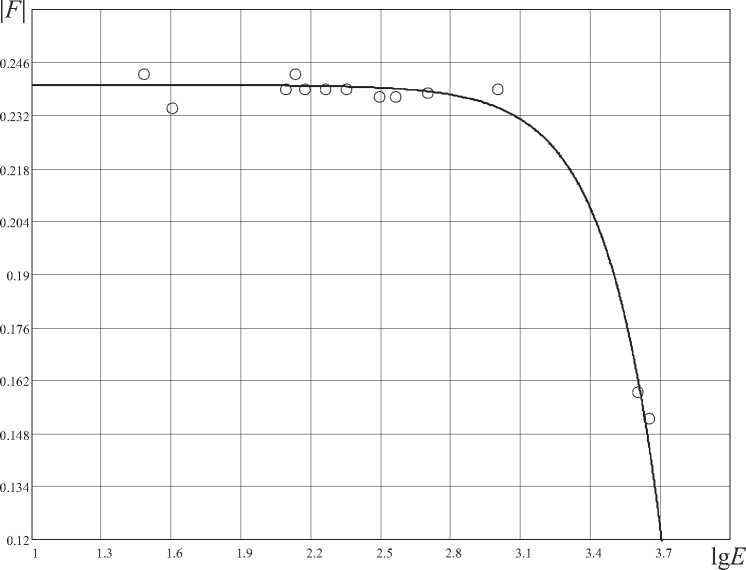
Рис. 7. Энергетическая ФК-закономерность для биологических организмов

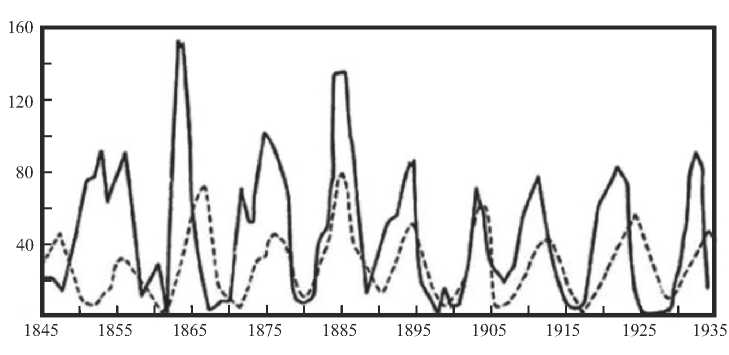
Рис. 8. Динамика популяции рысей и зайцев (сплошная линия – популяция зайцев, штрихованная линия – популяция рысей)

«хищник-жертва». Популяция «хищников», так же, как и популяция «жертв», не может полностью исчезнуть, поскольку в среднем их свободная фрактально-кластерная энергия имеет одно и тоже значение, т.е. «хищник» не может догнать «жертву» - гибнут «жертвы», имеющие свободную фрактально-кластерную ниже среднего уровня по популяции. Обобщая выше сказанное можно констатировать, что «маятник» Лотки-Вольтерры является динамическим энергетическим условием невозможности уничтожения «хищниками» своих потенциальных «жертв», а полученная оценка на основе критерия свободной фрактально-кластерной энергии популяции «хищников» и их «жертв» - статическим энергетическим условием.