Фрактальное описание фазовых переходов в конденсированных средах

Изучение физико-химических свойств материальных тел с помощью континуальных моделей предполагает наличие непрерывных пространств, геометрия которых формируется исследуемой средой и может быть евклидовой, римановой или фрактальной.

Природа на всех её масштабах от кварков и генов до галактик и их скоплений наполнена «неправильными», изломанными, так называемыми фрактальными формами, которые в математике описываются непрерывными недифференцируемыми функциями. Это контуры берегов озер, рек и морей, формы облаков, рельефы различных поверхностей, кровеносные, нервные и дыхательные системы, структура тканей живой плоти и т. д. В целом, как писал основатель фрактальной геометрии Б. Мандельброт, «... у геометрии природы фрактальное лицо» [1].

Пространственная размерность фрактальных структур, как правило, дробная. Кроме того, они обладают свойством самоподобия, то есть их части подобны целому, и они выглядят одинаково, вне зависимости от того, в каком масштабе ведётся наблюдение. Следует отметить, что последнее условие в строгом смысле выполняется лишь для математических множеств, моделирующих те или иные природные объекты.

В конденсированных средах фракталь-ность возникает не только потому, что матрица или каркас структуры могут являться фрактальными, но таковым может быть и обратное (спектральное) пространство — вследствие анизотропии ковалентных, ионковалентных, металлических и других типов химической связи между различными атомными слоями или цепочками. Невозможность строгого учёта указанных обстоятельств в рамках евклидова пространства долгое время ограничивала область применимости континуальных моделей (например, теории Дебая) узким классом тел с простым строением кристаллической решётки. В общем случае, как показано в [2–5], структуру фононного спектра следует представлять в фрактальной форме, после чего континуальные модели становятся пригодными для материалов сложного химического состава, в том числе для различных наноматериалов, а также, как показано в настоящей работе, и для исследования фазовых переходов.

В случае, когда существенны ограничения по размерам образца (например, в наноматериалах), необходимо проводить «обрезание фононного спектра снизу». В этом случае выражение для плотности фононного спектра g ( ω ) имеет вид [5]:

g ^{( ш} ) =

3 Nd f ш ^ - ¹

d f         d f

ω max - ω _min

где N — число атомов; d f — показатель размерности фононного спектра; ω max , ω min — частоты, соответствующие его границам (верхняя и нижняя соответственно).

В связи с влиянием размера нанообъекта на нижнюю границу его фононного спектра наименьшей частоте колебаний ш min целесообразно поставить в соответствие температуру 9n = ^шmin/kB независимо от того, является объект фрактальным или нет [6]. Таким об- разом, физико-химические характеристики нанообъектов, в отличие от бесконечных по спектру длин волн образцов, зависят от двух характерных температур - OH = h ш max/kB и ON — температуры, соответствующей наибольшей длине волны колебаний λmax = 2πv/ωmin в образце.

Введение фрактальной размерности d f существенным образом расширяет возможности моделирования реальных фононных спектров твёрдых тел по сравнению с теорией Дебая (рис. 1) и обеспечивает возможность исследования материалов с низкочастотной расходимостью фононного спектра ( d f <  1). К подобным объектам могут относиться, например, рыхлые фрактальные структуры [7].

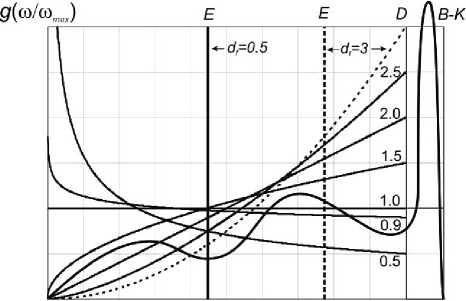
0 0.1 0.2 #3 0.4 0.5 0.6 0.7 0.8 0.9   1

to/®™

Рис. 1. Частотные зависимости фононного спектра g ( ω/ω max ) при ω min =0для структур различной размерности d f . Обозначения E , D и B — K указывают на спектры эйнштейновской, дебаевской и борн-кармановской модели соответственно

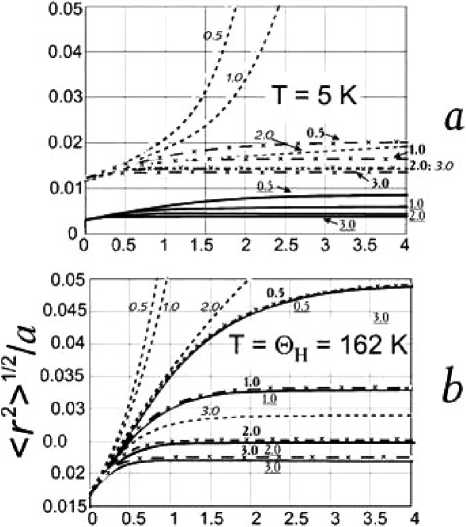
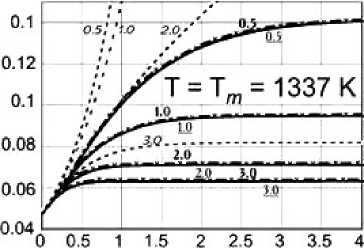
На рис. 2 для различных температур (рис. 2 a — T =5К, b — T = θ H = 162 Ки c — при температуре плавления T = T m = 1337 К) приведены результаты расчётов относительного среднеквадратичного смещения ² >  ^{1 / 2} /a атома Au в зависимости от масштабного параметра lg ( O H /O N ) ^ 1g ( L/a ), где L/a — отношение линейных размеров тела к среднему межатомному расстоянию (пунктирные линии). При этом использовано выражение для температурной зависимости среднего квадрата ² >  атомных смещений при произвольных значениях d f и θ H /θ N , нормированное на один атом [8]:

r ² =

3h ² d f T d f - ¹

Mk B θ _H ^{d f}

^^^^^^^^^r

----7" X _{θ N} d f

x max

^X I (2 ^— e x — i) x ^f - ²■    ⁽²⁾

x min

Здесь x = hш/к в T , x max = O h /T , x _min = θ _N /T , M — масса атома (в расчётах принимались значения M = 327 • 10 t ²⁷ kg , a =0. 408 нм, θ H = 162 К (золото).

ig(V0w)

Рис. 2. Рассчитанная зависимость отно- сительного среднеквадратичного смещения  1/2/aот lg(θH /θN ) для Au при различных температурах: а) T =5К; b) T = θH = 162 К; c) T = Tm = 1337 К. Пунктирными кривыми представлена дебаевская модель, штрих-пунктир — модель Эйнштейна, сплошные линии — классическая модель колебательных смещений. Цифрами 0,5, 1,0, 2,0 и 3,0 обозначены соответствующие значения параметра df

Полученные данные свидетельствуют о том, что для твердотельных структур, осреднённый фононный спектр которых описывается дебаевским законом (df =3), модель бесконечного по спектру длин волн образца пригодна вплоть до наномасштаба, независимо от температуры T . Однако при df ^ 2 она становится неприменимой, и соответствующее относительное смещение  1/2/a уже зависит от L (или отношения θH /θN). Возникает низкочастотная расходимость фононного спектра или «инфракрасная катастрофа» — своеобразный аналог «ультрафиолетовой катастрофы» в теории излучения. Для функции (1), если шmin = 0, эта расходимость имеет место при df < 1, для функции (2) — при df < 2.

В связи с этим целесообразно обратиться к эйнштейновскому представлению величины ² >  при произвольных значениях d f . В этом приближении все квантовые осцилляторы колеблются с некоторой характерной частотой <ω> . Поэтому вместо соотношения (2) будем иметь

(г ² )   ³ [^М +

'  M 2

h (ш)            1

+

exp (h (ш) /к в T ) - 1J (ш} ² ’

где (ш) — эйнштейновская частота, определённая как средняя по всему спектру:

Таким образом, вопрос о роли, которую играют в физике твёрдого тела континуальные модели Эйнштейна и Дебая, приобретает новые аспекты. Если в теории теплоёмкости приоритет модели Дебая не вызывает сомнений, то в задаче о динамике колебаний решётки он далеко не очевиден. Известно, что в мёссбауэровской спектроскопии при анализе температурной зависимости фактора Дебая–Валлера модель Дебая даёт другое, по сравнению с теорией теплоёмкости, значение характеристической (дебаевской) температуры θ _H. Вероятно, это связано с изменением частотной зависимости подынтегральной функции в (2), которая при d f <  2 ведёт к расходимости («инфракрасная катастрофа»).

Известно, что твёрдые тела при определённых условиях могут переходить из одной аллотропной модификации в другую, а при интенсивном нагревании — в стадию плавления. При этом средний квадрат колебательного смещения атома достигает некоторого критического значения < r ^ >  = ( Ya ) ² , где Y ~ 0.1 (критерий Линдемана). Общее выражение для γ можно получить из соотношения (2) при T ^ O H в пренебрежении нулевыми колебаниями. Для произвольных значений d f , θ _H и θ _N оно имеет следующий вид [8]:

^(ш) =

3 N

ω max

шд ( ш ) dш =

₌ (    3h ² d f т _т

^Y   \Мк _в O H a ² ( d f - 2) ^X

ωmin f 1 - ^)df+1 df + 1 max i _( on A df

1 W

Зависимость (4) можно использовать также в случае классического осциллятора, для которого

2 ₌

3 кв T m ш 2'

На рис. 2 представлены результаты расчётов <  ² >  ^{1 / 2} /a для золота по соотношениям (3) — (5). Видно, что в этом приближении расходимость отсутствует, и независимо от размерности фононного спектра d f наблюдается характерная «полка» для зависимости <  ² >  ^{1 / 2} /a от ( θ H /θ N ).

1 — (On/Oh ) df 2 |iI/2 [1 - (On/Oh)df] J где Tm — температура плавления.

При использовании модели (3) — (5) выражение (6) изменяется

(r ² )¹ / ² = ( d f + 1) hy/3 T m /к в M _X a             d f θ H a

[ 1 - ( O n /O h ) df]

^{X [} 1 - ( O n /O h ) ^{d f +1}

В отличие от моделей Дебая и Эйнштейна, с помощью фрактальных континуальных моделей можно анализировать явления, связанные со скачками производных термодинамических потенциалов, то есть фазовые переходы. Формально это связано с тем, что фрактальные модели — многопараметрические, и значения описываемых ими функций, например, температурных изменений теплоёмкости, фактора Дебая–Валлера и др., могут заполнять всё пространство соответствующих термодинамических переменных.

Так, например, при нагревании наночастиц Eu ₂ O ₃ в порах селикагеля было экспериментально обнаружено резкое температурное изменение фактора Дебая–Вал-лера 2 W в случае, когда вместе с Eu 2 O 3 в порах формировались частицы окисла Fe 2 O 3 , задерживающие рост кластеров Eu ₂ O ₃ [9]. Соответствующее аномальное падение вероятности эффекта Мёссбауэра f / = et 2 W свидетельствует о возможности фазового перехода, в частности, плавления. Экспериментальные данные работы [9] по температурному изменению f ' (или 2W = 4 п ² < r ² > / 3 А ² , где А — длина волны мёссбауэровского кванта) были пересчитаны на зависимость ² >  ^{1 / 2} /a от T и представлены на рис. 3.

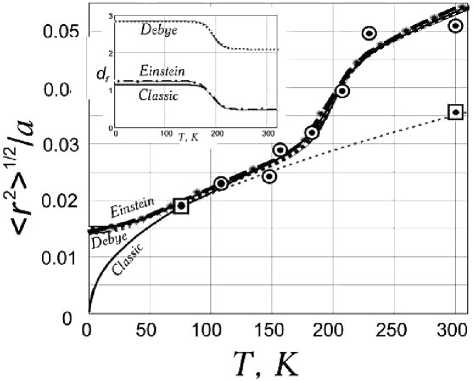
Рис. 3. Зависимость относительного среднеквадратичного смещения < r ² >  ¹ / ² /а от lg( 6 h /6 n ) для разных моделей: кривая « -· -· - » — модель Эйнштейна; пунктирные кривые « --- » — модель Дебая; « - » — классическая модель. Экспериментальные точки — данные из работы [9]

Пунктирная кривая, проходящая через две экспериментальные точки (отмечены прямоугольниками), соответствует образцу, содержащему в порах только массивные частицы Еи ₂ 0 з ( 9 n = 0 К) и удовлетворяет дебаевскому приближению ( d f = 3) с расчётным значением 9 H = 190 К [9]. Используя данные [10]

о температуре плавления T m = 2340 К такого образца при значении критерия Y = 0. 1 из (6), можно получить усреднённое значение межатомного расстояния a = 0 , 44 нм. Далее по соотношениям (2)–(7) можно построить параметрическое семейство функций при различных значениях d f и фиксированной величине отношения 9 _H /9 N ^ L/a = 10, устанавливающего размер частиц L = 4 , 4 нм. Наличие именно таких частиц окисла Eu 2 O 3 в порах материала, содержащего также крупные частицы Fe ₂ O ₃ окисла, следует из результатов эксперимента [9]. Коридор размерностей, в который «укладываются» экспериментальные данные для различных моделей (2-6), показан на вставке к рис. 3.

Расчёты показывают, что область плавления частиц Eu ₂ O ₃ ( y ~ 0 , 1) находится при температурах T m ~ 900 К и лежит за пределами температурного диапазона экспериментального измерения f' (80 ^ T ^ 300 К). Отметим также, что наблюдаемое аномальное изменение f ' может быть следствием аллотропных превращений вещества и уже затем плавлением.

Расчётная методика описания фазовых переходов может быть дополнена использованием дискретных комбинаций выражений для ² > , каждое из которых имеет своё значение d f , или с помощью введения соответствующей функции распределения f ( d f ., T ) — модулирующей зависимости (2)–(6) с мультифрактальным спектром в непрерывном пределе. Весовой вклад компонентов такого спектра или вид соответствующей функции распределения можно определить из МНК-аппрок-симации экспериментальных данных температурной зависимости f ' , < r ² >  и т. п. Пример такого расчёта приведён на рис. 3. Сплошная кривая представляет результат моделирования мультифрактального фазового перехода в модели Дебая и Эйнштейна с использованием модулирующей функции больцмановского типа:

d +__ d f 1 ~ d f 2

f2   1 + exp[(T ~ Tt) D], где df 1 и df2 — показатели размерности фононного спектра до и после фазового перехода соответственно; Tt — температура

∂d f ( T )

перехода; D ∼ _∂ ^f _T — параметр, определяющий его крутизну.

В целом, результаты данной работы показывают то, что фрактальные континуальные модели дают принципиальную возможность исследовать фазовые переходы различной физической природы, связанные с изменением структуры фононного спектра вещества. При этом температурные зависимости термодинамических функций в фазовых переходах при различных d f с помощью данного подхода также могут быть получены.