Фрактальность трафика и очереди в системах массового обслуживания

Измерения на реальных компьютерных сетях и измерения потоков в пакетных сетях передачи данных показали, что передаваемый в них трафик является самоподобным случайным процессом. Для такого трафика анализ очередей на основе традиционных методов теории массового обслуживания пуассоновских потоков становится непригодным [1-9]. Анализу самоподобных процессов телетрафика посвящены публикации [2-3] и др. На качественном уровне самоподобие проявляется в том, что имеется медленно убывающая зависимость между величинами трафика в разные моменты времени, а трафик носит пачечный характер. Эти пачки выглядят статистически подобными в различных масштабах интервалов времени.

Одной из фундаментальных отечественных работ в указанном направлении является монография [2], определения которой мы рассмотрим применительно к анализируемому нами случайному п роцессу. Рассматриваемый процесс является стационарным и дискретным по времени которое необходимо для о бработки одной заявки . Напомним, что и ----------2

– математическое ожидание и дисперсия чисел заявок, поступающих в течение интервала времени соответственно. Обозначим через        элемент, сдвинутый на k интервалов по отношению к Значение корреляционной функции (ковариационный ко- эффициент), при сдвиге на k интервалов обозначим через

Мт (к; Г) = [т,.(г) - т(т№,__к (г) - w(r)].

Очевидно, что дисперсия                – это ковариационный коэффициент при нулевом сдвиге        Нормированная корреляционная функция:

(1) ^Dm^

Определим объединенный (агрегированный) процесс как

S i=slJ-YH\ то есть процесс разбивается на непересекающие-ся интервалы времени размером значения на каждом интервале усредняются, а j используется для нумерации полученных агрегированных интервалов. Обозначим математическое ожидание агрегированного процесса         через а дисперсию агрегированного процесса

– через         Очевидно, что m{s} (r) =—Уm|s).(r) =

=           S '»,(Z") = »7(Z-) • sNs ./=1 ,=,(./-i)+i

Обозначим корреляционную функцию агрегированного процесса m^w ^т) через ^"„Лк;^, а нормированную корреляционную функцию – через

В соответствии с принятыми определениями, статистический процесс nW) называется строго самоподобным с параметром самоподобия H , где 0,5<Я<1, если для всех 5 > 1 процесс s^x~^H rW jYc) имеет те же статистические характеристики второго порядка, что и »WX то есть выполняются соотношения

W^WW^DWY rWWW^WW-

для любых s > 1, то есть его нормированная корреляционная функция должна обладать масштабной инвариантностью. Такой масштабной инвариантностью обладает корреляционная функция:

r_m (к- г) = <„ (к; г) = [( к + 1Г - W” + (к - 1)^2Я ]. (4)

Процесс с указанной корреляционной функцией демонстрирует долговременную зависимость, если коэффициент H, называемый параметром Херста [2], удовлетворяет условию 0,5<Я<1.В этом случае limr (£;г) Нт/' (к;т)            ,          ...

_rWn =--р^^^{С при} ^^°°’ (5)

где 1 = 2(1 -Я) – коэффициент, меняющийся в пределах О < ^ < 1, а C – некоторая медленно меняющаяся функция. Нетрудно показать, что при отсутствии корреляции, Я = 0,5 и нормированная корреляционная функция убывает пропорционально первой степени увеличения коэффициента сдвига k .

Для самоподобных процессов убывание корреляционной функции происходит намного медленнее. Поскольку, в соответствии с (1) М,„(к;т) является корреляционной функцией центрированного процесса, значения медленно меняющейся функции близки к нулю. Таким образом, самоподобные свойства отражают влияние масштабирования процесса во времени (агрегация) на значения вероятностных характеристик процесса, в то время, как автокорреляционная функция отражает наличие долговременной зависимости. В общем случае из наличия самоподобных свойств не вытекает свойство долговременной зависимости, и наоборот.

Если выполняется соотношение 0,5<Я<1,то самоподобный процесс обладает также свойством долговременной зависимости. Из (5) следует, что величина ^г„.(к;^ убывает по степенному закону. Это означает, что корреляционная функция является не суммируемой, и ряд, образованный ее последовательными значениями, расходится:

^гт(к;т) = со.

Образование очередей

Будем считать, что случайная величина, образующая самоподобный процесс, центрируется, и нет никаких ограничений на значение ее математического ожидания. В действительности реальная случайная величина 11ф\ представляющая числа заявок, поступающих в течение интервалов обслуживания одно й заявк и, имеет математическое ожидание m.(r) = 5_i(T) = р<1, где р – коэффициент загрузки СМО. Для любой одноприборной СМО справедливо рекуррентное соотношение, устанавливающее связь между поступающими и обработанными заявками [4].

q^^cp^^m^-SXTY,       (7)

5^^

О, если q_i-x (г) = m_t (г) = 0 ;

1 в противном случае.

На рисунке 1 а показаны пачки заявок, поступающие в течение последовательных интервалов времени г, равных интервалу обслуживания одной заявки. На рисунке 1 b показаны соответствующие значения переменной 5^т\ На рисунке 1 с показан процесс образования очередей д^т\

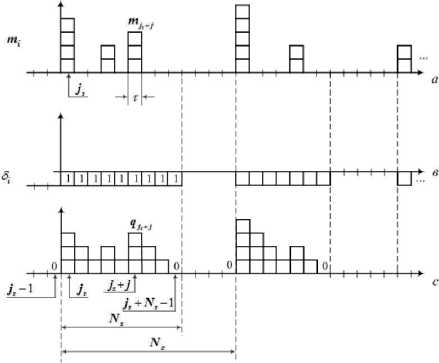
Рисунок 1. Формирование очередей

Процесс образования очередей носит циклический характер. Каждый цикл N_c состоит из двух периодов: период обработки N_u (период активной работы процессора, когда <>» = !) и период простоя N_p (период, когда заявки в системе отсутствуют и ЗАП-ОУ Кроме того, выделим цикл очередей, включающий ^s интервалов, расположенных на периоде занятости между двумя интервалами, на которых очередь 9,(r) принимает нулевые значения. Рассмотрим очереди на отдельном цикле очередей Д ’ который начинается на интервале z = j_s и заканчивается на интервале i = j_s+N_s-\, на котором значение очереди равно нулю. На интервале i = Л -¹ очередь q_JS-M также отсутствует. Поскольку величина S^r) может принимать только единичные или нулевые значения, на интервалах, где 5(r) = 0 , заявки и очереди в системе полностью отсутствуют.

Средние значения очередей

Для получения средних значений очередей возведем обе части уравнения (7) в квадрат:

q\ (r) = q\__x (r) + 2^_! ДЖ (г) - 8₍ (г)] + [m,. (г) - 8, (г)]².

Учитывая, что З2 (г) = 8; (г); 8, (т)т^ = ni; (г); 8^ = т^; 8^^ = ^(г), проанализируем выражение Ж^Н2")-^2")]- Если д^М^О, то 5Ar) = l. Если ^,-i(r) = O, то результат не завит от З^т), и вместо бАй может быть подставлена любая величина. Будем считать, что указанная величина равна единице. Тогда, при заданных ограничениях, выполняется равенство q2,^) = q2i-i(^ + ^qi-i^XmjU) -1] + т\(г) - m, (т).

Учитывая, что 777,. (г) = А г = p , после усред нения п олучим т\ (г) - 777,. (г) = Д„ (р) + р(1 - р); 9²,(2-) = д²,_₁(г).

Проанализируем соотношение

4i-x (0['«,(г) -1] =           (^г)[^/и, М ~ Ч • (9)

Разобьем интервал N на подынтервалы, каждый из которых соответствует одному полному циклу. Учитывая, что на всех пассивных участках циклов qiW = o, получим

________________________ 1 М j.,+N,

Чх.хи^тДт)-!^—^ ^ ^(г)^/^^-!].

Далее проанализируем изменение q^) в пределах одного цикла Zs. Поскольку активный период цикла Zs начинается с интер- вала j , на предыдущем интервале очередь отсутствует и ^_i(r) = O. На последнем интервале Л+^-1 активного периодаqj.NAr> = 0 . На всех интервалах активного периода 8^ = Vjej Aj +W -1), В [6] было показано что

⁹^⁼^7F 2L У.К^-т_мД (10) '          Z₅c[1,jV] ./=0

Из (10) следует, что значения очередей определяются независимо внутри каждого цикла.

Заключение

Таким образом, с целью анализа очередей, создаваемых в СМО самоподобными процессами, необходимо учитывать, что математическое ожидание случайной величины 777,. (r) всегда меньше единицы, а корреляционные свойства процесса, с точки зрения образования очередей, определяются не знач ениями центрированной переменной77?,.(r) — 777(r), а значениями разностной переменной [777, (r)- 8, (г)], которая может удовлетворять свойствам самоподобия, но долговременная корреляционная зависимость тДт") компенсируется корреляционной зависимостью величины 5j (т )• Процесс, образуемый указанной переменной, имеет временные интервалы, на которых ^(r^O, прерывающие зависимость очередей на различных циклах. Следовательно, ни о какой долговременной зависимости очередей здесь говорить не приходится, она компенсируется. Это еще раз подтверждает, что самоподобный трафик, имеющий долговременную корреляционную зависимость, при обработке в СМО долговременную зависимость очередей теряет, и соотношение (6) не выполняется. При этом сумма

^ги_д.(Дт) = С, есть не бесконечная, а некоторая конечная медленно меняющаяся функция. На свойства разностной величины [777,(r)- 8; (r)] обращал внимание еще автор [1], полагая, что именно эта случайная величина определяет характер очередей в СМО.