Фрактальные свойства разрушающих программ

Растущая мощность множества угроз программным средствам, как наиболее уязвимым элементам информационных систем, актуализирует задачи предотвращения несанкционированного и нелегитимного доступов. Современные контрольно-испытательные методы и методы сигнатурного анализа безопасности не всегда могут гарантированно, с достаточной степенью достоверности обнаружить постоянно совершенствующиеся программные разрушающие средства (ПРС). Попытки повысить достоверность за счет анализа статистических свойств структурных элементов программ [1-2] не всегда дают положительный результат из-за неадекватности гипотез относительно свойств статистик. В связи с этим здесь изучаются возможности применения фрактального анализа. Изучение опирается на гипотезу Ципфа о равновесной структуре языка [3], обусловленной, как он полагал, компромиссом двух противоположных тенденций: стремлениями к меньшим усилиям (потратить меньше слов) и к большей активности (текстового разнообразия).

При статистическом исследовании текстов и их элементов (слогов, фонем, иероглифов и т.п.) практически любого языка Ципф наблюдал степенную зависимость между частотой встречаемости элементов и рангом (местом элемента в ряду в порядке уменьшения частоты). Получающийся при этом фрактал со своей размерностью может служить индикатором наличия программного разрушающегося средства, т.к. естественно ожидать отличия фрактальных размерностей у множеств элементов программного продукта, не имеющего закладок, и ПРС. Проверка справедливости такой гипотезы достаточно важна, так как проблема разрешимости множества программных разрушающих средств не решена. Ниже обосновывается частотная и ранговая фрактальные модели, описывающие свойства языковых конструкций программных продуктов, включая и зараженные.

• 2.    Фрактальные свойства кинетических моделей после преобразований методом С. Ли

Предполагается, что системное поведение основных программных конструкций типа операторов, операндов, их множеств может быть модельно интерпретировано как кинетический процесс. В таком контексте рассматривается уравнение Фоккера–Планка–Колмогорова или диффузии в дивергентной форме, к которой можно преобразовать общую форму кинетического уравнения в значительном числе задач практики. В одномерном случае дивергентная форма кинетического уравнения для относительного числа f = f ₁ =x X включений операторов языка (слов текста) в программу записывается в виде:

df/St = 0,552 (B1 f) / SI2.            (1)

Форма (1) получается при условии выполнения равенства 0,5 ( dB 1 /QI ) = A 1 , являющегося следствием принципа детального равновесия. Частным видом кинетического уравнения (1), используемого в моделях диффузии, характеризующимся независимым от аргумента I коэффициентом диффузии B 1 = 2D, является:

df/St = Dd ² f/ dI ² .            (2)

Аффинные преобразования, примененные к уравнению (2), приводят его к форме обыкновенного дифференциального уравнения, имеющего автомодельные решения. Для нахождения последнего используется метод построения базиса алгебры Софуса Ли [4], допускаемой дифференциальным уравнением, и извлечения инфинитезимального оператора аффинного преобразования из операторов базиса. В результате получается инвариант аффинного преобразования ^ = 12t-1, который, действуя в пространстве независимых переменных исходного кинетического уравнения, принимается за новую независимую переменную. Ее подстановка в исходное кинетическое уравнение преобразует последнее в обыкновенное дифференциальное уравнение вида:

dfi =cifibi, dξ d-1

b=,c

2d1 - 1 2

cd⎞ ^d 1 ^{- 1} k^⎟⎠     ^,

d ₁

∂2f

∂ξ2

∂f

+α =0,α

∂ξ

⎛1+1⎞

⎜⎝ξ 4D ⎟⎠

d ⎛1 b1=b21 ,c1=⎜d⋅cd ⋅k d⎜

^- d ₁

,b _i > 0,i: = 1,2.

Асимптотика коэффициента α при фиксированном времени t и I →∞ приводит к константе а = ( 4 D ) ^{- 1} .

Уравнение типа (3) можно записать как в пространстве переменной I = x (числа включений оператора языка (слов текста) в программу) – для f 1 , так и в пространстве I = n ( x ) (числа операторов языка программирования или Ассемблера, кластеров системы, использующихся в программе x раз) – для f ₂ . При этом получается система двух обыкновенных дифференциальных уравнений:

Итак, два классических уравнения диффузии в дивергентной форме имеют фрактал в пространстве производных от искомых функций f ₁ и f ₂ по инварианту ξ . Кроме того, эти уравнения могут иметь фракталы в пространстве искомых функций f ₁ и f ₂ . Можно показать, что в этом случае их решения f ₁ и f ₂ находятся в виде:

. f = [к^ + k 2, (^ - ^ 0)] 1-bi,            (8)

где b; >0,k = f 0,(1"b'),k = c, (1 -b,),

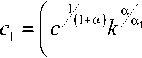
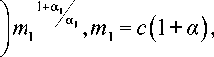
∂ ² f 1 ∂ξ ²

∂f

=-α 1.

i _{∂ ξ}

Здесь a i = ( 4 D i ) ^{- 1}. Делая аналогичные [5] преобразования, несложно получить на основе (4) фрактал в пространстве первых производных

по инварианту ξ:

∂f1=k ∂ξ

⎛∂f2

⎜⎝∂ξ

d ₁

c ₂ = m 1 a 1 ,m = ( 1 + a ) ck, i : = 1,2.

Простой проверкой можно убедиться, что линейная модель в пространстве инварианта ξ получается из полученных выше уравнений при d i = d (здесь индексы (1, 2) для краткости опущены). Действительно, именно при таком условии уравнения ФПК преобразовываются к линейному виду:

где dx = sa1/а2 £ = I2t-1 ,s = ^ /^ ,£, =^ .

Очевидно, такой фрактал характерен для всех уравнений ФПК класса (2) при выполнении условия ∂f ₂ ∂ξ>0 . Кроме того, в правой части (4) более точное выражение для коэффициентов a i = ( 4 D i ) 1 должно быть записано в виде (3). Потому и фрактальную размерность правильнее записать более строго. Но, учитывая, что при изменении в рабочей области аргумента ξ ln ξ величина d ₁ , как правило, очень консервативна, во многих приложениях можно пользоваться (5).

Теперь интересно получить решения f 1 ,f ₂ кинетических уравнений типа (2), связанные условием фрактальности этих решений

df 1 =_{- c f} df, dt ¹ t ^{1 ,}dt

^c ₂

f 2 st

f ₁ = c f ₂ ^d                        (6)

При этом d f /д^ = cdf2^{d - 1 )} . Отсюда, полагая фрактальную размерность d, не зависящей от ξ, и, учитывая (5), несложно прийти к нелинейным дифференциальным уравнениям

Об отличии модели (9) от теоретически более строгой нелинейной можно судить из сравнения их поведений в пространстве инварианта ξ . Изучение показало, что такое отличие существенно зависит от разницы фрактальных размерностей α и α ₁ в пространстве функций и их производных, соответственно. При близких размерностях ( a = 1,8 и a 1 = 1,9 ) цена линейности не превышает 0,5 %. Но при большой разнице размерностей ( a-a 1 = 0,8 ) отличие плотности, даваемой линейной моделью, от нелинейной достигает 25%. Поэтому часто справедлива частотная фрактальная зависимость (6). От нее несложно перейти к ранговой связи:

fi (r )=BP , (10)

где ^ = 1 a, a = 1 - d,B = ( D ^{1 a} )/X, D = Aj a, и, следовательно, пространство ( f 1 , f ₂ ) отобразить в пространство ( f 2 , _r ) . Здесь r - ранг, описыва-

ющий порядок убывания f ₂ (ранг операторов, встречающихся в программе x раз):

f ₂ max

r (x) = Z f (x).

r= f ₂

Значение коэффициента A поясняется фракталом n ( x ) = A,x^^+a ) , который неизбежно следует из процедуры получения (10). Ранговый фрактал (10) содержательно описывается как относительное число f ₁ = x X включений операторов языка программирования, соответствующее рангу r частоты f ₂ их использования.

3.    Модельные статистические испытания и их результаты

Обоснование фрактала (10) делает понятным содержание модельных испытаний по изучению свойств фракталов, связывающих множество операций языка программирования и множество программ.

Для модельных статистических испытаний были выбраны множества нормальных и «зараженных» программ одинаковой мощности, равной 15. В качестве элементов ПРС использовались вирусы: невидимка (типа lip.exe, acad.exe), загрузочный резидентный вирус (типа cdir.exe), файловый резидентный вирус (типа calc.exe); не самовоспроизводящиеся закладки типа FatalError, Krenx, Remote, Hookdump. В процессе испытаний идентифицировались управляющие конструкции языка Ассемблер. Нормальные программы выбирались из числа, разработанных на языке Турбо Паскаль. Пары программ (обычных и «зараженных») формировались с равновероятным законом включения, после чего проводилось решение конкретных, прикладных задач с идентификацией и оценкой частоты использования управляющих конструкций языка Ассемблер. При этом использовались соответствующие дизассемблеры. Проведено 150 испытаний, по результатам которых построены кривые мультипликативных регрессий, связывающих относительное число f 1 включений операторов языка с рангом r частоты f ₂ их использования. Кривые регрессии приведены на графиках рис. 1.

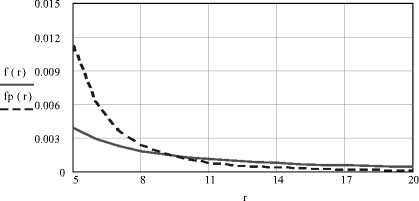
Рис. 1. Ранговые распределения операторов в обычных f ( r ) и зараженных (с ПРС) fp ( r ) программах

Количественно различие ранговых распределений операторов в обычных и программах с ПРС характеризуется фрактальными размерностями α , величины которых определяются из регрессионных зависимостей (рис. 1) для:

программ с ПРС

ln(fp) = -2,37 - 0,30ln(r); в = - 0,3;

α = 1/β = – 3,33;

нормальных программ

ln(fp) = -0,05 - 0,63ln(r);p = -Q,63;

α = 1/β = – 1,59;

По критериям, обоснованным в [5-6], множество испытанных обычных программ относится к системам с персистентным поведением, то есть характеризуется вероятностной временной стабильностью поведения. Множество же программ с ПРС наоборот эргодично, антиперсистентно; поведение их отличается большей изменчивостью.

4.    Заключение

Обоснованная фрактальная модель, базирующаяся на диффузионных уравнениях Фоккера-План-ка-Колмогорова и описывающая свойства языковых конструкций программных продуктов, позволяет проводить модельные статистические испытания по оценке различий продуктов обычных и зараженных. Проведенные компьютерные испытания множеств программ показали, что зараженные программы по фрактальной размерности существенно отличаются от обычных программ. Несмотря на ограниченность объема испытаний программ полученные результаты могут быть интересны при разработке технологий и компьютерных продуктов защиты информации.