Frequency spectrum of natural oscillations of the spatial structure of the rod pyramid

The metal truss structure has many outstanding advantages such as durability, ease of use, relatively easy installation, so it is most commonly used in construction work. Usually schemata of statically defined rigs in space are quite rare and poorly studied [1], [2]. Computational programs using symbolic mathematics with special operators such as Maple can be used to solve systems of linear equations in notation [3]–[6], applicable to such constructions. In order to obtain an analytic solution in the form of a closed formula, some simplifications need to be made when modeling the structure. As a rule, the construction is simplified to a statically defined structure. In some cases, the construction of structures such as trusses, which are statically determined and at the same time contain periodically repeating structural elements, then for such a design it is possible to obtain the calculation formulas for an arbitrary number of repeating elements. Common trusses are flat or space trusses with the same slab, but the number of panels can be very large. That is the reason, the analytical solution has a great advantage over the digital solution. The analytical solution not only saves computation time but also avoids the accumulation of rounding errors. For systems with many plates this greatly affects the calculation results. The induction method is used to obtain formulas for calculating the natural frequency of oscillations for an arbitrary number of plates. The special analytical solutions show outstanding efficiency in truss optimization problem [7]–[9]. In the citations [10], [11] present solutions for the deformation of flat truss with arbitrary number of plates obtained using the inductive method and some natural frequency problems of the results usual structure. Formulas for the natural oscillation frequency of an arbitrary number of panels are obtained by induction. Analytical solutions are especially effective in truss optimization problems [12], [13]. The inductive method is also used to calculate the natural vibration frequency of conventional structures [14], [15]. The article [16] proposes multi criteria problems of constructive optimization of trusses with a combination of new contradictory objective functions and constraints, such as natural frequencies and load factors, taking into account the overall stability of the structure. Analytical estimates from below of the first natural frequency of natural oscillations of the truss by the Dunkerley method using mathematical induction and operators of the Maple system [17]. The spectrum of natural frequencies is studied numerically [18]–[20]. In this paper, the task is to derive an analytical dependence of the oscillation frequency on the number of panels with a lower and upper estimate. The resulting formulas can be used to evaluate numerical solutions, especially for large-scale designs.

• 2    Materials and Methods

  2.1    Truss construction

2.2    Natural frequency

The truss is made up of three identical flat triangular meshes with supports on the sides of the base. The bars of the mesh do not connect at the intersection points, the hinges lie only along the edges of the mantle. The base of each face of length na is made up of n horizontal bars of length a . The height of the pyramid is nh . The structure consists of 3 n vertical support bars and three simulated spherical support rods at angle A and a cylindrical bar at angle B. The total number of bars in the structure are ν = 6 n - 18 . The total number of internal hinges of the structure is less than three times and is equal to 6 n - 2 . The number of hinge nodes on the sides of the pyramid are 3 n - 2 , the number of hinge nodes on the bottom faces is 3 n . The truss is determined statically.

z

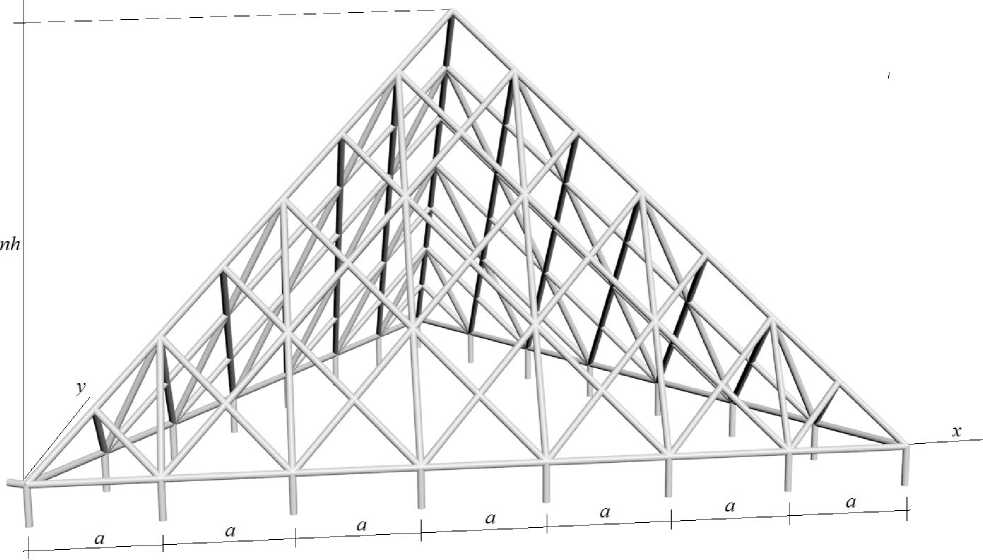
Fig. 1 – Truss, n=7

The value of the first (lowest) natural oscillation frequency is one of the most important dynamic properties in calculating the dynamics of structures. As a rule, the calculation of natural frequencies is performed numerically based on various variations of the finite element method. Analytical methods are Kirsanov, M.; Luong C.L.

Frequency spectrum of natural oscillations of the spatial structure of the rod pyramid;

only available for upper and lower frequency estimates. The essence of these methods is that they are based the calculation of the partial frequencies, the values of which in some cases can be found by analytical methods. For conventional designs, the analytical estimate can be generalized to an arbitrary number of panels by the inductive method.

The inertial properties of the structure are modeled by concentrating the mass m in the truss nodes. In the simplest formula, the masses of goods m are the same. Neglecting the horizontal displacements of the nodes, the vibrations of the nodes occur only in the vertical direction. The number of degrees of freedom of the truss weight system of order n is equal to the number of nodes K = 3 n - 2 . The dynamic equations of the mass system in matrix form are written as follows:

mI_KZ + D_KZ = 0,                                 (1)

where Z - the vector of vertical displacements of masses 1,..., K , Z — acceleration vector, IK — identity matrix, D_K — stiffness matrix. In the case of harmonic oscillations with a frequency ω , the relation Z = -ro ² Z . The matrix inverse to the stiffness matrix D_K is the compliance matrix B_K . The elements of this matrix are calculated using the Maxwell-Mohr formula:

v- 3 n - 3

• b, j = z sa° saj) ia /( ef ).                                   (2)

2.3    Dunkerley score

a= 1

Introduced standard notation: b ij — displacement of node i from the action of a single vertical dimensionless force applied to node j, S^' ) forces in rods with numbers a from the action of a unit force applied to node i , l _α – bar length with number α , EF — longitudinal stiffness, assumed to be the same for all rods.

By multiplying equation (1) by the matrix B_K , taking into account the replacement Z = -ro ² Z corresponding to harmonic vibrations:

z k = u k sin^{( ro} t + Ф о ).                                              (3)

The problem is reduced to the problem of eigenvalues of the matrix B_K : B_KZ = 1 Z , where 1 = 1/( ro ² m ) — is the eigenvalue of the matrix B k , ro — is the natural oscillation frequency. From here, the frequency of natural oscillations has the form ω= 71/( m 1 ) .

The forces Sa' ) in the truss rods included in the elements of the matrix B_K are determined from the solution of the system of equations of the truss nodes, which also includes the reactions of the supports. For a structure with an arbitrary number of panels, it is impossible to obtain analytical solutions. Approximate methods are used to obtain an estimate of the first frequency from below and from above.

The lowest estimate of the first oscillation frequency is obtained by the Dunkerley formula:

K

- 2           - 2

ω _D = ∑ ω _i ,                                     (4)

i = 1

where ω _i — frequency of oscillations of one mass m located at a node i . To calculate partial frequencies ω _i , we compose equation (1) in scalar form:

mzi + Dizi = 0, where Di — scalar stiffness coefficient ( i is the mass number). Load fluctuation frequency:

^ro i = V D i / ^m •                                                   (5)

The stiffness coefficient, the reciprocal of the compliance coefficient, is determined by the

Maxwell-Mohr formula (2):

V           2

8 i = 1/ D, = £ ( S a' ' ) l „ /( EF ) .

a= 1

K          K i

From (4) and (5) follows to - ² = ^to - ² = m^— ~     м D i

Since compliance is the reciprocal of stiffness

1/ D i = 8 , , then:

K         K V toD = m£8, = m££(S" ) la/(EF) = m£./(h2EF).

i = 1              i = 1 a= 1

K v2

Then sequentially calculate the sums £ n = h ²££ ( S a ⁱ ) ) l _a for n = 1,2, 3, 4,...

i = 1 a= 1

£ 1

(3 a ³ + c ³ ) 27

£ 2

(15 a ³ + 5 c ³) 81

£ 3 =

(21 a ³+7 c ³) 81

£ 4 =

(3 a ³ + c ³) 9

£ 5

(33 a ³ +11 c ³)

With the help of operators in the Maple program the common terms of the series of coefficients in these expressions are calculated. Get results £ _n = r a a ³ + r _c c ³ where:

2 k +1 r =.

a27

r = 2 k +1

c81 , c = aI 3 a2 + 9 h2

After finding the expressions for the coefficient (7), the Maple program is used with the help of the rgf_findrecur operator to compile the recursive equations. Using rsolve operator, it is possible to solve these equations and get the common terms of the series. It is easy to see that every element of the series is a fraction, where not only the numerator but also the denominator depends on n , in which case direct application of such an algorithm does not yield a product pole. The Maple system statements are not intended to define the common elements of such sequences. An alternative method for finding common elements of such strings is provided by the FindSequenceFunction operator in the Wolfram Mathematica notation math package. In this case, the equations have very nice solutions, allowing us to solve them without using symbolic mathematics. As a result, the lower estimate for the first Dunkerley frequency is:

ю _D

= h 1

N

EF m ( raa3 + rcc3)

• 3    Results and Discussion

  3.1    Numerical example

  To illustrate the found dependence of the frequency of natural vibrations on the number of panels and to estimate the error of the found estimates of the analytical solution, it is necessary to find the first frequency from the frequency spectrum of natural vibrations of trusses. The truss under consideration has dimensions a = 3 m , h = 8 m . The cross-sectional area of the lattice rods and support rods are assumed to be the same: F = 9 cm ² . Modulus of elasticity of steel E = 2.10 10 MPa , masses in nodes m = 150 kg . On fig. 2 shows the dependence on the number of panels of the upper estimate of the lowest frequency ю D according to Dunkerley (8) and the numerical value of the first frequency of the spectrum ю 1 found by analyzing the problem of oscillatory systems with K = 3 n - 2 degrees of freedom.

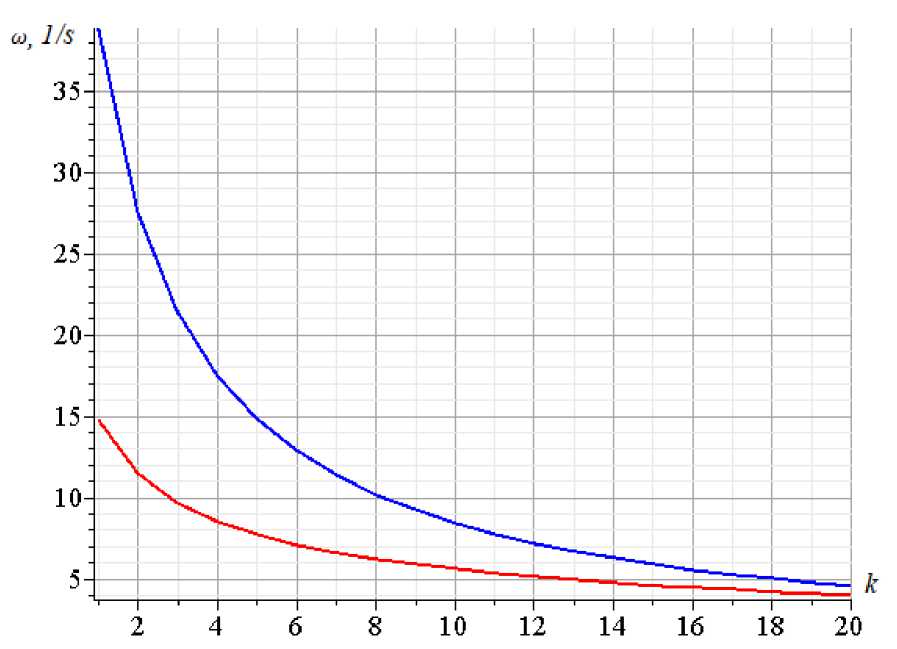
Fig. 2 - Comparison of the analytical solution with the numerical one. 1 — the lower estimate ю D according to Dunkerley at a = 3 m , h = 8 m ; 2 — frequency ю 1 obtained numerically

From the graph in Fig. 2, it can be seen that with an increase in the number of panels, the natural frequency decreases monotonically. When the number of panels is small (for example n <  6 ), the natural frequency decreases very quickly as the number of panels increases. It can also be seen that the error in the analytical estimate is usually small and decreases significantly as the number of panels increases. From this it can be concluded that the resulting analytical solution is best suited for solving problems with the truss with many panels.

In this case, with an increase in the number of truss panels, the analytical solution is especially effective, since the numerical calculation times increases exponentially, the accuracy decreases, and the accuracy of the analytical solution only grows, reaching a relative error of 2% (Fig. 3).

To clarify the error of the solution, the relative value г is mentioned. The change in this value depending on the number of panels is shown in Fig. 3. With an accuracy of 2% to 63%, the analytical evaluation gives a satisfactory result.

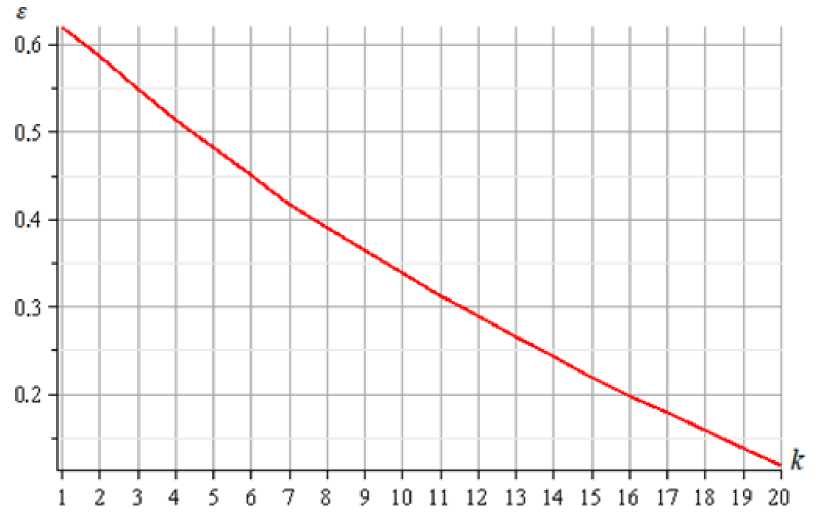
Fig. 3 – Relative error in estimating the oscillation frequency according to Dunkerley

3.2    Natural frequency spectra of regular trusses

Higher vibration frequencies are usually not used in engineering calculations, except in studies of resonant cases. The frequency of natural oscillations caused by the operation of various devices (machine tools, fans, etc.) can coincide with the frequency of natural oscillations of the structure. It is not possible to calculate these frequencies analytically, but the debugged mathematical apparatus in the numerical calculation mode gives an interesting picture of the sets of spectra of regular systems. Figure 3 shows the natural frequency spectrum of the trusses in different orders, calculated numerically. Some features of the frequency distribution are noticed here. Each curve corresponds to an ordered farm from n = 3 to n = 25 .

Alternatively, the Rayleigh method can be used for an upper estimate of the fundamental frequency. The Rayleigh method gives results with higher accuracy, but to find the dependence of these coefficients on the number of panels, the inductive method is used with rather cumbersome results [26]. The biggest difficulty in deducing the dependence of the oscillation frequency on the number of panels is the denominator. The numerator of the expression differs only from the Dunkerley method in that the deviation of the sum is calculated not from a single force acting on each node of mass, but from a load distributed over all nodes of mass. The denominator is the sum of the squares of these deviations. However, the Rayleigh method for ordinary rigs of arbitrary order is not feasible in many cases.

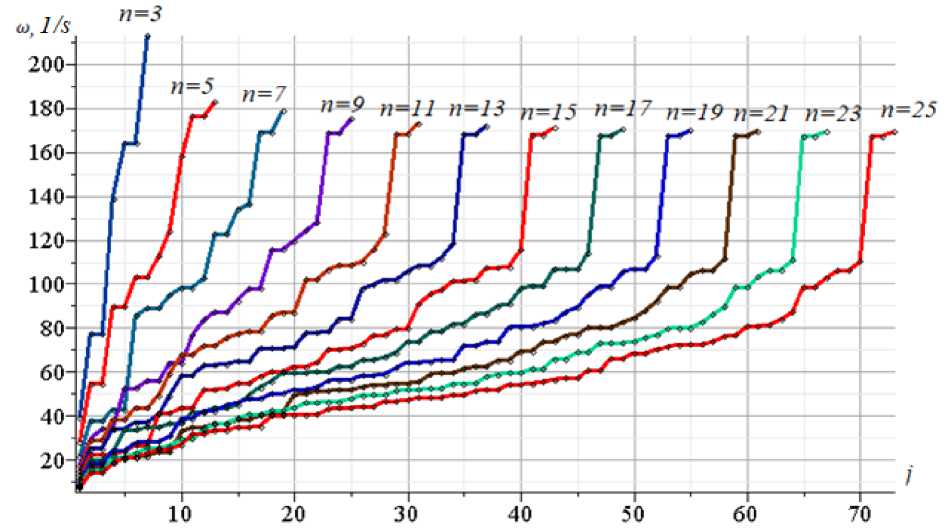
Fig. 3 – Spectra of regular trusses

The dots on the curves mark the frequency. On the n = 3 curve there are points corresponding to all K = 3 n - 2 = 7 spectral frequencies of this rig, on the n = 5 curve there are 13 points. The horizontal axis shows the number of j points in the spectrum. Typical patterns of frequency distribution patterns in the spectrum are recorded. First, when n >  5 all higher frequencies of the spectrum are multiples. Second, the truss scheme under consideration has the same spectrum-frequency constants for different ordered rigs. When n >  5 , for the accepted truss dimensions a = 3 m , h = 8 m , F = 9 sm ² , a constant frequency appear ю = 170 s ^{- 1}. The presence of this regularity allows predicting some truss frequencies (e.g., higher) of order of large regularity according to the computational data of a truss with a few tables. The first frequency has a fairly accurate analytical estimate (8), which is found by the Dunkerley formula.

• 4    Conclusions

A symmetric statically defined spatial structure diagram of pyramid form is proposed and the analytical dependence of the stress-strain state and its oscillation frequency is obtained on the number of plates. The calculation formulas found are quite common and can be applied to many similar types of structures. Using algorithms in derivation allows us to simply recompute the problem for other types of loads. The analytical estimates found for the lowest oscillation frequency show that the accuracy of the Dunkerley estimate is quite sufficient to use the obtained formula in the calculation.

The main result of the work is the calculation of the structure and analysis of the dependence of some of its stress-strain state characteristics on the number of plates. The advantage of such solutions is that it helps to analyze and select the most optimal parameters of the designed structure without using numerical solutions. One of the advantages of an analytical solution is its accuracy independence which means no dependence on the complexity of the design. In three-dimensional problems that need to be volumetric, this advantage is shown more clearly than for planar systems.

• 5 Fundings

  The work was supported by the Russian Science Foundation 22-21-00473.