Фрезерный станок с параллельной кинематикой

схемы (рис. 2) была разработана математическая модель кинематики станка, в табл. 2 указаны геометрические параметры трипода.

Таблица 1. Основные технические характеристики станка «Дельта 1»

количество линейных приводов	3
система управления	PCNC
порт управления	USB
размеры рабочей зоны (без учета вылета инструмента), мм	230x230x140
расчетная сила резания в рабочей зоне, Н	6
мощность привода фрезерной головки, Вт	450
габаритные размеры, мм	740x740х594
масса, кг	80

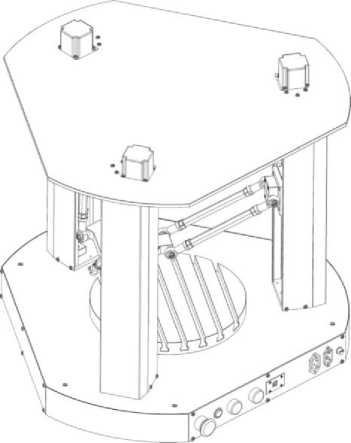
Рис. 1. Станок типа трипод «Дельта 1»

В прямой задаче по исходным заданным линейным перемещениям линейных приводов получаем положение подвижной платформы. В обратной задаче по исходным заданным координатам подвижной платформы определяем величины перемещений линейных приводов. При решении обратной задачи заданы: координаты центра (x0, y0, z0), 0≤z0≤L стороны фигуры b и с, координаты x, y точек на осях: х1 = 0; y1 = 0; х2 = ^; у2 = ^; x3 = d; y3 = 0. Необходимо

2              2                 ’ J найти z1, z2, z3. Рассчитаем координаты точек (x01, y01, z0), (x02, y02, z0), (x03, y03, z0):

Ь с хО1 = хО - ---;

л Ъ + 2с СУЗ.

уО1 = уО-—= + —;

2v 34

х02 = х0;у02 = у0 + ^-^;(1)

хОЗ = хО + - + -;

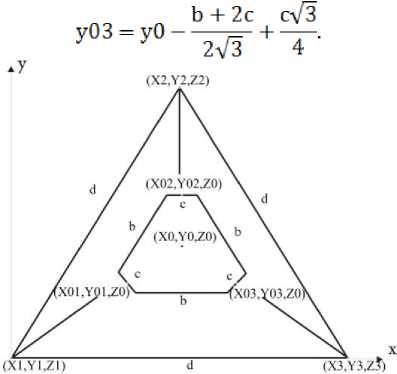
Рис. 2. Проекция звеньев трипода на плоскость OXY

Для того, чтобы подвижная платформа не пересекалась с осями звеньев необходима проверка расположения точек (x01, y01), (x02, y02), (x03, y30) внутри треугольника (рис. 2). Следовательно, должны выполняться условия:

,

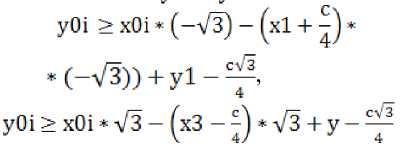
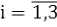
Таким образом, получено решение обратной задачи кинематики трипода, удовлетворяющее требованиям его функционирования.

При решении прямой задачи дано: z1, z2, z3. L — п — е < zi < L — е, i = 1,3 . Расстояние между (x0i, y0i, z0) и (xi, yi, zi), i = 1,3, равно a. Составим систему уравнений:

f(xl — xOl)2 + (yl — yOl)2 + (zl — zO)2 = а2 < (х2 — х02)2 + (у2 — у02)2 + (z2 — zO)2 = а2 ( (хЗ — хОЗ)2 + (уЗ — уОЗ)2 + (z3 — zO)2 = а2 (3)

Выполняя преобразования получим:

(кх * zO + сх)2 + (ку * zO + су)2 4-+z02 — 2 * zl * zO = cl;z02(kx2 + ky2 + 1) + 2z0 *

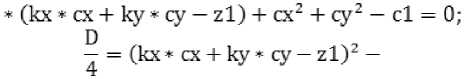
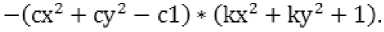
Должно выполняться: D≥0. Нам необходимо меньшее             значение             z0:

„ -(kx-cx+ky-cy-zll-v'D _ zO =                    . Необходимо также

(kx2+kyz+l)

выполнение условия: z0≥0. Таким образом, система решена. Для того, чтобы подвижная платформа не пересекалась с осями, проверим следующее условие. Через точки (x1, y1), (x2, y2), (x3, y3) проведем прямые, параллельные противолежащим сторонам d и проверим, чтобы точки (x01, y01), (x02, y02), (x03, y30) лежали внутри треугольника. Уравнения прямых:

у = X « (-V3) - (xl + ^) * (-V3)) + yl - ^,

1— (      c \ y =y2,y = x * уЗ — I x3 — 1 *

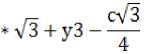
соответственно. Следовательно, должны выполняться условия:

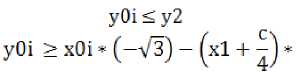
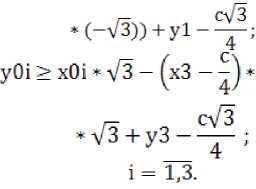
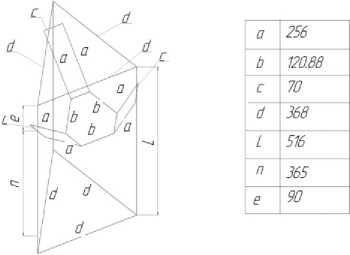
Рис. 3. Геометрическая схема разработанного трипода: а – длины штанг, b – размеры подвижной платформы; с – расстояние между штангами, L – длина линейных приводов; n – величина рабочего хода привода, e – верхняя зона ограничения перемещений; f – нижняя зона ограничения перемещений

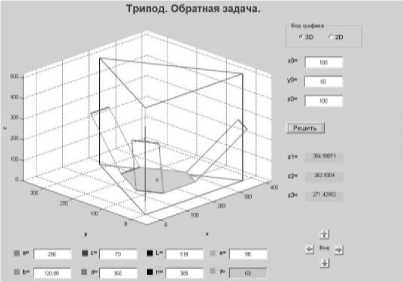
Рис. 4. Реализация примера решения обратной задачи кинематики трипода в MATLAB: x0, y0, Z0 – координаты центральной платформы, z1, z2, z3 – координаты линейных перемещений кареток

На рис. 4 представлен пример решения и интерфейс обратной задачи кинематики трипода, выполненный в программе MATLAB 7.7.0 при заданных значениях линейных модулей. В центральной части окна программы программно визуализирована геометрическая модель трипода в 3D, в правом нижнем углу находятся клавиши изменяющие угол обзора модели. На рис. 5 представлен пример решения прямой задачи. Разработанная программа обеспечивает моделирование прямой и обратной задач для любой геометрии трипода. В математической модели заложены ограничения на пересечения шарниров, линейных штанг и выноса перемещаемой платформы за пределы рабочей зоны, при которых возникает заклинивание механизма трипода. Таким образом, создан настольный манипулятор для фрезерного станка «Дельта 1» с параллельной кинематикой, разработана математическую модель его кинематики, выполнено решение прямой и обратной задач кинематики трипода, разработаны алгоритмы, программы и интерфейс для решения этих задач, выполнены численные примеры решения.

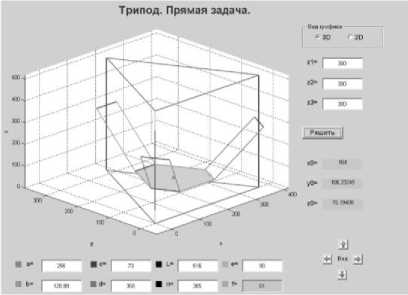
Рис. 5. Реализация примера решения прямой задачи в MATLAB