Фрикционно-диссипативные свойства камер сгорания доменных воздухонагревателей

Массовые, упругие и диссипативные свойства среды в канале камеры сгорания доменного воздухонагревателя определяются соответственно удельными акустическими параметрами: массой т_а , кг/м³, емкостью с_а , м³с²/кг и трением г_а, м³/(кг-с), которые проявляют свое влияние лишь в процессе колебаний среды относительно параметров осредненного течения. Если при определении первых двух параметров не встречается затруднений: т_а = p/s, с_а = $/рс² , где s - площадь сечения канала, м², р,с - плотность среды, кг/м³ и скорость звука, м/с в ней, то определение г_и осложнено рядом условий [1]. Для определения этих условий необходимо рассмотреть влияние вязкости среды на распространение возмущений акустического характера в канале камеры сгорания. Воспользуемся для этого методикой, изложенной в работе Я.Ш. Вахитова [2].

Выделив в канале плоского или круглого сечения элемент объема dv = b-dx-dy; dv = 2лг -dx-dr, определим разность давлений при х и х + dx , возникающей по причине возбуждения колебаний объема

( др др p-b-dy-\p + — dx \b-dy =—-b-dx-dy. (1) V дх ) дх

Силе давления противодействует, согласно второму закону Ньютона, инерционная реакция массы в объеме dv

Po-dv^ = Po"b-dx-dy^,             (2)

от              ОТ где £- скорость смещения при акустических колебаниях, м/с.

Силы вязкости приложены к верхней и нижней граням, их направление связано с тормозящим действием твердой стенки канала: на верхней грани силы вязкости тормозят колебания и имеют отрицательный знак -b-dx- x_y+dy, на нижней грани силы вязкости передают действие слоев, имеющих большую скорость, и поэтому имеют положительный знак bdxx_y.

Баланс сил, приложенных к массе в объеме dv , записывается в виде др                                 дЁ

——bdxdy-bdxx yd + bdxx = pobdxdy— . (3) дх           у у у^

Сократив на bdx, получим др         д^     {\

=        +(4)

дх         ОТ      \ у у у/

В уравнении (1) для функции давления р = <р(х) применено разложение Тейлора с учетом двух первых слагаемых t \ др д2р , х2                 ...

Р\х) = р + — dx+——y\dx) + ...;       (5)

дх 2! ОТ'

если применить этот же прием к функции ^т = /(т), ТО для x_wty получим

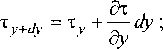
и выражение (4) приобретает вид

Полагая, что среда в канале камеры сгорания имеет свойства ньютоновской жидкости

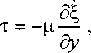
нения вязких поперечных волн уг определяется согласно (12), (13)

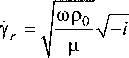
а с учетом равенства V-/ = (1 - z)/V2

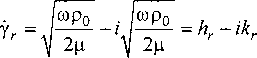
где hr и кг - коэффициент ослабления и волновое окончательно найдем уравнения движения для канала плоского сечения

др     д^   32с ох     от ду~

и для канала круглого сечения в цилиндрической

следовательно yr = hr (1-z);

системе координат

Эр    ЭЕ   (32Ё 1 ай й = Рой”Р +

Эх      от    ( 3/-     г dr j

(Ю)

Для синусоидальных колебаний Ё, = Ёое,с°т

§ = /£0^=^;(н)

дт применив подстановку (11) в (9) и (10), получим

^Ч zcopo е _ 1 Ф .(12)

дг² г дг ц ц Эх

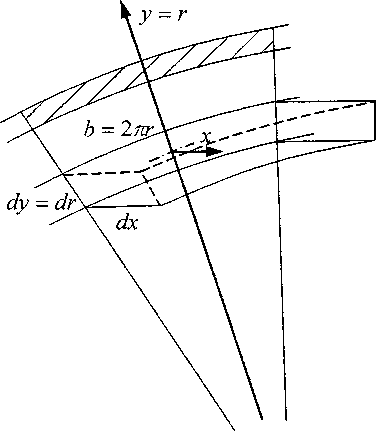
Схема к выводу выражений (12), (13)

В уравнениях (12), (13) коэффициент при Ё, характеризует распространение волн особого типа - вязких волн поперечного типа, которые вызываются продольным градиентом давления др/Эх, а распространяются в поперечном направлении к стенке канала и обратно. Постоянная распростра

число вязкой волны, причем

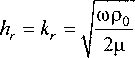
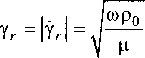
Модуль постоянной распространения уг связан с колебательным числом Рейнольдса потока среды Rem, которое в свою очередь определяется

посредством гидродинамического числа п м/Ро

Re =--- и числа Струхаля Sh = —

ц

,2           22

Ц      ЦV yrZ = Re”’5.(17)

Граничными условиями для решения уравнений (12), (13) являются "условия прилипания", т. е. неподвижность частиц среды на стенках канала

^(у)| ,=о или Ё(г)| =°;(!8)

и симметричность задачи для Цу), т.е. наличие при у = 0 (г = 0 )точки перегиба у кривой ё (у)

5|£у)

аЦЦ или ——  = 0.

дг г=0

Решения уравнений (12), (13) при граничных условиях (18), (19) имеют вид:

(20) cosyrz

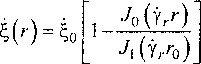
Зависимости (20), (21) описывают изменение колебательной скорости в поперечном направле

нии, причем параметр i _ 8р 1

50 - э .

ох 1е>р0

соответствует распределению скорости под действием продольного градиента давления др/дх в отсутствие вязкости среды.

Введем понятие удельного комплексного акустического сопротивления или удельного акустического импеданса

др 1 дх

между za и комплексным механическим сопро тивлением, т.е. механическим импедансом zM канала камеры сгорания площадью сечения S и длиной L при L < Х/4 , где X - длина волны воз мущения, существует зависимость i»=i«LS.                           (24)

Усредненная по координате у скорость частиц среды Е, определяется интегрированием

М^(у>ф,                 (25)

о где ^(у) или ^(г) соответствуют (20), (21).

Тогда г . др 1    1 tgy/ _ дх zopo уг/

Ф 1 1 ²Ш^го) дт/сор_о[ мЛСМ))

откуда можно получить значения удельного акустического импеданса

^Ро .

i-Mr! ’ у/

/гор0-У0(угг0)

ТА

Выражения (28), (29) весьма сложны для прямого анализа, так как za как функция комплексно го аргумента уг7 (yrro) сам является комплексным числом. Априорно можно отметить, что соотношение между действительной и мнимой частями зависит от соотношения вязкостных и инерционных свойств среды, проявляющихся при распространении вязких волн поперечного типа. Поскольку число Rero отражает отношение инерци онных сил к силам вязкости, то при малых числах Reo следует ожидать преобладающего влияния вязкости, т.е. преобладания активного сопротивления в zo, а при больших Rera - преобладающего влияния инерционно-массовых сил и большой величины реактивного сопротивления в za.

Для последующего анализа зависимости гя=<р(КеС)) необходимо произвести оценку реальных значений Reto =о/2р0/р, где р0 и ц являются функциями состава и температуры среды в канале камеры сгорания; индекс «0» при р означает, что плотность среды берется при статическом давлении в камере сгорания. Будем исследовать диапазон частот 2-100 Гц при поперечных размерах / = г0=1,0-3,0 м и температурах 12001600 °C, причем без большого ущерба для точности оценочных расчетов свойства среды можно приравнять к свойствам продуктов сгорания среднего состава (13 %СО2, 11%Н2О, остальное -азот).

Минимальным значениям Re_ra отвечают ® = 2гс-2 = 12,56 рад/с; t =1600 °C, /=1,0м; максимальным - ю = 628 рад/с, t = 1200 °C, / = 3,0 м.

Подставив эти значения, получим

Re™11 =38,9-103;        Re"™ =25,6 ТО6.

Для больших значений Rem используем пред ставление tgyr/ = tg[/zr/(l -/)] = .

sin Д/’Ch h_rl-icos ИД-^Хх h_rl

= —i------^r-------- (j0) sin h_rL sh h_rl-i cos /z_r/-ch h_rl

Если аргумент h_rl -> oo, то sh h_rl -> ch h_rl и tgy_rZ->(-z).

Тогда зависимость для удельного акустического импеданса принимает вид

Л,= ----у- = «оРо ----г^- =z®Po ^{1 +} тл7 • (31)

!L 1__L I лЗ)

1^3 v лЗ,

В (31) для 1/1—— / V лЗ жение в степенный ряд

1       1           ’

• -— = 1+Х + Х + -1-Х

  использовано разло-

  
  

1 _ 1 ___________1__________

ЛЗ ^г^-^ (z+ l)(O,5Re_m)⁰’⁵

Подставив в (31) значение

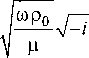
• (14) с учетом V-? = (l + z)/V2, получим

= ^у2б^Ц^мРп+^Д^^         О²)

Таким образом, при больших Rem удельный акустический импеданс состоит из активной jV^Pob =^7(2Reco)

и реактивной состав

ляющих, причем, реактивная составляющая в ш, /г_я = 1 + (0,5Re₀, )°’⁵ = (0,5Re_m )°’⁵ раз больше активной. Для минимальных для канала камеры сгорания значений R^e™ⁿ = 3 8,9 • 10^J т, [Гц = 2,4 • 10² для максимальных

Re^™ = 25,6-ю6 /и,/г(, = 3,57-103.

Аналогично для цилиндрических каналов при угг0 >10, воспользовавшись известным в теории функций Бесселя [3] соотношением

^1(угГ0) = ^(ул7=7) = получим

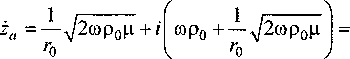
= 4{(2ReJ’5+zTReto+(2ReJ°’5l (34) r0 I L

То есть, выводы относительно активной и реактивной составляющих удельного акустического импеданса справедливы и для цилиндрических каналов радиуса г0.

Анализируя зависимости для zQ (32) и (34) можно отметить, что модуль реактивной составляющей складывается из юр0 , т. е. чисто инерци онной составляющей среды с плотностью р0 и небольшой добавки, численно равной активной составляющей импеданса, т. е.

^Га = jV^PoP '

Этот эффект можно представить как возрастание плотности среды от р0 до некоторого эффектив ного значения рЭф:

V2®PoP        1 / 2ц )

Рэф=Ро+---;— = Ро 1 + 7.--- = о/          ' уюРо)

= Ро[1 + (О,5Кею)"°-5],                 (35)

что имеет результатом снижение скорости звука от Со = Д° ^сэф = V^$Pct/^ > где ^ж = с_р /c_v - показатель адиабаты,

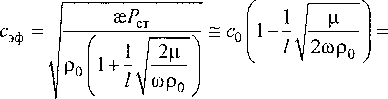
= со[1-(2Кесо)-°’5].                     (36)

Определим затухание колебаний в канале камеры сгорания. В соответствии с определением удельного акустического импеданса (23) и Z„ =г_а -НЮРэф

• -^ = ^ = (о+№^рэф)^ •          (37)

• • д£

Заменив iroE, на — согласно (11), имеем 5т

=   +                            (38)

ОХ           от

Обозначим коэффициент объемной упругости

F др среды Е = р0 — и представим, что давление в др функции времени т и плотности р можно запи-

_             dp Эр др „ сать в общем виде как — = —--. Тогда уравне- dt др дт ние сплошности для рассматриваемого случая одномерной задачи можно написать в виде дт ° Эх ’ и поэтому

_Ф =£д| дт Эх

Продифференцировав (40) по х, а (38) по т, в

Э1 р левых частях равенств получим--. Прирав-5x5т няв их правые части, получим уравнение движения для продольных колебаний среды в канале камеры сгорания д2^5?

Рэф 5т2            Эх2’ или

где сзф

Е Рр

Ро Рэф

у Рэф

Полученное уравнение (42), эквивалентное уравнению

^(5П + га -(8К)--—(5К) = 0, (43) дт          дт са Эх из [1] при замене р на рЭф и с на сэф дает возможность определить затухание гармонических ,    „         5^ . л 52^ ,. \2 „ колебании при — = квЕ, и —у = (гю) Под-

5т            5т*

д2Е 7 - становка —т = (/о)-| в (42) дает 5г2

■ i® U ^а где у_Л =--- 1--— .

сэф у ® Рэф

Согласно (35) и (36) поправка к плотности и скорости звука в среде с увеличением числа Кеи убывает и при больших числах Кею становится пренебрежимо малой, поэтому можно полагать, что при Reo »10,

Рэф — Ро ’ ^эф ™ Со )

«Рэф •

Тогда

■  I—^: F у 2

zee iru _ ио wu          ra ~ у^ _ ---- I ]--_ ---- |--q--^ ^ . _ сэф^ ®Рэф Сэф^ 2ю Рэф J  4ю-р;ф

=      + z — = hx+ikx.(46)

2р0с0 с0

Решение уравнения (44)

Цх) = Ае"'^ а-В^^(47)

имеет смысл прямой и отраженной волн. Ограничившись рассмотрением лишь прямой волны

Цх^ = Ае"^1 = Ае"1у -е"^, найдем ее пространственный коэффициент затуха ния hx = —“— и волновое число кх = —. Так 2р0с0с как, согласно (32) ra = ~^(^ Кеш)°5 =то p^ReJ0,5 ,(49)

2/ Р0с0

где р_ос_о - волновое сопротивление канала камеры сгорания при движении в нем плоской звуковой волны. Размерность h_x - 1/м, величина обратная h_x

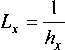
2/ Р0с0

R(2Reo>)0-5

имеет размерность м, она равна расстоянию, которое пробегает звуковая волна при нанесении единичного синусоидального возмущения при уменьшении амплитуды волны в е = 2,72 раза. Подставив значения величин при t = 1600 °C, получим L_x = 10⁴ м.

Таким образом, фрикционно-диссипативные свойства канала камеры сгорания доменного воздухонагревателя характеризуются весьма малым затуханием колебаний собственной частоты, что объясняет тот экспериментальный факт, что гидродинамические процессы в воздухонагревателях легко входят в режим автоколебаний при благоприятном амплитудно-фазовом соотношении сигналов прямой и обратной связи.