From a Robinson Crusoe economy to a pure exchange economy

From a Robinson Crusoe economy to an exchange economy

We propose the Robinson Crusoe model [1; 2; 3] as a starting point of pure economic theory. At the same time, we imply that this model allows us to determine essential features in the behavior not only of an isolated individual, but of a person in general and, therefore, a social person. In turn, the understanding of crucial aspects of human economic behavior, obtained on the basis of the Crusoe model, should help to identify those internal forces that encourage an individual to enter into economic relations with other people. Only in this case will the Robinson Crusoe model actually become the first step in the building of pure economic theory.

One of the questions that arises when we try to implement such a research program consists in determining basic features of the economic system, from the analysis of which we will proceed further.

Upon closer examination, it turns out that this question is not so simple. When trying to resolve it, we first of all face the fact that the benefits (namely, they are the driving force of human behavior) that an individual can derive from interaction with his fellow human beings are directly dependent on the institutional framework in which this interaction is taking place. It is one thing if a certain group of people considers the fruits of productive activity as a common property, and another thing if everyone assumes that the product of one’s activity is one’s own property. In other words, the form of a social economy that logically follows the Crusoe model should be determined by the basic economic institutions1 [1, p. 33].

Since we are interested in the market economy, we will proceed from the fact that the members of society are free people who make decisions independently, respect private property (thus, we do not consider the problems of non-economic coercion) and are responsible for the obligations they have assumed.

The institution of private property undoubtedly plays an important part in the emergence of exchange relations, but is this institution a sufficient condition for them? Representatives of classical political economy tended to give a negative answer to this question. They linked the existence of exchange to the social division of labor, apparently because members of society in such conditions have no other way to satisfy their multilateral needs, except by redistributing the goods they produce through exchange. Such an approach was quite natural in the conditions of the dominance of the labor theory of value. The inability to quantify human needs made it necessary to look for the roots of exchange exclusively in the effect resulting from the specialization of producers. Accordingly, the equilibrium proportions of the exchange of goods were explained solely by labor input for production

(cost); as for the exchange, which was not based on the division of labor, it was considered “random” in the full sense of the word [5, pp. 57–72].

Apparently, this is why K. Marx, in Das Kapital , when analyzing the basic properties of goods, took the model of "simple exchange of commodities" as the basis; he considered the model as a system of individual producers connected by the social division of labor [5, pp. 43–156]. This form of economic setup should undoubtedly occupy an important place in pure theory, but there are doubts about whether it is enough to explain its emergence by simply referring to the effect resulting from specialization in the production of individual goods?

The negative answer to this question became obvious as a result of the “marginalist revolution” and, in particular, after the emergence of ordinal utility theory. There emerged an understanding that commodity exchange is not an addition to the social division of labor; it has an independent value. Accordingly, “pure trade”, in which production acts as an exogenous factor, is put on solid foundations and, in this sense, is deprived of randomness. Moreover, in this paradigm, the effect of exchange becomes an impetus for the development of the division of labor, rather than vice versa.

In view of the above, there is an intermediate point between the Crusoe model and "simple exchange of commodities" model based on the social division of labor; this point is represented by an economic system in which there are many isolated economic agents who have the right of ownership of the results of their labor. In other words, we are talking about the “economy of m Robinsons”, each of which:

• •    has a system of individual preferences with characteristics axiomatically introduced by V. Pareto;

• •    has production capabilities that allow them to produce various types of goods.

The analysis of this model is logically divided into two stages. In the course of the first stage, which is the subject of our article, the emphasis will be placed on a consistent study of the “pure trade” model. At the next stage, we will trace the development of the system of categories of “exchange economy” in the conditions of transformation of production from an exogenous to an endogenous factor. In both cases, the task is to continue building an ordered system of categories of a market economy in the spirit of the paradigm of pure economic theory, based on the available achievements of economic science, which was started within the framework of studies on the Crusoe model.

This task is fundamentally different from the one that is addressed in numerous articles aimed at studying exchange transactions from a game-theoretic point of view. Within the framework of such works, emphasis is placed on identifying strategies of behavior of exchange participants in a variety of institutional conditions, in particular those formed by various auction structures. The results obtained turn out to be a function of assumptions regarding the framework in which the subjects of exchange operate, and the general problem of exchange breaks down into countless special cases. The conclusions of such studies are undoubtedly useful for application in individual case studies, but they can hardly help in any way when attempts are made to develop an orderly view of the economic system. In the same cases, when game-theoretic approaches are implemented on the basis of Nash’s “bargaining solution” [6], they also explicitly violate the axiom of the inadmissibility of interpersonal comparisons of individual utility levels.

And the last introductory remark concerning those features of individual preferences, which we will rely on during the analysis. Essentially, there are two possibilities here. In accordance with the first one, the subject of attention is A. Smith’s “economic man”, aimed at maximizing individual welfare that is identified exclusively with the amount of own consumption. The second possibility is associated with the orientation to a more complex system of individual preferences, covering both one’s own consumption and the welfare of other members of society; such an individual could be called a “social man”.

At this stage of the study, the choice should be made in favor of the “economic man”. This is not only (and not so much) associated with the desire to facilitate the task being solved by abstracting from the “humane component” of our individual preferences. More importantly, the market mechanism is able to identify only the “selfish” part of our preferences; accordingly, it is the model of “economic man” that is adequate to the task of determining the nature of this social mechanism. Subsequent stages of the study will deal with the consequences that the functioning of the economic system will encounter due to the presence of a “social” component in individual preferences.

“Pure trade” as an exchange of bundles of goods

So, we are dealing with a society consisting of members, each of whom has a bundle of goods e_ik , where i is the number of the good ( i = 1 , …, n ), k is the number of the member of a society ( k = 1 , …, m ). At the same time, individual systems of preferences of economic agents are expressed by utility functions U_k ( x _{1 k} , …, x_nk ), where x_ik is the amount of the i -th good consumed by the k -th member of society.

The theory of pure trade allowed to get an answer to the question of whether it is possible, as a result of the redistribution of goods through exchange, to increase the level of welfare of at least one member of society without reducing the welfare of the rest2. Given that exchange is a bilateral act, the object of analysis is often narrowed down to two people (“Robinson” and “Friday”), and the model itself is formulated as follows, see, for example, [7, pp. 578–579]:

Max Up = Up(x^p, ..., xnp)(1)

under the restrictions:

Ur(xir, — • xnR) = UR(2)

• *1R + Xip = ei

xir + xtF = et(4)

xnR + xnF = ^n where UF is the value of Friday’s utility to be maximized, U§ is the level of Robinson’s utility established on the basis of the initial distribution of goods, ei = eiR + eiF is the total amount of the i-th good initially available to Friday and Robinson.

The standard procedure – the solution of a system of equations composed of the first partial derivatives of the Lagrange function³ equated to zero, allows us not only to determine the desired values of x_iR and x_iF , but also to establish the fact that in the optimal position the marginal rates of substitution of the j -th good for the i-th will be the same for Robinson and Friday:

_ № / a^ 1 = dx j =  ra^ /Щ ₍₆₎

ax _iR/ ax j_R     ax _t       ax _iF/ ax j_F

The model that provides for maximizing the welfare of Robinson while maintaining the utility level of Friday will be symmetrical. Based on this model, we can obtain a new distribution of goods between the exchange participants, and consequently, the exchange vectors ^k = (%1k - e1k, —, xnk - enk) that link it to the original distribution (k = R, F). It is clear that in this case, the new distribution of goods between the exchange participants will correspond to the equality of the marginal rates of substitution of the i-th good with the j-th good available to Robinson and Friday.

Along with the considered “extreme” possibilities, in which one of the subjects of the exchange wins, and the other retains the same position, there are many exchange vectors that provide a (utility) gain for each of them. Any element of this set can be found if we present the first restriction of the model – equation (2) – in the following form:

U r (% ir , ■■■, x_nR) = U⁰^q , (7)

where q is a parameter whose possible value is limited both from above and from below: 1 <  q <  q _max . With q = 1, we get a situation in which Friday’s utility reaches its maximum value while the level of Robinson’s welfare remains unchanged. The value of the upper limit q_max is determined by the requirement that the maximized utility of Friday does not fall below the initial level. In other words, at q = q_max , Robinson’s welfare level will be the maximum at an unchanged welfare level of Friday.

Thus, the described approach to determining the pure trade effect allows us to draw a number of important conclusions. It becomes clear that the very existence of this effect is due to the initial difference in the comparative assessment of benefits by potential exchange participants, because the exchange opportunities are exhausted at the moment when these differences disappear. In connection with the implementation of this approach, it also becomes possible to naturally introduce the concept of a contract surface (a curve – for the case of two goods), to show that all points belonging to it represent Pareto-efficient distributions of consumer goods between exchange participants.

At the same time, we have not encountered any cases when attention would be drawn to the fact that this model implicitly assumes that the object of exchange is represented by bundles of goods rather than individual goods. But this is really so: in the conditions of the model represented by formulas (1)–(5) there are no proportions of the exchange of individual goods for each other. In general, they cannot be determined from the resulting exchange vectors4. Accordingly, with the help of this approach, it is not possible to introduce the concepts of exchange value of goods and the state of general equilibrium, which are fundamental in a market economy. The question remains open as to which point of the contract surface the exchange relations of its participants will lead to. Finally, it is difficult to imagine how exchange participants can form an acceptable exchange vector in practice. In other words, a curious situation arises when there is a theoretical solution to the problem, but there is no practical one5!

Classic commodity exchange

Another, more realistic possibility of redistribution of goods between two economic agents is associated with a series of classic market exchanges, involving the exchange of one good for another in separate transactions. The basis for such an exchange is different assessment of the marginal value of the corresponding goods by the participants (inequality of the marginal rates of substitution of one of the goods for another). In view of the above, each of the numerous acts of exchange cannot worsen the situation of any of the participants. It is also clear that the possibilities of a series of exchanges will be exhausted when the marginal rates of substitution will be the same for both its participants. Thus, as in the case of the exchange of bundles of goods, pure trade carried out in the format of “good for good” must inevitably end on the contract surface.

Classic exchange equates a certain amount of one good to a certain amount of another good. Therefore, its integral feature is the proportion of exchange based on which the concept of the exchange value of an individual good6 is introduced in economic theory. As for the quantitative dimension of exchange values, so far we can only state that they should be between the marginal individual rates of substitution for each other of the exchanged goods, since otherwise the exchange would be unprofitable to one of its participants. There is also the question of whether the sequence of individual acts of exchange in the process of approaching the contract surface matters.

Economic theory, in fact, has developed two approaches that allow us to formulate certain, but different answers to both of these questions.

The first approach, founded by L. Walras [8], consists in determining the equilibrium proportions of exchange, transferring the economic system in question from the initial position to such a distribution of goods in which none of the participants in the exchange is interested in its continuation. If such a vector of exchange proportions is found, then economic agents can be granted the right to make transactions with their usage; and regardless of the sequence of such transactions, the end result will be the same. But it is also possible to simply redistribute goods between economic agents, relying on the values of the functions of pure individual demand for each of the goods corresponding to the equilibrium proportions of exchange. In the latter case, on a new basis – after all, we proceed from the exchange values of individual goods – we return to the exchange of their bundles.

As it turned out in the course of intensive research conducted in the second half of the 20th century, the question of the presence and number of general equilibrium states (and, consequently, vectors of equilibrium exchange values) turned out to be much more complicated than it seemed to the author of the theory. The equations in the L. Walras model are not linear, and therefore a simple reference to equality in the system of the number of equations and independent variables does not allow us to make a conclusion that there is a single equilibrium vector of exchange values.

First of all, on the basis of Brouwer’s fixed-point theorem, it was proven that the strict convexity of consumer preferences is a sufficient condition for the existence of a state (states) of general equilibrium [9; 10] in the pure trade model.

In the course of further research, attention was drawn to the specifics of the market functions of pure demand. Through the efforts of H. Sonnens-chein [11; 12], R. Mantel [13], G. Debreu [14], it was found that the mandatory properties of such functions are limited by the fact that they are homogeneous of zero order, continuous, and that they satisfy the requirements of Walras’ law. This means that the maximizing behavior of economic agents does not impose restrictions on the specific shape of these curves; therefore, they may not be monotonically decreasing in the exchange value of a corresponding good. In other words, in the process of aggregating individual functions of pure demand, some of the important functions of the latter may be lost.

In the development of this theorem, it was found that “regular economies”7 will have a finite odd number of general equilibrium states [15; 16], and all states will be characterized by local uniqueness, but some of them will not have the property of stability under the accepted rule of establishing the proportions of exchange8.

For two reasons, we can leave these mathematical subtleties aside for now. First, the abovementioned problems related to the specifics of market functions of pure demand have nothing to do with the “reduced” Robinson – Friday model: after all, only one person makes a demand for each good in the model; therefore, there is no aggregation problem mentioned above. Second, much more important for us is the question of how Robinson and Friday can determine the equilibrium proportions of the exchange? Are there institutional mechanisms to solve this problem?

As we know, L. Walras proposed a well-known auction model that helps to find equilibrium proportions of an exchange (it is clear that in the Robinson – Friday model, the functions of the Walrasian auctioneer should be performed by one of the exchange participants). In this case, we are faced with a very interesting problem: can an institutional structure that has no chance of practical implementation (at least in its immediate form9) be theoretically valuable? And we have every reason to give a positive answer to this question. First, because L. Walras’ “unrealistic” proposal helps us to clearly see the problem at hand: the need to identify the reaction of economic agents to various vectors of exchange values of goods by institutional methods. Second, it makes us think about the reasons for the practical inapplicability of the proposed mechanism. The answer, of course, is simple: the auctioneer and economic agents must incur enormous losses of time and effort to collect and process the necessary information. But its very articulation directly urges us to introduce a very theoretically important concept of system costs10, which in economics expresses phenomena analogous to friction in mechanics.

The second approach to the redistribution of goods between their owners on the basis of classical exchange allows for a consistent movement toward the contractual surface with the help of a series of exchanges, within which exchange values are adjusted thus satisfying the interests of the participants. Let us look at it first on the example of a situation where Robinson and Friday have two goods at their disposal, and then let us move on to the case with n goods. At the same time, we will proceed from the fact that each participant in the exchange has an adequate idea of their own preferences and does not have one with respect to the preferences of their counterpart.

Let us assume that MUR = (MU1R, MU2R) and MUF = (MU1F, MU2F) are the vectors of marginal utilities of goods available prior to the exchange, respectively, of Robinson and Friday. Then the absolute values of the marginal rates of the substi- tution of the 1st good by the 2nd will be equal to MU1R MU^p

1^м”% /«« 1= mu ; ^and l™W ) _f|= м2; . ^{If we} assume that for both potential participants of the exchange the individual exchange value of the second good EV ₂ equals 1, then these values for them will determine the marginal comparative assessment (individual exchange value) of the first good: EV_1R = |МЯ5_(2/1)я| и EV_1F = \MRS _(2/1)f \ .

In the course of communication, Robinson and Friday realize that the comparative assessments of the two goods – 1st and 2nd – do not coincide. Let us say Robinson evaluates good 1 relatively higher than Friday, that is EV_1R >  EV_1F . This state of affairs is the basis for a transaction in which Robinson exchanges a certain amount of good 2 belonging to him for a certain amount of good 1 belonging to Friday. Let us call the proportion of the exchange of good 2 for good 1 the social exchange value of good 1, expressed through good 2 – EV _{1 S} . So that the exchange was beneficial to both parties, its value should be in the range EV _1F <  EV _1S <  EV _1R . Or else: EV_1S = EV_1R • r + EV 1F • (r - 1) , 0 1 .

Let us assume that during the bargaining, Robinson and Friday managed to agree on a certain proportion of the exchange, which is within the specified limits. The question arises: what will be the quantitative parameters of the exchange?

If we proceed from the logic of the exchange of bundles of goods, then we can conclude that the exhaustion of exchange opportunities will occur at the intersection of a straight line drawn from the point of the initial distribution of goods with an inclination to the x axis corresponding to the agreed proportion of exchange and the contract curve. However, such a result will take place only in one case, namely, if the agreed proportion of exchange accidentally turns out to be equilibrium. In all other cases, the exhaustion of exchange opportunities will occur for one of the participants earlier. Indeed, the behavior of both Robinson and Friday will be described by the following model:

Max U^k(x_1k , x_2k ) (8)

with the constraint:

e ik • ^EV is + (? 2 _k = X i _k • ^EV i _S + X 2 _k , (9)

where Uᵏ is the utility value of the k-th exchange participant (k = R, F), eik is the initial amount of the i-th good of the k-th exchange participant, xik is the amount of good after the exchange is completed. The restriction presented by formula (9) is due to the fact that the exchange value of the bundle of goods available before the exchange must equal the exchange value of the set of goods after the exchange. At the same time, it should be remembered that we have agreed to consider the exchange value of the second good equal to one.

The Lagrange function for this model will have the following form:

3 = U^{k (}x_rk , X 2 _k ) + Л • [(e_lfc ^— X i _k ) • EV i _S + (ю) + ^e 2k ^{- X} 2k ^]

Let us now determine the necessary conditions (they are sufficient due to the quasi-concavity of the objective function) for the maximum of utility function (8), equating the partial derivatives of the Lagrange function to zero:

8^

5 x_lk = ^^-^•^ is = ⁰ (ID

8Uk

³ ' 2* = а^^-я = ^{0       (12)}

3 л = (e i_k ^- X i_k ) • EV i_S + (? 2_k -X 2_k = 0 (13)

Then we transfer the second terms of equations (11) and (12) to the right side and divide equation (12) by equation (11):

8U^k /8U^k             1

a^ ;; /a^ ;; == ж ⁽¹⁴⁾

Thus, the exchange opportunities for the k -th participant will be exhausted at the moment when the marginal rate of substitution of the first good with the second one turns out to be equal to the ratio of the exchange values of the second good to the first one.

Solution of the system of equations (11) – (13) allows us to determine the value of each good that maximizes the welfare of the k-th economic agent as a function of their quantities available before the exchange and the agreed proportions of the exchange (the demand function for the good):

x lk = ^x ik ^(e ik , 6 2k , EV_1S ) ,        (1⁵⁾

^ 2к = ^х 2к (е^, в 2 _к , EV 1S ) ,        (16)

where the sign * means that we are talking about the optimal amount of the corresponding good.

Here we can introduce individual functions of pure demand of the k -th economic agent for every good that will characterize those amounts of the good that the agent would like to get in the exchange (+) or transfer in exchange for another good (-):

^z 1k = ^х 1к - ^е 1к ,           ⁽¹⁷⁾

^z 2k = ^к - ^е 2к ,          ⁽¹⁸⁾

Now it is the turn of the aggregate pure demand function for each good, which is the sum of individual pure demand functions:

• ■ 1 = ^Z 1R + ^Z 1F = (^ 1R - ^e 1R ) + (^ lR - ^e 1F ) О⁹ )

Z 2 = z_2R + z_2F = (x_2R - e_2R ) + (x_2F - e_2F ) (20)

It is obvious that in the two-goods model under consideration, if one of the values of Zⁱ is zero, then the value of the aggregate pure demand for another good will also be zero (manifestation of Walras’ law). But such a state of affairs is possible only if the proportion of exchange, determined by the ratio of EV25 = 1

the social exchange values of two goods — 2:---- —

EV1S is equilibrium. In all other cases, the amount of goods exchanged will be limited by the capabilities of the “weakest party”.

The latter circumstance can be illustrated graphically using the Edgeworth box diagram (Figure).

The initial distribution of good 1 and good 2 between Robinson (the origin of the system of axes at point O ₁) and Friday (the origin of the system of axes at point O ₂) is given by point A . The proportion of the exchange of good 2 ( y axis) for good 1 ( x axis), equal to the slope of straight line AD , is equilibrium – when it is used, the exchange ends on the contract curve at point D , where the

Graphical representation of the conclusion about the multitude of trajectories of movement to the state of general equilibrium

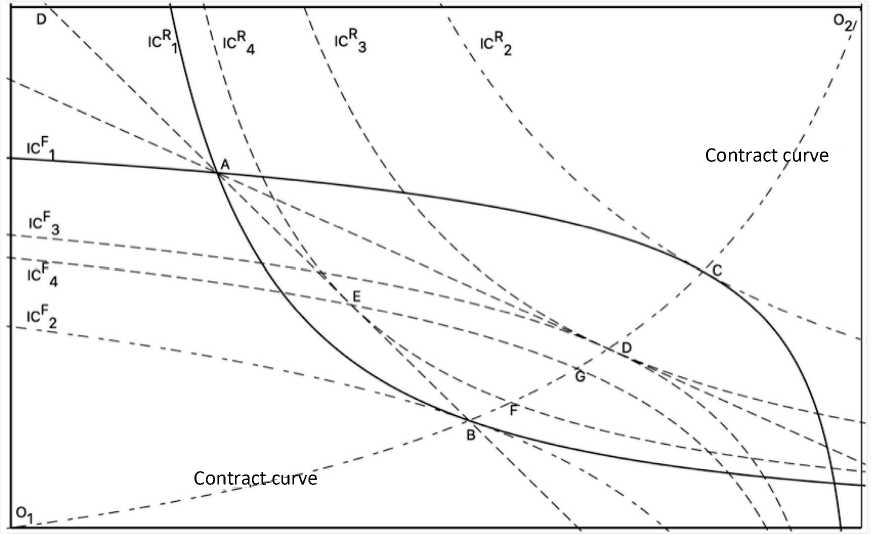
marginal rates of substitution of the second good for the first for both exchange participants are equal to this proportion of exchange.

With the proportion of exchange corresponding to the slope of straight line AB , the exchange does not end at point B , as one might assume if relying on the first approach based on the exchange of not individual goods, but their bundles. The result of applying this proportion of exchange will be the transition from point A to point E : it is here that the “weak party”, which turns out to be Robinson, is characterized by the fact that the marginal rate of substitution of good 1 with good 2 coincides with this proportion of exchange.

The specific feature of point E in comparison with the point of initial distribution of goods A is that, first, it is closer to the contract curve O ₁ O ₂ and, second, the corresponding set of points on the contract curve, which can be reached as a result of subsequent acts of exchange, narrows to interval FG .

The transition from point A to point E does not mean the completion of the acts of exchange between Robinson and Friday. With a new distribution of goods, the difference in the marginal rates of substitution of the first good with the second for these two actors of exchange creates the necessary prerequisites for its continuation. At the same time, the proportion of mutually beneficial exchange turns out to be “squeezed” in a narrower framework than before, determined by the slopes of indifference curves of Robinson (IC4R ) and Friday (IC4F ) at point E. The new distribution of goods (not shown in the graph) between the exchange participants will be even closer to contract curve O1O2, and the corresponding interval on the contract curve is even narrower. Taking into account the above, it becomes obvious that in the limit, in the absence of transaction costs, a sequential series of exchanges will lead to one of the points on the contract curve, and this point will necessarily be the point of general equilibrium. The latter statement is related to the fact that the marginal, “final” proportion of exchange will be equal to the marginal rate of substitution of good 1 with good 2, that is, it will be equilibrium.

Thus, a sequential series of exchange acts forms the trajectory of movement from the point characterizing the initial distribution of benefits between Robinson and Friday to one of the points of the contract curve. It is impossible to determine what this trajectory will be in advance, since it depends on the specific proportions of the exchange that its participants will establish at each of the “nodal points” similar to points A and E in the Figure. Only the following can be unequivocally stated:

• •    direct transition from the “nodal point” to a point on the contract line (similar to the transition from point A to point D ) will take place only if the exchange participants guessed its equilibrium proportion;

• •    the trajectory of a sequential series of exchange acts will necessarily end on the contract curve at the point of general equilibrium.

Technically speaking, the transition from the two-goods exchange model under consideration to a multi-goods exchange model does not cause any difficulties. Perhaps we should note only the fact that with an increase in the number of goods available to Robinson and Friday the degree of uncertainty of the final result of a series of exchanges between them increases even more. First, the number of transactions that they have to make increases (and each of them is characterized by uncertainty regarding the choice of a specific proportion of exchange); and second, the sequence in which they will exchange various pairs of goods becomes important.

We cannot say that these conclusions are fundamentally new to economic theory. According to the analysis of the expanded model of the exchange economy, F. Hahn and F. Fisher [18] have long established that the assumption of exchange at non-equilibrium prices changes the idea of the states of general equilibrium achievable with the initially given distribution of goods between economic agents. F. Hahn came to this conclusion, proceeding from the modified model of the Walrasian auctioneer [19, pp. 192–201). The change he made to the “groping process” consisted in the fact that after the auctioneer announces the price vector, it is allowed for willing economic agents to make real transactions using them. As a result, a new vector of exchange proportions is announced by the auctioneer already with a different distribution of resources than before. It is easy to notice that the difference from the above procedure consists mainly in who determines the proportions of the exchange – the economic agents themselves or a “third party” in the form of the Walrasian auctioneer.

Competition and its role

The analysis of the pure trade model allows us to get the initial idea of such an important phenomenon of the market economy as competition. However, this possibility arises when considering the “expanded” model of exchange economy, in which the number of economic agents is more than two ( m > 2): Robinson and Friday have no competitors!

Competition between economic agents, and at this stage of the study they act both as owners of goods and as their consumers, is generated by their desire to maximize the level of welfare by achieving the best exchange conditions. In the extreme case, no transaction will be made until its participants are convinced that there are no better conditions for the realization of their own aspirations.

The mechanism of such competition can be represented as follows (see, for example [20, pp. 398–401). A potential participant in exchange relations forms a vector of marginal rates of substitution of the good used as the counter (numeraire) with other goods. Due to the concentration of trading entities in one place, each of them has a fundamental opportunity to take into account possible conditions for concluding a similar transaction with other members of the society before concluding a transaction with one of the counterparties. The process of such comparisons (analogous to the process of tatonnement (groping) in a Walrasian auctioneer model) and making changes to the original plans (manifestation of competition) will inevitably be very long and timeconsuming, because it will affect all economic agents. However, putting this circumstance aside, we consider it logical to conclude that such competition between numerous participants in pure exchange should lead to the formation of uniform proportions of exchange (including trans-temporal) on the market, providing a direct transition from the initial distribution of goods to one that corresponds to the state of general equilibrium11.

In this context, it seems logical to introduce the concept of the market as a special place for making transactions (the equivalent of the term “marketplace” used in English-language literature). The concentration of the owners of goods in one place and at one time to reach agreements on the exchange allows each of them, on the one hand, to minimize the time and effort spent on their implementation, and on the other to optimize the transactions themselves, taking into account the possibilities of obtaining general information about the supply and demand of various goods. Thus, spatial localization of market transactions turns out to be the downside of the lack of effective alternative sources of obtaining and exchanging information.

If we take into account the inevitability of significant transaction costs accompanying the process of perfect competition12, then the final result will look different. In this realistic case, competition will not “go all the way”, it will not be able to become “perfect” in the full sense of the word:

without excluding the exchange at non-equilibrium exchange values, it will only narrow their spread in individual transactions.

But this means that reaching the end of the path from the initial distribution of goods to the contract surface will not be made in a “one jump”, but in a multi-stage trajectory, the movement along which is accompanied by a change in the proportions of exchange and distribution of goods between economic agents. Due to the above reasons, the “destination” will necessarily be characterized by a general equilibrium, but the number of such states for any initial distribution of goods will be infinitely large.

In this regard, it makes sense to return to the question outlined above, concerning the number of general equilibrium states. The above-mentioned conclusion, according to which there is a finite odd number of such states in the regular economy, caused disappointment in a certain part of researchers who share the approach to economic theory as an empirical science, in a paradigm based on the concept of general equilibrium. At the same time, the following circumstance caused particular displeasure. The general equilibrium model does not make it possible to formulate so-called “refutable hypotheses” regarding aggregated market variables, since it allows for the possibility of almost any combination of value and natural aggregated indicators and directly opposite reactions of some aggregated indicators to changes in the magnitude of others. Accordingly, the theory loses its “empirical content”. It is for this reason that A. Mas-Colell, M. Whinston and J. Green characterized the Sonnenschein-Mantel-Debreu theorem as denoting that “anything goes”13. It is clear that the conclusion about an infinite number of states of general equilibrium corresponding to any given distribution of goods can be viewed from this position as an additional confirmation of the failure of the paradigm based on the concept of general equilibrium.

However, from the standpoint of “pure economic theory” such a conclusion cannot be accepted. The value of the concept of general equilibrium is in no way belittled by the absence of its property of uniqueness for a given initial distribution of resources between economic agents. If a transition from the initial state to an infinitely large number of points of general equilibrium is possible, then this is nothing more than a feature of the object being studied, but not a defect of the theory describing it. At the same time, to understand how an exchange-based economic system functions, it is fundamentally important to conclude that in all cases it will strive for a Pareto-efficient state of general equilibrium.

About a pure trans-temporal exchange

The analysis of the model under consideration also makes it possible to identify the foundations of credit relations, which are a trans-temporal form of exchange. This problem is investigated in detail in [23]; here we present the main result of our work and make an important clarification regarding one of the conclusions made.

It turns out that with the rejection of the hypothesis of time preference [24; 25], which does not meet the requirement of consistency of the trans-temporal utility function [26], but with the standard assumption that an individual function of trans-temporal utility has the property of a decreasing marginal rate of substitution of the present with the future, the emergence of inkind credit relations becomes possible due to the existence of a special category of goods – durable consumer goods. This conclusion seems to be fundamentally new and important.

The specific feature of durable goods is that they have two exchange values: the exchange value of current services (“rental exchange value”), and the exchange value of the flow of services provided over the entire period of their existence (“commodity exchange value”). These exchange values are realized in two different forms providing for consumer access to such goods through exchange: lease14 and acquisition of ownership.

In an equilibrium situation, the rental exchange value of current services of a capital good is proportional to their marginal utility. In this respect, the formation of demand and supply for the lease of such goods is no different from the formation of demand and supply for “ordinary” (non-durable) goods. It also turns out that the transfer to the ownership of the consumer of a “capital good” is possible not only on the basis of the trade we are accustomed to, but also with the help of credit relations.

For both sides of the transaction, the following two options are equivalent: renting the corresponding good for the entire period of its life and providing it to the consumer, on the condition that the latter carries out loan deliveries during this entire period in an amount corresponding to the value of the rental exchange value. In other words, credit turns out to be a complete substitute for rent in this case.

We should note that although such a loan ensures the transfer of the “capital good” into the ownership of the borrower, it does not require the presence of a commodity exchange value for the object of these relations, as well as the existence of an interest rate. The very durable good is provided on credit (or attracted with the help of a loan); its repayment can be carried out by a counter-good or any other ordinary commodity. In the total amount of loan repayment deliveries, we cannot single out a component that ensures that the lender receives the main part of the debt, on the one hand and interest “income” on the other.

But without the formation of the commodity exchange value of consumer goods of durable use and the interest rate on the market, conditions cannot arise under which a loan would be provided in the form of ordinary goods: it is simply impossible to formulate the terms of such a loan without having the appropriate information. A natural question arises: are there necessary conditions in the pure exchange economy for the formation of the commodity exchange value of consumer durable goods and/or the interest rate?

Let us suppose that such conditions exist. Then the well-known functional relationship between the equilibrium levels of rental exchange value, interest rate and commodity exchange value of “capital goods” can be represented as follows:

EV_k = EV^S ,           (21)

where EV_k is the market exchange value of the capital consumer good, EV_k is the exchange value of the services of this good for one period, ZT   1

(1 + . is the sum of discounts for Tperiods (r is the interest rate for the period, t is the period number). If this equality is violated, one of the forms of attracting capital consumer goods – rent or acquisition of ownership – becomes more beneficial, which indicates the imbalance of the current situation.

The rental exchange value EVk in equilibrium conditions is exactly equal to the current marginal utility of the durable good expressed in terms of the exchange value of the counter-good. Therefore, the commodity exchange value EVk of this good and the value of the interest rate are in a “rigid functional coupling”: it is impossible to determine the equilibrium value of one without simultaneously determining the equilibrium value of the other. But then the question arises, which of these parameters is the leading one: the commodity exchange value of the “capital good” or the interest rate?

As for the question formulated above, it seems to me that it is simply impossible to answer it at this stage of the study. The prospect of finding the answer arises in connection with the transformation of production into an endogenous factor in the model of a simple exchange economy. Looking ahead, I note that such a statement is connected with the confidence that identifying the role of production costs as a factor in the formation of the exchange value of goods will show that in the coupling “commodity exchange value of durable goods – interest rate”, the first of these parameters plays a leading role. In the meantime, we can only state that when studying the pure trade model, it is possible to demonstrate the existence of prerequisites for the simplest form of credit relations. Within its framework, only durable goods can be the object of a loan, and it is impossible to single out “an interest component” in loan servicing supplies.

Conclusions

The well-known model of pure trade harmoniously fits into the logic of general economic theory. Based on the patterns of behavior of an isolated economic agent, which are the object of study at the first stage of analysis, this model allows us to identify possibilities of increasing the level of welfare of at least one of the participants in the redistribution of existing goods without reducing the levels of utility of the remaining members of society. We clearly see the reason that motivates economic agents to enter into exchange relations, and thereby the reason for the transformation of the economic system under consideration: from a set of isolated individual natural economies to a system of members of society united by exchange relations. At the same time, there exists an inextricable link between the basic institutions of an exchange economy (primarily the right of private property) and the principle of Pareto efficiency, which defines the boundaries of mutually beneficial exchange.

The article draws attention to the existence of two institutionally different possibilities for the implementation of the exchange effect , each of which leads to one of the distributions of goods located on the contract surface.

The first possibility consists in the exchange of bundles of goods . The composition of such a bundle is determined according to a well-known model in which the welfare of one of the participants is maximized, while the welfare of the other either remains the same or increases within certain permissible limits. The article shows that such a theoretically conceivable organization of exchange cannot be implemented in practice and is essentially non-market: in general, it does not even allow us to introduce the concept of proportions of exchange, and consequently, the exchange values of individual goods.

The second form of redistribution is based on the classical commodity exchange, the object of which is two goods. This method of redistribution of goods between owners, adequate to the market economy, presupposes the existence of proportions of their exchange for each other, which makes it possible to introduce an important concept of exchange value into the analysis. In modern economic theory, there are two approaches to the study of classical commodity exchange: search for equilibrium proportions of exchange proceeding from L. Walras’ studies, which would make it possible to move from the initial distribution of goods to a distribution corresponding to the state of general equilibrium in a “single jump”, and an approach that allows moving toward the contract surface by means of a series of successive commodity exchange transactions using non-equilibrium proportions of exchange.

The article draws attention to the fact that the implementation of the first approach involves the creation of conditions that allow identifying and coordinating (through finding the equilibrium proportions of the exchange) the individual preferences of its participants before the exchange itself . The Walrasian auctioneer model illustrates this idea in a remarkable way, but it is an exclusively theoretical construction. The alternative is to create a perfect competition mechanism within a spatially localized market.

The analysis of two possibilities of directly achieving (with the help of exchange) the state of general equilibrium urges us to study most attentively the problem of system costs (transaction costs – in the particular case of purely market relations) . Being an economic analogue of friction in the physical world, they help to understand the limitations of certain institutional solutions in terms of the achievability of an ideal result. At the same time, it becomes clear that the desire to reduce system costs is a powerful driver of institutional improvement of the economic system.

Transaction costs also play an important role in moving toward the contract surface through a series of exchange transactions using non-equilibrium prices. The article demonstrates the mechanism by which the movement should ideally be completed not just on the contract surface, but also in a state of general equilibrium. At the same time, an infinite number of such states correspond to any initial distribution of goods, which is determined both by the presence of an inevitable zone of uncertainty in the proportion of exchange within each individual transaction, and by the sequence of transactions themselves.

The article concludes that in the system under consideration, the competition of economic agents will lead to a reduction in the spread of the proportions of exchange in individual transactions, but will not be able to eliminate them completely. In this sense, perfect competition turns out to be an unattainable ideal. The fact that in such conditions an infinite number of states of general equilibrium are preserved, corresponding to any initial distribution of benefits between owners, should in no way be disappointing to the researcher, because it is nothing more than a reflection of the real property of the object in the theory.

Finally, the analysis of the “pure exchange economy” allows us to lay the foundations of the theory of credit and interest rate and demonstrate the limitations in this regard.

Summary: the analysis of the pure trade model makes it possible not only to identify the drivers of development of exchange relations, but also to reveal essential features of most of the main phenomena and processes in the sphere of circulation. At the same time, the necessary prerequisites for involvement in the analysis of problems from the production side have been formed.