Функция Дирихле- источник примеров и контрпримеров

Функция Дирихле определяется следующим образом:

Г 1, если х — рациональное чило , (0, если х — иррациональное число .

Заметим, что на графике этой функции между любыми двумя точками с ординатой 1 находится точка с ординатой 0, и между любыми точками с ординатой 0 находится точка с ординатой 1 (следовательно, график функции Дирихле разрывен в каждой точке). Поэтому график этой функции невозможно построить (мы можем представить при помощи пунктира только «наглядное изображение», похожее на график функции Дирихле).

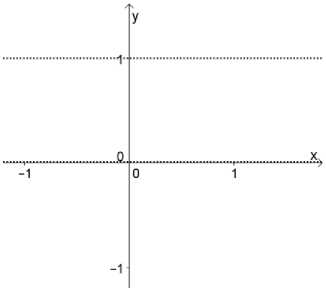
Рис. 1. График функции Дирихле.

Отметим, что функция Дирихле является ограниченной, периодической (её периодом является любое рациональное число) функцией. Кроме того, функцию Дирихле можно рассматривать как источник многих примеров и контрпримеров при изучении математического анализа. Для удобства приведем все предлагаемые примеры в виде таблицы, а затем рассмотрим каждый из примеров.

Предел функции

1. Функция, не имеющая предела в отдельной точке или всюду	f(x)=D(x)
2. Функция,  имеющая  предел только в одной точке	f(x)=x(D(x)- 2 )
3. Функция,  имеющая  предел только при x ^ да	f(x)= 1 (D(x)- 1 )
4. Функции, не имеющие предела ни в одной точке, сумма, разность,   произведение   и частное   которых   имеют пределы в любой точке	D(x)+(-D(x))=0 D(x)-D(x)=0 D(x)D(x+n)=0 D(x) + 1 _ DQx) + 1
5. Всюду         немонотонная ограниченная       функция, имеющая предел	f(x)= 1 (D(x)- 1 ), x>1
6. Немонотонная  ограниченная функция, нигде не имеющая предела	f(x)=D(x)

Непрерывные функции одной переменной

1. Функция,       непрерывная только в одной точке	f(x)=D(x)
2. Всюду разрывные функции, сумма,             разность, произведение   и   частное которых всюду непрерывны	D(x)+(-D(x))=0 D(x)-D(x)=0 D(x)D(x+n)=0 D(x) + 1 D(x) + 1
3. Всюду непрерывная и всюду разрывная         функции, суперпозиция которых всюду непрерывна	Ф<У)= y x f(x)= D(x)- 2 ^(D(x))=(D(x)- 2 ) 2
4. Две    всюду    разрывные функции,      суперпозиция которых всюду непрерывна	ф(у)=в(у) f'(x)=D(x) ф(D(x))=D(D(x))=1
5. Функция,             всюду немонотонная   и   всюду разрывная,        имеющая однозначную      обратную функцию	y=x+D(x) обратная: x=y-D(x)

Рассмотрим теперь непосредственно примеры и контрпримеры.

Как правило, функции из стандартных примеров по математическому анализу имеют пределы в любой точке (например, limx^a sinx существует при любом конечном н) или пределы существуют во всех точках области определения функции, за исключением конечного числа точек (например, у = ~~). Однако существуют функции очень сильно отличающиеся от данных примеров.

Функция, не имеющая предела в любой отдельной точке (поэтому, не имеющая предела всюду).

Непосредственно используя определение предела, можно показать несуществование предела limx^a D(x), где а - любое действительное число. Действительно, пусть г = 0,5. Тогда справедливо высказывание:   найдутся такие значения x1, х2, лежащие в сколь угодно малой окрестности точки а, где х1 -рациональное число, х2 - иррациональное число, что /(х1) — /(х2) = 1 — 0 = 1 > 0,5. А значит, limx^a D(x) не существует.

Функция, имеющая предел только в одной точке.

Рассмотрим определенную на всей числовой оси функцию /(х) = x(D(x) — 0,5). Изобразим график (см. рис. 2) этой функции условно - пунктиром, так как при рациональных и иррациональных значениях х точки графика лежат на прямых у = х/2 и у = —х/2 соответственно.

• •                                   ⁴|^у                                    •

3 2

• -6 -5 -4 -3I ■-2 .Л-- "" (Ь-Д,. 2    3   4    5   6

Рис. 2

Существует lim_x^₀/(х) = 0 как предел произведения бесконечно малой функции / 1 (х) = х на функцию /2 (%) = D (х) — 0,5 - ограниченную, которая принимает только два значения: 0,5 -при рациональных х и —0,5 - при иррациональных х. В любой точке х₀ , отличной от х = 0, функция /(х) не имеет предела, так как в любой окрестности точки х₀ принимает значения как большие х₀/2, так и меньшие — х₀/2.

Функция, имеющая предел только при x ^ + да.

Функция /(х) = | (D(х) — 0,5), х > 1, по той же самой причине имеет предел limx^0 /(х) = 0. Изобразим график (см. рис. 3) функции так же условно – пунктиром. Точки графика функции располагаются при рациональных и иррациональных х соответственно на гиперболах у = 1/(2х) и у = —1/(2х).

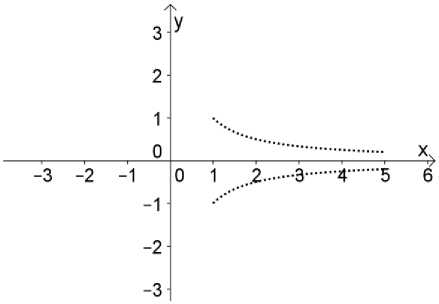
Рис. 3

В любой конечной точке х0 > 1 функция /(х) не имеет предела, так как в любой окрестности точки х0 принимает значения как большие ^|-, так и меньшие

— . 2%0

Известна следующая теорема.

Теорема 1 (о пределе суммы, разности, произведения и частного пределов). Пусть функции /(х) и д (х") заданы в области X с предельной точкой а и при стремлении х к а имеют конечные пределы Птх^а/(х) = А, limx^аg(х) = В, причём д(х^ ^ 0. Тогда и функции /(х)±д(х),  /(х)д(х), ^(-) также имеют конечные gw пределы А±В, АВ, ^ соответственно.

Условие существования конечных пределов lim_x^_a/(х) = А, lim_x^_ag(х) = В функций /(х) и д(х) является достаточным, но не является необходимым. Рассмотрим контрпример.

Функции, не имеющие предела ни в одной точке, сумма, разность, произведение и частное которых имеют пределы в любой точке.

Сумма D(х) + (—D(х)) = 0,  разность D(x) — D(x) = 0, произведение D(х)D(х + л) = 0, частное ^М+А = 1 двух функций, D(x)+1

каждая из которых не имеет предела ни в одной точке, являются константами, т.е. имеют пределы любой точке. Следует только пояснить, что если аргумент х - иррационален, то D(х) = 0, если х -рационален, то х + л - иррациональное число, а значит D(х + л) = 0.

Известна следующая теорема.

Теорема 2 (о пределе монотонной функции). Пусть функция /(х) монотонно возрастает (хотя бы нестрого) в области X, имеющей предельную точку а, и число а (конечное или равное + да) больше всех значений х. Если при этом функция ограничена сверху /(х) < М, для всех х G X, то существует конечный предел limx^a/(x), в противном случае - limx^a/(x) = + да. Аналогичное утверждение имеет место для монотонно убывающей, ограниченной снизу функции.

Монотонность ограниченной функции является достаточным, но не является необходимым условием существования её предела. Приведём контрпример.

Всюду немонотонная ограниченная функция, имеющая предел.

Рассмотренная в примере 1.3 функция /(х) = 1(D(x) — 0,5), х > 1, является ограниченной сверху и снизу, она нигде (ни на каком интервале) не является монотонной. При этом существует предел limx^o/(x) = 0.

Однако условие монотонности нельзя удалить из условий предыдущей теоремы. Рассмотрим соответствующий пример.

Немонотонная ограниченная функция, нигде не имеющая предела.

Простейший пример такой функции - функция Дирихле. Действительно, функция /(х) = D(x') всюду немонотонна и ограничена, так как принимает значения /(х) = 0 или /(х) = 1. При этом мы убедились в примере 1.1, что lim_x^_a D(x) = 0.

Непрерывные функции одной переменной.

Как правило, функции, встречающиеся в типовых задачах по математическому анализу, непрерывны на всей области определения, за исключением, быть моет, только конечного числа точек (например, элементарные функции). Однако такая ситуация не характерна для многих функций

Функция, непрерывная только в одной точке.

Рассмотрим функцию f(x) = xD(x). Функция f(x) определена на всей числовой оси, f(x) = 0 (см. рис. 4).

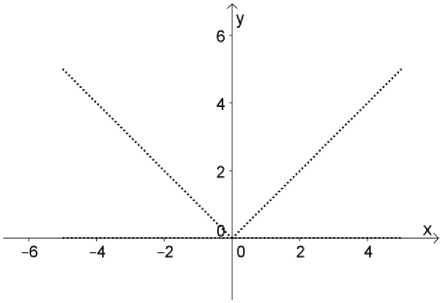
Рис. 4

Покажем, что в точке x₀ = 0 функция f(x) непрерывна. Действительно, lim_x^₀(xD(x)) = 0 как предел произведения бесконечно малой функции на функцию ограниченную и выполняется lim_x^₀ f(x) = f(0). Заметим, что в любой другой точке x 1 ^ 0 функция f(x) разрывна, так как предел lim_X^_Xi f(x) не существует. Это следует из того, что в любой окрестности точки x1 ^ 0 функция f(x) принимает как значения, равные нулю (при иррациональных x), так и значения, большие числа x1 по абсолютной величине (при рациональных x).

Известна следующая теорема.

Теорема 3 (об арифметических операциях над непрерывными функциями). Пусть функции f(x) и g(x) определены на промежутке X и обе непрерывны в точке x0 этого промежутка, причём g(x) ^ 0, тогда в точке x0 будут непрерывны и функции f(x) ± g(x), f(x)s(x), fg..

Условие непрерывности функций f(x) и g(x) в точке x0является  достаточным, но не является необходимым для непрерывности в x0 функций f(x) ± д (x)

f(x)g(x),

У ^(Л)

.

Рассмотрим контрпример.

Всюду разрывные функции, сумма, разность, произведение и частное которых всюду непрерывны.

В данном качестве могут быть рассмотрены функции примера 1.4. Сумма D(x) + (—D(x)) = 0, разность D(x) — D(x) = 0, произведение D(x)D(x + и) = 0, частное ^М+А = 1 двух функций, ¹                    V      х               -             D(x)+1          '                '

каждая из которых разрывна в любой точке числовой оси, являются константами, то есть непрерывны в любой точке.

В курсе математического анализа рассматривается следующая теорема.

Теорема 4 (о суперпозиции непрерывных функций). Рассмотрим функцию р(у), которая определена на промежутке У, и функцию f(x), которая определена на промежутке X, при этом f(x) £ X, если x £ X. Если f(x) непрерывна в точке x₀ £ X, а р(у) непрерывна в точке у₀ = f(x₀), у₀ £ У, то сложная функция p(f(x)) непрерывна в точке x₀.

Условие непрерывности f(x) в точке x0 из X и р(у) в точке y0=f(x0) из У являются достаточными, но не являются необходимыми для непрерывности сложной функции. Рассмотрим контрпримеры.

Всюду непрерывная и всюду разрывная функции, суперпозиция которых всюду непрерывна .

Рассмотрим определенные всюду функции р(у) = у ² и /(х) = D(x) — 0,5. Первая из них всюду непрерывна, вторая - всюду разрывна. Однако сложная функция р(/(х')') = (D(х) — 0,5)2 = 1 непрерывна всюду

Две всюду разрывные функции, суперпозиция которых всюду непрерывна.

Пусть р(у) = D (у), а /(х) = D(х). Эти функции всюду определены и всюду разрывны. Сложная функция р(/(х)) = D (D (х) = 1 всюду непрерывна.

Теперь рассмотрим следующую теорему.

Теорема 5 (о существовании обратной функции). Пусть функция у = /(х) определена, строго монотонно возрастает (убывает) и непрерывна на некотором промежутке X. Тогда в промежутке У значений этой функции существует однозначная обратная функция х = д(у), также строго монотонно возрастающая (убывающая) и непрерывная.

Заметим, что для существования однозначной обратной функции предположения данной теорем являются достаточными, но не являются необходимыми. Рассмотрим пример.

Функция, всюду немонотонная и всюду разрывная, имеющая однозначную обратную функцию.

Определенная на всей оси Ох функция у = х + D (х) ни в одном интервале не является монотонной, она разрывна в каждой точке. Изобразим график схематично – пунктиром.

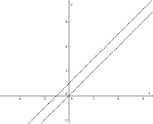
Рис. 5

При иррациональных х точка графика лежит на прямой у = х, при рациональных х - лежит на прямой у = х + 1. Функция имеет однозначную обратную функцию, определенную на всей оси Оу. Действительно, если х - иррациональное число, то у = х, и у также иррационально; если х - рациональное число, то у = х + 1, и у это также число рациональное. Таким образом, рациональным значениям аргумента отвечают рациональные значения функции, и на множестве рациональных чисел существует однозначная обратная функция х = у — 1. Иррациональным значениям аргумента отвечают иррациональные значения функции, и на множестве иррациональных чисел существует однозначная обратная функция х = у. Следовательно, на всей оси Оу существует однозначная функция, обратная функции у = х + D (х). Нетрудно заметить, что она выразится в виде х = у — D(У).

В заключение стоит отметить, что функция Дирихле может служить основой для построения примеров и контрпримеров при изучении основ математического анализа.