Функция восстановления и оптимизация стратегий эксплуатации технических систем при наработках, распределенных как смесь распределений
Автор: Вайнштейн И.И., Федотова И.М., Вайнштейн Ю.В., Цибульский Г.М.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 1 т.18, 2017 года.
Бесплатный доступ
Рассматриваются три характерные задачи математической теории надежности восстанавливаемых технических систем. Это выбор функции распределения наработок элементов до отказа в процессе восстановления, нахождение функции восстановления и определение оптимальной стратегии эксплуатации по критерию минимума интенсивности эксплуатационных затрат. Для многих классических законов распределения, например экспоненциального, Вейбулла-Гнеденко, Эрланга, гамма-распределения, нормального, усеченного нормального, логарифмически нормального, обратного гауссовского, Релея, эти задач хорошо исследованы, Вместе с тем эти законы не могут описать разнообразие распределений наработок элементов технических систем при их эксплуатации. Например, плотности вероятности перечисленных законов не более чем одномодальны, хотя у наработок плотности могут быть бимодальными (двугорбыми) и даже полимодальными, или когда функция распределения наработки до отказа является смесью двух или большего числа функций распределения из множества известных законов распределений. В связи с этим перечисленные задачи изучаются для случая, когда наработки распределены в виде смеси функций распределений. Особое внимание уделено смеси экспоненциальных распределений. Это объясняется тем, что у интенсивности отказов такой смеси имеется период приработки, который характерен для начального периода эксплуатации многих технических систем, после которого интенсивность отказов почти постоянна. Это ее важное отличие от широко применяемого в теории надежности экспоненциального распределения, у которого интенсивность отказов постоянна, а период приработки отсутствует. Для простого процесса восстановления в явном виде получены функции восстановления (математическое ожидание числа отказов на промежутке от нуля до ) для смесей двух экспоненциальных и двух нормальных распределений. Для общего процесса, когда первая функция распределения наработки - смесь , а вторая и следующие - смесь двух экспоненциальных распределений, также получена в явном виде функция восстановления. Для трех стратегий эксплуатации технических систем (в двух из них наряду с аварийными проводятся профилактические восстановления) при наработках, распределенных как смесь экспоненциальных распределений, рассмотрена задача выбора оптимальной по критерию минимума интенсивности эксплуатационных затрат. Методом моментов получены явные формулы точечных оценок трех параметров, входящих в смесь двух распределений Эрланга порядка
Функция распределения, смесь функций распределений, процесс и стратегии восстановления, интенсивность эксплуатационных затрат
Короткий адрес: https://sciup.org/148177673
IDR: 148177673 | УДК: 62-192:621
Текст научной статьи Функция восстановления и оптимизация стратегий эксплуатации технических систем при наработках, распределенных как смесь распределений
Введение. В теории надежности технических систем первичными понятиями являются случайная наработка (время, расстояние) элемента (системы) до отказа и ее функция распределения. Именно они задают важнейшее понятие в теории надежности -процесс восстановления.
Простым (обычным) процессом восстановления называется последовательность неотрицательных взаимно независимых случайных величин X, - наработок элементов от ( i - 1)-го до i -го отказа, имеющих одну и ту же функцию распределения F 1( t ). Если F ( t ) = F 2 ( t ) при i > 2, то имеем общий (запаздывающий) процесс восстановления [1-7].
Стратегии эксплуатации технических систем - это процессы восстановления, учитывающие различные состояния системы, например, аварийные и профилактические восстановления, время и стоимость их проведения [1-13]. Время и стоимость проведения профилактических восстановлений - важнейшие параметры для обеспечения оптимальных показателей надежности и эффективности работы технических систем. Например, минимум интенсивности эксплуатационных затрат, максимум коэффициента готовности.
Так, при эксплуатации ракетно-космической техники, электронно-вычислительных систем, систем электроснабжения, теплоснабжения, транспортных систем и многих других требуется близкий к единице коэффициент готовности, так как отказы и время простоя могут приводить к различным техническим, экологическим, экономическим последствиям. В связи с этим выбор для элементов технических систем верного закона распределения их наработок до отказа, задающего процесс восстановления, выбор оптимальной стратегии восстановления - важнейшие задачи при эксплуатации технических систем.
В теории надежности имеется большое количество классических законов распределения, которым под- чиняются наработки многих элементов различных технических систем, например, экспоненциальное, Вейбулла-Гнеденко, Эрланга, гамма-распределение, нормальное, усеченное нормальное, логарифмически нормальное, обратное гауссовское, Релея, Максвелла [2]. Конечно, все они не могут описать разнообразие распределений наработок элементов технических систем при их эксплуатации. Например, плотности вероятности известных законов не более чем одномодальны, хотя у наработок плотности могут быть бимодальными (двугорбыми) и даже полимодальными, или когда функция распределения наработки до отказа является смесью двух или большего числа функций распределения из множества известных законов распределений.
В связи с этим в работе изучаются процессы и стратегии эксплуатации технических систем для случая, когда наработки распределены в виде смеси функций распределений. Особое внимание уделено смеси экспоненциальных распределений. Это объясняется тем, что у интенсивности отказов такой смеси имеется период приработки, который характерен для начального периода эксплуатации многих технических систем, после которого интенсивность отказов почти постоянна. Это ее важное отличие от широко применяемого в теории надежности экспоненциального распределения, у которого интенсивность отказов постоянна, а период приработки отсутствует.
Постановка задачи. Смесь функций распределений F(t), I = 1,..., n, определяется по формуле nn
F ( t ) = Ё^ ( t ), Xt> 0, £ X Z =1.
i =1 i =1
В работе рассматриваются три задачи:
-
1. Нахождение функции восстановления (среднего числа отказов на промежутке от нуля до t ) для процесса восстановления, образованного смесью функций распределения.
-
2. Сравнение трех стратегий эксплуатации технических систем (стратегии только аварийных восстановлений, стратегии замен блоками и периодической стратегии восстановления) по критерию минимума интенсивности затрат, когда наработки элементов после аварийных и профилактических восстановлений распределены как смесь функций распределения.
-
3. Нахождение методом моментов точечных оценок неизвестных параметров, входящих в смесь двух распределений Эрланга порядка n .
Смесь экспоненциальных распределений. Рассмотрим смесь экспоненциальных распределений nn
F ( t ) = ^ Х , (1 - e -ait ) = 1 - ^ e^t . i =1 i =1
Характеристики смеси экспоненциальных распределений:
тонно убывая, стремится к нулю при t , стремящемся к бесконечности. Характерный график плотности экспоненциальных распределений имеет вид, представленный на рис. 1.
Исследуем функцию интенсивности отказов:
limX( t) = lim t ^x t ^x
n
EX i ae i=1
n j X i e - i =1
n
X k a k + j X e -,a.-a - =1, i У k _ _
-
- lim-------- n --a k , a k = min a i , t "” X k + j X e -(ai-ak ) t ' = 1,2, ... , П
i =1, i Ф k
n f (t) = jXiaie ai - плотность, i=1
X ( t ) =
f ( t )
1 — F ( t )
n j ia ie i=1
n jXe^
i =1
- интенсивность отка-
nn n
- j Xa 2 e -a^ j X e -a^ +| j X i a i e -ai‘ i =1 i =1 V i =1
зов,
n
E -a. t
X e i I
E(X) = jX,h„ ^-= E(Xi) = —, i=1
D(X) = jXD, Di= D(Xi) =4. i=1
Имеем
nn f (t) = -jXia2e-at < 0, f"(t) = jXia3e~a/t > 0, i=1
n
f(0) = jX№>0, limf (t) = 0. i=1
Отсюда следует, что функция плотности смеси экспоненциальных распределений вогнута и, моно- nn j j XiXj(«i-«j)2e-(ai+aj)t
_ i =1 j =1, j ^ i ^^™^^™ ^^^^^^* ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
( n 3 2
-
2 X, e -a li
i
V i =1 )
n
X (0) = j X i « i > 0.
i =1
Получили, что функция интенсивности отказов монотонно убывает, и прямая X = a k является ее горизонтальной асимптотой. Характерный график функции интенсивности отказов имеет вид, представленный на рис. 2.
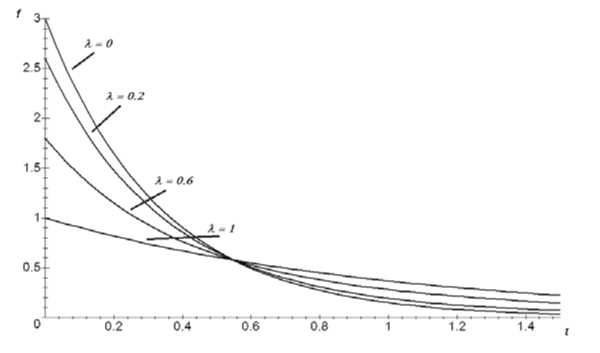
Рис. 1. Графики плотности экспоненциальных распределений f ( t , X , a 1, a 2) = Xa 1 e a t + (1 -X ) a 2 e a 2 t при a 1 =1, a 2 = 3
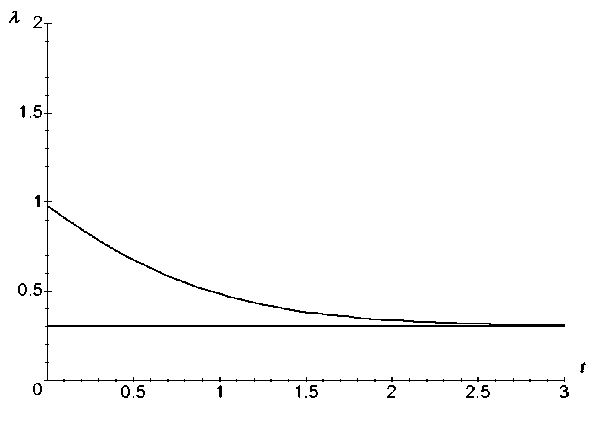
Рис. 2. Интенсивность отказов смеси при n = 2, X 1 = 0,4, X 2 = 0,6, a t = 2, a 2 = 0,3
Замечание . Интенсивность отказов экспоненциального распределения постоянна ( X ( t ) = a ). Из рис. 2 видно, что интенсивность отказов смеси экспоненциальных распределений имеет период приработочных отказов, и лишь с увеличением продолжительности работы интенсивность становится практически постоянной. Это существенно отличает смесь экспоненциальных распределений от одного экспоненциального распределения, у которого интенсивность отказов не имеет периода приработки, такого важного и характерного в начальный период работы многих технических систем.
Функция восстановления процесса восстановления, образованного смесью функций распределений. Функция восстановления H ( t ) (математическое ожидание числа восстановлений N ( t ) за время от нуля до t ) определяется по формуле [1-7]
X
H ( t ) = E ( N ( t )) = £ F ( n ) ( t ), (1)
n =1
где F ( n ) ( t ) - n -кратная свертка функций распределения, задающих процесс восстановления:
F ( n ) ( t ) = ( F ( n - 1) ■ Fn )( t ), F (1)( t ) = t
= F ( t ),( F ■ F 2)( t ) = J F( t - x ) dF 2 (x ).
Рассмотрим смесь двух распределений
F
(
t
)=
X
F
(
t
)
+
(1
-X
)
F
2(
t
), 0
Формула (1) с использованием формулы бинома Ньютона запишется в виде
X X
H ( t ) = £ F ( n ) ( t ) = £ ( X F ( t ) + (1 - X ) F ( t ))( n ) ( t ) = n =1 n =1
X n
= ££ c n X n - k (1 -X ) k ( f ( n - k ) ■ F k ) )( t ), n =1 k =0
C k = n !
n k !( n - k )!
- количество сочетаний из n эле- ментов по k, (F(n) ■ F2(0))(t) = F(n)(t).
Получим функцию восстановления простого процесса, образованного смесью двух нормальных распределений:
F ( t ) = XФ f t -B1 + (1 - X ) Ф f t -^ 2 1 ,
I ° 1 J I ^ 2 J
1 t - x
Ф ( t ) = ,— J e 2 dx . а/2л-Х
Учитывая, что сумма двух независимых нормально распределенных случайных величин также распределена по нормальному закону, причем математические ожидания и дисперсии складываются, и что свертка их функций распределения дает распределение суммы этих случайных величин [6], получаем:
F ( n - k ) ( t ) = ф
t - ( n - k ) ц 1
O 1 V n - k
F 2 ( k ) ( t ) = ф| t— k ^ 2 I , ( ^ 2 V k J
F ^( n - k )
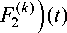
t - (( n - k ) ц 1 + k ц 2)
^ ^a2(n - k) + ^2k ?
После подстановки в формулу (2)
x n h (t ) = ££ Cnk Xn -k (1 -X)k x n=1 k=0
хф t - (( n - k ) P 1 + k Р з )
^ G 2 ( n - k ) + ^ 2 k ?
Замечание . Смесь двух нормальных распределений дает возможность получать двумодальные (двугорбые) распределения (рис. 3).
Обозначим HFG ( t ) функцию восстановления общего процесса, образованного первой функцией распределения F ( t ), а второй и следующими - G ( t ).
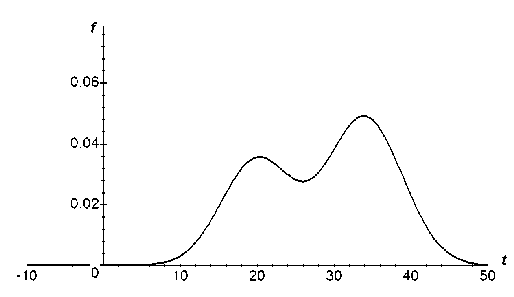
Рис. 3. Плотность смеси двух нормальных распределений при X = 0,4, a = 20, G j = 4,6, а 2 = 34, а 2 = 4,8
Пусть F ( t ) - смесь n экспоненциальных распределений
n
F (t) = ^X(1 - et), i=1
а G ( t ) - смесь двух экспоненциальных распределений
= № 1 +
(1 -Ц ) Р 1 +ЦР 2 s
, ц (1 -Ц )( р 1 -P 2 )2 1
(1 -ц ) Р 1 +цв 2 s + (1 -ц ) Р 1 +цв 2
G ( t ) = ц ( 1 - e 1 t ) + (1 -ц ) ( 1 - e '’ t ) ,
0 <ц< 1.
После обратного преобразования
HG ( t ) =---^--- 1 +
(1 -Ц ) р 1 +Цр 2
Запишем интегральное представление функции восстановления HFG ( t ) через функцию восстановления HG ( t ) простого процесса, образованного функцией распределения G ( t ) [2; 3]:
HFG ( t ) = F ( t ) + J HG ( t - x ) dF ( x ). (4)
Функция восстановления HG ( t ) удовлетворяет интегральному уравнению [2]
HG ( t ) = G ( t ) + J HG ( t - x ) dG ( x ),
+ ц(1-цЖ-р2)!. / ((1 -ц^ +ЦР 2 )2 (
-
e -((1-ц)₽ 1 +ц₽2) t )
В обозначениях
A = Р 1 Р 2 B = Ц (1 -Ц )( в 1 -Р 2 )2 (1 -Ц ) р 1 +Цр 2 , ((1 -Ц ) р 1 +ЦР 2 )2 ,
D = ( 1 -ц ) Р 1 +цв 2 ,
HG ( t ) = At + B (1 - e - Dt ). (6)
которое для рассматриваемого случая принимает следующий вид:
HG ( t ) = ц ( 1 - e -P 1 t ) + (1 - ц ) ( 1 - e 1 ■’ t ) +
V (5)
+ J HG ( t - x ) d ( ц ( 1 - e " x ) + (1 - ц ) ( 1 - e e 2 x ) ) .
Переходя в (5) к преобразованию Лапласа-Стилтьеса
Подставляя найденную HG ( t ) в (4), после интегрирования получаем
Г А DR 1
HFG(t) = At + УХ 1--+----- х f-r I a D-а)
X h - e -“H - B y 2 - ^^(1 - e - Dt ).
( ) и D -a?
да
F * ( 5 ) = J e - st dF ( t ) и учитывая ( 1 - e 0
* * * _. _
( F 1 ■ F 2) ( s ) = F ( s ) F 2 ( s ) [2], получаем
-(
“ t ) * ( s ) = -?- , ' s + a
Положив здесь ц = 1, получим функцию восстановления общего процесса, образованного первой функцией распределения как смесь n экспоненциальных распределений, а второй и следующими - G ( t ) = 1 - e -e t , в = в 1 .
HG * ( s ) =
ЦР 1 + (1 -Ц ) в 2 + HG *( s ) I ЦР 1 + (1 -Ц ) в 2 s + в s + P 2 \ s + в s + P 2
Отсюда:
HFG ( t ) = в t + И X i .I1 - -^ 1 ( 1 - e - ait ) . (7)
7 =7 ( a , Jx '
HG ( s ) =
цв 1 + (1 -ц ) в 2
s + в s + P 2
1 I M0 1 + (1 -ц )вГ ( s + P j s + P 2
( Цр ! + (1 -Ц ) р 2) s + p t p 2 s ( s + (1 -ц ) Р 1 +ЦР 2 )
Оптимизация стратегий восстановления. Рассмотрим три стратегии восстановления, предполагая, что все восстановления происходят за пренебрежимо малое время и система функционирует неограниченно долго (достаточно долго) [2]:
- стратегия Ca - стратегия аварийных восстановлений, проводятся только аварийные восстановления;
- стратегия Cb - стратегия восстановления блоками, наряду с аварийными восстановлениями в фиксированные моменты времени т, 2т . проводятся про филактические восстановления;
- стратегия C- - стратегия строго периодических восстановлений, наряду с аварийными восстановлениями проводятся профилактические, если элемент проработал без отказов заданный интервал времени т.
Интенсивности затрат (средние затраты на восстановления в единицу времени) R a , R b , Rc для стратегий C a , C b , C c вычисляются соответственно по формулам [2]
с cn + caH ( т )
Ra = -a-, Rb (т) = p a 1 ' , Ц2
„ , , -aF(т) + -p (1 - F(т))
R- (т) =-----Т’
J<1 - F (t)) dt где -a, cp - средние затраты на аварийные и профи лактические восстановления соответственно; р, = = E(Xi) - средняя наработка элемента до отказа. Первая формула в (8) дает интенсивность затрат стратегии Ca при аварийных восстановлениях, образующих общий процесс восстановления, вторая - интенсивность затрат стратегии Cb для случая, когда аварийные восстановления образуют общий процесс восстановления, а после каждого профилактического восстановления в моменты времени т, 2т, .., nт заново начинается рассматриваемый общий процесс восстановления. Третья формула в (8) дает интенсивность затрат стратегии Cc, когда функции распределения наработок при всех аварийных и профилактических восстановлениях совпадают.
Рассмотрим стратегию C b при общем процессе восстановления, когда первая функция распределения является смесью n экспоненциальных распределений, а вторая и следующие - экспоненциальное распределение.
Учитывая (7), запишем функцию интенсивности затрат:
- + c H ( т ) R b ( т ) = p a V ’ =
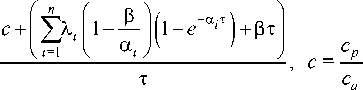
Имеем lim R b ( т ) = х , lim R b ( т ) = - a в . т^0 т^х
Получили формулу R a = c a в - интенсивности эксплуатационных затрат стратегии только аварийных восстановлений C a (время проведения профилактических восстановлений устремляем к бесконечности). Заметим, что прямая R b = c a в = R a является горизонтальной асимптотой графика интенсивности затрат R b ( т ). Далее
R b ( т ) = ca Х
n
Х-М" -в ) e "i i =1
о 1 о fi в ^Л —ад
+ в |т- c -вт- Х Х i 1 1-- 1 ( 1 - e i
) i =1 l a i г
-c-1 + p£ Xi + £Xi[(ai-в)т + (1 -^)] e - iт _____________i=1а i i=1
- caт
Введем функцию (числитель в формуле для R b )
nn f ш-c -1+вХ—+Хх i i =1 аii
( а i - в ) т +[ 1 -— i а i
- а i т
Имеем nn f (0) = -c-1+вХ -+■ Xх i 11— i=1 ai i=1 i
—<
" X, f И = - c -1 + вХ—, i=1 а i nn f,(т) = Xх, (а i-в) e-a iт Xх i ai(a i-в)т e-a iт -i=1
nn
-
- X х i ( a i - в ) e -a i т = т Х х i a i ( в - a ) e -ат .
i =1
Потребуем выполнения двух неравенств f (х) - -c -1 + в]Х ^^ > 0, ]ТXiai (в - ai)e-,т > 0.
i=1а ii
Они выполняются, например, при в> max ai, в >(c +1)/ ХЬ—.(9)
i =1 a i
Тогда функция f ( т ) монотонно возрастает на промежутке (0, х ), и, будучи отрицательной в нуле и положительной на бесконечности, она, а вместе с ней R b , ( т ), один раз пересекает ось O т в некоторой точке т = т * > 0.
Точка т = т * > 0 является точкой минимума функции Rb ( т ), так как при ее переходе функция R'b ( т ) меняет знак с « - » на « + ». Учитывая еще поведение Rb ( т ) в нуле и на бесконечности, заключаем, что в точке т = т * функция интенсивности затрат стратегии Cb принимает наименьшее значение, и Rb ( т * )< Ra , так как если Rb ( т * ) > Ra , то функция Rb ( т ) должна была бы иметь более чем одну точку экстремума.
Таким образом, установили, что по критерию минимума интенсивности затрат при выполнении неравенств (9) следует проводить стратегию Cb в сравнении со стратегией Ca .
Характерные графики интенсивностей затрат стратегий Cb и Ca при выполнении неравенства (9) имеют вид, представленный на рис. 4.
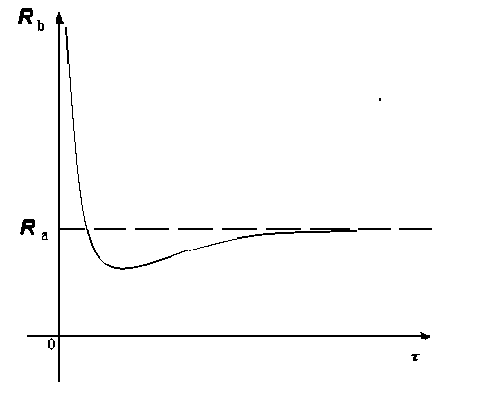
Рис. 4. Графики интенсивностей затрат стратегий C b и Ca
Сравним стратегии C b , Cc со стратегией Ca по критерию минимума интенсивности затрат за счет выбора оптимального времени проведения профилактических восстановлений, когда функции распределе -ния наработок при всех аварийных и профилактических восстановлениях совпадают и являются смесью двух экспоненциальных распределений (3).
Рассмотрим стратегию Cb. Запишем функцию интенсивности затрат:
R b ( т ) =
Cp + ca (Aт + B (1 - e-DT))
1 - (1 - c) (pe в1т + (1 -p)e в2т) pp2 + (1 - p)P1 -(pp2e + (1 - p)P1 e )’ (10)
Далее
R c ( т ) - R a =
= C a P 1 P 2
-
1 - (1 - c ) ( p e P< ■ (1 p i e P;< ) х pp 2 + (1 - p ) P 1 - ( pp 2 e -р1 т + (1 - p ) p 1 e -р2 т )
Из lim Rb (т) = caA следует формула интенсивности т^л затрат стратегии только аварийных восстановлений:
(1 -p ) P 1 +pp 2
Ra = caA = ca P 1 P 2 a a a (1 -p ) P 1 + pP 2
.
Сравним интенсивности затрат стратегий Cb и Ca :
R b ( т ) =
C p + C a ( A т + B (1 - e - D т ))
т
> C a A = R a .
p(p2 - k(1 - c))e в1т + oo + (1 -p)(p1 - k (1 - c)) e-р2т e1e2 -в -ex ,
(k-(p₽2 e P1 + (1 -p)e1e 02 )) k k = (1 -p)P1 +pp2.
Отсюда Rb ( т ) > Ra .
Таким образом, в рассматриваемом случае, в сравнении со стратегией Ca , стратегию Cb проводить нецелесообразно. Профилактические восстановления лишь увеличат интенсивность затрат.
Рассмотрим стратегию Cc :
C a ( p (1 - e -Р * т ) + (1 -p )(1 - e -в 2 т )) + + C p ( p e P< ■ (1 -p ) e P<) J> e '" t + (1 -p ) e P ’ t ) dt
Ca (p(1-e Р‘т) + (1 -P)(1-e Р2т)) +
+ C p ( p e P< ■ (1 -p ) e ’ т )
(1 - e P< ) ■ 1-^(1 - e P<)
P1( ) P2 ( )
Пусть P 2 > P 1 . Отсюда e р 1 т > e р 2 т при т >0.
Рассмотрим числитель в (11):
p ( p 2 -(1 (1 - c )) e" р 1 т + (1 -p )( P 1 - k (1 - c )) e р 2 т .
Покажем, что P 2 - к (1 - c ) > 0 . Имеем:
P 2 - к (1 - C ) = к I C - 1 + P 2 1 = х к J
1 Г , P2 - pP2 - (1 -p)P1 ) = к c += х к J
= к I c + ^1^)( P2ZP1)) >0. х к J
Учитывая еще, что e P^ > e ^, покажем, что числитель в (11) больше нуля:
p ( P 2 - к (1 - c )) e ^ + (1 -p )( P 1 - к (1 - c )) e ^ >
> e "^ № - k (1 - c )) +
+ (1 - ц )( Р 1 - k (1 - c ))) = e e ' T kc > 0.
Аналогично показывается, что и при Р 2< Р 1 числитель в (11) больше нуля.
Из вида формулы (10) следует, что ее знаменатель больше нуля. Таким образом, у выражения Rc ( t ) - R a при т >0 числитель и знаменатель положительны. Следовательно, при всех т >0
R c ( T )> R a .
Таким образом, установили, что в случае простого процесса восстановления со смесью двух экспоненциальных распределений (3), при выборе из стратегий C a , C b , Cc оптимальной по критерию минимума интенсивности эксплуатационных затрат, оптимальна стратегия C a - стратегия только аварийных восстановлений.
Замечание . Рассмотрение стратегии C b при общем процессе восстановления, когда первая функция распределения является смесью n экспоненциальных распределений, а вторая и следующие - одно экспоненциальное распределение, показало влияние распределения наработки до отказа первого заменяемого элемента в процессе восстановления. Так, при выполнении неравенства (9) по критерию минимума интенсивности эксплуатационных затрат следует проводить стратегию Cb с профилактикой в моменты времени т * , 2 т * ... в сравнении со стратегией C a , в которой профилактические восстановления не проводятся.
Метод моментов получения точечных оценок неизвестных параметров смеси двух распределений Эрланга порядка п. Рассмотрим метод моментов нахождения точечных оценок параметров смеси распределений, так как нахождение точечных оценок методом максимального правдоподобия для смеси распределений значительно усложняется. Это связано со сложностью трансцендентной целевой функции правдоподобия для минимизации и большим количеством неизвестных параметров (к параметрам функций распределения, задающих смесь, добавляются неизвестные параметры Xi с дополнительными усло-k виями Xj > 0, ^Xi = 1). Задача может усложниться за i=1
счет определения функций распределения, задающих смесь, и их количества. Это так называемая задача расщепления смеси. В работах [14-16] рассматривается теория и алгоритмы решения таких задач методом максимального правдоподобия. Заметим, что оценки, полученные методом моментов, могут являться начальным приближением при решении задач методом максимального правдоподобия.
Пусть F(t, а1, а2, ..., аr) - функция распределения, а1, а2, ..., аr - неизвестные параметры. Методом моментов точечные оценки параметров а1, а2, ..., аr находятся, приравнивая теоретические моменты да рk = Jxk dF(x,а1,а2, ...,аr) и
N
Mk = N / x до порядка r :
эмпирические моменты
да k .1
J x dF ( x , а 1 , а 2, ..., а r )- —
0 N
Z X , k = 1... r . (12)
Рассмотрим смесь двух распределений Эрланга порядка n
F ( t ) = X| 1 - e а 1 tn -1< а 1 £ ) I
V i =0 k !
+
+ (1 -X )f1 - e а 2 t V ( а 2 t ) T а! ^ а2 , | I" 1 2
V i=0 k! J f (t) = X(а1) t eа1 + (1 -X) (n -1)!
(а2) n t n -1 а2 1
--------------e 2 .
( n - 1)!
При n = 1 имеем смесь двух распределений.
Методом моментов получим экспоненциальных
точечные оценки
параметров а1, а2, X (n - задано). С использованием да формулы J tke
-<
а t. к !
t dt---—г , в соответствии с (12)
а к+ получаем систему для определения а1, а2, X :
n X n (1 -X) ,,
+ а1
n(n +1)X + n(n+1)(1 -X) = M а2 а2'
n ( n + 1)( n + 2) X n ( n + 1)( n + 2)(1 - X ) _
3 + 3 M 3 .
а1
В переменных Р1 =—, Р2 =— систему (13) запи-а1
шем в виде
XP 1 + (1 -X ) P 2= M 1 , M 1 = M 1, n
XP2 + (1 -X)P2= M 2, M 2= -M2-,(14)
n ( n + 1)
XP 3 + (1 -X ) P 2 = M 3 ,
M 3 =
M 3 n ( n + 1)( n + 2)
Из системы (14) исключаем X: X =
M 1 -p 2
P 1 -₽ 2 ’
M 1(P1 +P2)-P1P2= M 2,(15)
M 1 ( P 1 +P 2 )2 - M 1 P 1 P 2 -P 1 P 2( P 1 +P 2 ) = M 3 .
В переменных p = Р 1 +P 2 и q = P 1 P 2 система (15) переходит в систему двух линейных уравнений относительно p и q
M 1 p - q = M 2 , M 2 p - M 1 q = M 3 .
и
Отсюда
M 3 - M 1 M 2 p =2
M 2 - M 1
M 1 M 3 - M 2 q =2
M 2 - M 1
p + p
,
β 2 = p
-
.
Возвращаясь к неизвестным решение системы (13):
α 1 , α 2 , запишем
λ=
( M 1 α 2 - 1) α 1
,
α 2
-
α 1
α1= p+
α 2 = p
-
Замечание . Если для конкретной выборки найденные решения α 1 , α 2 комплексные, или хотя бы одно из них неположительное, или найденное λ не удовлетворяет неравенству 0 ≤λ≤ 1, то метод моментов для данной выборки не дает возможность получить точечные оценки для параметров α 1 , α 2 , λ .
Из формул (16) при n =1 получаем оценки параметров α 1 , α 2 , λ для смеси двух экспоненциальных распределений:
λ = ( M 1 α 2 - 1) α 1 α 2 λ =, α 1 = ,
α 2 -α 1 p + p 2 - 4 q
2 α2 = 2, p-p2 -4q
= M 3 - 3 M 1 M 2 = 2 M 1 M 3 - 3 M 2 2 p 3( M 2 - 2 M 12) , q 6( M 2 - 2 M 12) .
Заключение. Экспоненциальное распределение широко применяется в теории надежности технических систем. В периоде нормальной работы технических систем, когда на надежность влияют в основном внешние воздействия, интенсивность отказов имеет почти постоянный характер. Это позволяет при решении теоретических и ряда практических задач принимать у наработок до отказа экспоненциальное распределение – у экспоненциального распределения интенсивность отказов постоянна. Решения многих задач выписываются в явном виде. Отсутствие у интенсивности отказов экспоненциального распределения периода приработки и старения существенно обедняет использование экспоненциального распределения в прикладных задачах надежности технических систем.
У смеси экспоненциальных распределений, рассмотренной в работе, интенсивность отказов убывает, имеется период приработки, и она быстро становится почти постоянной. Такая смесь распределений принадлежит к классу распределений с монотонно убывающими интенсивностями отказов. Этому классу, например, принадлежат важные в теории надежности распределение Вейбулла–Гнеденко и гамма-распределение при значениях параметра формы, меньших единицы.
Проведенное исследование триады задач – нахождение в явном виде точечных оценок параметров смеси методом моментов, функции восстановления при простом и общем процессах восстановления, выбор оптимальной стратегии эксплуатации, обосновывает дальнейшее исследование теоретических и прикладных задач со смесями многих распределений в теории надежности технических систем.
Список литературы Функция восстановления и оптимизация стратегий эксплуатации технических систем при наработках, распределенных как смесь распределений
- Smith W. L. Renewal theory and its ramifications//J. Roy. Statist. Soc. 1958. Ser. B 20. Р. 243-302.
- Байхельт Ф., Франкен П. Надежность и техническое обслуживание. Математический подход: пер. с нем. М.: Радио и связь, 1988. 392 с.
- Вопросы математической надежности/Ю. К Беляев . М.: Радио и связь, 1983. 376 с.
- Барлоу Р., Прошан Ф. Математическая теория надежности: пер. с англ. М.: Сов. радио, 1969. 488 с.
- Булинская Е. В., Соколова А. И. Асимптотическое поведение некоторых стохастических систем хранения//Современные проблемы математики и механики. 2015. Т. 10, № 3. С. 37-62.
- Гнеденко Б. В. Курс теории вероятностей. М.: Наука, 1988. 446 с.
- Кокс Д., Смит Д. Теория восстановления: пер. с анг. М.: Сов. радио. 1967. 292 с.
- Vainshtein I. I., Mikhal’chenko G. E., Vainshtein V. I. Optimizing the replacement order to minimize the mean number of system faults//Journal of Machinery Manufacture and Reliability. 2012. vol. 41, iss. 5. P. 417-421.
- Вайнштейн В. И. Математическое и программное обеспечение оптимизации проведения профилактических восстановлений при эксплуатации электронно-вычислительных систем: автореф. дис. … канд. физ.-мат. наук. Красноярск, 2006. 22 с.
- О выборе стратегий эксплуатации технических систем/И. И. Вайнштейн //Вестник СибГАУ. 2015. № 3 (16). С. 645-650.
- Оптимизация стратегий эксплуатации технических систем с проведением аварийных и профилактических восстановлений/И. И. Вайнштейн //Вестник СибГАУ. 2014. № 2 (54). С. 20-25.
- Каштанов В. А., Медведев А. И. Теория надежности сложных систем. М.: Физматлит, 2010. 606 с.
- Надежность технических систем/Е. В. Сугак ; НИИ СУВПТ. Красноярск: МГП «Раско», 2001. 608 с.
- Прикладная статистика. Классификация и снижение размерности/С. А. Айвазян . М.: Финансы и статистика, 1989. 607 c.
- Батракова Д. А., Королев В. Ю. Вероятностно-статистический анализ хаотических потоков в телекоммуникационных сетях с помощью скользящего разделения смесей//Системы и средства передачи информации. Специальный выпуск. М.: ИПИ РАН, 2006. С. 183-209.
- Королев В. Ю. ЕМ-алгоритм, его модификации и их применение к задаче разделения смесей вероятностных распределений. Теоретический обзор. М.: ИПИ РАН, 2007. С. 94.


