Функционал ожидаемой полезности: принципы моделирования и практического применения

Конвергенция теорий риска и ожидаемой полезности с теориями знаний и сложных систем (СС) открывает возможности расширенного применения новых информационных технологий в практических целях [1-3]. Под конвергенцией (от лат. convergere – приближаться, сходиться) будем понимать развитие указанных теорий по пути сближения и приобретения общих или сходных признаков; примером новых информационных технологий является метод статистического имитационного моделирования (СИМ) по версии Димова-Маслова (МДМ) [4-5], включающий методы сценариев и функционально-стоимостного анализ [6], а также использующий компьютерную технологию метода Монте-Карло (ММК). Стимулом для указанной конвергенции являются синергетические эффекты, многократно увеличивающие ценность перечисленных СС знаний.

В практическом плане версия МДМ ориентирована на повышение эффективности функционирования СС путем оперативного управления ее характеристиками [1-4]. Цель статьи – анализ критериев, предназначенных для использования при управлении СС организационно-технического типа, которые могут быть получены в рамках теорий риска и ожидаемой полезности.

Область применения теорий риска и ожидаемой полезности

В приложениях теорий риска и ожидаемой полезности для оценки неопределенности используются «линейные» критерии риска типа – вероятность результата А работы СС ; А_S – его полезность (стоимость рискового выигрыша или проигрыша, в денежных или любых других единицах). Если воспользоваться методом сценариев [6], то можно просчитать значения А_S для каждого сценария с помощью метода функционально-стоимостного анализа

(по максимуму, по минимуму, в среднем), а также дать оценку вероятности реализации каждого сценария P ( A ) при помощи интерсубъективных экспертных методов, отражающих согласованное предпочтение (групповое мнение) лиц, принимающих решения (ЛПР) в рамках принятой онтологической модели ситуации (ОМС) [7].

Отметим, что неопределенность не означает отсутствие информации об СС – речь идет о неполноте, неточности, неадекватности имеющихся сведений [8]. Механизм уменьшения этой неопределенности может быть линейным, нелинейным, аддитивным, синергетическим – чтобы правильно воспользоваться им, нужно знать специфику каждой рассматриваемой СС, а также учитывать субъективный «человеческий фактор». Последнее объясняется тем, что роль личности при проведении такого рода исследований достаточно велика. Это касается и методики сбора и обработки первичной информации, и выбора способов представления и критериев оценки конечных данных, и тем более – форм их последующего применения. Но если полученные данные остаются неопределенными по своей физической сути, использовать их в точных математических формулах все равно бесполезно – это будут «обман и пустая трата времени» [9].

Поэтому СИМ по МДМ уделяет особое внимание особенностям поведения ЛПР (менеджеров, операторов, клиентов, партнеров, конкурентов и т.п.) корпорации. Принимаемые решения считаются результатом упорядоченного (поддающегося структурированию и формализации) процесса мышления разумных людей, априори вводятся предположения о характере их действий в виде аксиом рационального поведения.

На основе указанных аксиом (наиболее важными из них являются аксиомы транзитивности, безразличия, независимости и рациональности) Дж. фон Нейманом и О. Моргенштерном в 1947 г. была сформулирована и доказана теорема о су- ществовании функции полезности, определяющей действия ЛПР [10]. Полезностью при этом была названа некая условная (воображаемая) величина, которую в процессе выбора максимизируют ЛПР с упомянутым рациональным мышлением – своего рода мера психологической и потребительской ценности для них различного рода реальных и виртуальных благ.

Теория объективной ожидаемой полезности предполагает, что в процессе принятия решений рационально мыслящий ЛПР «взвешивает» различные альтернативы и выбирает из них ту, полезность которой максимальна. Функционал объективной полезности (ФОП) фон Неймана-Моргенштерна для N -мерной альтернативы имеет вид

N

^FN=^P_n Q„ , (1)

n = 1

где p – вероятность n -го возможного результата, имеющего для ЛПР объективную ценность (стоимость) Qn ’ n [1; N ]. Считается, что рациональный человек при выборе решения должен руководствоваться правилом f_n = max .

Однако почти одновременно Л. Сэвиджем было предложено правило, положившее начало теории субъективной ожидаемой полезности [11], в рамках которой ФОП представляет собой

рмАХЖ, (2)

где P^x_n ) – оценка вероятности n -го возможного результата экспертом X _n ’ которая имеет для него ценность Q^v^n ) • В данном случае разные ЛПР могут делать разный выбор из одинаковых альтернатив, руководствуясь субъективными соображениями (которые зависят от их личных качеств, знаний, опыта, предпочтений, предубеждений и т.п.), причем каждый эксперт вправе руководствоваться собственным правилом F_N(x_n) = MAX , и выработка группового решения требует от ЛПР коллективных усилий в рамках сложившейся ОМС [7].

Если ЛПР договорятся между собой и придут к согласию относительно совместных оценок и правил сотрудничества, то

P(x„) - p_n; Q(x„) - Q„ (3)

и значения обоих ФОП будут одинаковыми. Возможность для этого создает понимание всеми ЛПР, что объективно существуют и управляют их решениями общие для них эвристики (от греч. heurisko – нахожу, в данном случае – совокупности логических приемов и методических правил), которые определяют закономерности отклонения поведения реальных ЛПР от поведения рационального человека.

К числу таких эвристик относятся суждения по представительности, по встречаемости, по точке отсчета, а также «сверхдоверие» личному опыту и стремление исключить риск [11]. В то же время какими-либо конкретными рекомендациями по составу и структуре ФОП теории риска и ожидаемой полезности не располагают – настоящая статья призвана уменьшить этот пробел.

Функционал ожидаемой полезности

Рассмотрим случай, когда приемлемый риск минимизирует потери (затраты) для рассматриваемого объекта (организации, фирмы, физического лица и т.д.), связанные с достижением поставленной цели в корпоративной СС организационно-технического (холонического) типа [6]. Пусть ЛПР S_n , принадлежащий совокупности n [1; N ], рассматривает K вариантов своих действий (сценариев развития событий), направленных на достижение указанной цели как некоего важного для него позитивного эффекта (выигрыша) F_k , который может быть им лично достигнут с вероятностью p_F при затратах, равных G_k , которые могут быть лично им обеспечены с вероятностью p_G . Значение p_F также учитывает меру правильности прогноза S_n получить на выходе проекта по k -му сценарию выигрыш F_k , а значение p_G – шансы ЛПР собрать ресурс G_k , необходимый для начала выполнения проекта.

Субъект S_n также учитывает, что k -ый сценарий приводит к достижению цели не гарантированно, а с вероятностью p_k , которая характеризует некие объективные (зависящие не только от него лично, как внешние, так и внутренние) обстоятельства: например, в виде согласования и утверждения проекта в вышестоящих инстанциях и т.п. Тогда в качестве критерия эффективности k -го сценария ЛПР может быть выбрана расчетная величина

Qk =Pk k -p_G G_k\ (4)

где k [1; K], которая и является в данном случае прогнозируемой и допустимой (по его мнению) мерой риска. В наиболее общем плане – при проведении СИМ по МДМ произвольной СС организационно-технического типа – значение Qk будем считать некоторой конкретной полезностью рассматриваемого проекта: понимая под Fk предпо- лагаемый «доход», а под Gk – «расходы», связанные с реализацией k-го сценария. Тогда, следуя логике и терминологии фон Неймана – Моргенштерна и Сэвиджа, Qk также можно именовать

ФОП, который в данном случае является случайным функционалом – поскольку в его состав входят вероятности p_k ; p_F и p_G .

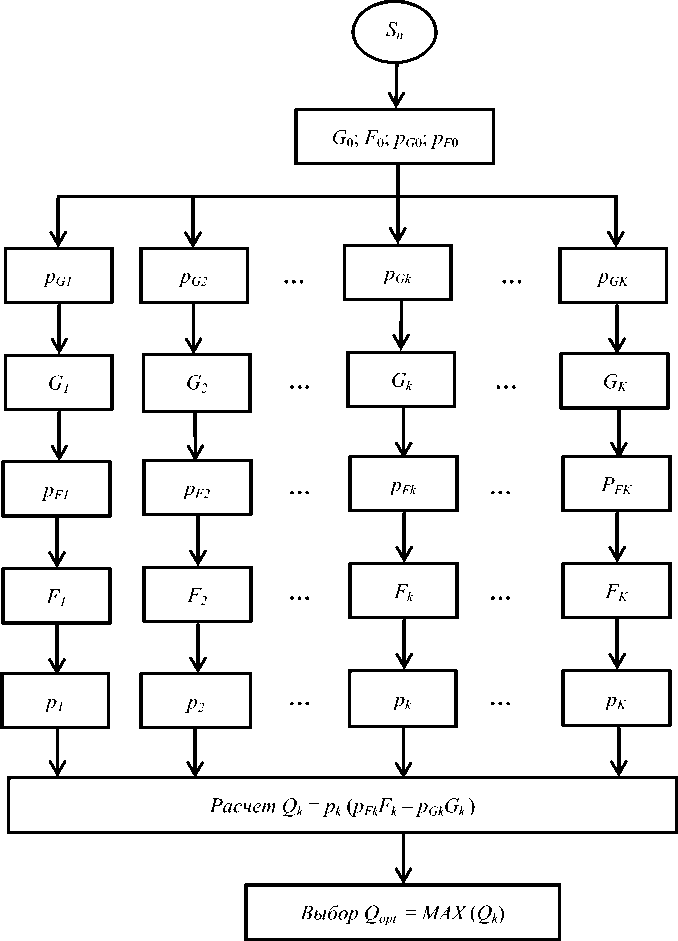
Рис. 1. К выбору оптимального сценария действий ЛПР S,, по критерию ФОП

Отметим, что предельно простой по составу («доходы» минус «расходы») ФОП (1) отличается достаточно сложной комплексной (объективной и субъективной, детерминированной и стохастической, статической и динамической и т.д.) структурой, где ключевым элементом является G_k – так как при отсутствии необходимых ресурсов о его реализации речи быть не может. При анализе ФОП необходимо рассмотреть и промоделировать следующие связи:

• -    G_k и p_G , на предмет того, есть ли возможность собрать нужные ресурсы, как уже было сказано, хотя бы для начала проекта;

• -    G_k и F_k , поскольку ЛПР надо знать, «стоит ли игра свеч»: для этого можно рассмотреть некий соответствующий исходным параметрам G ₀ и F ₀ начальный вариант («нулевой», базовый, бесприбыльный и т.п. сценарий), принимаемый за условную точку отсчета, относительно которой будет реализована дальнейшая стратегия

«синтеза через анализ» рассматриваемой СС при помощи СИМ по МДМ;

• -    G_k и p_F , так как, не собрав необходимые ресурсы и не имея под них гарантий, нельзя начинать проект: успех может быть неприемлемо маловероятным и получить выигрыш F_k от его реализации вряд ли удастся;

• -    G_k и p_k , в силу того, что получить разрешение «сверху» (в форме утверждения плана действий ЛПР в надсистеме) на реализацию проекта без необходимых ресурсов тоже вряд ли возможно;

• -    F_k и p_k , поскольку указанное разрешение «сверху» без весомого стимула в виде реальной возможности выигрыша F_k также обеспечить трудно;

• -    p_k и p_G ; p_F – если считать, что вероятность начала проекта обусловлена перспективой получения необходимых ресурсов и возможностью достижения цели в виде выигрыша F_k .

Схема выбора оптимального (наилучшего из рассматриваемых вариантов) сценария по критерию Q_opt = MAX(Q_k) показана на рис. 1. Вероятность одобрения k -го сценария в рамках предложенной в [4] экспоненциальной модели Q_k примем равной

Pk = 1 - exp (-p_G Pf G_k F_k/ G_o F_o), (5) так как чем больше значения «позитивных» рисков Pg G_k / Go получения ресурса и Pf F_k / Fq успешного достижения поставленной цели по сравнению с базовым сценарием, тем больше вероятность выбора и утверждения данного варианта реализации проекта.

Отметим, что как при Pg G_k/ G_o>> 1, так и при p_F F_k / F_o » 1, здесь имеет место p ≈ 1, тогда как при p_G G_k/G₀ « 1 или Pf F_k / F_o « 1, напротив, p_k ≈ 0, что также соответствует условиям моделирования СС. Данная часть процесса формирования ФОП отражает его объективную сторону, поскольку все вероятности здесь выступают в роли формальных коэффициентов (неизвестных ЛПР в настоящее время), а ресурсы и предполагаемые выигрыши могут быть определены детерминированными способами.

Субъективность ФОП проявляет себя при устранении неопределенностей путем конкретизации значений pG и pF , что на практике может быть сделано лишь с помощью эвристических (экспертных) методов группой привлеченных ЛПР. Поскольку, согласно схеме рис. 1, выбор вероятностей pG и pF предваряет оценку связанных с ними значений Gk и Fk , от «правильности» действий экспертов здесь непосредственным образом зависит исход СИМ. Отметим, что теоремы и леммы классической теории вероятностей в рамках концепции «риск как неопределенность» не всегда подходят к рассматриваемой ситуации, где более продуктивной является концепция «риск как возможность».

Анализ состава и структуры ФОП

Важной частью анализа ФОП является исследование связи между ресурсом G_k и ожидаемым выигрышем F_k – для решения данной задачи представим ресурс и выигрыш как

G_k = Go + ^G_k; F_k -F₀ + AF_k, (6)

после чего запишем (1) в следующем приближенном виде:

Qk -Pro \_Pfo (Fo + AFO -p_G0 (Go + ^G_k )], (7)

где принято, что Pk ~PkFPf ~ Pfo", Pg ~Pgo, что, строго говоря, справедливо при G_k » G_o. Перегруппировав слагаемые в правой части (4), получим

Qk = Qo + A Qk, где Qo ~ Pko (Pro Fq ~Pgo Gq) ~ О – наш условный «ноль», то есть выигрыш, соответствующий базовому сценарию, а также

^Qk = Fa-o ( Pfo ^Fk —poo ^Gk ), откуда при Pfo ~Pgo и^о -рюРсо следует

NQk- P,^GkaF;AGk-\)^

Po ^Gk(dFk/dGk — 1).(10)

Таким образом, в первом приближении связь между G_k и F_k определяется производной dF_k / dG_k : если dF_k /dG_k < 1, рассматриваемый k -ый вариант не имеет преимуществ перед базовым сценарием, в то же время наилучшим следует считать вариант, при котором dF_k/dG_k = MAX. Данный момент формализации ФОП представляется существенным, поскольку позволяет сформировать критерий при проведении СИМ по МДМ, «понятный» не только ЛПР, но и компьютеру.

Отметим, что условия Pk ~ Pro S Pf ~ Pfo", Pg ~ Pgo и Pfo ⁼ Pgo не представляются жесткими ограничениями, поскольку данные вероятностные коэффициенты все равно задаются, а впоследствии уточняются эвристическими экспертными методами, которые не могут давать точные (однозначные и надежно достоверные) результаты. Подставим (5) в (4) и сформируем ФОП в итоговом виде, пригодном для проведения СИМ по МДМ:

Qk = [l- exp к-p_Gp_F G_k F_k / G_o F_o)] x ^x (Pf F_k— pc G_k\

При дальнейшем анализе ФОП возникают два вопроса: во-первых, существует ли сценарий, при котором в (11) достигается оптимум Qopt ; во-вторых, каким в таком случае должен быть ресурс G_opt по сравнению с G ₀, который необходим для получения базового выигрыша F ₀. Ответ на эти вопросы был дан в [6], где показано, что

G_opt ~F_a/2, (12)

то есть, во-первых, искомый оптимум существует (в частном случае он может соответствовать и базовому сценарию), во-вторых, при наиболее целесообразном сценарии затраты на него должны составлять примерно половину прогнозируемого выигрыша. Подставив (12) в (11), получаем

Q_opt=V\-exp<-F₀!2 G^FJl. (13)

Таким образом, согласно (12)-(13), приступая к выполнению проекта, ЛПР S_n должен исходить из того, что выигрыш (в денежном выражении – выгода, прибыль) будет как минимум вдвое превышать расходы, связанные с реализацией наилучшего (но, возможно, и наиболее дорогостоящего) сценария.

Особенности разных подходовк анализу ФОП

Важное практическое значение имеет вопрос о том, в каких случаях наиболее целесообразен объективный подход к анализу ФОП, а в каких случаях – субъективный. Ясно, что на первый план здесь выходит специфика решаемой задачи и ее конкретные исходные условия, которые определяют, с каким «видом» неопределенности знаний и, соответственно, с какой вероятностью (объективной или субъективной), моделирующей эту неопределенность, ЛПР имеет дело в рассматриваемой ситуации.

Поясним сказанное на двух примерах из теории игр – максимально простых и универсальных. Выбирая «вслепую» карту из колоды и пытаясь установить, какая это карта по своим параметрам, мы «работаем» с объективной вероятностью – поскольку принадлежащая данной колоде игральная карта существует сама по себе, независимо от нашего сознания, и мы до определенного времени просто не знаем, какая она, но хотим оценить последствия этого незнания при разных вариантах развития событий. Переводя ситуацию в область оценки ФОП, можно, по аналогии, утверждать, что в природе уже имеется некий готовый вариант его реализации согласно (1), устраивающий нас в наибольшей мере, однако мы не знаем точно, какой это вариант, и хотели бы приблизиться к нему, используя объективный вероятностный подход.

Субъективная вероятность соответствует совету «лошадью ходи» в знаменитой кинокомедии, когда игрок сам определяет будущую ситуацию, и она непосредственным образом зависит от познавательной активности, опыта и профессиональной подготовки – то есть от объема и качества аксиологических знаний ЛПР, а также от стечения обстоятельств. Понятие неопределенности знаний в данном случае представляется существенно более богатым и разнообразным, но с большим трудом поддающимся управлению извне – поскольку не каждого ЛПР можно убедить или заставить действовать против его личной воли. Ограничимся здесь замечанием, что преодоление неопределенности знаний в процессе формирования ОМС на основе субъективного вероятностного подхода и соответствующее ему определение ФОП согласно (2) требуют от ЛПР значительных совместных усилий.

Заключение

Опыт показывает, что поведение и развитие СС в целом ряде случаев не подчиняется известным ЛПР закономерностям, идет по непредсказуемым для них сценариям и незапланированным путем [12]. В этой ситуации, с одной стороны, трудно воспользоваться критерием ФОП [10-11] непосредственно в виде (1)-(2), но, с другой стороны – так же трудно представить себе более подходящий по своим возможно стям и характеристикам способ поддержки действий ЛПР, чем СИМ по МДМ [1-4].

Это объясняется тем, что присущие сведениям об исследуемых СС неточности и неадекватности, возможные ошибки и неизбежные погрешности, а также любые другие неопределенности, воздействующие в качестве случайных факторов на результаты СИМ, можно не только учесть при помощи технологии ММК, но и определить степень их негативного влияния на качество принимаемых решений – с тем, чтобы скорректировать его до приемлемых пределов.