Функциональные связи морфометрических характеристик деревьев ели подпологовой популяции в березняках южной тайги

Автор: Дерюгин А.А., Глазунов Ю.Б.

Журнал: Лесохозяйственная информация @forestry-information

Статья в выпуске: 2, 2021 года.

Бесплатный доступ

В статье рассмотрена возможность установления в статике зависимостей между морфометрическими характеристиками популяции деревьев ели под пологом березняков южной тайги, находящихся в стадии возмужания и зрелости. Наличие и тесноту связи между показателями устанавливали методом парной корреляции, который позволяет выявить связь между двумя параметрами на фоне воздействия других. Уравнения связи принимали в случае, если коэффициент детерминации R2 ≥ 0,60. При меньшем значении модель не рассматривалась. Установленные зависимости подразделяются на три группы: связи характеристик ствола; связи морфометрических характеристик с возрастом; связи между параметрами крон и стволов. В статье приведены конкретные уравнения регрессии, которые могут применяться при проведении исследований в подпологовых популяциях ели; при этом целесообразно выбирать уравнения, характеризующиеся более высокими значениями коэффициента детерминации и меньшими значениями ошибок аппроксимации.

Еще

Ель под пологом березняков, морфометрические характеристики, возраст, парная корреляция, зависимости, уравнения регрессии, южная тайга

Короткий адрес: https://sciup.org/143175758

IDR: 143175758 | DOI: 10.24419/LHI.2304-3083.2021.2.02

Текст научной статьи Функциональные связи морфометрических характеристик деревьев ели подпологовой популяции в березняках южной тайги

Для установления связей между различными характеристиками деревьев в лесной таксации и лесоводственных исследованиях часто используют метод аппроксимаций, который позволяет по небольшой выборке выявить закономерности в виде статистических моделей и использовать их на практике в качестве основы количественных методов моделирования. Данный метод находит применение при построении графиков высот и классов роста, составлении таблиц хода роста древостоев различных древесных пород и моделей динамики роста древостоев, широко используется при установлении связей отдельных фракций фитомассы деревьев с их высотой и диаметром ствола [1–14]. В настоящее время функциональные связи между морфометрическими характеристиками деревьев в чистых древостоях хорошо изучены. В отношении же объекта исследований (популяция ели под пологом мелколиственных древостоев) изучению подобных связей не уделялось должного внимания.

Цель работы – установить функциональные связи между морфометрическими характеристиками деревьев ели европейской (Picea abies L.H. Karst.), произрастающих под пологом березовых древостоев, находящихся в возрастных стадиях возмужания и зрелости.

Объекты и методика исследований

В основу статистического анализа положены данные измерений параметров деревьев ели на 9 постоянных пробных площадях (ППП), заложенных сотрудниками Института лесоведения РАН в районе действия Северной ЛОС (Рыбинский район Ярославской обл.). Насаждения на ППП – березняки в конце возрастных стадий возмужания и зрелости [15]. В составе первого яруса присутствует осина. Во втором ярусе насаждения в стадии возмужания преобладает береза, в стадии зрелости – ель. Подрост представлен исключительно елью (табл. 1).

На заложенных в березняках ППП у 581 дерева ели (387 в стадии возмужания и 194 дерева в стадии зрелости) были измерены высота, диаметры стволов на высоте 0,1 и 1,3 м, протяженность крон и радиусы горизонтальной проекции крон, определены возраст, объемы крон и стволов. Для адекватной оценки связей в анализ были включены данные только по нормальным (здоровым)

Таблица 1. Средние характеристики насаждений на объектах исследований

Ярус Состав Число деревьев, тыс. шт./га Средние Сумма поперечного сечения стволов на высоте 1,3 м, м2/га Запас стволовой древесины, м3/га возраст, лет высота, м диаметр ствола на высоте 1,3 м, cм Березняки в конце стадии возмужания – возраст 41–50 лет 1 84Б 0,93 48 22,1 17,3 20,50 209 16Ос 0,21 48 22,1 17,1 4,21 40 2 62Б 0,62 34 11,2 7,0 2,33 13 38Е 0,55 42 6,3 6,6 1,85 8 Подрост 100Е 3,56 24 1,9 - - - Березняки в конце стадии зрелости – возраст 71–80 лет 1 89Б 0,55 75 27,3 24,7 25,41 307 11Ос 0,04 77 29,0 32,3 2,87 37 2 84Е 1,31 67 10,8 10,5 11,31 69 16Б 0,16 59 17,6 12,2 1,70 13 Подрост 100Е 0,71 52 4,1 - - - деревьям, не имеющим видимых повреждений [16]. Наличие и тесноту связи между показателями устанавливали в статике методом парной корреляции, который позволяет выявить связь между двумя параметрами на фоне действия других. По значению коэффициентов корреляции (r) определяли целесообразность проведения регрессионного анализа для получения соответствующих уравнений при тесноте связи не меньше умеренной (r > 0,50). Уравнения связи принимали в случае, если коэффициент детерминации R2 ≥ 0,60. При меньшем значении модель не рассматривалась.

Для обработки данных был использован пакет статистического анализа Excel, а также программа Table Curve 2Dv 5.01.01.

Результаты и обсуждение

На начальном этапе поиска адекватных моделей связи был проведен корреляционный анализ в отношении рассматриваемых характеристик деревьев подпологовой ели для березняков в возрастных стадиях возмужания и зрелости раздельно. Установлено, что под пологом березняков в стадии возмужания почти все рассматриваемые показатели деревьев ели характеризуются высокой и очень высокой теснотой связи. Коэффициенты парной корреляции изменяются от 0,67 до 0,98 (табл. 2).

В березняке в стадии зрелости высокая теснота связи для деревьев ели сохраняется по большинству показателей (r = 0,72–0,97). Исключение составляют связи отдельных показателей с возрастом. Если в березняке в стадии возмужания r = 0,67–0,85, то в стадии зрелости r = 0,18–0,31, т. е. связь очень слабая или почти отсутствует. Данное обстоятельство объясняется тем, что при переходе березняков от стадии возмужания к стадии зрелости возрастная структура подпологовой ели несколько упрощается, существенно снижается коэффициент вариации возраста (с 30 до 9%). По-видимому, это уменьшает тесноту связи, что делает нецелесообразным поиск уравнений регрессии, отображающих зависимости рассматриваемых показателей от возраста ели в березняках 70–80-летнего возраста, т. е. находящихся в конце стадии зрелости.

На следующем этапе был проведен поиск уравнений регрессии, отображающих связь между характеристиками деревьев. Эта процедура выполнена для деревьев ели, произрастающих в березняках рассматриваемых возрастных стадий и в целом для всего массива данных (581 дерево). В ходе сопоставления 82 полученных уравнений регрессии и оценки адекватности связей установлено, что уравнения связи можно разбить на 3 группы.

Первая группа – уравнения, характеризующие связь между характеристиками стволов

Таблица 2. Матрица коэффициентов парной корреляции между морфометрическими характеристиками деревьев ели, произрастающих под пологом березняков (светлый шрифт – березняки в стадии возмужания, полужирный шрифт – березняки в стадии зрелости)

Показатель	^D1,3	^D0,1	H	A	R K	L K	V K	V
^D1,3	1,00	1,00	0,96	0,31	0,76	0,83	0,80	0,97
^D0,1	0,98	1,00	0,96	0,29	0,75	0,83	0,81	0,97
H	0,94	0,96	1,00	0,28	0,74	0,87	0,80	0,94
A	0,79	0,87	0,85	1,00	0,20	0,21	0,18	0,27
R K	0,86	0,93	0,89	0,85	1,00	0,66	0,84	0,72
L K	0,90	0,94	0,98	0,78	0,86	1,00	0,88	0,85
V K	0,82	0,84	0,87	0,67	0,84	0,90	1,00	0,87
V	0,88	0,87	0,90	0,68	0,74	0,91	0,91	1,00

Примечание. D_1,3, D_0,1 – диаметр ствола соответственно на высоте 1,3 и 0,1 м; H – высота деревьев; A – возраст; R_K – средний радиус кроны; L_K – протяженность кроны; V_K – объем кроны; V – объем ствола.

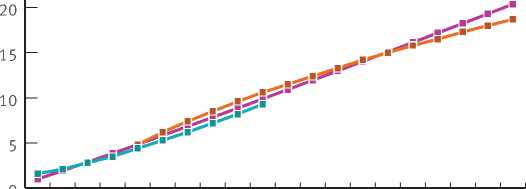
деревьев и уравнения связи между радиусом и объемом крон – VK = f(RK). В этой группе уравнения регрессии могут с достаточной достоверностью описывать связь для всего массива данных, что можно проиллюстрировать на примере связи – H = f(D1,3) (рис. 1). Уравнения регрессии приведены в табл. 3.

H, м

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

D1,3, см

Стадия зрелости Стадия возмужания

Общая

Рис. 1. Связь высоты деревьев ели с диаметром ствола на высоте 1,3 м

находящихся в стадии возмужания. Это относится к связям рассматриваемых характеристик с возрастом. В табл. 4 приведены уравнения, где возраст выступает в качестве аргумента (например, H = f (A)) и в качестве зависимой величины (например, A = f (H)).

Рассматриваемые зависимости могут быть аппроксимированы степенной и линейной функциями. Теснота связей значений возраста существенно меньше, чем теснота связей показателей, характеризующих ствол деревьев. Использовать две последние зависимости (VK = F(A), V = F(A)) нецелесообразно, так как R2 < 0,60. Уравнения связи достоверны при уровне значимости а = 0,01 (фактические значения F-критерия изменяются от 246 до 7 564, что выше табличного значения 3,80).

К третьей группе относятся зависимости, характеризующие кроны деревьев. Развитие крон во многом зависит от напряженности отношений в ярусах древостоя. В березняках в возрастной стадии возмужания популяция ели

Таблица 3. Уравнения регрессии, характеризующие связи для всего массива данных

№ п/п	Функция	Ед. изм.	Диапазон значений аргумента	Уравнение регрессии	R²	F-критерий фактический	Ошибка уравнения регрессии
1	H = f (D_0,1)	м	0,5–27,0 см	H = -0,069 + 0,497 X D₀ , ₁ ^1,241	0,96	13 248	0,7
2	H = f (D_1,3)	м	0,4–26,0 см	H = 0,315 + 0,861 x D_1>3 ^1,054	0,96	6 135	0,8
3	D 0,1 = f (D 1,3 )	см	0,4–26,0 см	D₀₁ = 1,436 + 0,951 x D₁₃	0,99	63 334	0,3
4	V = f (D_0,1)	дм ³	0,5–27,0 см	V = 0,0926 x D₀₁ ² - ⁵²¹	0,92	32 818	4,4
5	V = f (D 1,3 )	дм ³	0,4–26,0 см	V = 0,194 x D_{1 3} ² - ²⁹⁷	0,99	44 178	3,7
6	V = f (H)	дм ³	0,5–24,0 м	V = 0,098 x H ² - ⁵⁵¹	0,98	35 403	4,3
7	V K = f (R K )	м ³	0,1–2,4 м	V K = 0,002+3,117 x R K ^3,319	0,86	1 845	2,8

Большинство связей может быть аппроксимировано степенными уравнениями с коэффициентами детерминации R2 = 0,86–0,99. Фактические значения F-критерия существенно выше табличного (3,80) при уровне значимости а = 0,01, что свидетельствует о высокой достоверности полученных уравнений.

Ко второй группе можно отнести уравнения, характеризующие связи только для березняков, представлена главным образом подростом со средней сомкнутостью крон 0,62. В березняках в стадии зрелости значение этого показателя возрастает до 0,80. Кроме того, в таких березняках ель выходит во второй ярус древостоя, её кроны начинают контактировать с кронами березы. Это сказывается на развитии крон ели и, соответственно, снижает тесноту связи между характеристиками деревьев. В третьей группе

Таблица 4. Уравнения связи возраста с характеристиками деревьев ели в березняках в конце стадии возмужания (возраст 41–50 лет)

№ п/п Функция Ед. изм. Диапазон значений аргумента Уравнение регрессии R2 F-критерий фактический Ошибка уравнения регрессии 1 A = f(D0,1) лет 0,4–15,0 см A = 16,416 х D010’431 0,79 1 463 4 2 A = f(D1,3) лет 0,4–9,5 см A = 19,898 + 4,759 х D130•752 0,62 246 4 3 A = f(H) лет 0,3–9,0 м A = -77,218 + 97,63 х H0-10 0,78 7 564 4 4 H = f(A) м 7–48 лет H = 0,023 + 0,003 х A2 0,73 1 045 1 5 D0,1 = f(A) см 7–48 лет D0,1 = -0,417 + 0,029 х A 0,76 1 198 1,2 6 D1,3 = f(A) см 7–48 лет D13 = -3,840 + 0,240 х A 0,62 485 1,2 7 RK = F(A) м 7–48 лет RK = -0,194 + 0,034 х A 0,72 1 000 0,2 8 LK = F(A) м 7–48 лет LK = 0,002 х A1'991 0,62 636 1 9 VK = F(A) м3 7–48 лет VK = -514 + 0,00010 х A3 0,50 383 2,4 10 V=F(A) дм3 7–48 лет V = 0,00000005 х A5"135 0,55 479 3,4 связи были рассмотрены отдельно для березняков этих возрастных стадий. Целесообразность такого подхода можно проиллюстрировать на примере двух функций – VK = f(D1,3) и VK = f(H) (рис. 2). Установленные зависимости приведены в табл. 5.

изменяется от тесной до весьма тесной. Фактические значения F-критерия (485–9 311) существенно больше табличного (3,80) при уровне значимости а = 0,01.

Для березняков в стадии зрелости не удалось установить достоверные связи по 4 функциям

2 4 6 8 10 12 14 16 18 20 22 24 26

D1,3, см

Стадия возмужания Стадия зрелости

Рис. 2. Связи объема крон деревьев ели с диаметром стволов (А) и высотой (Б)

Рассмотренные зависимости могут быть аппроксимированы преимущественно степенной функцией, реже линейной. Для березняков в стадии возмужания все уравнения отвечают принятым требованиям (R2 ≥ 0,60). Коэффициенты детерминации по зависимостям находятся в диапазоне от 0,74 до 0,96, т. е. характер связи

(см. табл. 5, уравнения № 11–13, 15). Здесь значения коэффициента детерминации меньше принятого ограничения (R2 ≥ 0,60). Другие установленные зависимости характеризуются тесной связью (R2 = 0,73–0,80). Фактические значения F-критерия (372–743) существенно выше табличного (3,80) при уровне значимости а = 0,01.

Таблица 5. Уравнения связи показателей крон деревьев ели, произрастающих под пологом березняков

№ п/п	Функция	Ед. изм.	Диапазон значений аргумента	Уравнение регрессии	R²	F-критерий фактический	Ошибка уравнения регрессии
Ель под пологом березняков в стадии возмужания
1	R_K = F(D0,1)	м	0,4–15,0 см	R K = -0,247 + 0,51 x D₀₁ ⁰ , ⁵²⁴	0,88	1 394	0,1
2	R_K = F(D_1,3)	м	0,4–9,5 см	R K = 0,480 + 0,117 x D 1,3	0,74	830	0,1
3	R_K = F(H)	м	0,3–9,0 м	R K = -1,176 + 1,604 x H ⁰ , ²²⁸	0,85	1 074	0,1
4	L_K = F(H)	м	0,3–9,0 м	L K = 0,639 x H ¹ , ¹⁰⁸	0,96	9 311	0,3
5	L K = F(R K )	м	0,1–2,0 м	L K = 2,914 x R k ¹ ' ⁴²⁶	0,75	1 154	0,8
6	V_K = F(D_0,1)	м ²	0,4–15,0 см	V K = 0,036 x D₀₁ ² • ⁵⁸¹	0,82	1 731	1,4
7	V K = F(D 1,3 )	м ³	0,4–9,5см	V K = 0,240 + 0,092 x D ..²-'	0,77	485	1,7
8	V_K = F(H)	м ³	0,3–9,0 м	V K = 0,221 x H ¹ " ⁹⁵⁷	0,82	1 720	1,4
9	V_K = F(RK)	м ³	0,1–2,0 м	V K = 3,145 x R K ^3,167	0,88	2 961	1,2
10	V K = F(V)	м ³	0,01–29,3 дм ³	V K = 1,622 x V ⁰ ’ ⁹²⁷	0,84	1 965	2,1
Ель под пологом березняков в стадии зрелости
11	R_K = F(D_0,1)	м	5,5–26,9 см	R K = -0,557 + 0,564 x D^ ⁵	0,52	208	0,2
12	R K = F(D 1,3 )	м	4,8–26,1 см	R K = 0,322 x D 1 30.6 ⁰⁹	0,52	210	0,2
13	R_K = F(H)	м	4,1–23,8 м	R K = 0,512 + 0,076 x H	0,48	177	0,2
14	L_K = F(H)	м	4,1–23,8 м	L K = 2,158 + 0,009 x H ² , ³	0,80	372	0,9
15	L K = F(R K )	м	0,01–2,4 м	L K = 2,201 + 1,314 x R K ²	0,42	143	1,4
16	V K = F(D 0,1 )	м ³	5,5–26,9 см	V K = -0,646 + 0,022 x D₀₁ ² , ⁵	0,73	513	5,3
17	V K = F(D 1,3 )	м ³	4,8–26,1 см	V K = 0,825 + 0,022 x D .. ² '	0,73	512	5,0
18	V_K = F(H)	м ³	4,1–23,8 м	V K = 1,048 + 0,006 x H ³	0,77	639	4,8
19	V K = F(R K )	м ³	0,01–2,43 м	V K = 3,176 x R K ³ , ²⁹⁹	0,79	743	4,6
20	V K = F(V)	м ³	3,91–321,1 дм ³	V K = -0,513+0,216 x V	0,74	541	5,2

Выводы

К установлению связей между морфометрическими характеристиками деревьев ели подпологовой популяции необходимо подходить дифференцированно, учитывая фитоценотиче-скую обстановку под пологом березняков, находящихся в стадиях возмужания и зрелости.

Зависимости между параметрами стволов можно рассматривать без учета возрастных стадий формирования березняков.

Связь морфометрических характеристик стволов и крон деревьев ели с возрастом в статике может рассматриваться только для березняков в стадии возмужания. В березняках в стадии зрелости вариация возраста уменьшается, а теснота связи с характеристиками деревьев снижается до очень слабой.

Зависимости между параметрами крон, а также параметров крон деревьев с характеристиками стволов подпологовой ели следует рассматривать раздельно для березняков в стадиях возмужания и зрелости.

Выявленные зависимости аппроксимируются главным образом степенной функцией, реже линейной. Уравнения регрессии можно применять при проведении исследований в подпологовых популяциях ели, при этом целесообразно выбирать уравнения, характеризующиеся более высокими значениями коэффициента детерминации и меньшими значениями ошибок аппроксимации.

Список литературы Функциональные связи морфометрических характеристик деревьев ели подпологовой популяции в березняках южной тайги

Уткин, А.И. Биологическая продуктивность лесов. Методы изучения и результаты / А.И. Уткин // Итоги науки и техники. Сер.: Лесоведение и лесоводство. - М. : ВИНИТИ, 1975. - Т. 1. - С. 9-189.
Карманова, И.В. Математические методы изучения роста и продуктивности растений / И.В. Карманова. - М. : Наука, 1976. - 223 с.
Усольцев, В.А. Применение регрессионного анализа при исследовании возрастной динамики фитомассы березы и осины / В.А. Усольцев // Лесоведение. - 1976. - № 1. - С. 35-39.
Богачев, А.В. Методы таксации лесного и лесосечного фонда / А.В. Богачев, Н.С. Свалов // Итоги науки и техники. Сер.: Лесоведение и лесоводство. - М. : ВИНИТИ, 1978. - Т. 2. - С. 7-209.
Уткин, А.И. Методика исследований первичной биологической продуктивности лесов / А.И. Уткин // Биологическая продуктивность лесов Поволжья. - М. : Наука, 1982. - С. 59-71.
Опыт оценки массы крон мелколиственных древостоев по параметрам ветвей и ствола / Т.А. Гульбе, С.Г. Рождественский, А.И. Уткин [и др.] // Лесоведение. - 1991. - № 2. - С. 48-58.
Демаков, Ю.П. Диагностика устойчивости лесных экосистем / Ю.П. Демаков. - Йошкар-Ола : Марийский государственный технический университет, 2000. - 414 с.
Лебков, В.Ф. Аппроксимация образующей ствола и идентификация его формы функцией распределения / Н.Ф. Лебков // Лесной журнал. - 2002. - № 5. - С. 15-22.
Кузьмичев, В.В. Закономерности динамики древостоев / В.В. Кузьмичев. - Новосибирск : Наука, 2013. - 208 с.
Воробьева, И.А. Закономерности связи диаметров нижней части стволов деревьев в смешанных сосно-во-березовых древостоях юга Средней Сибири / А.И. Воробьева, А.А. Вайс // Хвойные бореальной зоны. - 2014. - Т. 32. - № 1-2. - С. 13-17.
Использование аллометрических зависимостей для оценки фитомассы различных фракций деревьев и моделирования их динамики / Ю.П. Демаков, А.С. Пуряев, В.Л. Черных [и др.] // Вестник государственного технического ун-та. Сер.: Лес. Экология. Природопользование. - 2015. - № 2 (26). - С. 19-36.
Вайс, А.А. Методические подходы к изучению соотношения диаметров деревьев на высоте 1,3 метра и на высоте пня / А.А. Вайс, И.А. Воробьева // Лесная таксация и лесоустройство. - 2015. - № 1 (52). - С. 16-19.
Белов, А.А. Регрессионное моделирование динамики радиального прироста сосны обыкновенной в загрязненных радионуклидами насаждениях Брянской области / А.А. Белов // Лесоведение. - 2017. - № 1. - С. 17-23.
Вайс, А.А. Аллометрические закономерности биологической продуктивности еловых насаждений / А.А. Вайс, Е.С. Кербис // Хвойные бореальной зоны. - 2019. - Т. 37. - № 3-4. - С. 214-222.
Рубцов, М.В. Возрастная динамика морфоструктуры и рост популяции ели под пологом березняков южной тайги / М.В. Рубцов, А.А. Дерюгин // Идеи биогеоценологии в лесоведении и лесоразведения. - М. : Наука, 2006. - С. 63-81.
Рубцов, М.В. Динамика состояния популяции ели под пологом березняков южной тайги Русской равнины / М.В. Рубцов, А.А. Дерюгин // Лесной журнал. - 2016. - № 2. - С. 47-58.

Еще

Статья научная