Функциональный синтез управления в однофазных электроприводах малой мощности

Методы теории автоматического управления, основанные на оперировании передаточными функциями, импульсными переходными характеристиками и т. п., имеют преимущества перед методами численного решения в части возможности проводить более глубокий анализ, делать меньшее число шагов при проектировании. Дальнейшее развитие теории автоматического управления дало возможность приспособить эти методы к цифровым вычислительным машинам. Одним из таких методов является спектральный метод, в котором при расчете используются алгебраические алгоритмы, позволяющие некоторые операции проводить в аналитической форме, что существенно сокращает машинное время. Он не имеет ограничений на порядок дифференциального уравнения, на число и характер переменных параметров, а также на число контуров с обратной связью [1].

Постановка задачи

В настоящее время для управления однофазным коллекторным двигателем последовательного возбуждения (ОДПВ) используются современные вентильные устройства, которые ставятся в цепь переменного или выпрямленного питающего напряжения [2–5]. При питании однофазного коллекторного двигателя от вентильного преобразователя работа ОДПВ имеет ряд специфических особенностей, обусловленных пульсациями питающего напряжения [6]. Появление дополнительных потерь в меди обмоток, стали магнитопровода и конструктивных элементах обусловлено наличием переменных составляющих в токе якоря и магнит- ных потоках машины. Увеличение потерь в меди связано как с возрастанием действующего значения тока якоря, так и со значительным повышением активных сопротивлений обмоток переменным составляющим тока. В общем случае гармонический состав тока якоря зависит от спектра гармоник выходного напряжения вентильного преобразователя и эквивалентного сопротивления якорной цепи для отдельных составляющих гармоник [7]. Эти и другие обстоятельства актуализируют задачу необходимости исследования электромагнитных процессов в цепях ОДПВ [8] и выявления основных функциональных зависимостей выходных характеристик от управляемых параметров.

Математическое описаниеи структурные схемы

Математическое описание вентильного электропривода с ОДПВ может быть представлено следующей системой дифференциальных уравнений [6, 9, 10]:

и ( t ) = R d i ( t ) + d^ + kv M ( t M t );

dt

M (t) - Mc (t ,Q) = Jd^t-;       > dt

^{M (} t ) = v m ⁽ t ) i ⁽ t );

U(t) = F(9, to, m, vm , V, t), где U(t) – напряжение питания двигателя; i(t) – ток якоря; Rd – активное сопротивление цепи якоря; Ω(t) – частота вращения вала; k – коэффициент пропорциональности ЭДС вращения; ψ(t), ψM (t) – полное потокосцепление и потокосцепление взаимной индукции; M(t), Mc(t) – электромагнитный момент и момент статического сопротивления на валу; J – момент инерции двигателя; F(θ, ω, m, ψM, ψ, t) - обобщенная функция, моделирующая выходное напряжение преобразователя; θ - угол регулирования; ω - угловая частота сети; m – число фаз преобразователя; t - время.

Для составления алгоритма работы ОДПВ как объекта управления при детерминированных входных воздействиях и начальных условиях необходимо получить выражения для двухмерных нестационарных передаточных функций и нестационарных спектральных характеристик выходных переменных: скорости вращения двигателя Ω( t ), момента M ( t ) и тока цепи якоря I ( t ). Учитывая, что выходные координаты двигателя описываются кусочно-гладкими, монотонными функциями, целесообразно в качестве базисной принять систему нестационарных ортонормированных тригонометрических функций, что значительно упрощает выражения для спектральных характеристик. Учитывая свойства линейности нестационарных спектральных характеристик, производной функции времени при ненулевых начальных условиях и произведения функций времени, получим (здесь и далее нижний индекс «с» будет указывать на спектральную характеристику соответствующей функции):

E c ( t ) - P ( t , t )v c ( t ) - R d I_c ( t ) = U c ( t ) + V q A c ( t );

J ^-1 P_c1 ( t , t )Q_c ( t ) - M c ( t ) = J -1Q_OA_C ( t ) - M c ( t )A( t );

cc        c          c              0 c         c c

E c ( t ) = kv M ( t )Q c ( t );

M c ( t ) = v M ( t ) I c ( t );

Uc (t) = Acc (t, t) UQ( t), где Pcc(t, t) - двумерная нестационарная передаточная функция дифференцирующего звена; Acc(t, t) - двумерная нестационарная передаточная функция вентильного преобразователя, представленного звеном с переменным коэффициентом усиления; Vccc(t, t) - трехмерная передаточная функция множительного звена; Ωc(t), Ic(t), Uc(t), Ec(t), ψc(t), ψcM(t), Mc(t), Mcc(t) - нестационарные спектральные характеристики частоты вращения, тока, выходного напряжения вентильного преобразователя, ЭДС вращения, полного потокосцепления, потокосцепления взаимной индукции обмоток якоря и возбуждения, электромагнитного момента и момента сопротивления на валу двигателя, соответственно; Ω0, ψ0 - начальные условия; Δс(t) -нестационарная спектральная характеристика дельта-функции; Uc0(t) - нестационарная спектральная характеристика модулирующей функции входного напряжения; J - момент инерции системы электропривода, приведенный к валу электродвигателя.

Для составления многомерной передаточной функции исследуемой системы вентильного электропривода с ОДПВ были упорядочены внешние воздействия и выходные сигналы в виде матриц-столбцов g (τ) и x (τ):

g ⁽ t )= [ U (0 M^c (t) t q⁽ t) Q q V o ] ;

X (t )= [Q(t) M (t) I (t) ]т, где М с(τ) – статический момент на валу двигателя; t0 – начальное значение времени на рассматривае- мом интервале.

Матрица двумерной нестационарной передаточной функции системы вентильного электропривода с ОДПВ имеет вид:

Ф( t , t )=

Ф 11 ( t , t )   Ф_п( t , t )    -   Ф 1v ( t , t )

Ф ц1 ( t , t )  Ф_Ц 2 ( t , t )   -   Ф_ц v ( t , t )

где Ф µν ( t , t ) – передаточные функции, характеризующие связь μ-го выхода (μ = 1, 2, 3) с ν-м входом (ν = 1, 2, 3, 4, 5).

Приведенные зависимости позволили построить структурную схему ОДПВ с питанием от вентильного преобразователя, представленную на рис. 1. Здесь операторные изображения заменены спектральными характеристиками сигналов.

Нелинейность, связанная с зависимостью абсолютной магнитной проницаемости от тока, ап- проксимирована усеченным ортонормированным рядом [11, 12].

С учетом симметричности нелинейности магнитную проницаемость можно выразить:

ц j = a 1 1 + a 3 1 ³ + a 5 1 ⁵, 0 <  I <  I max .

Алгоритм расчета (элементов) матрицы удобно проводить таким образом, чтобы передаточные функции определять на фиксированном временном интервале, а дальнейший процесс расчета продолжить методом припасовывания.

На рис. 2 приведена структура расчета нелинейной системы вентильного электропривода с ОДПВ для нахождения матрицы Ф 31 ( t , t ). Эта структура представлена в виде параллельного соединения цепей с передаточными функциями Ф 1 ( h , i 1 , t ), Ф 2 ( h , i 1 , i 2 , t ), Ф 3 (h, i 1 , i 2 , i 3 , t ), Ф 4 ( h , i 1 , i 2 , i 3 , i 4 , t ), Ф 5 ( h , i 1 , i 2 , i 3 , i 4 , i 5 , t ), Ф 6 ( h , i 1 , i 2 , i 3 , i 4 , i 5 , i 6 , t ). Коэффициенты С 1 , С 2 и С 3 взяты из многомерной нестационарной передаточной функции нелинейного звена μ( I ). Таким образом, матрица Ф₃₁( t , t ) определяет зависимость тока I (τ), которая получена суммированием всех реакций системы вентильного электропривода с ОДПВ.

Полученные соотношения приводят к уравнениям, позволяющим исследовать переходные и квазиустановившиеся процессы в ОДПВ при питании от вентильного преобразователя:

I ( t ) = Ф 31 ( t , t )U ( t ) + Ф 32 ( t , t ) M^c ( t ) +

+ О о Ф з4 ( t , t )A( t ) + V o Ф з5 ( t , t )A( t );

M ( t ) = Ф 21 ( t , t )U ( t ) + Ф 22 ( t , t ) M^c ( t ) + + О о Ф 24 ( t , t )A( t ) + V o Ф 25 ( t , t )A( t );

Q( t ) = Ф 11 ( t , t )U ( t ) + Ф 12 ( t , t ) M^c ( t ) + + О)Ф_М ( t , t )A( t ) + V o Ф 15 ( t , t )A( t ).

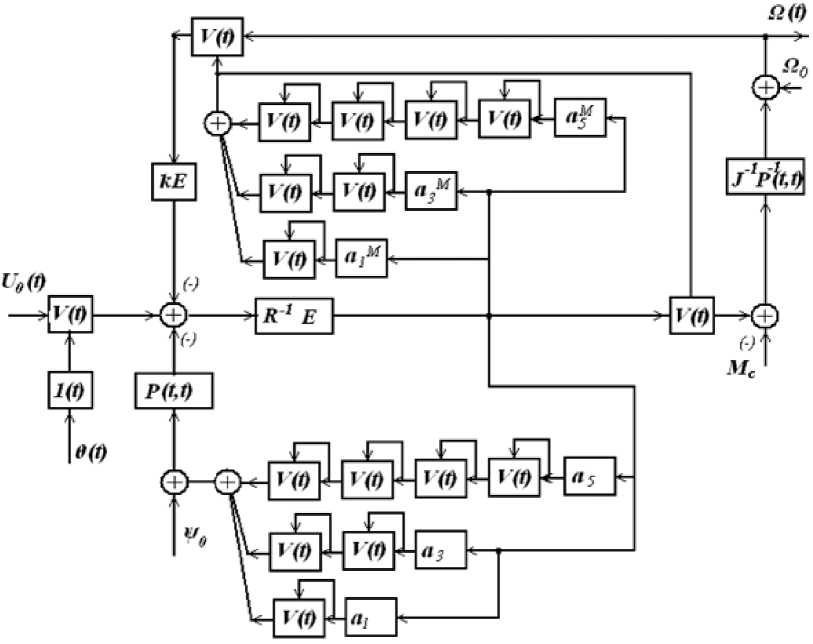
Рис. 1. Структурная схема ОДПВ с питанием от вентильного преобразователя

Электромагнитные процессы при синусоидальной форме питающего напряжения ОДПВ хорошо изучены, поэтому в настоящее время большой интерес представляет исследование электромагнитных процессов при питании ОДПВ от вентильного преобразователя с целью выявления особенностей и новых закономерностей.

Выходное напряжение вентильного преобразователя можно определить следующим образом [2]: и (т,6) =

ОТ

= U m E sin l ^T - n = 0    V

2π n m

, (  2n n Л (   2nn

1 I т---6 1- 1 1 т--

V    m   J V    m

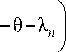
где U m – амплитуда питающего напряжения; n – номер вентиля, отсчитываемого от момента подачи первого сигнала управления; θ – угол управления n -го включенного вентиля; τ – текущая угловая координата питающего напряжения; λ _n – угол проводимости включенного вентиля; 1( F ) – единичная функция, которая равна 1, при F > 0 и равна 0 при F ≤ 0.

Обобщенная функция U (τ, θ) может быть представлена в спектральном виде множительным звеном, на один вход которого поступает непрерыв-

L 2nn)       „ - „ ный сигнал Um sin I т--I, а на другой - после-V m J

ОТ довательность импульсов Е 1(т - 6). Слагаемое Лn n=0

учитывает, что нестационарная спектральная характеристика выходного напряжения преобра- зователя за пределами нестационарного отрезка tn

2π n

= т---6 - л n равна нулю.

m

Спектральные характеристики входных сиг- налов множительного звена определены по следующим выражениям:

B c ( t ) = S c [ U m ^{sinro t} ] =

U m ( roft ) ( cosro t - 1 ) , при i = 0;

U m roj2t ( i ²n² - ro² t ² ) [ ( - ! ) i cosro t - 1 ] , при i = 1,2,

A c ( t ) = S c [ 1 ( ro t - 6 ) ] =

( t - ⁶) 4.

при i = 0;

V2 7 ( i n ) ¹ sin ( t - 6 ) , при i = 1,2,....

Тогда нестационарная спектральная характеристика выходного напряжения вентильного преобразователя будет иметь вид

Uc (t) = ЕЕ Vccc (h, i, k, t) Ac (k, t)Bc (i, t )• ik

Передаточную функцию вентильного преобразователя как звена системы автоматического регулирования можно представить в виде

W_c ^np( t ) = E V ccc ( h , i , k , t ) A c ( k , t ).

k

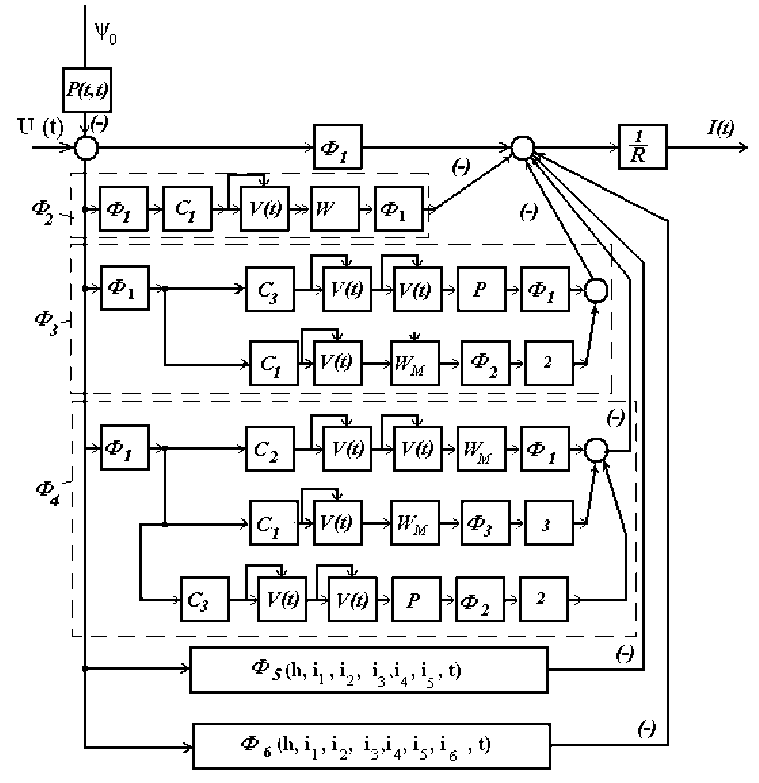
Рис. 2. Структура расчета нелинейной системы

На рис. 3 приведен алгоритм расчета системы вентильного электропривода с ОДПВ. Расчет проводился с использованием метода припасовыва-ния. Вначале определялись начальные условия в системе вентильного электропривода с ОДПВ, далее на основе принятой системы базисных орто-нормированных функций находились их спектральные характеристики. Аналогично определялись спектральные характеристики других входных сигналов и передаточные функции всех звеньев системы вентильного электропривода с ОДПВ. Расчет и исследование системы вентильного электропривода с ОДПВ производился на выбранном интервале времени t j , при этом конечные значения выходных координат движения принимались начальными для последующего t j ₊₁-го интервала времени. Расчет выполнен по одним и тем же уравнениям, менялись лишь начальные условия на каждом интервале.

Разработанный алгоритм расчета реализован в среде MatLab, что позволило исследовать работу вентильного преобразователя с ОДПВ.

На рис. 4, 5 представлены результаты исследований.

Анализ зависимостей, представленных на рис. 4 показал, что время проводимости тока вентилем преобразователя зависит от угла управления θ и скорости вращения Ω. Причем при увеличении скорости вращения ОДПВ время проводящего состояния тока вентилем уменьшается.

На рис. 5 приведены зависимости угла проводимости ω t вентилей преобразователя электропривода с ОДПВ от соотношения тока якоря к скорости вращения двигателя при разных углах управления. Как видно из приведенных графиков, представленные зависимости имеют линейный характер, что повышает их практическую значимость [13].

Полученные зависимости угла проводимости вентилей преобразователя при различных значениях скорости вращения двигателя Ω и его нагрузки на валу можно использовать в приближенных расчетах вентильных систем электропривода с ОДПВ.

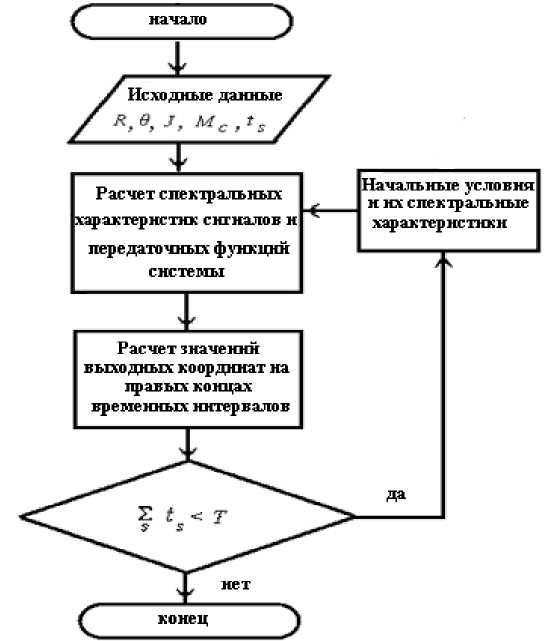
Рис. 3. Алгоритм численного расчета электромагнитных процессов вентильного электропривода с ОДПВ

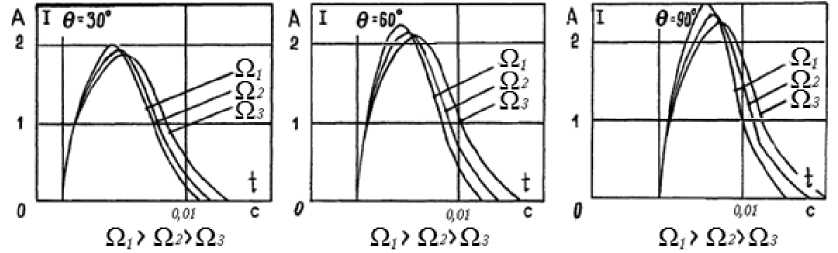
б)

а)

в)

Рис. 4. Зависимости времени проводимости тока вентилем преобразователя от угла управления θ , и скорости вращения Ω

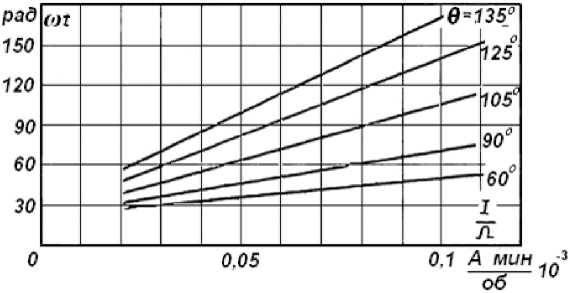
Рис. 5. Зависимости угла проводимости вентилей преобразователя от соотношения тока якоря к скорости вращения двигателя при разных углах управления

Заключение

В результате проведенных исследований установлено, что:

– моделирование объектов регулирования, отличающихся наличием существенных нелинейностей типа «кривая намагничивания», «множительное звено», а также устройств с зависимыми от времени параметрами целесообразно проводить, используя спектральный метод расчета нелинейных нестационарных систем;

– предложенная методика аналитического определения параметров движения на примере ОДПВ, питаемого от вентильного преобразователя показывает, что расчет основных величин (тока, напряжения, частоты вращения) целесообразно проводить только для мгновенных значений.

Работа выполнена в рамках программы ВИУ ТПУ 2017-2018.