Функционирование информационных радиоэлектронных средств в различных точках факторного пространства геомагнитных аномалий

Введение . Разработка современных радиотехнических и радиофизических систем различного уровня сложности требует всестороннего учета влияния случайных процессов, которые протекают в их информационных сечениях. Автоматизация обработки пространственно-временных сигналов в таких системах приводит к необходимой формализации и алгоритмизации процедур выявления аномальных результатов измерений, которые представляют либо полезную информацию, либо должны исключаться при дальнейшей обработке. Это приводит к некоторым особенностям описания, выбору адекватных моделей протекающих физических процессов и случайных воздействий. В данной работе предпринята попытка рассмотрения специфических особенностей влияния локальных геомагнитных аномалий на реакцию дипольных и рамочных антенных радиоэлектронных информационно-измерительных систем.

Постановка задачи . Динамика пространственно-временных локальных геомагнитных аномалий может быть вызвана процессами, связанными с относительными перемещениями намагниченных тел и приемных антенн.

Пренебрегая малостью геомагнитных аномалий неземного происхождения напряженность локального геомагнитного поля (ЛГП) можно представить в прямоугольной системе координат суммой напряженностей магнитного поля Земли (МПЗ) H 3 ( x , y , z ) и локальной намагниченной области H t ( x , y , z ) :

Поле

M ( x , y , z )

H a ( x , У , z ) = H з ( x , У , z ) + H r ( x , у , z )            (1)

Ht (x, y,z) , обусловленное намагниченностью некоторой области пространства может быть определено по известным [1, 2] соотношениям через век- торный потенциал:

A ( R ) -

ц 0 M x R

4 R ³

где μ ₀ =4π·10^-7 Гн⁄м – магнитная постоянная,

M J = M x i + M y J + M z k ,    JR = ( x - X r ) J + ( У - У т ) 7 + ( z - Z r ) k ,

R -I / г| .

Векторное произведение в (2) определяет векторный потенциал в точке наблюдения (xН,yН,zН) в форме:

^^{( J} ) = /',,. { [^ _y(z_H-z ) -M_z(y_H-y ^ ] } ^J + 4ЛК ^k                                ’

⁺ [ ^M z ⁽ x H ^- x r ) ^{- M} x ^{( z} H ^{- z} r ) ] ^{7 + [ M} x ⁽ У н ^- У т ) ^{- M} y ⁽ x H ^- x r ) ] k J }

С использованием известных параметров геомагнитного поля Земли и выражения (3) зависимость для напряженности ЛГП в точке наблюдения может быть определена:

^H A ⁽ xh , У н , ^z H ) = Й 3 ⁺ — ^rotA(. R J ) =

= """ T{ { ^[ 3 M x ⁽ x H ^- x r ) ^{+ 3(} x H ^- x r ) Г ^М У ^{( У} н ^- .Уг ) ⁺ M z ⁽ z H ^{- z} r ) ! ^-

4 R

- M x R ² + 4лR⁵H 3 ■ cos j ■ cos 6_M J i +[ 3 M_y ( y_H - y_r )² +

^{+ 3( у} н ^{- y} r ) [ ^M x ^{( x} H ^- x r ) ^{+ M} z ^{( z} H ^{- z} r ) ] ^{- M} y ^R 2 ⁺

+ 4лR⁵H з ■ cos j ■ sin 9_M J j + ^[ 3 M z ( zh - z r )² +

+3(zH - zr)[Mx ( xh - xr) + My (Ун - Уг )J- MzR 2 + +4rR 5 H 3 ■sin 7 J kJ где HЗ – напряженность МПЗ, θM,J – углы магнитного склонения и наклонения.

При относительном перемещении аномального ЛГП со скоростью V = Vxi + Vyj + Vzk в магнитной рамке и электри- ческом диполе возникают электродвижущие силы, создающие падения напряжений на сопротивлениях нагрузки.

В соответствии с законом индукции напряжение на сопротивлении нагрузки магнитной рамки пропорционально производной от напряженности изменяющегося аномального магнитного поля [3, с. 70]:

U (x, y, z, t) = Mxdbr (xH, Ун, zH, t) dt где ξM – коэффициент, зависящий от типа магнитной рамки.

Тогда, в зависимости от направления относительного перемещения аномального ГМП, можно из (5), (4) определить выражения для напряжений на сопротивлении нагрузки магнитной рамки ориентированной в соответствующих координатных осях в форме:

^Uxh ( t ) = W( x '' ^{U +} V x ' D ^{+ M} x ' G )

U ( t ) = w( у ’ ' U + V y ' ^D + ^M y ' G ) ’

U zh ( t ) = ^('z '' U + V z • D + ^M z • G )

где обозначено:

x ' = x о ⁺ Vt - x T ; y ' = y о ⁺ Vt - У т ; z ' = z о ⁺ Vt - z T ;

R = 7 ( x ')² + ( y ')² + ( z ')²;

f = M x V x + M y V y + m_zv_z ;

D = M x x ' + M _y y ' + M _z z ' ;

G = V x x ' + V y y ' + V_zz ' ;

U = F - 5 DGIR ²

На рис. 1 приведены рассчитанные по формулам (6) в среде MathCAD нормированные значения напряжения на нагрузке магнитной рамки ориентированной вдоль соответствующих координатных осей при перемещении ГМА вдоль координатной оси x со скоростью V _x =25 м⁄с.

Приведенные графики получены при смещении ГМА относительно магнитной рамки ∆y=70 м, ∆z=0 (рис. 1, а) и ∆y=70 м, ∆z=30 м (рис. 1, б).

области вектор напряженности поля (7) будет определяться магнитной составляющей (сторонней напряженностью поля E _ст ):

E — ( x , y , z ) = E — cm = V * x j* = V * X о н H =

= Ab { Г ³ D(V y Z '- V z y ') + ( M y V z - M z V y ) R ² +

4л- R

+ W ( V y sin j - V z cos j sin M_M ) ^— + [ 3 D ( V z x ' - V x z ') + ( M_zV_x - M_xV_z ) R ² + + W ( V z cos j cos M_M - V , sin j ) ^— + [ 3 D(V_zy' - V y x ') + ( M_zV y - M y V_z ) R ² +

+W(Vx cos j sin MM - Vy cos j cos вм)] k} где W=4πR5HЗ.

Напряжение на выходе несимметричного вибратора пропорционально производной по времени продольной (вдоль оси вибратора) составляющей напряженности электрического поля [3, с. 64] и определяется:

UE (t) = EE~ECcT (xH, yH, zH, t) dt где ξE – коэффициент пропорциональности, зависящий от типа дипольной антенны.

Для квазистатичного вибратора с использованием (8), (9) можно записать:

U xe ( t ) = TT E [ ( V y z ' - V z y')U + ( M y V z - M z V y ) G ] 4itR ^{5 L                                    J}

U ye ( t ) =       [ ( V z x ' - V x z ') U + ( M_zV x - M x V z ) G ] ■

47T ^R

U ze ( t ) = Tib [ ( V x y ' - V y x ') U + ( M x V y - M y V x ) G ] 4itR ^{5 L}                        z z j

Здесь использованы те же обозначения, что и в формуле (6).

На рис. 2 приведены рассчитанные по формулам (10) в среде MathCAD нормированные значения напряжения на нагрузке несимметричного вибратора ориентированного вдоль соответствующих координатных осей при перемещении ГМА вдоль координатной оси x со скоростью V _x =25 м⁄с . Приведенные графики получены при смещении ГМА относительно вибратора ∆y=70 м, ∆z=0 (рис. 1, а) и ∆y=70 м, ∆z=30 (рис. 1, б).

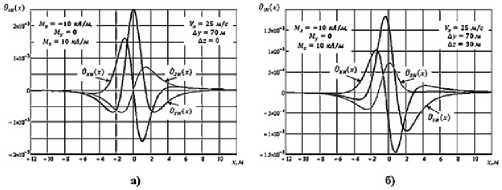
Рисунок 1. Нормированное значение напряжения на нагрузке магнитной рамки ориентированной вдоль соответствующих координатных осей

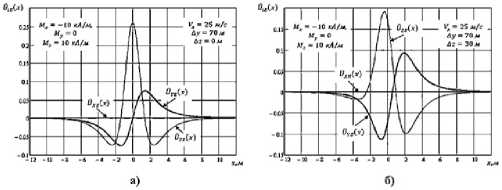
Рисунок 2. Нормированное значение напряжения на нагрузке несимметричного вибратора ориентированного вдоль соответствующих координатных осей

При относительном перемещении аномального ГМП на- ряду с магнитным полем существует и электрическое поле, напряженность которого в общем виде определяется зави- симостью:

—*

—             dA — —

E = - grad (ф) ---+ ( V x B )

dt где ф,A - скалярный и векторный электродинамические потенциалы, B = д0H - вектор магнитной индукции.

В отсутствие электрического поля в рассматриваемой

При расчете напряжений (6) на выходе рамки нормирование проводилось на величину , а для напряжений (10) на выходе несимметричного вибратора – на величину 3 ₀ /4 . При этом необходимо отметить, что для одинаковых кинематических условиях относительного перемещения ГМА уровень сигнала на выходе магнитной рамки может превышать уровень сигнала на выходе несимметричного вибратора примерно на 3…4 порядка.

Выводы. Реальные пространственно-временные структуры ГМА отличаются от рассмотренных значительно боль- шей неоднородностью, порождаемой множеством факторов их образования и относительным перемещением источников вблизи приемных антенн. Поэтому наводимые в антеннах помеховые сигналы, пропорциональные производной по времени аномального ЛГП, могут быть существенными. Кроме того многофакторное пространство ГМА может порождать контактные помехи радиоприему [4] в широком спектре частот.