Функционирование математической модели ошибок бесплатформенной инерциальной навигационной системы при одновременной навигации, динамическом построении и обработки данных многоструктурных систем управления в рамках разработки алгоритмов интегрированной системы навигации летательного аппарата с использованием GPS / ГЛОНАСС технологий

Simultaneous Location and Mapping (SLAM)

Интенсивное развитие методов и моделей одновременной навигации и построения электронных карт при решении актуальных задач управления и наведения для подвижных объектов различной природы приводит к необходимости вырабатывания и обоснования путей разрешения новых проблем построения информационно-аналитических систем управления как в условиях мониторинга значительных масштабов, обновления больших массивов геопространственных данных, так и преодоления запретных зон и других [1]. Синтез и обработка проблемно-ориентированных структур пространственных данных, к примеру, при динамическом построении маршрутов движения беспилотных летательных аппаратов (БПЛА), успешно осуществляется с применением технологий SLAM – оригинальной концепции, которая связывает два независимых процесса в непрерывный цикл последовательных вычислений, при этом результаты одного процесса участвуют в вычислениях другого процесса. Подход SLAM подразумевает также ряд новых методов, используемых роботами и БПЛА для построения карты в неизвестном пространстве или для обновления карты в заранее известном

пространстве с одновременным контролем текущего местоположения, состояния объекта и пройденного пути. Однако построение электронных карт маршрутов движения подвижных объектов не является достаточным для эффективного выполнения целевого предназначения сложного динамического объекта, в связи с чем выделяется актуальная фундаментальная проблема согласования данных методов управления движением и концепции SLAM для реализации мониторинга значительных масштабов при существенном ограничении возможностей обеспечения информационноаналитическими, коммуникационными и вычислительными ресурсами в современных условиях. Существенной проблемой в задаче построения электронных карт маршрутов движения подвижных объектов является учет ошибок БИНС.

Для вывода модели ошибок БИНС воспользуемся следующими векторными соотношениями.

• 1.    Уравнение ошибок построения вертикали и ориентации в азимуте:

j j j j     j

• er = er × ωМ - εМ + ∆ωМ ,        (1)

• 2.    Уравнение ошибок выработки скорости:

где j = х • z + а • j + в • к - вектор конечного поворота, представляющего собой совокупность трех элементарных поворотов на углы α (характеризует азимутальную ошибку БИНС), β и χ (ошибки построения вертикали); (jM - вектор угловой скорости географического                  трехгранника;

^s m = [ S - , ^s ум , ^£ zm ] ^T - вектор дрейфов гироскопов;

А 0 2 _M - вектор ошибок вычисления угловой скорости географического трехгранника.

А ^ м = — e r ^{х п} м + 5 a m + А < k

где n- - вектор перегрузок, записанный в проекциях на оси местной географической системы координат; 5a М = [5ax, 5a y, 5a z ]т - вектор смещения нулей акселерометров; Аak - вектор ошибок компенсации «вредных» ускорений.

Найдем компоненты вектора ошибок угловой скорости географического трехгранника А о м как разность между «расчетными» и истинными значениями. Представим в этих соотношениях «вычисленные» параметры движения в виде суммы «истинного» значения и малой ошибки. Пренебрегая величинами второго и более высокого порядка малости и вычисляя векторные произведения f х 0)_м и г х п_м , получаем следующую систему уравнений ошибок БИНС:

а = о - - в - о - - X + —-А V - +[ V z-  +О з cos ф ^-А ф - ^^ ф -А r - S y- ;

r          (r cos ф           )

АVV

\P = —®xM« + OyM X--x- + "^T А r - S zM rr

А VV

XL = ^O zM « ^{- O} yM ^{в +}-- ^Q З ^sm ф ^-А Ф-- ~ ^А r ^{- S} xM ;

rr

• А VxM = g0в • nyM - ga • nzM + ^xM - АakM;

• < А VyM = g0X - nzM - g0 в • nxM + 5a yM - А7-;

А VzM = g0a - nxM - g0X - nyM + SdyM - АakM•

Определим ошибки определения координат ф, X, h аналогичным образом. Получим для этих ошибок следующие уравнения:

~

Аф) = ф - ф = — - —^м = ~      r

V

АХ = X - X = —z^M r cos ф

Л7 7

V xM - V xM А _r rr ²

;

Vzm _ А V --—----- r cos ф r cos ф

\h = h—h = 7 -V =

^А ’^{1 h} h V yM V yM ^А V yM

VV

+ ^zM— Аф А r r cos² ф       r ² cos ф

Представим погрешности гироскопов и акселерометров БИНС следующим образом:

• -    Sm = -^m5x + ^M - 5 A - 5^ - ^_M - 5K_K + f z^- 5co_pk + f x^- 5(0_Tk + 5 э_й + ² f ^M{^zM 5о_д

Л-lVl             ZIVL x         ZIVL                    Lt         XIVL                                   Ut                      r              Lt                2

g 0         g 0

;

• -    ^SyM = ° zM • ⁵Ty - ⁵⁰тр - ° xM • ⁵ky - ° yM • 5 K p ⁺ f z^{- -} 5° pp ⁺ f f y^- - 4 5° _Tp ⁺ 5° zp ^{+ 2 f yM} 2 ^ z^{- 50} Hp ;

g 0         I g 0    )

• - ^S zM = ^O xM ^{- 5}kz - ^O xM ^{5 A} - ⁵⁰ tT - ^O zM ^{5 K} T ⁺ x^{- 5 5tO} p T ⁺ z^{- 5 50} rT ^{+ 5O} tT ⁺ ^x^M^^zM

g 0          g 0                   g 0

5 f xM =Ат _х + 5T x + 5 Q x - fxM ;

< 5 f yM = Ат у + 5т y + 5 Q y - f yM - 5 yx - f xM + 5 yz - f - ;

5fZM =Атг + 5тz + 5Qz - f- + 5zx - fx-, где 5fxM, 5fyM, 5fzM - ошибка определения кажущегося ускорения; дюрк, дюрр, ЗшрТ, Stork, Smrp, SrorT - отклонения скоростей ухода гироблоков (ГБ) из-за осевой и радиальной разбалансировки; SroTk, дготТ, дготр - случайные угловые скорости ухода ГБ из-за тяжения и осевой разбалансировки; StoHk, дгонр, §гонТ - составляющие случайной угловой скорости ухода из-за неравножесткости ГБ; §Кк, §КТ, §Кр - отклонение масштабного коэффициента по осям МГСК; Атх, Ату, Atz - отклонение среднего значения акселерометров; Six, дгу, Siz - случайные отклонения акселерометров; SQx,SQy,SQz - отклонения масштабных коэффициентов акселерометров; Szx, Syz, Syx - ошибки взаимной выставки акселерометров; STx, Skz, STy - ошибки выставки кинематического момента ГБ; SФх0, SФz0 - ошибки на-

~  е~  е~ чальной выставки ГБ в горизонт; 5отк, оотТ, осотр

- погрешности калибровки ухода ГБ вокруг осей МГСК; fxM, fyM, fzM - измеренные значения кажущегося ускорения; SA(0) - начальная погрешность определения азимута.

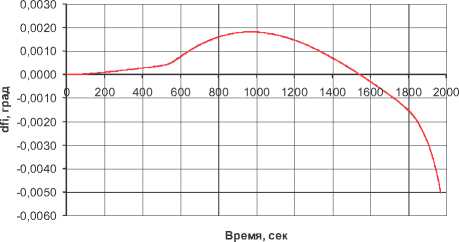
Приведенная модель ошибок БИНС использовалась в алгоритмах интегрированной комплексной навигационной системы летательного аппарата. Комплексирование осуществлялось с применением фильтра Калмана 25-го порядка по слабосвязанной схеме. Примерный вид ошибок определения координат и скорости как функции времени движения приведен на рис. 1. Видно, что сходимость фильтра Калмана обеспечивается с первых секунд движения. При этом точность навигации интегрированной системы определяется точностью спутниковой составляющей.

Имеющийся обширный научно-технический задел по разработке и реализации методов управления движением и наведением сложных динамических объектов не позволяет осуществлять мониторинг и анализ динамики их движения и поведения при одновременной навигации и существенных ограничениях информационно-аналитических, коммуникационных и вычислительных ресурсов. В условиях интенсивного развития многоструктурных систем управления БПЛА возникает проблема в совмещении методов управления движением и наведением летательного аппарата с имеющимися наработками в области геоинформа-ционных аналитических систем с целью совершенствования данных методов и анализа поведения летательного аппарата, включая различного рода ситуации в условиях преодоления запретных зон [2].

Изменение угла dfi

dfi,grad     dfi_FK

1,00

0,00

-1,00

-2,00

-3,00

-4,00

-5,00

-6,00

-7,00

Изменение dVx

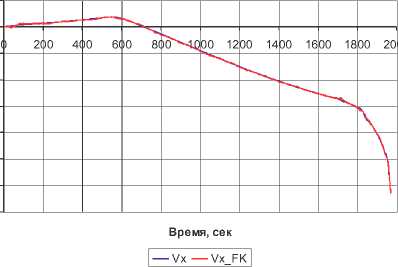
Рис. 1. Погрешности определения широты А ^ и составляющей скорости А V_x

В интересах обоснования путей разрешения проблем построения информационно-аналитических систем управления в условиях мониторинга значительных масштабов, обновления больших массивов геопространственных данных и эффективного выполнения целевого предназначения сложного динамического объекта с использованием методов и алгоритмов языка схем радикалов необходимо решить задачу синтеза методов управления и наведения при одновременной навигации, динамическом построении и обработки проблемно-ориентированных структур пространственных данных движения БПЛА посредством информационно-аналитических систем управления методов и моделей одновременной навигации и построения электронных карт при решении задач управления и наведения для подвижных объектов различной природы в сложных условиях мониторинга и преодоления запретных зон. В результате сравнительного анализа выделен ряд теоретических и экспериментальных методов и средств одновременной навигации, динамического построения карт и коррекции маршрутов движения для разработки комплексных навигационных систем в составе проблемно-ориентированной системы управления с целью мониторинга и анализа ситуаций с высокой степенью неопределённости в рамках концепции SLAM. Предложены комбинированные методы и алгоритмы управления и наведения БПЛА на всех участках полета, использующие сочетание энергетического подхода, свойства инвариантности динамических систем, программно-терминального принципа управления и модифицированного метода требуемых ускорений. Разработаны способы интеграции и комплексирования методов и алгоритмов управления и наведения с использованием оригинальной структуры данных на основе концепции SLAM для геоинформационных аналитических систем и усовершенствована математическая модель ошибок инерциальной навигационной системы в рамках разработки алгоритмов интегрированной системы навигации летательного аппарата. Таким образом, методы и алгоритмы наведения БПЛА на основе сочетания энергетического подхода, свойств инвариантности динамических систем, адаптивных манёвров, программно-терминального принципа управления и метода требуемых ускорений, методы идентификации, адаптации, когнитивных и нейросетевых технологий в приложении к новым возможностям технологий SLAM могут быть использованы автономными транспортными средствами для создания карты в незнакомой обстановке (без априорного знания), или обновления карты в известной среде (с априорного знания из данной карте), и одновременного отслеживания своего текущего местоположения [3].

Стремительное развитие авиационных и ракетно-космических технологий влечет за собой появление новых типов летательных аппаратов и систем, открывает новые возможности при решении ими функциональных задач. В результате такого развития ощущается потребность в создании надежных, компактных и интеллектуальных навигационных комплексов, имеющих относительно низкую стоимость по сравнению с традиционными платформенными инерциальными системами (ИНС) [4, 5]. В настоящее время основным путем создания таких систем является использование глобальных навигационных спутниковых систем GPS/ГЛОНАСС в сочетании с БИНС. Опыт разработчиков показывает, что наиболее приемлемыми для таких объектов управления являются слабо-, жестко- и глубоко интегрированные навигационные системы. Так, переход от «чисто инерциальной» к слабо связанной схеме позволяет существенно повысить точность за счет постоянной коррекции БИНС по данным спутниковой навигационной системы (СНС). Использование жестко связанной схемы дополнительно позволяет улучшить качество слежения за спутниковыми сигналами и снизить время восстановления после срыва слежения. Организация системы по глубоко интегрированной схеме позволяет реализовать преимущества, описанные ранее, при меньших массогабаритных характеристиках и меньшем энергопотреблении, что важно для летательных аппаратов (ЛА) с дефицитом энергетических ресурсов. Необходимо отметить, что жестко- и глубоко связанные схемы не всегда оказываются функционально надежными и могут не обеспечить требуемое качество навигации при длительных перерывах в получении информации от СНС (например, при постановке помех), поэтому в настоящем работе рассматривалась слабосвязанная интегрированная инерциальноспутниковая система как обеспечивающая (по совокупности показателей) более высокую точность, устойчивость слежения и надежность информационного обеспечения по сравнению с другими схемами комплексирования.

В ходе исследований предполагалось, что точность СНС является достаточной для решения ЛА его функциональных задач, поэтому модель погрешностей СНС рассматривалась в самом общем виде – на уровне задания ошибок определения координат и скорости без детализации причин их возникновения. Основное внимание уделялось определению ошибок БИНС и алгоритмам оптимальной фильтрации, обеспечивающим работу интегрированной навигационной системы. В числе погрешностей ИНС рассматривались инструментальные ошибки гироскопов и акселерометров, а также ошибки выставки и ввода начальных условий работы системы. Другие составляющие погрешностей считались пренебрежимо малыми. Инструментальные погрешности ИНС моделировались постоянными составляющими, компонентами, зависящими от перегрузок, а также случайными величинами ошибок акселерометров и параметров, описывающих уходы гироблоков. Ошибки выставки и ввода начальных условий задавались случайными переменными.

В системе реализовывался расширенный фильтр Калмана для 25-мерного вектора состояния. Вектор возмущений системы имел размерность, равную 21. Спутниковая информация включала шесть параметров: координаты и компоненты скорости ЛА, пересчитанные в географическую систему. Для фильтра Калмана при плохой сходимости оценок предусмотрена работа в так называемом режиме ε-механизации. Такой режим в ряде случаев обеспечивает лучшие характеристики сходимости оценок. В результате работы фильтра вычислялась оценка текущих ошибок БИНС в определении координат, скоростей, а также оценки составляющих погрешностей ее акселерометров и гироскопов. На основе полученных оценок корректировались показания БИНС и ее измерительных элементов.

Чтобы сформировать требуемую траекторию полета, обладающую заданными свойствами, системе управления ЛА должны быть заданы законы измерения координат и компонент скорости в какой-либо системе координат. Конкретный вид связи, накладываемой на движение центра масс, и определяющей траекторию движения, определяет метод наведения. Для достижения требуемой эффективности применения ЛА в терминальной точке требовалось обеспечить заданное значение угла наклона траектории, а также величину скорости, лежащей в приемлемом диапазоне. Траектория полета, обладающая указанными свойствами, была получена при использовании модифицированного метода наведения по требуемым ускорениям.

Результаты моделирования работы интегрированной системы навигации показали, что точность определения координат и составляющих вектора скорости определяется точностью спутниковой подсистемы. Сходимость фильтра Калмана при получении оптимальных оценок указанных параметров обеспечивается в течение нескольких секунд. Несколько хуже оказались характеристики сходимость фильтра при расчете систематических составляющих погрешностей БИНС (процесс получения оценок некоторых параметров затягивался до 100-140 с).

Выводы: сопряжение БИНС с СНС позволяет уменьшить систематические погрешности ИНС приблизительно на порядок, если удается обеспечить продолжительность непрерывного сеанса получения измерительной информации по спутниковому каналу в течение 150 и более секунд.