Fuzzy entropy based MOORA model for selecting material for mushroom in viet nam

Published Online September 2019 in MECS DOI: 10.5815/ijieeb.2019.05.01

• I.    Introduction

  King oyster mushrooms and Pleurotus sajor-caju are delicious, nutritious foods and bring great value to tropical countries. Materials for growing mushrooms in tropical countries are diverse such as sawdust, rice husk, rice bran, bagasse, straw, etc… By 2013, Sharma et al. [5] also confirmed that rice straw is a substrate for abalone mushroom production with higher yield than wheat straw and sawdust. In 2015, Le et al. [3] studied and pointed out that although the productivity of Pleurotus sajor-caju grown on rice husk is not the highest, the mushroom grows fast, giving the early harvest. In 2016, Nguyen et al. [1] studied the mixing formula of the proportions of raw materials including rice straw, corn cob, sawdust, rice bran and CaCO 3 . They show that the formula mixed with 40% rice straw + 20% corn cob + 19% sawdust + 20% rice bran + 1% CaCO 3 will result in the biological

performance of King oyster mushroom originating from Japan growing in Vietnam is the highest. Studies also analyze the characteristic properties of mushroom, such as the diameter of mushroom caps, fungal stem height and biological efficiency. Experimental studies also analyze the characteristic properties of mushroom, such as diameter of mushroom caps, fungal stem height and biological efficiency. From there, conclude the mixing formula, or mushroom planting materials for the best results. These studies also indicate infection rates when using fungal growing materials, or different mixing formulations. But the incidence of this disease should be studied in parallel with the characteristics of the fungus or biological performance as mentioned above so that there is an evaluation of the best ingredients or mixing formula for mushroom cultivation. Then we will have the multi-criteria decision making (MCDM) problem, i.e. selecting the best options on the set of alternatives based on the set of criteria. In the study of growing mushrooms, selecting the right materials will give the best results while taking advantage of the diverse available local materials. There are many different optimization techniques that have been used to select the most suitable material source for design or farming. For instance, Analytical Hierarchy Process (AHP) [6], TOPSIS [7, 14], Gray relational analysis (GRA) [8], VIKOR method [9], MOORA method [2, 4, 10] and MCDM method [11, 13, 19-21,24], etc. Because in evaluating the selection of ingredients or mixing formulations used for mushroom cultivation, the above analysis has the infection rates of fungi brought by the ingredients. We consider the incidence of this disease to be a non-profit criterion, in addition to other criteria such as biological productivity as a benefit criterion. That is, decision making here has both benefits and non-benefit criteria, they can conflict with each other.

At the same time, the obtained data may be inaccurate due to the measurement, or the recorded report. Fuzzy logic [12] is an effective tool for solving inaccurate, uncertain data problems. Therefore, in this paper, we propose the use of fuzzy MOORA (FMOORA) and fuzzy MCDM (FMCDM) methods to select the most effective mushroom growing ingredients or the most effective mushroom mixing recipes. In this paper, we use the fuzzy method Left-Right to construct the membership function for fuzzy sets from the set of real numbers as shown in Fig.1 and Fig.2. The weights are also built based on the entropy function, because the entropy function is verified to evaluate information as well. In this paper, we also used fuzzy MCDM model with Euclidean distance measurement to evaluate mushroom selection. We then compared the results to the experimental results. The results of the article also contribute to reinforce the conclusion of experimental results. Moreover, the experimental results independently consider the criteria of benefit and non-benefit criterion, they attach importance to the benefit criteria first, then consider the criteria of no benefit. In our proposed models using theoretic of fuzzy set, we combined to use both consider group of benefits and group of non-benefit criteria simultaneously. That is the outstanding contribution of this article to select mushroom planting materials. The rest of the article is organized as follows: Section 2, we reiterate the methodology of FMCDM, FMOORA methods. Section 3, we apply the methods mentioned in section 2 to the numerical examples already in references [1, 3]. The conclusion is shown in section 4.

• II.    Methodology

• 2.1    The FMOORA method

Fuzzy multi criteria decision making method (FMCDM) provides the ranking solution to find out the best quantitative solution from a set of alternatives A = {A, A..... A } based on the set of criteria 12    m

C = {CpC2,...,C} . In which each criterionc has a weight wy(j = 1,2,...,n) such that ^w = 1 . In this j=1

paper, we applied entropy method for the FMCDM because it provides high accuracy in determination of weight of the criteria in the model. A FMCDM problem can be expressed in fuzzy decision matrix D = I d I ij m x n as follows

C1       Cn

^Am  L ^dm1  • "  ^dmn _

Fuzzy Multi Objective Optimization on the Basis of Ratio Analysis (FMOORA) method [2] is presented with these following steps.

Step 1 . Normalization decision matrix

In this step, we construct the fuzzy decision making matrix using eq.(1) or eq. (2)

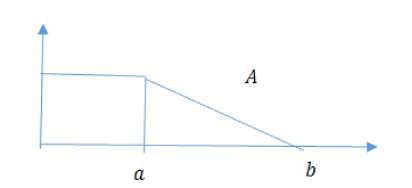
Fig.1. The membership function of fuzzy set A

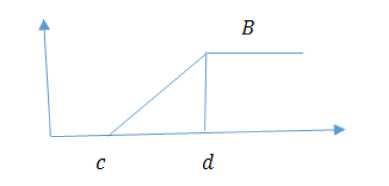
Fig.2. The membership function of fuzzy set B

The membership function [12] of Л or B as

1 if x < a or

M a ^{( x} ) =

b — x b - a

if a < x < b if x > b

if x <  c

M b ^{( x} ) = *

x — c d — c

1

if c <  x <  d

if x >  d

This step can be ignored if D is the fuzzy decision matrix.

Step 2 . Calculate the fuzzy entropy [15] e of each

criteria C ■ for all j = 1,2,..., n.

j

m

Step 3 . Calculate the weight w of each criteria C for all j = 1,2,..., n .

w j =

¹ - e j

n

Z(1 - j j=1

Step 3 . Compute the distance of each alternative to the

*

perfect option P as follows

Step 4 . Calculate the weighed normalized decision matrix W = Г W ,1

L У _lm x n

Wj = wjx dij(5)

Step 5 . Compute

P = ИZ j.B Wj and

^B zjeNb'p where B is the set of benefit criteria and NB is the set of all non-benefit criteria, for all i = 1,2,..., m.

Step 6. Compute the relative weight of each alternative

Q i = P - R i

for all i = 1,2,..., m .

Step 7. Ranking the alternatives AA     if

Q_k >  Q. for all i , k = 1,2,..., m .

• 2.2 . The FMCDM method based on the distance of fuzzy sets

The fuzzy multi criteria decision making (FMCDM) based on distance of fuzzy sets is presented with these following steps.

Step 1 . Normalization decision matrix

In this step, we construct the fuzzy decision making matrix using eq.(1) or eq. (2).

This step can be ignored if D is the fuzzy decision matrix.

Step     2 .     Chose     the    perfect    option

*

P = ⁽ P 1 ,P 2 ,...,P n ) where P j = ¹ if C j is the benefit criterion and pj = 0 if C. is the non-benefit criterion, for all j = 1,2,..., n .

d ( A , A *) =

n

J- z ⁽ d ij - p, )

V ⁿ j = 1

Step 4 . Ranking the alternatives AA if d ( A , A *) <  d ( A , A *) for all i , k = 1,2,..., m .

• III.    Case Studies

In order to demonstrate the effectiveness of the proposed methods (in section 2), we consider numerical examples in the selection of mushroom cultivation options in Vietnam and compare them with experimental results.

Example 1 [1]. To grow King oyster mushroom, we often use straw, corn cob, sawdust, rice bran, CaCO 3 . They are blended according to certain ratios, Nguyen et al. [1] consider each mixing formula as an alternative.

Alternative A 1 : 40% straw + 30% sawdust + 0% rice bran+ 1% CaCO 3

Alternative A2: 40% straw + 27% sawdust + 5% rice bran+ 1% CaCO3

Alternative A3: 40% straw + 25% sawdust + 10% rice bran+ 1% CaCO3

Alternative A4: 40% straw + 22% sawdust + 15% rice bran+ 1% CaCO3

Alternative A5: 40% straw + 20% sawdust + 20% rice bran+ 1% CaCO3

Alternative A₆: 40% straw + 17% sawdust + 25% rice bran+ 1% CaCO 3

corn cob + 29% corn cob + 27% corn cob + 24% corn cob + 22% corn cob + 19% corn cob + 17%

Evaluate the impact of growing raw materials on the growth and productivity of king oyster mushrooms. We consider the criteria ( C ) the diameter of the mushroom caps (mm), ( C ) the diameter of the mushroom stalks (mm), ( C ) the length of the mushroom stalks (mm), ( C ) b iological productivity (%) and ( C ) the infection rate (%). In there, Criteria C , C , C , C are criteria for benefits, and the C criterion is a non-benefit criterion. Data of the impact of growing raw materials on the growth and productivity of king oyster mushrooms [1] indicates the table 1.

Table 1. Effect of mixing formula on fruit size, biological productivity and infection rate of king oyster mushroom [1]

	C 1	C 2	C 3	C 4	C 5
A 1	27.7	20.1	96.5	33.5	6.6
A 2	35.2	24.3	102.6	41.7	7.1
A 3	40.4	27.9	120.1	46.8	8.3
A 4	46.8	30.4	132.4	51.4	9.4
A 5	50.4	32.6	146.2	59.4	9.9
A 6	50.3	32.5	143.4	59.1	10.8

• •    Using the FMOORA method

Now, we present the process of the proposed method for evaluating the impact of growing raw materials on the growth and productivity of king oyster mushrooms.

Step 1. Because of the C , C , C criteria are not normalized, we need to bring it to the normalized fuzzy form by using the eq.(2). Specially, criterion C we using the eq.(2) with c = 20, d = 60 ; criterion C2 we using the eq.(2) with c = 20, d = 40 and criterion C3 we using the eq.(2) with c = 50, d = 150 Then, we get the fuzzy decision matrix of effecting of mixing formula on fruit size, biological productivity and infection rate of king oyster mushroom as see in Table 2.

Step 2 : Using the eq.(3) we get the entropy of each criteria (Table 3)

Steep 3 . Using the eq.(4) we get the weight of each criteria (Table 3)

Step 4 . Calculate the weighed normalized decision matrix W = F w 1 by using the eq.(5) as see in Table 4.

L j J m x n

Step 5. Compute P and R for all i = 1,2,...,6, see in Table 5.

Step 6 . Compute Q for all i = 1,2,...,6, see in Table 5

Step 7 . Ranking alternatives, see in Table 5.

Table 2. The fuzzy decision matrix king oyster mushrooms

	C 1	C 2	C 3	C 4	C 5
A 1	0.7925	0.005	0.465	0.335	0.066
A 2	0.38	0.215	0.526	0.417	0.071
A 3	0.51	0.395	0.701	0.468	0.083
A 4	0.67	0.52	0.824	0.514	0.094
A 5	0.76	0.63	0.962	0.594	0.099
A 6	0.7575	0.625	0.934	0.591	0.108

Table 3. The weight of criteria in Example 1

	C 1	C 2	C 3	C 4	C 5
Entropies	0.5977	0.5393	0.4771	0.6754	0.2937
Weights	0.1665	0.1906	0.2164	0.1343	0.2922

Table 4. The fuzzy weighed normalized decision matrix king oyster mushrooms

	C 1	C 2	C 3	C 4	C 5
A 1	0.0321	0.0010	0.1006	0.0450	0.0193
A 2	0.0633	0.0410	0.1138	0.0560	0.0207
A 3	0.0849	0.0753	0.1517	0.0629	0.0243
A 4	0.1116	0.0991	0.1783	0.0690	0.0275
A 5	0.1265	0.1201	0.2082	0.0798	0.0289
A 6	0.1261	0.1191	0.2021	0.0794	0.0316

Table 5. The results of P i , R i and Q i for ranking of alternatives

	Pi	Ri	Q i	100 X   Q max Qi	Ranking
A 1	0.1786	0.0193	0.1593	31.51	6
A 2	0.2741	0.0208	0.2533	50.1	5
A 3	0.3748	0.0243	0.3505	69.32	4
A 4	0.4580	0.0275	0.4305	85015	3
A 5	0.5345	0.0289	0.5056	100	1
A 6	0.5267	0.0315	0.4952	97.93	2

This result indicates that A is the best option. It is also consistent with the experimental results shown in [1]. But in [1], the authors ranked mainly based on the four original criteria which are only criteria of benefit, without considering the non-benefit criteria C . In many cases, infection rates can affect the final profit of mushroom cultivation. Therefore, the use of the FMOORA decisionmaking model in assessing the selection of options on which there are conflicting attributes is meaningful.

• •    Using the FMCDM method based on the distance of fuzzy sets

Step 1 . The normalization decision matrix

In this step, we implement as in the FMOORA method and the normalization decision matrix obtained as in Table 2.

Step 2 . Chose the perfect option P * = (1,1,1,1,0)

Step 3 . Compute the distance of each alternative to the *

perfect option P . The results are shown in the Table 6.

Step 4 . Ranking the alternatives AA if

d ( A_k , A *) < d ( A , A *) for all i , k = 1,2,..., m , see Table 6.

In this method, we also see that that Л5 is the best option. It is also consistent with the experimental results shown in [1]. Figure 3 shows the ranking results using FMOORA, FMCDM and experimental methods.

Table 6. Ranking of alternatives in the example 1.

	A 1	A 2	A 3	A 4	A 5	A 6
d ( A i , A *)	0.6892	0.5604	0.4439	0.3508	0.2722	0.2767
Ranking	6	5	4	3	1	2

Rank

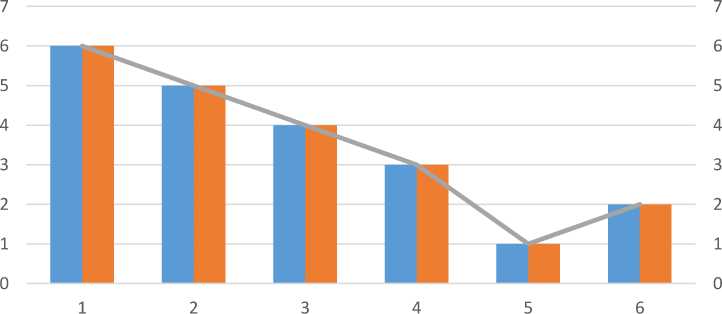
MOORA      FMCDM      Experiment

Fig.3. The ranking results using FMOORA, FMCDM and experimental methods in example 1

Example 2 [3]. Pleurotus sajor-caju is a popular and valuable mushroom in tropical countries. Le et al.[3] studied the effects of raw materials (alternatives) such as sawdust ( A ) , bagasse ( A ) , straw ( A ) , rice husk ( A ) and coco-peat ( A ) on biological productivity and mushroom quality to replace used sawdust.

The tracking indicators (criteria) include:

• -    ( C ) s peed of developing the length of silk thread (cm/day).

• -    ( C ) t ime of silage covered with silage of treatments (days): the number of days from the time of inoculation to the time when silk is fully covered with all the embryos of the experiment.

• -    ( C ) s tarting time for harvesting: from the start of irrigation to pick up mushrooms until there is 50% of the bags in each repeat of the treatments for harvesting.

• -    ( C ) b iological efficiency (%): productivity of fresh mushrooms / kg of dry matter.

• -    ( C )t he rate of embryos infected with mold (%) in the substrate

• - ( C )t he number of infected embryos on each

treatment.

• -    ( C )t he length of time for harvest is long: since 50% of the bags of the treatments are harvested until 50% of the bags cannot be harvested anymore.

• -    ( C )t he amount of mushroom collected on each bag (g/bag)

• -    ( C )d ry weight of fungi on treatments: mushrooms are dried to constant weight and calculated the dry weight of mushrooms on the treatments.

In which C is the non-benefit and the other criteria are benefit.

The relation between of alternatives and criteria is shown in the Table 7.

Table 7. The relation between of alternatives and criteria in example 2

	C 1	C 2	C 3	C 4	C 5	C 6	C 7	C 8	C 9
A 1	0.92	24.3	11.1	33.9	5.6	3.1	36.6	305.2	10.2
A 2	0.85	27.7	12.6	39.9	11.3	3.2	37.3	359.2	10
A 3	0.78	30.6	13	24.9	22.2	3	26.6	224.2	8.4
A 4	1.4	16.7	10.4	34	11.1	4.1	36.8	288.8	8.8
A 5	0.8	28	13	11	27.8	2.1	32.7	99.1	8.5

• •    Using the FMOORA method

Step 1 . Because of the criteria C , C , C , C , C and C  are not normalized. For the benefit criteria

C, C  and C having the better if their values are higher; for the non-benefit criteria C, C C having the better if their values are lower. So we need to bring it to the normalized fuzzy form by using the eq.(2). Specially, for criterion C we using the eq.(2) with c = 0.7, d = 1.5; for criterion C2 we using the eq.(1) with a = 15, b = 35; for criterion C3 we using the eq.(1) with a = 10, b = 55; for criterion C6 we using the eq.(2) with c = 2, d = 5; for criterion C7 we using the eq.(1) with a = 30, b = 40; for criterion C6 we using the eq.(2) with c = 80, d = 360; Then, we get the fuzzy decision matrix of effecting of mixing formula on fruit size, biological productivity and infection rate of king oyster mushroom as see in Table 8.

Step 2 : Using the eq.(3) we get the entropy of each criteria (Table 9)

Step 3 . Using the eq.(4) we get the weight of each criteria (Table 9)

Step 4 . Calculate the weighed normalized decision matrix W = ^ Wy J by using the eq.(5) as see in Table 10.

Step 5 . Compute P and R for all i = 1,2,...,5, see in Table 11.

Step 6 . Compute Q_t for all i = 1,2,...,5, see in

Table 11

Step 7 . Ranking alternatives, see in Table 11.

Table 8. The fuzzy decision matrix king oyster mushrooms

	C 1	C 2	C 3	C 4	C 5	C 6	C 7	C 8	C 9
A 1	0.2750	0.535	0.78	0.339	0.056	0.3667	0.34	0.8043	0.102
A 2	0.1875	0.365	0.48	0.399	0.113	0.4	0.27	0.9971	0.1
A 3	0.1	0.22	0.4	0.249	0.222	0.3333	0.34	0.515	0.084
A 4	0.875	0.915	0.92	0.34	0.111	0.7	0.32	0.7457	0.088
A 5	0.125	0.35	0.4	0.11	0.278	0.0333	0.73	0.0682	0.085

Table 9. The weight of criteria in Example 1

	C 1	C 2	C 3	C 4	C 5	C 6	C 7	C 8	C 9
Entropies	0.4299	0.5624	0.5688	0.5724	0.4075	0.5447	0.6151	0.4045	0.3063
Weights	0.1242	0.0954	0.094	0.0932	0.1291	0.0992	0.0839	0.1298	0.1512

Table 10. The fuzzy weighed normalized decision matrix in example 2

	C 1	C 2	C 3	C 4	C 5	C 6	C 7	C 8	C 9
A 1	0.0342	0.0510	0.0733	0.0316	0.0072	0.0364	0.0285	0.1044	0.0154
A 2	0.0233	0.0348	0.0451	0.0372	0.0146	0.0397	0.0227	0.1294	0.0151
A 3	0.0124	0.0210	0.0376	0.0232	0.0287	0.0331	0.0285	0.0668	0.0127
A 4	0.1088	0.0873	0.0865	0.0317	0.0143	0.0694	0.0269	0.0968	0.0133
A 5	0.0155	0.0334	0.0376	0.0103	0.0359	0.0033	0.0612	0.0089	0.0129

Table 11. The results of P , R and Q for ranking of alternatives

	P i	R i	Q i	100 X   Q i max Qi	Ranking
A 1	0.3748	0.0072	0.3676	72.61	2
A 2	0.3473	0.0146	0.3327	65.72	3
A 3	0.2354	0.0287	0.2067	40.83	4
A 4	0.5206	0.0144	0.5062	100	1
A 5	0.1830	0.0358	0.1472	29.06	5

In example 2, we see that the biological efficiency of using rice husk ( A ) material is not the highest ( C ) , the rate of infection is not the lowest ( C ) . h owever , when considering the overall evaluation criteria, it gives the highest ranking results. This is worthy of consideration for research to implement practical applications in Vietnam because rice husk materials are abundant.

• •    Using the FMCDM method based on the distance of fuzzy sets

Step 1 . The normalization decision matrix

In this step, we implement as in the FMOORA method and the normalization decision matrix obtained as in Table 8.

Step     2 .     Chose    the    perfect    option

P * = (1,1,1,1,0,1,1,1,1)

Step 3 . Compute the distance of each alternative to the

*

perfect option P . The results are shown in the Table 12.

Step  4 .  Ranking the alternatives AA if

d(A, A*) < d(A, A*) for all i,k = 1,2,...,5.

In this method, we also see that that Л4 is the best option. It is also consistent with the experimental results shown in [3]. Figure 4 shows the ranking results using FMOORA, FMCDM and experimental methods.

Table 12. Ranking of alternatives in the example 1.

	A 1	A 2	A 3	A 4	A 5
d ( A i , A *)	0.5688	0.6156	0.6949	0.4626	0.7550
Ranking	2	3	4	1	5

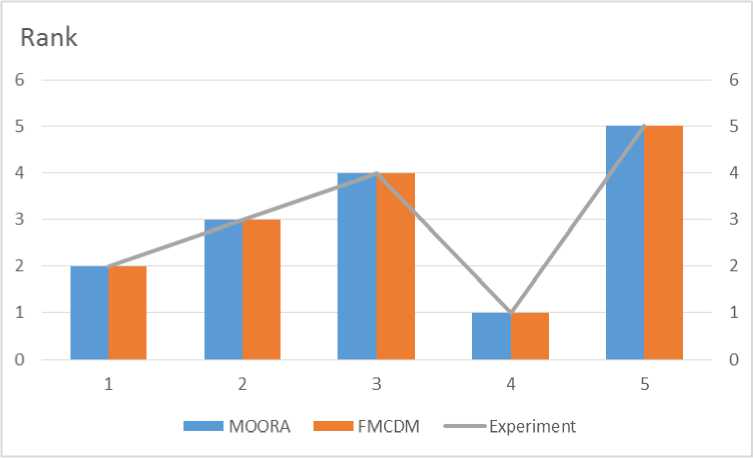
Fig.4. The ranking results using FMOORA, FMCDM and experimental methods in example 1

• IV. Conclusion

In this paper, we apply fuzzy MOORA and fuzzy MCDM methods to evaluate the selection of mushroom growing materials or the best options for mushroom cultivation. These methods are suitable for multi-criteria decision-making problems, especially for problems with evaluation criteria sets that may conflict with each other. The results obtained in the methods used in this paper are also consistent with the previously published experimental methods. As we see in example 1, changing components in the right proportion can affect mushroom yield, but if too much change may not yield good results. In example 2, we also consider the incidence of infection along with other criteria to evaluate the best mushroom planting material in the Mekong Delta, Vietnam. In the future, we will apply these methods to the problem of selecting other materials to serve the production process. As well as understanding fuzzy MOORA and fuzzy MCDM models in intuitionistic fuzzy sets and other measures to apply to practical problems such as decision making in health, selecting suppliers and choosing choose investment policy etc. At the same time, we also studied other methods of multi-criteria decision making so that we can compare the evaluation to select the right optimal conclusion. In addition, we will consider studying these models in such directions as using the correlation of intuitionistic fuzzy set [25 -26], Support-intuitionistic fuzzy set [17], Support – neutrosophic set

[18], the rough fuzzy set [16], and some other directions [27-29].

Acknowledgements

We would like to thank the financial support of the Vietnam - Belgium project, Vietnam National University of Agriculture code T2016-10-16-VB.

Refrences

• [1]    TBT Nguyen, XN Ngo, TT Nguyen, DA Tran, XC Nguyen, VG Nguyen and TD Tran (2016) Evaluating the Growth and Yield of King Oyster Mushroom (Pleurotus eryngii (DC.:Fr.) Quél) on Different Substrates. Vietnam J.Agri.Sci. 2016, Vol. 14, No. 5: 816-823.

• [2]    Brauers WKM (2004). Optimization methods for a stakeholder society. A revolution in economic thinking by multi-objective optimization. Boston: Kluwer Academic Publishers; 2004.

• [3]    VT Le, TNM Nguyen and VD Mai (2015). Effects of some potential agro-based wastes in Mekong Delta on the growth of Pleurotus sajorcaju, Tạp chí khoa học Đại học Cần thơ, 39: 36-43.

• [4]    Karande P and Chakraborty S (2012). Application of multi-objective optimization on the basis of ratio analysis (MOORA) method for materials selection. Materials & Design , 37 , 317-324.

• [5]    Sharma S., Yadav R.K.P. and C.P. Pokhrel (2013). Growth and yield of oyster mushroom (Pleurotus ostreatus) on different substrates. Journal on New Biological Reports 2(1): 03-08.

• [6]    Kiong, S. C., Lee, L. Y., Chong, S. H., Azlan, M. A., Nor, M., & Hisyamudin, N. (2013). Decision making with the analytical hierarchy process (AHP) for material selection in screw manufacturing for minimizing environmental impacts. In Applied Mechanics and Materials 315: 57-62.

• [7]    Mayyas, A., Omar, M. A., & Hayajneh, M. T. (2016). Eco-material    selection using fuzzy TOPSIS

method. International Journal    of    Sustainable

Engineering , 9 (5), 292-304.

• [8]    Jayakrishna, K., & Vinodh, S. (2017). Application of grey relational analysis for material and end of life strategy selection with multiple criteria. International Journal of Materials Engineering Innovation , 8 (3-4), 250-272.

• [9]    Jahan, A., Mustapha, F., Ismail, M. Y., Sapuan, S. M., & Bahraminasab, M. (2011). A comprehensive VIKOR method for material selection. Materials & Design , 32 (3), 1215-1221.

• [10]    Gadakh, V. S., Shinde, V. B., Khemnar, N. S., & Kumar, A. (2016, December). Application of MOORA Method for Friction Stir Welding Tool Material Selection. In Techno-Societal 2016, International Conference on Advanced Technologies for Societal Applications (pp. 845-854). Springer, Cham.

• [11]    Chakraborty, S., & Chatterjee, P. (2013). Selection of materials using multi-criteria decision-making methods with minimum data. Decision Science Letters , 2 (3), 135148.

• [12]    Zadeh, L. A. (1965). Fuzzy sets. Information and control , 8 (3), 338-353.

• [13]    Petković, D., Madić, M., Radovanović, M., & Janković, P. (2015). Application of Recently Developed MCDM Methods for Materials Selection. In Applied Mechanics and Materials Vol. 809, pp. 1468-1473.

• [14]    Bhowmik, C., Gangwar, S., Bhowmik, S., & Ray, A. (2018). Selection of Energy-Efficient Material: An Entropy–TOPSIS Approach. In Soft Computing: Theories and Applications (pp. 31-39). Springer, Singapore.

• [15]    Al-Sharhan, S., Karray, F., Gueaieb, W., & Basir, O. (2001). Fuzzy entropy: a brief survey. In 10th IEEE International Conference on Fuzzy Systems.(Cat. No. 01CH37297) (Vol. 3, pp. 1135-1139). IEEE.

• [16]    Nguyen, X. T., & Nguyen, D. D. (2014). Rough fuzzy relation on two universal sets. International Journal of Intelligent Systems and Applications , 6 (4), 49-55.

• [17]    Nguyen, X. T. (2015). Support-intuitionistic fuzzy set: a new concept for soft computing. International Journal of Intelligent Systems and Applications , 7 (4), 11-16.

• [18]    Thao, N. X., Smarandache, F., & Dinh, N. V. (2017). Support-Neutrosophic Set: A New Concept in Soft Computing. Neutrosophic Sets Syst , 16 , 93-98.

• [19]    Van Dinh, N., & Thao, N. X. (2018). Some measures of picture fuzzy sets and their application in multi-attribute decision making. Int. J. Math. Sci. Comput.(IJMSC) , 4 (3), 23-41.

• [20]    Le, N. T., Van Nguyen, D., Ngoc, C. M., & Nguyen, T. X. (2018). NEW DISSIMILARITY MEASURES ON PICTURE      FUZZY      SETS      AND

APPLICATIONS. Journal of Computer Science and Cybernetics , 34 (3), 219-231.

• [21]    Nguyen, X. T. (2018). Evaluating Water Reuse Applications under Uncertainty: A Novel Picture Fuzzy Multi Criteria Decision Making Medthod. International Journal of Information Engineering and Electronic Business , 10 (6), 32-39.

• [22]    Nguyen, X. T., Nguyen, V. H., & Garg, H (2017)

Exponential similarity measures for Pythagorean fuzzy sets and their applications to pattern recognition and decision-making process. Complex & Intelligent Systems , V5 (2),217-228.

• [23]    Thao, N. X., & Smarandache, F. (2018). Divergence Measure     of     Neutrosophic      Sets     and

Applications. Neutrosophic Sets and Systems , 142-152.

• [24]    Nhung L.T. and Nguyen.X. T (2019) A Novel MultiCriteria Decision Making Method for Evaluating Water Reuse Applications under Uncertaint. Vietnam Journal of Agricultural Sciences, V1(3), 230-239.

• [25]    Thao, N. X., Ali, M., & Smarandache, F. (2019). An intuitionistic fuzzy clustering algorithm based on a new correlation coefficient with application in medical diagnosis. Journal of Intelligent & Fuzzy Systems , Vol36(1), 189-198.

• [26]    Xuan Thao, N. (2018). A new correlation coefficient of the intuitionistic fuzzy sets and its application. Journal of Intelligent & Fuzzy Systems , V35(2), 1959-1968.