Fuzzy Stability and Synchronization of New 3D Chaotic Systems

Published Online October 2014 in MECS

Control of complex irregular dynamics has evolved as one of the central issues in applied nonlinear science during the last decade. Nowadays the notion of chaos control involving stabilization of unstable periodic or stationary states in nonlinear dynamic systems has been extended to a much wider class of problems. Since the discovery of chaos synchronization introduced in [1], there have been tremendous interests in studying the synchronization of chaotic systems. Recently, much research on the fuzzy model-based designs to stability and synchronization for chaotic systems have been carried out based on Takagi–Sugeno (T–S) fuzzy models [2–4]. In [5], a fuzzy model-based designs for Chen’s chaotic stability and synchronization have been proposed. Based on the fuzzy hyperchaotic models, simpler fuzzy controllers have been designed for synchronizing hyperchaotic systems in [6]. In [7], a novel IMRAFC for a class of nonlinear chaotic systems subject to disturbances was proposed. A robust model reference fuzzy controller and the adaptation laws for the identification system were derived using an appropriate Lyapunov function. [8] have considered the problem of synchronizing a class of uncertain nonlinear systems by using adaptive fuzzy sliding mode control technique. In [9], authors have considered the robust stabilization and synchronization problems for nonlinear energy resource systems based on T-S fuzzy model. By designing the fuzzy state-feedback controllers, several sufficient conditions have been obtained to ensure the stability, robust stability and synchronization of nonlinear energy resources systems, respectively. A new adaptive interval type-2 fuzzy neural network (FNN) control for chaos synchronization between two different chaotic systems was proposed to handle the training data corrupted by noise or rule uncertainties involving external disturbances [10]. By investigating synchronization of chaotic systems, the structure of drive-response lag synchronization for fuzzy chaos system based on fuzzy observer was proposed in [11]. A Genetic based Fuzzy PID controller [12] has been proposed to synchronization task of chaotic systems in which one system has been considered as "master" whilst the other system has been treated as "slave" (a perturbed system with uncertainty and disturbance). In [13], two identical generalized Lorenz systems have been synchronized by a fuzzy controller based on mamdani approach and stability of the proposed scheme has been established by the Lyapunov stability theorem. In [14], the new 3 dimensional chaotic system was first investigated and then utilized an intelligent controller based on brain emotional learning (BELBIC), this new chaotic system was synchronized. In [15], stabilization and synchronization problem of the new hyperchaotic system was investigated. state dependent Riccati equation (SDRE) was applied to new hyperchaotic system in three ways. Stabilized system with know parameters, stabilized system with unknow parameters, sysnchronized system.

The rest of the paper is organized as follows. In Section 2, the T–S fuzzy models will be presented for a new 3D chaotic system. In Section 3, fuzzy stability of chaotic system is presented. In Section 4, synchronization between two new fuzzy chaotic system is achieved by generalized backstepping method is described. In Section 5, synchronization between two different fuzzy chaotic systems is achieved by active control. Finally, Section 6 provides, conclusion of this work.

• II.    T–S fuzzy model of new 3D chaotic system

The T–S fuzzy dynamic model originates from Takagi and Sugeno [16], which is described by fuzzy IF-THEN rules where the consequent parts represent local linear models. Consider a continuous-time nonlinear dynamic equation as follows:

x (t) = f(x(t)) + g(x(t))u(t)        (1)

Then the T–S fuzzy model is composed of the following rules:

Rule i: If z 1 (t) is M_t1 & — & z_p(t) is M_ip then x (t) = A_tx(t) + Bu(t), i = 1,2, —, r.                      (2)

Where Z 1 (t)~Z_p(t) are the premise variableswhich would consist of the states of the system, Мц (j = 1, 2, ..., p) are fuzzy sets, r is the number of fuzzy rules, A , , В are system matrices with appropriate dimensions. The final output of the fuzzy system is inferred as follows:

x (t) = Z [ ₌ i i_i(z(t))(A_/x(t) + Bu(t))      (3)

Where,

p hi(z(t)) = ЕГ^1^^)) , Wi(z(t)) = ПМ/7' ^(t))

^{1 1}              (4)

Lemma [17]. The equilibrium of the continuous fuzzy system (3) with u(t) = 0 is globally asymptotically stable if there exists a common positive definite matrix P such that

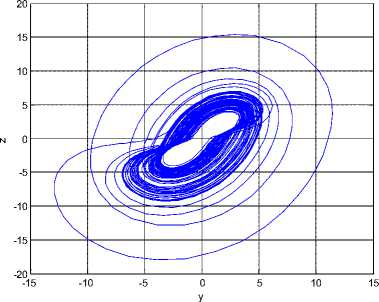
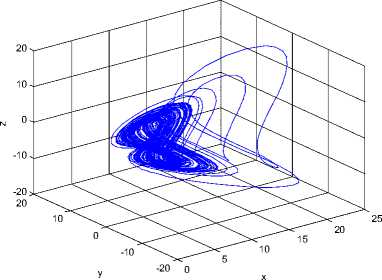
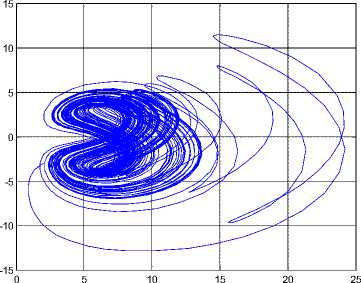
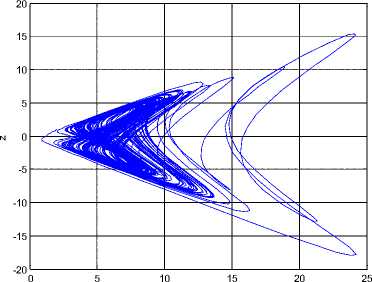
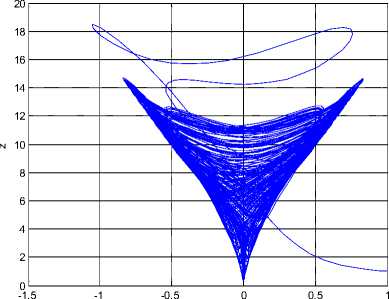
Fig 1. Strange attractors system (6)

A f P + PA , <0, i = 1,2, —, r           (5)

that is, a common P has to exist for all subsystems.

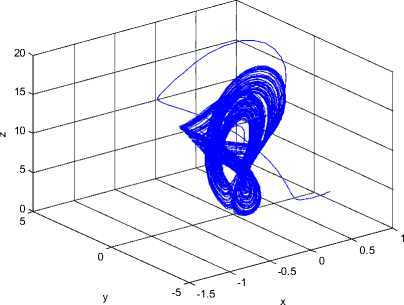
Recently, Sara Dadras and Hamid Reza Momeni constructed the 3D autonomous chaotic system [18]. The system is described by.

x = у - ax + byz у = су - xz + z             (6)

Z = dxy - hz

Where a, b, с, d, h are positive constants and x, y, z are variables of the system, when a = 3, b = 2.7, с = 4.7, d = 2, h = 9, the system (6) is chaotic. See Figure 1.

Assume that x £ [-g, g], у £ [-g, g] and g > 0, then system (6) can be exactly represented by T–S fuzzy model as following:

Rule 1: if x is M 1 & у is N 1 then X ( t) = A 1 X (t)

Rule 2: if x is M 1 & у is N₂ then X (t) = A₂X(t)

Rule 3: if x is M₂ & у is N 1 then X (t) = A₃X(t)

Rule 4: if x is M₂ & у is N₂ then X (t) = A₄X (t)     (7)

Here,

X = [x у z]^T

M, (x) = ¹ (1+ ^x ) ,M₂ (x) = ¹ (1 - ^x )

2 g           2 gj

^Ni№ = K^{1 +} ;И« = K¹ - f)   (8)

And states matrixes are:

Rule 1: if x is M 1 &  у is N 1 then X (t) = A 1 X(t) +

Bu(t)

Rule 2: if x is M 1 &  у is N₂ then X (t) = A₂X(t) +

Bu(t)

Rule 3: if x is M₂ &  у is N 1 then X (t) = A₃X(t) +

Bu(t)

Rule 4: if x is M₂ &  у is N₂ then X (t) = A₄X(t) +

Bu(t)                                               (11)

B -0

Where

According to the Generalized

Backstepping Method [19, 20] theorem, the control signal will be obtained:

Г -a  1     bg

A 1 = I 0 c 1 - gl 0   dg  -h

Г -a  1   -bg I

A₂ = I 0 c 1 -gl 0 dg -h [-a 1 bg 0     c    1 + g

0    -dg -h .

	—a	1	-bg"
A 4 =	0	c	1 + g	(9)
	. 0	-dg	-h .

That g = 30. So the final output of the fuzzy system (7) is inferred as follows and the chaotic behavior is shown in Figure 2.

X (t) = T. 4= ₁M_i(x)N_i(у)A_iX(t)        (10)

To support our analysis to be carried out in the following sections, some existing results are needed.

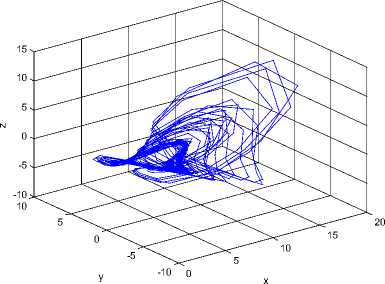
Fig 2. Chaotic behavior of fuzzy system (7).

• III.    Fuzzy stability of new chaotic system

For new chaotic fuzzy system (7), the following fuzzy controller is used to stabilize it.

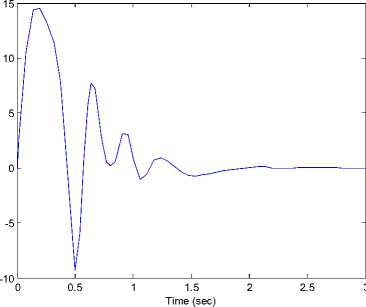
Figure 3 shows that (x, у, z) states of new fuzzy chaotic system (7) can be stabilized with the control laws u (12) to the origin point(0,0,0). The time response of the control input u for the stabilization new fuzzy chaotic system (7) shown in Figure 4.

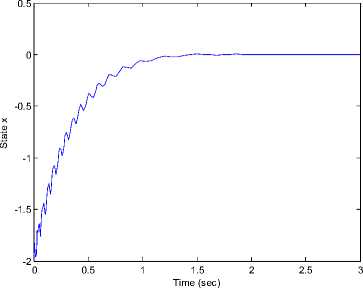
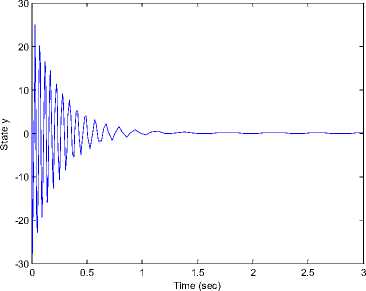
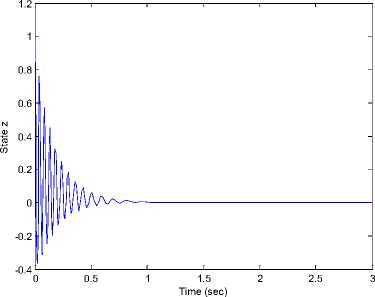
Fig 3. The time response of the states (x, y, z) for the controlled new fuzzy chaotic system (7) where the control inputs is (12).

^P =I

' 0.1429

—0.714

.61.9693

—0.714

0.2143

— 274.9887

61.9693 —274.9887 200466.879

I (16)

IV. Fuzzy Synchronization Of New Chaotic System

In order to achieve the behavior of the synchronization between two new fuzzy chaotic system by using the generalized backstepping metod, suppose the drive system (7) and the slave system takes the following from.

■ t

t

Rule 1: if x is M 1 & y is N 1 then X(t) = A 1 X(t) + Bu(t)

■ t

t

Rule 2: if 5c is M 1 & y is N 2 then X(t) = A 2 X(t) + Bu(t)

■ t

t

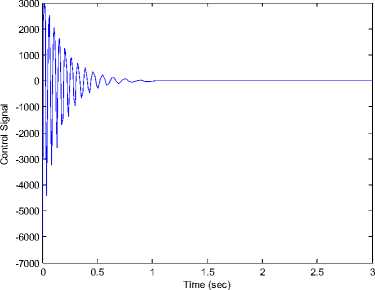
Fig 4. The time response of the control input .

Substituting equation (12) into equation (11) yields.

Rule 3: if 5c is M 2 & y is N 1 then X(t) = A₃X(t) + Bu(t)

■ t

t

Rule 4: if 5c is M 2 & y is N 2 then X(t) = A₄X(t) + Bu(t)

Where

X = [5c y Z]^T, u ⁽ t) = [u i ⁽0  u 2 ⁽ t ^{)] T},

B -E -I

Then the defuzzification process is given as

X(t) = T. i=i M_tUc)N (y) (A_tX (t) + Bu(t))

Rule 1: if 5 is M 1 &  y is N 1 then X (t) = A 1 X(t) Rule 2: if 5 is M 1 &  y is N 2 then X (t) = A 2 X(t) Rule 3: if 5 is M 2 &  y is N 1 then X (t) = A₃X(t) Rule 4: if 5 is M 2 &  y is N 2 then X (t) = A₄X(t)

Assume that e(t) = X(t) — X(t), we obtain

Where

e ⁽ t) =

1. 4=1 M_t(x)N i (y)A_tX(t) — X 4=i M_t(x)N i (y) (A ; X(t) +

Bu(t))                                           (20)

^A i

^A 2

^A 3

A 4

— d	1	bg
dbg — 1	—bg — 1	—dg — bg — ( bg)
0	dg	—h
— d	1	—bg
—dbg — 1	bg — 1	—dg + bg — ( bg)
0	dg	—h
— d	1	bg        "
dbg — 1	—bg — 1	dg — bg — ( bg)2
0	—dg	—h
— d	1	—bg     "
—dbg — 1	bg — 1	dg + bg — ( bg)2
0	—dg	—h

. 2

. 2

We select Q = I_3X3 and the matrix P will be obtained:

According to the Generalized Backstepping Method theorem, the control signals will be obtained:

Rule 1: if 5c is M₁ & y is N then [ ^u 1 ^(t) ] = u 2 (t)J

[ d — 2

I — ⁽ bg + 1)

^{— (c + 3) —(bg — g +} 1)1

—dg       h— 2    ^]e(t)

Rule 2: if 5c is M_T & y is N₂ then [ ^u 1 ^(t )] = u 2 (t)J

d ■

I bg

—

—

■ 1

—(c + 3) bg + g

—dg

h —

2 ^1]e(t)

Rule 3: if x is M₂ &  y is N then [ ^u 1 ^(t) l = 2        1        ^(t)

A{P + PA i = —Q, i = 1,2,3,4

Г d — 2

[— ⁽ bg + 1)

^{— (c + 3) —(bg + g +} 1)

dg        h— 2    ^]e(t)

Rule 4: if x is M₂ & у is N₂ then

Г u — 2

I bg — 1

—(c + 3) dg

bg — g — h — 2

[u i ⁽ t) L u₂ ⁽ t)

1] e(t)

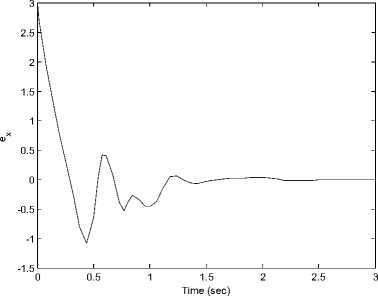
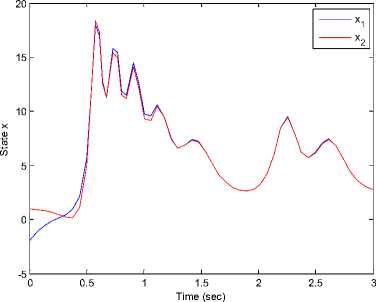
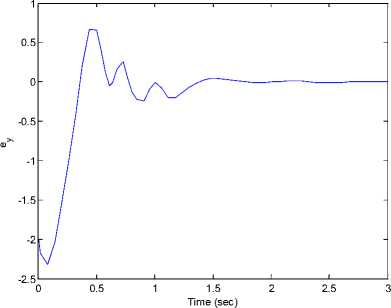
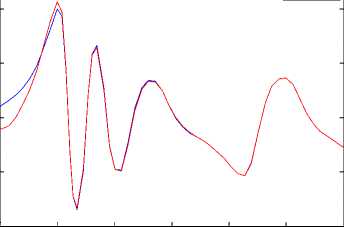
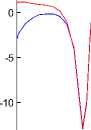
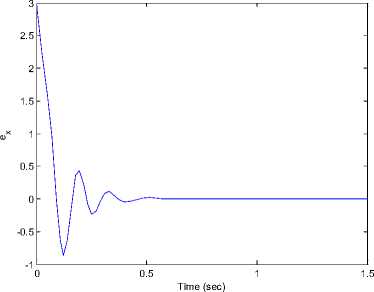
The initial values of the the drive and response systems are x 1 (0) = —2,у 1 (0) = 1,z 1 (0) = —3 and x₂(0) = 1, у₂(0) = — 1, z₂(0) = 1 respectively. The time response of x, у, z states for drive system (7) and the response system (17) shown in Figure 5. Synchronization errors (e_x, e_y, e_z) in the new fuzzy chaotic systems shown in Figure 6. The time response of the control inputs (u 1 , u₂) for the synchronization new fuzzy chaotic systems shown in Figure 7.

y1 y2

0          0.5          1           1.5          2          2.5          3

Time (sec)

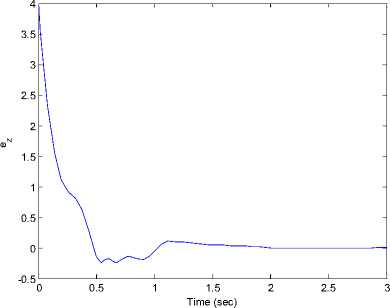
Fig 6. Synchronization errors (ex, ey, ez) in drive system (7) and response system (17).

-15

2         2.5

Time (sec)

Fig 5. The time response of signals (x, у, z) for drive system (7) and response system (17).

0         0.5

1           1.5          2

Time (sec)

Fig 7. The time response of the control inputs (U1, u₂) for drive system (7) and response system (17).

Substituting equation (21) into equation (17) yields.

Rule 1: If x is M 1 & у is N 1 then e(t) — A₁e(t')

Rule 2: if x is M 1 & у is N₂ then e(t) — A₂e(t)

Rule 3: if x is M₂ & у is N 1 then e (t) = A₃e(t)

Rule 4: if x is M₂ & у is N₂ then e(t) — A₄e(t) (22)

Where

^A 1 — ^A 3

^A 2 ^{— A} 4

—a 1 bg a — 2    —3 -bg

-(bg +1)  0   —2

—a 1 —bg a — 2  — 3 bg bg — 1  0   —2

We select Q — 7_3x3 and the matrix P will be obtained:

A T p + PA ; —		—Q ,	i —	1,2,3,4	(24)
	г 119	13	-5-|
	576	192	96
p —	21 192	109 576	- 96		(25)
	-5	-1	1
	- 96	96	4 ^

• V.    Fuzzy Synchronization Of Two Different Chaotic System

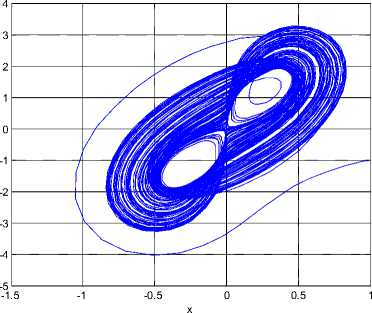
Recently, Chunlai Li, Hongmin Li and Yaonan Tong constructed the 3D autonomous chaotic system [21]. The system is described by.

x — —ax + byz у — су — fxz Z — йу² — hz

Where a, b, с, й, f, h are positive constants and x, у, z are variables of the system, when a — 16, b — 0.5, с — 10, й — 18, f — 6, h — 5, the system (26) is chaotic. See Figure 8.

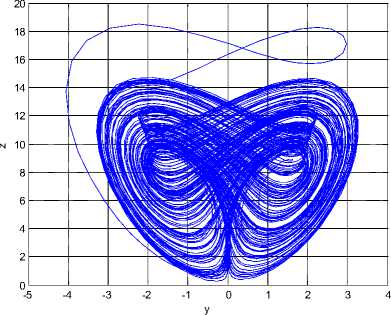
Fig 8. Strange attractors system (26)

Assume that x £ [—5,5], у £ [—5,5] and 5 > 0, then

system (26) can be exactly represente		d by T–S	fuzzy	Master Sуstem:
model as following: Rule 1: if x is Mi &  у Rule 2: if x is Mi &  у Rule 3: if x is M2 &  у Rule 4: if x is M2 &  у Here, X M i (x)=| (1 N 1 (у)= | (1 And states matrixes are A i = A 2 = A 3 = A 4 = That 5 = 30. So the (27) is inferred as fol shown in Figure 9.	is Ni then X (t) = is N2 then X (t) = is Ni then X (t) = is N2 then X (t) = [x у zf + x) ,M2(x)=| 5/           2 +;>« = ! ( —a  0    b5 0    c  —f5 0   d5  —h —a   0    —b5 0     c   —f5 0   —^5  —h —a 0 b5 0 c f5 0 d5 —h — a 0   —b £ 0     c    f5 0   —d5 —h final output of t lows and the cha	-- A i X(t) = A 2 X(t) - A 3 X(t) = A4X(t)    (27) (1—5) 1 Ч)    (28) (29) he fuzzy system otic behavior is			Rule 1: if x is Mi "—a i    0     b i 5 0     Ci   —fa 0    d 1 5  —hi Rule 2: if x is Mi —a i    О    —b 0      C i —f 0 —d i 5  — Rule 3: if x is M2 "—a i    0     b i 5" 0      C i    f i 5 0    di5  —hi Rule 4: if x is M2 —a i    О    —b 0       C i      f i 0 —d i 5  — And Slave Sуstem: Rule 1: if 5c is Mi " —a 2    1     b 2 5 0      C 2   1 — . 0 d 2 5 —h2 Rule 2: if 5c is Mi " —a 2    1     —b 2^ 0      C 2   1 — . 0 d25 —h2	& & i 5 i.9 h i & X & i 5 5 h i & 5 & 5 l	v is Ni then X(t) = X(t) v is N2 then X (t) = X(t) И is Ni then X (t) = (t) И is N2 then X (t) = X(t) c is Ni then X (t) = )t(t) + Bu(t) c is N2 then Xi (t) = X(t) + Bu(t)	(31)
X (t) = Z 4=i M/ (x)N; (у)A/X(t)           (30) To support our analysis to be carried out in the following sections, some existing results are needed.					Rule 3: if xc is M2 &  " —a 2     1      b 2 5 0      C 2    1 + 5 - 0    —d 2 5   —h 2		c is Ni then X (t) = X(t) + Bu(t)

Fig 9. Chaotic behavior of fuzzy system (27).

Suppose the master and slave systems takes the following from

I 0 C 2    1 + 5lX(t) + Bu(t)               (32)

^{0   —} ^ 2 ^{д —h} 2

Where

u(t) = [u^t) U 2 ⁽ t) U 3 ⁽ t)]^T

10 0

В = I0 1 0l                (33)

L 001

Assume that e(t) = X(t) — X(t), we obtain

e ⁽ t) =

Z 4=i M_/ (x)N_i(у)A_iX(t) — Z 4=1 M_t(x)N_t (у) (A_tX(t) +

Bu(t))                                           (34)

Rewrite the equation (34), we obtain

Rule 1: if x is M_i & у is N_i then e(t) = A_ie(t) +

A_iX(t) + Bu(t)

Rule 2: if x is M_i & у is N₂ then e (t) = A₂e(t) +

A₂X(t) + Bu(t)

Rule 3: if x is M₂ & у is N 1 then e(t) — A₃e(t) +

A₃X(t) + Bu(t)

Rule 3: if x is M₂ & у is N₁ then

" u i (t)" u 2 (t) , u 3 ( t )	— —	A 3 X(t) + B	" U i (t)" ^ 2 (t) , V 3 ( t).	&	" V i (t) V 2 (t) . v 3 ( t).	—
—a2	+ k i	1	b 2 9
—	0	C 2 + k 2	1 + 9   e(t)
	0	—d 2 9	— h 2 +	k 3

Rule 4: if x is M2 & у is N2		then e(t) = A4	e ( t) +
A4X(t) + Bu(t)			(35)
Where
г —U 2    1     b 2 9 1
A i = 1 0      C 2    1 — 9 1
L 0   ^ 2 9 —h 2 j
	ai — a2       1	( b 2 — b i )9
A i —	0         C 2 — C 1	f i 9 — 1 + 9
	0      ( ^ 2 — d i )9	h i — h 2  _
Г — ^ 2    1    —b 2 9]
A 2 — 1 0      C 2    1 — 9 1
L 0 d29 —h2 J
	ai — a2       1	( b i — b 2 )9
A 2 —	0         C 2 — C 1	f i 9 — 1 + 9
	0      (d i — ^ 2 )9     h i — h- 2
	—a 2     1      b 2 9 "
A 3 —	0      C 2    1 + 9
	0   —^ 2 9    —h2 -
	a i — a 2       1	( b 2 — b i )9
A 3 —	0         C 2 — C 1	1 + 9 — f i 9
	0     (d 2 — d i ) 9    h i — h 2
	—a 2    1     —b 2 9"
A 4 —	0      C 2    1 + 9
	0   —^ 2 9    —h2 -
	a i — a 2       1	( b i — b 2 )9"
A 4 =	0         C 2 — C i	1 + 9 — f i 9	(36)
	0      ( d i — d 2 )9	h i — h2  _

According to the Active Control Method, the control signals will be obtained:

Rule 4: if x is M2 &  у is N2 then

u i ( t)l                      r^ i ( t)l     pi ( t )

u 2 ( t) — —A 4 X(t) + B V 2 ( t) &  V 2 ( t) —

. u3 ( t)J                   Р3(0]    |т3(0

— a 2 + k i     1       —b 2 9

—     0       C 2 + k 2    1 + 9 e(t)

0       —d 2 9   —h 2 + k 3

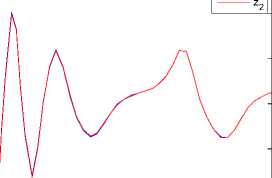
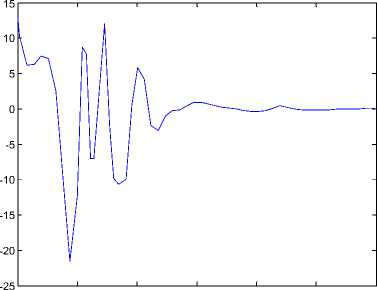
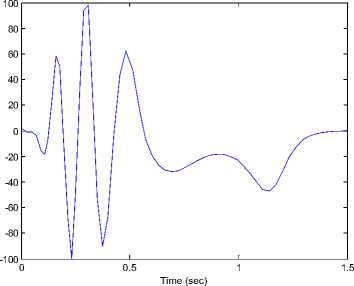
Where k [ , i — 1,2,3 are positive gains. We select the gains of controllers (37) k_i — 10, k₂ — 10, k₃ — 10. The initial values of the the drive and response systems are x_i(0) = 2.2, у₁(0) = 2.4, z_i(0) = 3 and x₂(0) = -2.2,у₂ (0) = -2.4, z₂ (0) = —3 respectively. The time response of x, у, z states for drive system (31) and the response system (32) shown in Figure 10. Synchronization errors ^e_x, e ^ , e_z) shown in Figure 11. The time response of the control inputs (u_i, u₂, u₃) for the synchronization two different fuzzy chaotic systems shown in Figure 12.

Rule 1: if x is M_i & у is N_i then

u i ⁽ t ⁾ u 2 ⁽ t) u₃ ⁽ t)

—A i X(t) + в

-Й 2 + ^k i 1

0 C 2 + ^ 2

0         ^ 2 9

U i ⁽ t ⁾ V 2 ⁽ t) . V3 ⁽ t)

b 2 9

^{1 —} 9

'V;U') V 2 ⁽ t) . V3 ⁽ t)

e ⁽ t)

^-h 2 ^{+ k} 3

Rule 2: if x is M_i & у is N₂ then

u i (t) u 2 (t) u 3 (t)	— —A 2 X ( t) + в		v i (t)" ^ 2 (t) . v3 ( t).	&		V i (t) ^ 2 ( t) . ^ 3 ( t)
[ —a 2	+ k i	1	—b 2 9
1	0	C 2 + k 2	1 — 9		e ( t)
	0	d 2 9    —	h 2 + k 3

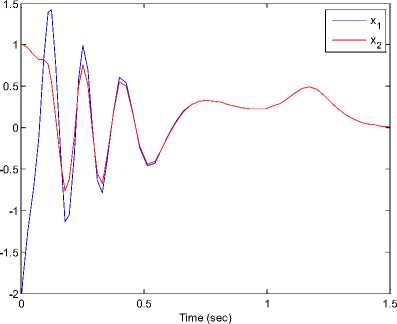
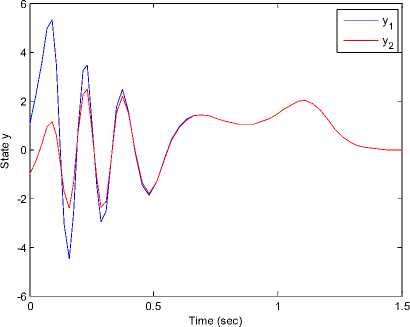
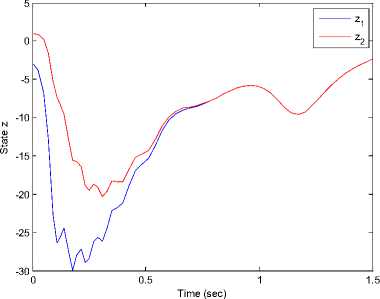
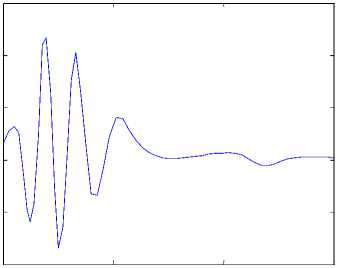
Fig 10. The time response of signals (%, y, z) for drive system (31) and response system (32).

-50

1.5

Time (sec)

-100

Time (sec)

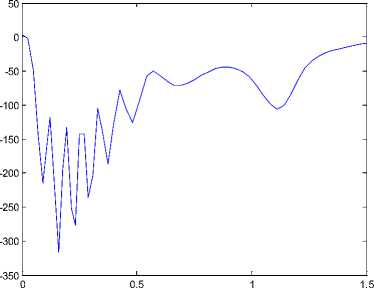
Fig 12. The time response of the control inputs (u 1 , u₂, u₃) for drive system (31) and response system (32).

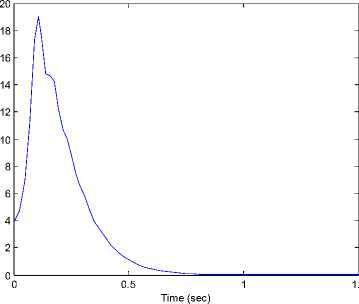
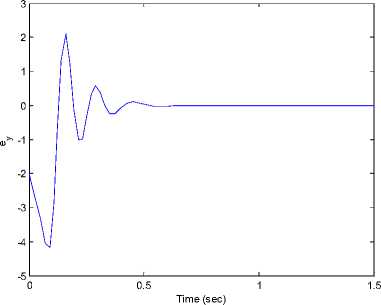
Fig 11. Synchronization errors (e_x, e_y, e₇^ in drive system (31) and response system (32).

Substituting equation (37) into equation (32) yields.

Rule 1: If 5c is M 1 & y is N 1 then e(t) = A 1 e(t)

Rule 2: if 5c is M 1 & y is N₂ then e (t) = A₂e(t)

Rule 3: if 5c is M₂ & y is N 1 then e (t) = A₃e(t)

Rule 4: if 5c is M₂ & y is N₂ then e(t) = A₄e(t) (38)

Where

г-ki0

A1 = A2 = A3 = A4 = I 0

^-k 3

I

We select Q = 7_3x3 and the matrix P will be obtained:

A?P + PA_t = -Q, i = 1,2,3,4        (40)

Р = 20 1 3X3                (41)

• VI.    Conclusion

In this paper, a fuzzy model-based designs for new 3D chaotic stability and synchronization have been proposed. Based on the fuzzy chaotic models, simpler fuzzy controllers have been designed for stabilizing and synchronizing new chaotic systems via generalized backstepping method. Then the synchronization of two different chaotic system are achieved by solving active control. Finally, numerical simulation was given to verify the effectiveness of the proposed controllers.