Galois field-based approach for rotation and scale invariant texture classification

A texture is a prime characteristic of surface properties of an object that distinguish it from other objects in an image. Texture analysis is very important in image processing and computer vision. It involves representing the characteristics of image regions in a form that can identify the type of image texture from a finite set of texture classes. Remote sensing analysis, medical image interpretation, pattern recognition and content-based image retrieval are some of the image-based applications, where texture analysis plays a fundamental and important role [1, 2].

Texture representations can be classified into five categories in terms of the feature types employed, namely, statistical [3], structural [4], geometrical [5], model based [6] and signal processing features [7]. The majority of existing texture analysis methods make assumption that texture images are acquired from the same viewpoint (i.e. the same scale and orientation). In image analysis applications, it is difficult to ensure that a captured texture image has the same viewpoint as the training images. Despite decades of research efforts, texture description remains a challenging problem, because of many variations that can affect texture patterns like rotation, scale, illumination and so on. Hence, invariant texture description is highly desirable from both theoretical and practical perspectives. Thus, many researchers address rotation and scale invariance issues in their work on texture analysis [8].

• II.    Related Work

Rotational invariance is achieved using a model based approach in [9] and signal processing approach in [5]. Other popular methods for rotation invariance texture classification include statistical approaches like Local Binary Patterns [10], wavelets [11], Gabor filters [12], Radon transform and Discrete Cosine Transform [13]. Recently rotation invariance has been obtained by a combination of extremum filtering, feature transform, scalar quantization and cross-scale joint coding for representing histograms in [14].

Scale invariance has been obtained by designing a histogram using Local Binary Pattern and fractal dimension image weights in [15]. Other scale invariant texture description methods include fractals [16], random projection [17], Harris and Laplacian key points [18] and

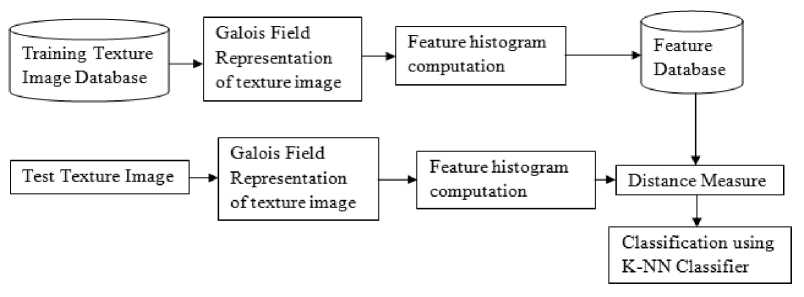
Fig.1. Flow design of the proposed method

pyramid histograms [19]. In [20], scale invariant classification of texture images in frequency domain has been achieved, whereas statistical approach is used in [21] and geometric approach is discussed in [19].

Despite its importance, work on simultaneous scale and rotation invariant texture representation is limited. The major existing approaches include psycho-physical transformation,      multi-resolution      simultaneous autoregressive (MRSAR) model [22], log-polar wavelet signatures [23], multichannel Gabor filtering [12, 24] and the Wold model [25] for invariant texture analysis.

Galois Fields has gained widespread applications in modern computer systems such as computer networks, satellite links or storage systems. These systems use finite field arithmetic for error correction or for cryptographic algorithms. Reed, Truong, Kwoh and Hall [26] proposed a Galois Field transform method for twodimensional filtering which is faster than the conventional Fast Fourier Transform algorithm.

In the present work, Galois Field-based approach in [27] is extended for rotation and scale invariant texture classification. Firstly, the Galois field operator is constructed, which is applied to the input textural image. The bin values of the normalized cumulative histogram constructed  for Galois Field operated image  are considered as texture features. These features  are inherently rotation and scale invariant due to the commutative and associative properties of Galois Field addition operator. These features are used for texture image classification using K-Nearest Neighbour classifier. The experimentation is performed on four benchmark texture datasets, namely, Brodatz, Mondial Marmi, Outex and Vectorial. The results are compared with that of Rotation Invariant Local Binary Pattern (RILBP) [10] and Log-Polar transform methods [23]. It is observed that Galois Field based approach achieves better classification accuracy when compared to other two methods.

The rest of the paper is organized as follows: The texture representation in Galois Field is described in Section III. In Section IV, the feature extraction and classification process is discussed. Experimental results and discussion is presented in Section V. Finally, Section VI gives conclusion.

• III.    Texture Representation in Galois Field (GF)

The flow design of the proposed method is shown in Fig. 1. Firstly, the Galois field operator is constructed, which is applied to the input textural image. A Galois Field (GF) is a finite field that contains a finite number of elements, called its order. Galois fields are given by the integers modulo a prime. i.e. for any prime integer p and any integer n greater than or equal to 1, there is a unique field with pn elements in it, denoted by GF(pn).

Consider a gray scale image I with intensity values in the range 0 to 255 which are represented in 8-bit binary form in the memory. Each pixel intensity value in its binary form can be considered as an element in a Finite Field of 2⁸, i.e., Galois Field GF(2⁸). We define a Galois Field operator as described below: Consider a 3 x 3 neighbourhood of a pixel I i,j in an image I. In GF(2⁸), perform mod 2 addition (denoted by ⊕ ) of eight neighbouring elements along with center pixel I i,j resulting in a 8-bit binary value I ′ i,j . The addition of all the nine elements in GF yields the same value irrespective of the order in which these elements are added. This GF operator is applied to all the pixels in the image I, which results in a transformed image I ′ .

For numerical illustration, consider the 3 x 3 neighbourhood of I i,j as shown in Fig. 2.

0111 1010	0110 0111	0101 1100
1010 0110	0111 1001	0101 1101
1101 0101	1010 0000	0110 1011

(a)

I i-1, j-1	I i-1,j	I i-1, j+1
I i, j-1	I i,j	I i,j+1
I i+1, j-1	I i+1, j	I i+1, j+1

(b)

Fig.2 (a). 8-bit binary form of 3 x 3 portion of an image I, (b). 8-nearest neighbourhood of I i,j

For example, the result Гц , that would be obtained when Galois Field operator is performed on 3 x 3 neighbourhood of I i,j Fig. 2(b), is computed as:

I'm = ((((((((I ij ® I i-1j ) ® W ) ® I i,j-1 ) ® WO ® I i+1, j ) ® I i+1, j+1 ) ® I i, j+1 ) ® I i-1,+1 )

The value obtained for portion of an image I shown in Fig. 2(a) is

I ’ ij = (1101 1101) 2 = (221) 10

d(p, q)

- J^(p‘—qj)

where pi, qi are the ith feature of test sample and training sample, respectively.

V. Experimental Results And Discussion

IV. A Feature Extraction

The histogram is constructed for the GF operated image. The histogram is represented as a discrete function

The experimentation is performed to evaluate the effectiveness of the proposed feature representation method in rotation and scale invariant texture classification.

A. Data Set

h(rk) = nk

The four benchmark texture datasets, namely, Brodatz [29], Mondial Marmi [30], Outex [31] and Vectorial [32] of planar images, which were considered by Bianconi and Fernandez [7], are used for experimentation.

where r k is the k^th value and n k is the number of r k values in the GF operated image.

The cumulative histogram is computed as

k

Ck= ^h(rj)

j=0

1) Brodatz

where k = 0, 1, 2, ..., 255.

The normalized cumulative histogram is given by

NCk =

Ck l|C||

The dataset has the following thirteen texture classes, namely, D112, D94, D92, D84, D68, D38, D29, D24, D19, D16, D15, D12 and D9. Each image is subdivided into 16 non-overlapping subimages that are of size 205 x 205 pixels. This results in 16 samples for each class. The dataset contains the images rotated in steps of 10 ° ranging from 0 ° to 90 ° [29]. The sample images of the texture class D84 for different rotation angles 0 ° to 90 ° in steps of 10 ° are shown in Fig. 3.

Where

||CH - Jc0 + c2 + .....+ cl + .... + c255

0 °

10 °

20 °

The bin values of the normalized cumulative histograms NC k are used for feature construction. The resultant features are considered as the rotation and scale invariant texture features.

B. Classification

The process of texture classification is to identify the type of unknown texture from a finite set of known texture classes. The classification approach comprises of two stages, namely, training and testing. The training stage consists of extracting the features from the training samples using the proposed method and is stored in the database for testing. The testing stage consists of extracting similar features from the test sample. The test sample is classified using the K-Nearest Neighbour classifier based on the similarity measure. The similarity between the test sample and the trained sample is measured by using the Euclidean distance metric [28] defined as:

30 °

40 °

50 °

60 °

70 °

80 °

90 °

Fig.3. Sample images of Brodatz D84 texture class with orientation angles 0o through 90o in steps of 10o.

2) Mondial Marmi

The dataset has twelve texture classes of granite tile images popularly used for color and texture analysis, namely, Rosa Porrio B, Rosa Porrio A, Rosa Beta, Giallo Veneziano, Criallo Santa Cecilia, Giallo Ornamentale, Giallo Napoletano, Bianco Sardo, Bianco Cristal, Azul Platino, Azul Capixaba, Acquamarina. The dataset has four images, each rotated by nine different angles (0 ° , 5 ° , 10 ° , 15 ° , 30 ° , 45 ° , 60 ° , 75 ° , 90 ° ) per class. Each image is subdivided into 4 non-overlapping subimages of size 272 x 272 [30]. The sample images of the texture class BiancoCristal_A for different rotation angles considered in the experimentations are shown in Fig. 4.

3) Outex

Outex is a widely used dataset for texture analysis. The images present in Outex_0045 are of 45 different classes. The original images are subdivided into 20 nonoverlapping subimages of resolutions 128 x 128. These images are rotated by nine different angles (0 ° , 5 ° , 10 ° , 15 ° , 30 ° , 45 ° , 60 ° , 75 ° , 90 ° ) [31]. The sample images of the texture class plastic001 for different rotation angles are shown in Fig. 5.

4) Vectorial

The Vectorial dataset contains 20 texture classes of artificial images. The texture classes are Abstract {1, 2, 3, 4}, circles{1, 2}, flowers{1, 2,  3}, leaves{1, 2}, squares{1, 2}, wallpaper{ 1, 2, 3, 4, 5, 6, 7}. The original images are subdivided into 4 x 4 non-overlapping samples of size 225 x 225 Each image is rotated by 10° ranging from 0° to 90° [32]. The sample images of the texture class Wallpaper_1 for different rotation angles are shown in Fig. 6.

0 °

5 °

10 °

20 °

15 °

60 °

30 °

75 °

45 °

90 °

0 °

10 °

50 °

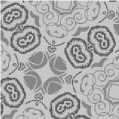
Fig.4. Sample images of Mondial Marmi BiancoCristal_A texture class with orientation angles 0o through 90o.

30 °

40 °

70 °

80 °

0 °                        5 °                        10 °

60 °

90 °

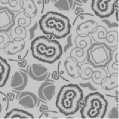
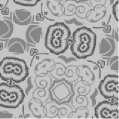
Fig.6. Sample images of Vectorial Wallpaper_1 texture class with orientation angles 0o through 90o in steps of 10o.

15 °                     30 °                     45 °

60 °                     75 °                     90 °

Fig.5. Sample images of Outex plastic001 texture class with orientation angles 0o through 90o.

B. Results and Discussion

Three different types of experimentation have been conducted, i.e. Rotation invariant, Scale invariant and Rotation-and-Scale invariant classification, to show the effectiveness of the proposed method.

1) Rotation invariant classification

In all the experiments for rotation invariance, the unrotated image (i.e. image at 0 ° ) is used as the training

sample and the images with different orientation angles are considered as the test samples. The experimental results are presented in Tables 1 and 2. Table 1 shows the classification results obtained using the proposed method and other state-of-the-art methods on Brodatz dataset. The feature vector consists of the normalized cumulative histogram bin values extracted from the Galois Field operated images. The texture image is rotated in steps of 10 ° upto 90 ° . Hence the number of orientations used for rotation invariant classification is 10. For the rotation invariant classification, a total of 208 x 10 images are used from the Brodatz dataset. The results obtained using the proposed method is compared with the original Local Binary Pattern method for rotation invariance (RI LBP) and Log-Polar transform method. The K-Nearest

Neighbour classifier is used for classification, where the values of K = 1, 3 and 5 are considered for the experimentation. As observed from Table 1, the Galois Field operator method classified the images with 93.17% accuracy as against the classification rate of 86.48% for RILBP and 91.25% for Log Polar transform method for K = 1. The classification results of the proposed method are also better when compared to other two methods for K = 3 and K = 5. The similar experiments are also performed on other three different datasets for K = 1. The average classification rate over all the angles on different datasets is shown in Table 2. From Tables 1 and 2, it is observed that Galois Field operator method outperforms RILBP and Log Polar transform method.

Table 1. Comparison of average classification rate over varying rotated angles on Brodatz dataset obtained using proposed method with RILBP and Log-Polar transform for K = 1, 3 and 5.

Testing Angles	RILBP [10](%)			Log-Polar Transform [23] (%)			GF operator (proposed method) (%)
	K = 1	K = 3	K = 5	K = 1	K = 3	K = 5	K = 1	K = 3	K = 5
0	100	98.56	97.60	100	93.75	89.42	100	92.31	88.46
10	87.98	87.50	83.66	89.42	85.58	80.77	91.83	92.31	88.94
20	80.77	80.77	79.81	93.75	87.50	82.70	95.67	93.75	91.35
30	82.69	81.25	80.77	90.87	88.94	86.53	95.19	92.31	90.39
40	83.17	83.65	82.22	91.35	86.06	83.65	91.35	91.35	87.02
50	82.21	81.25	79.33	89.90	85.10	82.69	89.90	87.50	87.50
60	73.56	72.12	74.52	87.02	85.10	82.69	88.46	87.50	86.06
70	80.29	79.81	79.81	89.42	89.91	83.17	91.83	92.79	87.98
80	87.02	86.06	84.62	90.87	85.58	82.69	94.71	90.87	88.94
90	97.12	96.16	97.12	89.90	88.46	82.69	92.79	92.79	90.38
Mean	85.48	84.71	83.94	91.25	87.60	83.71	93.17	91.35	88.71

Table 2. Average classifications rates (%) over all the angles on different datasets for K = 1 obtained by proposed GF operator, RILBP and Log-Polar transform methods.

Datasets	RI LBP [10](%)	Log-Polar Transform [23](%)	GF operator (proposed method)(%)
Brodatz	85.48	91.25	93.17
Mondial Marmi	84.73	90.74	93.11
Outex	77.74	75.99	80.05
Vectorial	74.41	96.34	96.25

Table 3. Classifications rate (%) over different scales 1.2 to 3.0 in steps of 0.2 on four different datasets obtained by the proposed method for K = 1.

Scale	Brodatz	Mondial Marmi	Outex	Vectorial
1.0	67.3077	63.0208	30.5556	91.5625
1.2	82.6923	73.4375	59.1111	95
1.4	89.9038	82.2917	75.8889	95.9375
1.6	91.3462	87.5000	86.2222	99.0625
1.8	97.5692	95.8333	96.3333	100
2.0	100	100	100	100
2.2	99.0385	96.3542	96.5556	100
2.4	95.1923	86.9792	87.1111	99.3750
2.6	93.7500	80.7392	80.4444	99.3750
2.8	90.3846	78.1250	75.2222	97.1875
3.0	88.4615	75.5208	69.4444	95
Average	90.5157	83.6174	77.8989	97.5

Table 4. Comparison of average classification rates (%) over all the scales considered on different datasets obtained by using proposed method with RILBP and Log-Polar transform for K = 1.

Datasets	RI LBP [10](%)	Log-Polar Transform [23](%)	GF operator (proposed method)(%)
Brodatz	39.2482	88.7674	90.5157
Mondial Marmi	33.6647	81.2481	83.6174
Outex	19.4949	77.2222	77.8989
Vectorial	54.5736	97.4715	97.5

Table 5. Classification rate (%) over all the orientation angles and scales on four different datasets for K = 1.

Datasets	RILBP [10](%)	Log-Polar Transform [23](%)	GF operator (proposed method)(%)
Brodatz	37.8702	79.7404	82.3846
Mondial Marmi	33.5938	74.1956	77.3611
Outex	16.4926	60.1617	63.2012
Vectorial	46.1125	90.0812	89.0563

• 2)    Scale invariant classification

For scale invariance, the texture images in the database are scaled by scaling factor of 1.0 to 3.0 with step 0.2. The sample images of texture classes of Brodatz, Mondial Marmi, Outex and Vectorial datasets for scales 1.2 to 3.0 in steps of 0.2 are shown in Fig 7, Fig 8, Fig 9 and Fig 10 respectively. The images of scale factor 2.0 are used as the training samples and the remaining images of different scales are used as testing samples. The Galois Field operator method is applied on each scaled image. For scale invariant classification, 208 x 10 images from the Brodatz dataset, 192 x 10 images from Mondial Marmi, 900 x 10 images from Outex and 320 x 10 images from Vectorial dataset are considered. Table 3 shows the classification rates obtained by proposed method over the different scales for the four different datasets. The comparison of average percentage of classification over all the scales on four different datasets obtained by using the proposed method over RILBP and Log-Polar transform is presented in Table 4. From the Table 4, it is seen that the proposed method outperforms the other two methods.

• 3)    Rotation-and-Scale invariant classification

For the experimentation, the datasets are created by first rotating the images and then scaling the rotated images to different sizes. The images are cropped from the center to maintain the original size of the image. The unrotated (at 0o) and scaled images with scale factor 2 are chosen as the training samples and the remaining rotated and scaled images are the testing samples for the evaluation of performance of the proposed method. Table 5 shows the classification performance obtained by the proposed method on rotated and scaled images for four different datasets. From Table 5, it is observed that the proposed method has better classification rates when compared to other two methods.

Over all, it is also observed that, only in case of Vectorial dataset, the performance of proposed GF operator is comparable to Log-Polar transform. In case of other three datasets, proposed GF operator outperforms RILBP and Log-Polar transform.

М№Ю

• 1.2                      1.41.6

Ж HI IK

• 1.8                     2.02.2

• 2.4                    2.62.8

• 3.0

IK III III

III

Fig.7. Sample images of Brodatz D15 texture class for all scale factors

1.2 to 3.0 in steps of 0.2

Fig.8. Sample images of Mondial Marmi GialloNapoletano_A_1 texture class for all scale factors 1.2 to 3.0 in steps of 0.2

1.2                      1.4                      1.6

1.8                    2.0                    2.2

2.4                    2.6                    2.8

3.0

3.0

1.6

1.2

1.4

2.0

2.6

2.2

1.8

1.4

2.8

2.4

3.0

2.0

2.6

2.8

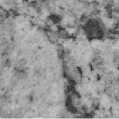
Fig.9. Sample images of Outex plastic038 texture class for all scale factors 1.2 to 3.0 in steps of 0.2

Fig.10. Sample images of Vectorial Flowers_1 texture class for all scale factors 1.2 to 3.0 in steps of 0.2

• VI. Conclusion

In this paper, a novel approach using Galois Field addition operator is proposed for rotation and scale invariant texture classification. The commutative and associative properties of Galois Field addition are helpful in achieving the rotation and scale invariance of texture classification. The effectiveness of the proposed GF approach has been demonstrated experimentally using four benchmark texture datasets, namely, Brodatz [29], Mondial Marmi [30], Outex [31] and Vectorial [32] of planar images. The results obtained by using the proposed GF approach are compared with that of RILBP and LogPolar transform methods. It is observed that the proposed GF approach is more effective as compared to other two methods in achieving rotation and scale invariance.