Galua Field Multipliers Core Generator

age. One of the possible methods is a method based on the use of EC isogenies in the Galois field GF(2^m). To calculate it, the same operations are used as in existing digital signature algorithms that use Galois fields GF(2^m). Also with the binary fields GF(2^m) other extended Galois fields GF(dⁿ) can be used, such that 2^m ≈ dⁿ. When processing codes of the elements of extended binary Galois fields, it is necessary to process binary codes, the length of which is m (according to modern standards, m can reach 1000). Processing of such codes is the purpose of operational units for Galois fields that are used in the IS based on EC. The article describes the tool for generating Galois field multipliers VHDL descriptions of different characteristic and different order, which are used in IS based on EC. A feature of IS algorithms is their multilevel structure, where specific mathematical operations on multi-bit codes are performed at different levels: operations over elements of prime GF(d) and extended GF(d^m) Galois fields, operations over points of elliptic curves. Depending on the conditions of use, it is necessary to provide the configuration of operating devices that implement these algorithms: to change the Galois field, the characteristic for the representation of field elements, to change the elliptic curve. One of the main elements for dedicated computers functional units design is FPGA, which has the following important features [2]:

• •    FPGA facilitates the next rapid transition to ASIC, that ensures mass production.

• •    FPGA provides hardware implementation of algorithms and storage within the chip of intermediate results in the execution of these algorithms.

• •    Modern FPGAs ensure the preservation of intellectual property and complicate unauthorized duplication and "reverse engineering".

• 2.    Related Work

• 3.    Problem Description

At the present stage, when ISs are implemented in the CFS, it becomes important to ensure their work in real-time. This requires the use of high-speed hardware solutions - dedicated processors, which are implemented in FPGA. The multi-level dedicated processor (SP), which performs operations over elliptic curve points when processing digital signatures, is used as a basis for designing IS tools. The design of such dedicated processor requires the use of special sections of mathematics: Galois fields, elliptic curves (EC), etc. Elements of Galois fields and EC points are represented by multi-bit binary codes (which are represented by hundreds and thousands of bits). SP requires original functional units to perform operations on them. The SP operates on the basis of such theoretical provisions that allow to consider it as a dedicated computer system with architecture that is different from the known architectures of usual computers. Modern computer tools are required to adhere to the principles of open systems, focusing on the use of open standards. Creating SP multiplier is one of the most difficult tasks. In this article, we will consider the creation of a Galois field multiplier core generator for SP.

Modern information security tools use operations on extended Galois fields GF(2ⁿ) with large degrees n, their elements are represented in the polynomial or normal basis [3]. That’s why the creation of tools for operations on the elements of such Galois fields is a very promising scientific and engineering direction. The investigation of the hardware, structural and time complexity of the multipliers of the elements of such fields is a difficult task, because you have to multiply the codes, the bit size of which coincides with the degree of the Galois field and can reach 1000 bits. The object of study are fields with characteristics that are prime numbers (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, …, 997). The order of such fields is approximately 2⁹⁹⁸.

In recent years, the concept of elliptical curves has found its application in cryptography [4]. The reason for this is that elliptic curves over finite fields form finite groups, on which it is easy to determine arithmetic operations due to the rich structure of the groups [5]. Until now, cryptography has worked with multiplicative groups on some finite fields. Elliptic curves are similar to these groups, but their advantage is that there is more freedom to choose an elliptic curve than to choose a finite field. In addition, elliptical cryptosystems provide better data protection. Galois field arithmetic is used to perform operations over points of elliptic curves, the element codes of such fields, are presented in polynomial or normal bases ([6, [7]) . Multipliers for Galois fields are characterized by high hardware [8], structural [9] and time [10] complexity.

In [11] architecture that trades a reduction in resources with an increase in the number of clock cycles is described. This architecture is also fine grain scalable in both the time and the area (or logic) dimensions thus facilitating implementations that maximize their use of finite FPGA resources while achieving fast computational speed. In [12] authors propose Galois field arithmetic using irreducible polynomial to generate the S-box for AES. In [13] authors consider a reconfigurable digital circuit which performs various Galois field arithmetic operations with the same set of hardware. Using this hardware, we can perform a few operations in parallel. In [14] authors show that the Reed-Solomon codes built on a Galois field of characteristic 3, can be used in transmission through a visible light communication channel, due to the information can be encoded using the colors red, green and blue. In [15] authors introduce the concept of multivalued neural element over Galois field relative to any system of characters of group on which we define logical functions. In [16] a method is proposed to implement Markov probability functions defined based on a stochastic matrix of a predefined size, when using a set of multivariate polynomials over Galois field and an array of evenly distributed non-correlated (pseudo) random numbers of a predefined capacity. In [17] new structure of square operator takes advantage of Normal Basis representation of GF elements is described. In [18] Galois fields are used to improve Energy Management System. In [19] authors demonstrate that Correlation Power Analysis using only a specific bit has the superior performance because of modulo operation in Galois field for AES-128 encryption algorithm use. The paper [20] considers algorithms for multiplying field elements, while paying attention to both table multiplication and multiplication "on the fly" and algorithms for calculating multiplicative inversion [21]. The research work [22] proposes a framework for checking the correctness of Galois field arithmetic operations in digital circuits. In [23] a technique is proposed for performing distributed nonlinear-polynomial (NP) computing over Galois field.

Many devices for processing Galois field GF(d^m) elements are known, which are used in various cryptographic transformations [24].

A matrix multiplier for binary numbers [25] which consists of Guild cells [26] is known. Also multiplier which is based on modified Guild cells to perform multiplication over Galois field elements GF(d^m) is known. In article [27] we are considered the hardware costs of matrix Galois field GF(d^m) multipliers when d < 4, in work [8] we are considered the hardware costs of multipliers when d ≤ 998. The process of creating core generators is described in [28].

For use extended Galois fields GF(dm) with characteristics d > 2 in data protection systems, it is necessary to choose a criterion for determining the best field. Also, using the proposed criterion, it is necessary to determine the best fields that should be used for data protection.

The internal structure of the modified Guild cells and its influence on the assessment of Galois field GF(d^m) multipliers hardware complexity is the subject of this work. The use of characteristic d > 2 is insufficiently researched and creates many more options for coding and, accordingly, can increase the resistance of the cipher to hacking [29].

Although there are many tools for creating Galois field multipliers on FPGA (field programming gate array) on hardware description languages (VHDL, Verilog, HLS), however, this approach is extremely time consuming. Therefore, there was a need to create a VHDL description generator of such multipliers. Described in this article generator allows the user to generate multipliers for FPGA, so user can explore their advantages and disadvantages.

• 4.    The Goal of the Work

The purpose of the work is to theoretically justify the feasibility of using extended Galois fields GF(dm) with characteristics d > 2 in data protection tools, to define a criterion for comparing data protection tools based on such Galois fields, to determine the best fields according to the chosen criterion. Also, the purpose of the article is to create a tool for generating VHDL descriptions of multipliers of elements of such fields for further use of these descriptions in the implementation of data protection tools on FPGAs.

The generator has to create multipliers according to the three most common variants:

• •    in base of Modified Guild Сell (MGC) which is presented as one whole element (a black box) – first variant.

• •     in base of MGC which is presented as multiplier and adder - second variant.

• •     in base of MGC which is a circuit that consists of simple logic gates and implements the result of Boolean

• 5.    Theoretical Background of Calculating the Hardware Costs of Multipliers

functions - third variant.

It is proposed to take the hardware complexity of the multipliers as a basis for comparing different extended Galois fields. It is also suggested to use multipliers based on Modified Guild Cells (MGC).

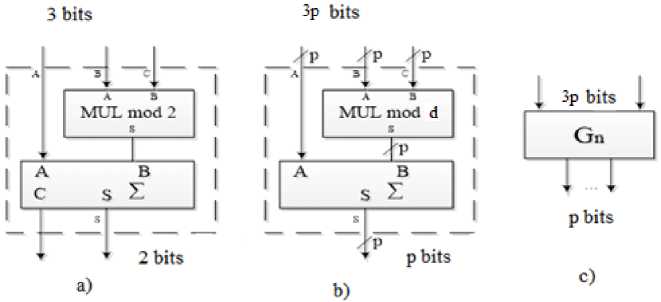
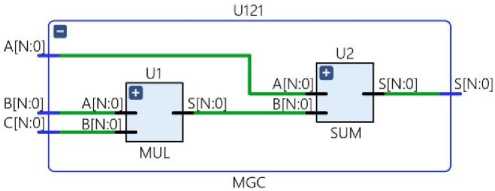
Fig.1. a) Guild Cell, b) scheme of the Modified Guild Cell for processing elements of Galois fields GF(dm), c) symbol of the Modified Guild Cell GF(dm)

The multiplier for Galois fields GF(d^m) can be implemented on the basis of Modified Guild Cells (MGC). MGCs for Galois fields GF(d^m) should have 3p inputs and p outputs, each p = [log₂ m] bit (Fig. 1). When using modern FPGAs, the logic cells of which are built on the basis of software 6-input combinational circuits (LUTs), the implementation of such Guild cells on the FPGA in the most general case, when the structure of the MCG is not specified, but only the number of its inputs and outputs is taken into account, requires q 1 = (2^3p-h-1 — 1) • p LUTs, h is the number of inputs of the LUT used. We use 6-input LUTs.

It is convenient to estimate the hardware complexity in comparison with the costs of the multiplier for the binary Galois Field GF(2n).

For the variant, when the MGC is a whole element, the coefficient of hardware complexity k_mul = k g * k_k , де

k_g = ^ ^gd^ , k^k  ^^ are coefficients of complexity of MGC, k g _d and k_g2 , k_kd and k_k2 are number of LUTs in

MGC and number of MGC for Galois Fields GF(dm) and GF(2n), respectively.

For binary Galois fields GF(2ⁿ) k_g2 = 1, for others k_gd = (2 P ^-h-1 — 1) * k, where p = 3 * [log₂ d], and k =[log₂ d]. It follows that k_gd = (2³ * ^riog 2 ^d]- ^ ^-1 — 1) * riog₂ d]. So:

kgd = (23*fiog2 d]-d-1 — 1) * [10g2 d],d > 3

In binary fields GF(2ⁿ) it is required to implement the multiplier with k_k2=2n² — 2n + 1 MGCs. In the Galois Field with a characteristic d GF(d^m) - k_kd = 2m² — 2m + 1 and additionally (m — 1) * (2³ * ^riog 2 ^d]-d-1 — 1) * [1og₂ d] LUTs needed to find the coefficient by which an irreducible polynomial must be multiplied. These hardware costs for the implementation of the element f, which forms this coefficient, can be neglected in this case, since they are small compared to the costs for the implementation of the MGCs themselves. The element f, used to find the coefficient by which to multiply the polynomial to sum the intermediate result, calculates a function that depends on two parameters: / = (d — G_m) mod d = (—G_m) mod d, where d is the basis of the field, G_m is the output of the Modified Guild Cell in the direct course of calculations. The coefficient at the highest degree of an irreducible polynomial is always equal to 1. So:

2m 2 -2m+1 2” 2 -2”+1

k k - the ratio of the number of MGC of the GF(d^m) field to GF(2ⁿ).

mul

⁽² 3*[^log2d^] h ^{1 —1)} *[l ^o g 2 ^d](2m 2 ^—2m+1) ~ ₂3*nog₂ dH-1   > з

2n 2 -2n+1                             '  ^_

k mul - the ratio of the number of LUTs of the GF(d^m) field to GF(2ⁿ).

2И2

In this case  dm ~ 2”  . Then m ® logd 2” = —— ,  kk ® (10fl2 d)7——^— ® log-1 d , kmui ® d       log, d ’    k       2n2-2n+1           2      ’

(23*flog2d1-h-l-1)(log2d) ~ 23*[log, dH-1. log, d

For small n k mul is necessary to calculate using more accurate formulas (1, 2, 3).

For the variant, when the MGC consists of a multiplier and an adder, each of which has 2p inputs and p outputs, evaluated separately, for the implementation of one MGC it will be necessary q₂ = 2 • (2^2p-d-1 — 1) • p LUTs.

q      (2 3?—h—1 —         23^—h—1

Then: — = ———r—----~ ——t— = 2^P-1 - the cost ratio for the implementation of one MGC according to the first q₂    2.(2 2P^-h-1 -1).p    2.2 2P^-h—1

and second variant. From the formula, we can see that the internal structure of the MGC significantly affects the estimation of hardware costs. Additional consideration of the internal structure of the MGC reduces the estimated value of hardware complexity compared to the first variant of estimating hardware costs, when only the number of inputs and outputs is considered.

Let's estimate hardware costs according to the second variant. For binary Galois fields k g ₂ = 1/2, for other fields k_gd = (2² *fl ^og 2 ^d]-d-1 — 1) * [1og₂ d] * 2. So:

kgd = |22*rlog2d]-^-1 — 1| * [iog2d] * 2

In binary fields GF(2n) it is required 2n2

GF(dm) - 2m2 — 2m + 1 MGC. So:

— 2n + 1 MGC to implement the multiplier, and in the Galois field

k

k

2m 2 -2m+1 2” 2 -2”+1

At the same time d^m ~ 2 ” . Then m ~ lo g _d 2 ”

2И² ___ 2П

”   7,  ~ Wos2 Ф Z°S2 d ,

, ^k   ^^

log 2 d ^K        2n 2 -2n+1

log-1 d,

..gd .'     *_ROg 2 d1 _ 4

^kmul       log₂ d       ²⁴

Comparing the formulas for finding kmul for the first and second cases, we see that in the second variant of the analysis of the hardware complexity of the MGC, at large values of p, the value of the hardware complexity generally decreases in 2p-1 times.

Now let's calculate the hardware costs for multipliers MGC that consist of small logical elements. SMn is a multiplier element that performs modular multiplication and addition and has result and carry outputs, i.e. it is a MGC. SMch is an element that performs the operation of adding or subtracting a number in the complementary code during division without restoring the remainders. Sn is a node that defines the type of operation, subtraction or addition when dividing without restoring remainders. Rn is an element that determines whether one more addition operation is required to find the result. Look Fig. 2.

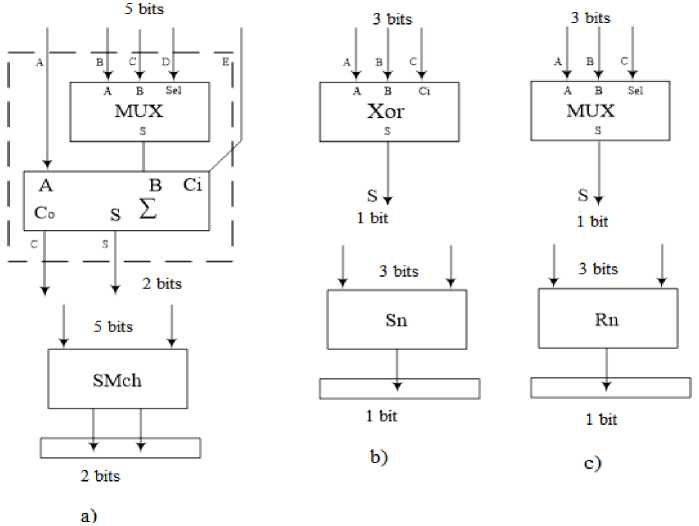
Fig.2. a) scheme and symbol of element SMch, b) scheme and symbol of element Sn, c) scheme and symbol of element Rn

The coefficient of hardware costs of the multiplier for the elements of the field GF(d^m) relative to the similar costs of the multiplier for the elements of the field GF(2ⁿ) k_mul = k_g * k_k , where k_g = ^^j^ , k^k ~^- coefficients of complexity and number of MGC, k g _d and ^k g2 , ^kkd and k_k2 are the number of LUTs in the MGC and the number of MGCs for the Galois fields GF(d^m) and GF(2ⁿ), respectively.

For binary Galuis Fields GF(2ⁿ) k g ₂ = 1, for another fields:

kgd= KSMn *KLUT1 + KSMch *KLUT2 + KSn *KLUT3 + KRn *KLUT4 + KSUMn *KLUT5,

KSMn, KSMch, KSn, KRn - number of elements, respectively, SMn, SMch, Sn, Rn in the Galois field multiplier, KSUMn – number of sumator elements, KLUTn - number of LUTs that are used for according element.

KLUT1 = KLUT2 = KLUT3 = KLUT4 = 1, KLUT5 = 2.

kgd= (flog2 d1)2 *2 + (flog2 d1)2 *2 + flog2 d1 * 1 + flogz d1 * 1 + [log2 d1 * 2

kgd = 2([log2 d1)2 + 2([log2 d1)2 + 2flog2 d1 + 2[log2 d1 = 4(flog2 dD2 + 4[log2 d1.

Then:

kg= 2([log2 d])2 + 2([log2d])2 + 1 [log2 d] + 2flog2 dl = 4(Tlog2 d])2 + 4flog2 d]               (7)

In binary fields GF(2ⁿ) to implement the multiplier it is required k_k2=2n ² — 2n + 1 Guild Cells, and in Galuis Fields GF(d^m) with the characteristic d k_kd=2m² — 2m + 1. Also, it is additionally necessary to have

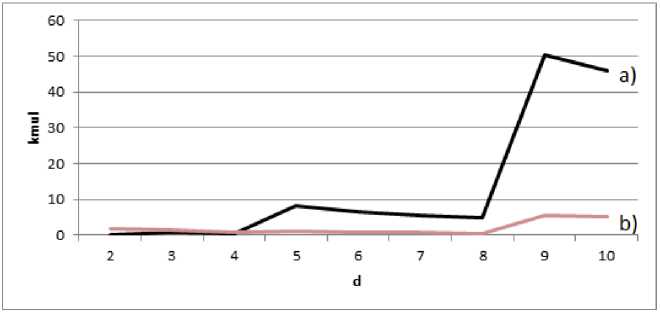
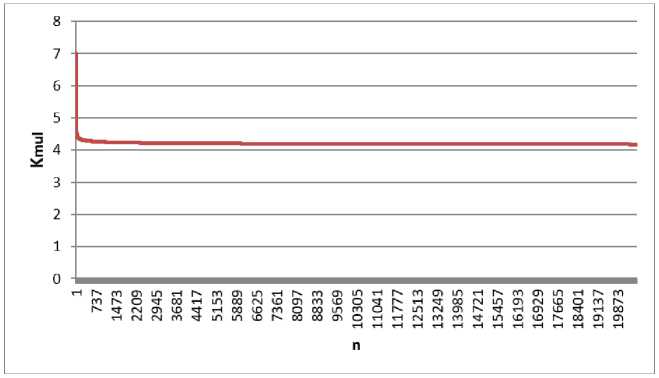
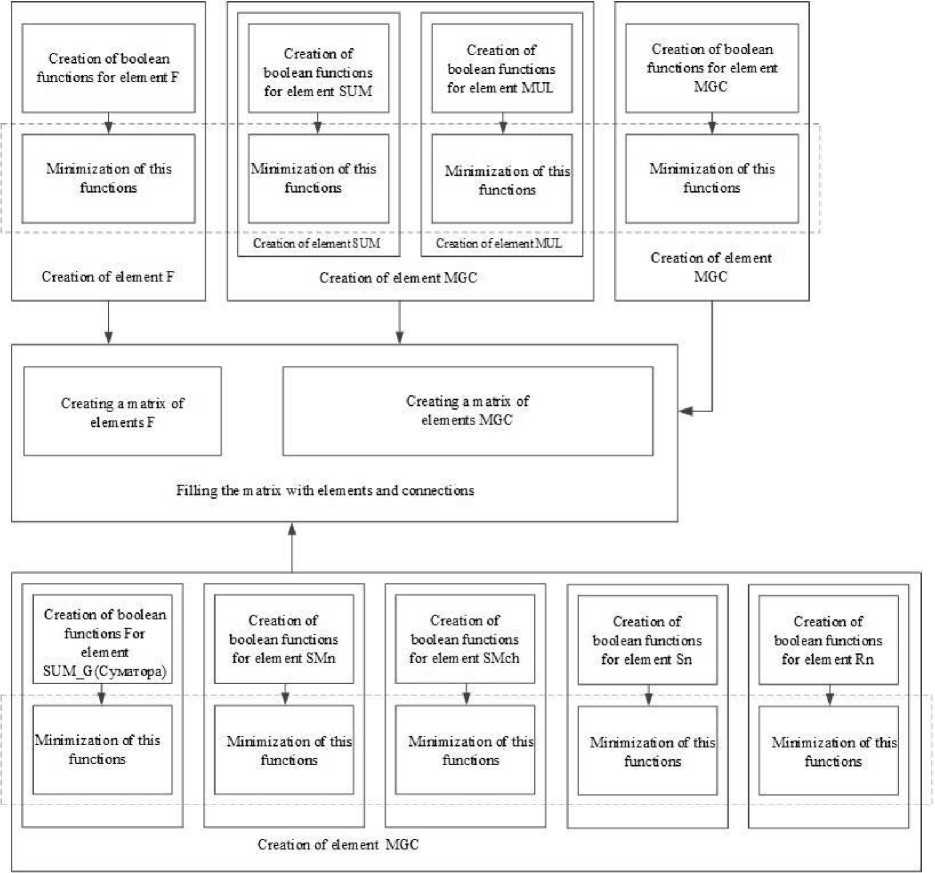
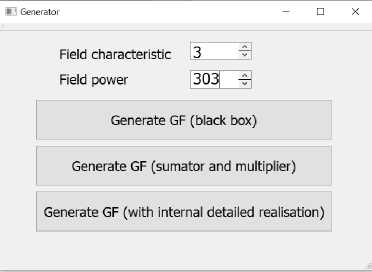
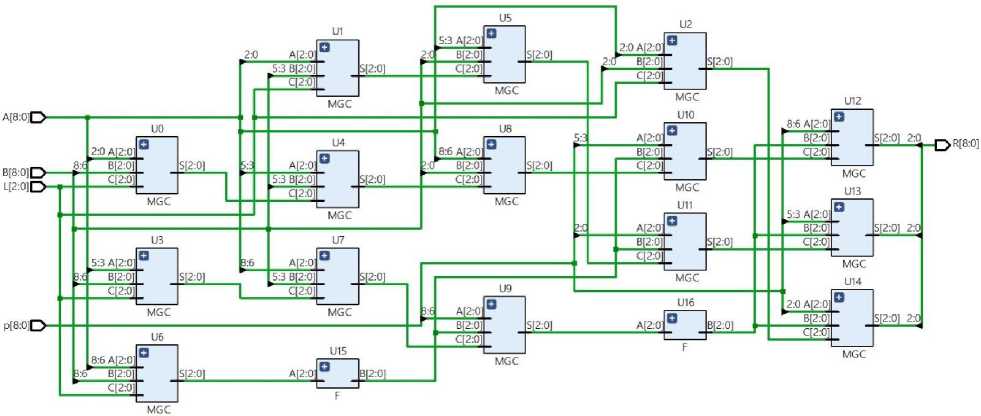
(m — 1) * (23

LUTs to find the coefficient by which the irreducible polynomial must be multiplied (these hardware factors can be neglected in this case, since they are small compared to the costs for the implementation of the Guild cells themselves). So:

^kmul

2m2-2m+1 k ®--;----- к   2П2-2П+1

(m)2

for big n

(4([log2 d^])²+4[log₂ d^])m² n²

,d> 2

and d^m ~ 2". Then m~log₄ 2"

;^, ^k_k « ^log-² d, ^k_mui

4([iog2 d^])²+4[tog2 d^]

(log₂ d)2      . ^llmd^^ ^kmui = ^4.

From Fig. 3 we can see that the better fields for first variant are with characteristic d = 3, for second variant – it’s are with characteristics d = 3, 5 and 7. For third variant fields with large characteristics have 4-time bigger hardware complexity than binary (Fig. 4).

Fig.3. The ratio of hardware costs of multipliers of elements of Galois fields GF(dm) and GF(2n) according to the first – a) and second – b) variant

Fig.4. The ratio of hardware costs of multipliers of elements of Galois fields GF(dm) and GF(2n) according to the third variant

• 6.    General Approach to the Design of Core Generators

VHDL [30] was chosen to develop kernel software models. Currently, there are many tools on the market for the development of integrated circuits on FPGA. However, they all have a significant drawback - design time. Therefore, project generation systems according to certain configuration parameters are becoming more and more relevant.

The multiplier is created from basic model device that can be configured by different parameters. Another approach to reducing design time is based on the use of high-level programming languages to describe hardware. Using this approach simplifies the design process and elevates it to the level of software design. This approach allows you to get both hardware and software to implement the task.

Significant disadvantages of modern design approaches are the use of specific high-level programming languages. This approach greatly complicates the design time and is based on the use of ready-made units, which greatly increases the number of resources used on the chip and increases the execution time of the program.

For many years, the efforts of VLSI developers [31] have been aimed at solving the problems of functional design at the level of register transfers [32]. Accordingly, the main investments were directed to the development of synthesis, modeling and verification tools at the RTL level. However, in recent years, VLSI and CAD developers have begun to pay attention to the system level of design. It's necessary due to the increase in the size of projects and the desire to reduce design costs. The main purpose of creating design tools at the system level is to simplify the design process, which assumes that the developer does not need to have perfect circuit design skills, but only be able to program in a high-level language.

Design tools must include the following requirements:

• •    ease of use. That is the friendliness of the interface and extensive functionality.

• •    ability to test the developed device.

• •    ability to estimate hardware costs, power consumption and performance of the synthesizied in FPGA device.

• •    ability to choose the best option. That is, the best one in terms of hardware costs, speed and power

consumption.

Modern development systems have the following problems:

• •    the complexity of the design process. The developer is required to have a deep knowledge of the hardware on which the device will be implemented.

• •    design time.

• •    performance of the developed device.

• 7.    Features of the Galois Fields Elements Multipliers Core Generators Design

To simplify and reduce design costs, ready-made circuit solutions are used. They are commonly called cores. In this approach, the device is designed on the basis of a ready-made and tested core. The core can be either the simple element of the processor or the entire processor. To ensure high performance in this approach, it is necessary that the structure of the core corresponds as accurately as possible to the task.

The core design process can be divided into two areas: creating a reconfigured unit and creating a configured one.

A reconfigured unit is an approach based on the use of a ready-made solution, with the ability to configure for a specific task, changing the values of certain parameters. Configured units are units that are created by a set of specific rules and algorithms, but they are created for a specific task.

There is a serious problem with creating Galois field elements multipliers - they are very large, but contain many similar units.

Next, you can consider comparing fields with the approximately equal orders but with different characteristics (Table 1). It is extremely difficult or almost impossible to manually create such multipliers. Therefore, it was decided to develop a Galois field multiplier generator for Galois fields with order approximately up to 2998 and with different characteristics.

The generator was implemented in C++. A block diagram of the generator is shown in Fig. 5. The generator implements multipliers by three variants:

• •    in base of Modified Guild Сell (MGC) which is presented as one whole element (a black box),

• •    in base of MGC which is presented as multiplier and adder,

• •    in base of MGC which is a circuit that consists of simple logic gates and implements the result of Boolean

functions minimization.

Table 1. The number of modified guild cells in Galois field multipliers with approximately equal order and different characteristics

The Galois field GF(dm) for which the FPGA multiplier is built	Galois field order (approximately, Od)	Relative Galois field order, ROd=Od/O2	Number of MGC (approximately, NC= m2 + (m-1)2	Number of MGC inputs and outputs (approximately, NI0 = Nr x 4x [log7 d])
GF(2998)	2,68e+300	1,00	1990013	7960052
GF(3630)	3,86e+300	1,44	792541	6340328
GF(5430)	3,60e+300	1,34	368941	4427292
GF(7355)	1,02e+300	0,38	251341	3016092
GF(11289)	9,17e+300	3,42	166465	2663440
GF(13270)	5,82e+300	2,17	145261	2324176
GF(17244)	1.69e+300	0,63	118585	2371700
GF(19235)	3,21e+300	1,19	109981	2199620
GF(23221)	8,74e+300	3,27	97241	1944820
GF(31201)	5,80e+299	0,22	80401	1608020
GF(37191)	3,36e+299	0,13	72581	1741944
GF(41186)	9,50e+299	0,35	68821	1651704
GF(43184)	3,61e+300	1,35	67345	1616280
GF(47180)	9,49e+300	3,54	64441	1546584
GF(53174)	1,06e+300	0,40	60205	1444920

Fig.5. Block diagram of the Galois field multiplier generator

Structure of multiplier where MGC is presented as one whole element and as multiplier and adder is described in [9], where MGC consist of simple logic gates in [8].

The process of generating multipliers is divided into the following stages:

• •    Formation of Boolean functions for units;

• •    Minimization of these functions;

• •    Formation of units:

SUM (an adder);

MUL (a multilpier);

F = (-Gm)mod d, d – field characteristic, Gm – output of MGC or SUM or MUL;

SMn (an element that performs modular multiplication and addition and has result and carry outputs);

SMch (an element that performs the operation of adding or subtracting a number in the complementary code during division without restoring the remainder;

Sn (an element that defines the type of operation, subtraction or addition, during dividing without restoring remainders;

Rn (an element that determines whether one more addition operation is required to find the result (only for variants 2 and 3);

• •   Formation of MGC;

• •    Establishing connections between units (multiplier formation).

When forming Boolean functions, the generator automatically generates them according to the truth tables. Next step is Boolean functions minimization by Quine–McCluskey method. Then, on the basis of Boolean functions, units F, SUM, MUL, SMn, SMch, Sn, Rn [23] are formed in the VHDL description language. When forming a modified Guild cell, its VHDL description is generated. Then VHDL description of the multiplier is formed, which describes connections between a large number of MGC and F elements.

The Tab. 2 describes the software implementation of the generator. Table show classes for each variant separately. All data exchange is through files.

Table 2. Classes in GF generator for 3 structurs of multiplier.

MGC is a whole element	MGC consists of a multiplier and an adder	MGC consists of simple logic gates
transformation_and_minimization	transformation_and_minimization	transformation_and_minimization
generateFunctionsForF	generateFunctionsForF	generateFunctionsForF
create_f	create_f	create_f
MGC	MGC	MGC
create_MGC	create_MGC	create_MGC
generateFunctionsForMGC	-	-
MGC	MGC	MGC
create_MGC	create_MGC	create_MGC
creating_matrix	creating_matrix	creating_matrix
	generateFunctionsForMUL	generateFunctionsForSMch
	create_MUL	create_SMch
	generateFunctionsForSUM	generateFunctionsForSMn
	create_SUM	create_SMn
		generateFunctionsForSn
		create_Sn
		generateFunctionsForRn
		create_Rn
		generateFunctionsForAdder
		create_Adder

For 1^st variant, Boolean functions of F and MGC elements are formed in the generateFunctionsForF and generateFunctionsForMGC classes, respectively. Generated functions are written to files. The transformation_and_minimization class then reads these functions from the file and minimizes them using the Quine-McCluskey method [33] and writes them back to these files. The create f and create MGC classes form VHDL templates for descriptions of F and MGC units based on minimized Boolean functions and write them to files. The felement and MGCclasses are the corresponding units F and MGC, from which the create_matrix class forms a matrix.

Classes MGC and F form connections between units.

For variant 2-unit F is formed similarly to variant 1. The MGC block is formed on the basis of MUL and SUM blocks, for which Boolean functions are formed in the generateFunctionForMUL and generateFunctionForSUM classes, respectively. These functions are written to a file. Then they are minimized by the transformation_and_minimization class. The Create_MUL and Create_SUM classes form a VHDL description of the MUL and SUM units. Next, the create_matrix class forms a multiplier.

For variant 3 the structure of the MGC is completely different, but the approach to creating the multiplication matrix is the same. This variant uses generateFunctionForSMch, generateFunctionForSMn, generateFunctionForSn, generateFunctionForRn, generateFunctionForSUM classes. The transformation_and_minimization class minimizes these functions. The classes Create_SMch, Create_SMn, Create_Sn, CreateRn and Create_SUM form VHDL descriptions of these units. The SMch and SMn units are complex because they form the matrix for large MGCs. Then, on the basis of the created MGC, a multiplier is formed.

Fig.6. Galois field multiplier generator interface

In the Fig. 6 we can see the interface of the multiplier generator. It is possible to set the field characteristic as prime number from 2 to 2998 and the polinomial degree from 2 to 998, but with an order near 2998 (see Table. 1) or less. There are three buttons for generating according to three variants. The process of generating Galois field (see Table. 1) multipliers are quite time consuming and can take from a few minutes to several hours.

In Fig. 7 the scheme of synthesized in Xilinx Vivado multiplier GF(73) of the MGC which consists of a multiplier and an adder is shown. Fig. 8 shows the multiplier diagram.

Some multipliers were generated by the generator and the synthesized circuits in Xilinx Vivado environment were analyzed. We will analyze the generated multipliers in the implementation of the MGC as one element, the MGC consisting of a multiplier and an adder and MGC which is a circuit that consists of simple logic gates. A fairly large number of MGCs makes it very difficult to create these multipliers by hand. Millions of MGCs are practically used on multipliers (Table 1).

Fig.7. The scheme of the multiplier GF(73) in the implementation of the MGC as one element

Fig.8. Scheme of the MGC in the implementation

• 8.    Comparison of Hardware Complexity of Generated Multipliers

  In the table 3 and 3a, the real results and theoretical results of generation of multiplier VHDL-descriptions for FPGA Virtex UltraScale+ XCVU9P [34] are presented. This FPGA has 2069000 LUTs. In the implementation of multipliers with MGC, which is a whole element, of their hardware costs increase rapidly with increasing field order. These costs are the lowest for Galois binary and ternary fields. In the implementation of the MGC, which consists of a multiplier and an adder, the hardware costs also increase rapidly with increasing field order. The lowest hardware costs for this architecture are for fields with characteristics d = 2, 3, 5, 7. In the implementation of MGC multipliers by architecture, when MGC consists of simple logic gates, the hardware costs increase with the increase of the field order. Therefore, according to three mentioned architectures it is possible to build any multiplier. Table shows multiplier generation time too. Time increases with raising field characteristic. All measurements were taken in computer with such characteristics:

CPU: Intel(R) Core(TM) i5-3570 CPU;

frequency: 3.40 GHz;

memory: 16 GB;

Windows 10, 64 bits.

Table 3. Multipliers hardware costs as LUT amount NRd, NTd and generation time of Galois field multipliers on for FPGA Virtex UltraScale+ XCVU9P that has 2069000 LUTs (for fields with relatively small order)

The field for which FPGA multiplier is built	d	Galois field order (approxim ately, Od)	MGC is a whole element			MGC consists of a multiplier and an adder			MGC consists of simple logic gates
			LUT amount, NRd	Generati on time, sec.	LUT amount, NTd	LUT amount, NRd	Generati on time, sec.	LUT amount, NTd	LUT amount, NRd	Generati on time, sec.	LUT amount, NTd
GF(250)	2	1,12E+15	2504	1,0	4901	2190	0,5	2450	18784	0,5	29208
GF(332)	3	1,85E+15	4034	1,4	3970	4032	0,7	1984	17950	0,5	36510
GF(522)	5	2,38E+15	19936	1,6	41625	5615	0,8	2768	17867	0,5	35049
GF(718)	7	1,62E+15	16851	3,0	27585	3522	1,2	1837	16689	0,5	23366
GF(1314)	13	3,93E+15	32134	8,0	185420	10211	2,0	10216	15369	0,5	23658

Table 4 and Table 4a show a comparison of theoretical KTmul and real KRmul hardware costs of multiplier as their relationship with KT2 and KR2 costs of multiplier for binary fields when MGC are implementing according to 3 variants. KTmul = NTd/NT2, KRmul = NRd/NR2. It can be seen from the Table 4 and Table 4a and graphs Fig. 9, that when the MGC is implemented as a whole element, ternary Galois fields are 3 % better than binary ones. When implementing a multiplier with MGC that consists of a multiplier and an adder, then compared to a binary field, the field with characteristic 3 has a 11 % bigger cost index, the field with characteristic 5 has a 20 % bigger cost index, the field with characteristic 7 has a 18 % bigger cost index.

Table 4. Multipliers theoretical and real hardware costs comparison on for FPGA Virtex UltraScale+ XCVU9P that has 2069000 LUTs (for fields with relatively small order)

Field	d	Galois field order (Od)	Od г = — °   O2	MGC is a whole element				MGC consists of a multiplier and an adder				MGC consists of simple logic gates
				f^mul	KTmul Co	™mul	™mul Co	^^mul	^Tmul Co	™mul	Omnl	^^mul	Zf^mul	f«mul	f«mul
											Co		Co		Co
GF(250)	2	1,12E+15	1	1	1	1	1	1	1	1	1	1	1	1	1
GF(332)	3	1,85E+15	1,65	0,81	0,43	1,61	0,97	0,81	0,49	1,84	1,11	1,25	0.75	0,95	0,57
GF(522)	5	2,38E+15	2,12	8,49	4	7,96	3,75	1,13	0,53	2,56	1,2	1,2	0,56	0.95	0,44
GF(718)	7	1,62E+15	1,35	5,63	4,17	6,72	4,97	0,75	0,55	1,6	1,18	0,8	0,59	0,88	0,65
GF(1314)	13	3,93E+15	3,5	37,8	10,8	12,83	3,66	4,17	1,19	4,65	1,32	0,81	0,23	0.81	0,23

Table 3a. Multipliers hardware costs as LUT amount NRd, NTd and generation time of Galois field multipliers on for FPGA Virtex UltraScale+ XCVU9P that has 2069000 LUTs (for fields with relatively high order)

The field for which FPGA multiplier is built	d	Galois field order (approximate ly, Od)	MGC is a whole element			MGC consists of a multiplier and an adder			MGC consists of simple logic gates
			LUT amount, Nd	Generati on time, sec.	LUT amount, NTd	LUT amount , Nd	Generat ion time, sec.	LUT amount, NTd	LUT amount, Nd	Gener ation time, sec.	LUT amount, NTd
GF(2998)	2	2,67E+300	1013715	98	1990013	888165	52	995006	not fit	57	15920104
GF(13270)	13	5,81E+300	not fit	889	75222491	not fit	423	4149177	not fit	61	12895284

Table 4а. Multipliers theoretical and real hardware costs comparison on for FPGA Virtex UltraScale+ XCVU9P that has 2069000 LUTs (for fields with relatively high order)

Field	d	Galois field order (Od)	Оа Г = °   O2	MGC is a whole element				MGC consists of a multiplier and an adder				MGC consists of simple logic gates
				^^mul	^^mul Co	^«mul	^«mul	^^mul	^^mul	^«mul	^«mul	^^mul	^^mul	^«mul	^«mul
							Co		Co		Co		Co		Co
GF(2998)	2	2,67E+300	1	1	1	1	1	1	1	1	1	1	1	1	1
GF(13270)	13	5,81E+300	3,5	37,8	10,8	-	-	4,17	1,19	-	-	0,81	0,23	-	-

Fig.9. Comparison of theoretical and real hardware complexity coefficient in 3 variants of GF Multiplier realization

• 9.    Conclusions and Future Scope

The paper summarized the theoretical foundations of creating Galois field multipliers on FPGAs. 3 variants for constructing Galois field multipliers were given, and a comparison of these variants was given. A tool was developed for generating VHDL-descriptions of multipliers of elements of such fields for further use of these descriptions in the implementation of data protection devices on FPGAs.

Hardware complexity was chosen as the criterion for comparing Galois field multipliers. The paper shows that extended Galois fields GF(dm) with characteristics d > 2 are advisable to use in data protection tools, since the particular complexity of fields with characteristic d = 3 Galois fields is 3 % better than that of fields with characteristic d = 2 when implementing MGC as a whole element.

When the MGC consists of a multiplier and an adder, fields with characteristic d = 3 have 11 %, fields with characteristic d = 5 have 20 %, and fields with characteristic d = 7 have 18 % higher indicators of hardware complexity then binary fields.

The article shows the architecture and results of the Galois field multiplier core generator with different order up to 9,49e+300 elements. This generator allows you to generate multipliers VHDL-descriptions that would be almost impossible to create manually. The generator forms descriptions of multipliers that consist of MGC. 3 MGC construction variants are also proposed. The implementation of MGC as a whole element and multiplier and adder has advantages in fields with characteristics d = 2, 3, 5, 7.

The implementation of MGC as a matrix multiplier and adder has advantages in the implementation of a multiplier with large field characteristic. The generation time of vhdl-descriptions can reach 889 seconds. It is also planned to create pipeline cores.