Game Theory - basis of Higher Education and Teaching Organization

At the Higher school the aim of teaching of a concrete subject is to pass the knowledge in this field, its perception and the right to the students. Such a process is realized in conditions of interrelations of the students and the pedagogue. The main task of the subject teacher (professor) is to manifest the student’s personality the solution of which is possible in the process of teaching of the subject in conditions of efficient interrelations with the students by him. And this is still in charge of only professional pedagogue. Here, the notion of a professional pedagogue implies both the knowledge of a specific subject and the pedagogical art and experience, i.e., in conditions of communication with the students to transform each student from the object of teaching into learning of subject. And this depends on the style of management of the students’ collective by a pedagogue, i.e. on the model of their interaction. From various models (such are the authoritarian, liberal, democratic) of interrelation of a pedagogue and the student the most optimal is a democratic model. It implies the objective mutual responsibility of a pedagogue and a student to the objective rights and obligations imposed on them, participation of a student during the whole period of teaching of the subject both during the processingdiscussion of the topics stipulated by the program and during the looking for the ways of solution of the problems existing before the whole group. In such a case we receive a great moral satisfaction - maximal utility by the process and the results of labor. In case of choosing of such a model of management in the group of students, the students establish the close contacts with each other, they have a high sense of responsibility and self-control towards the common affair and there is vividly seen the satisfaction of each student in the successes of students of the same group. A pedagogue of a democratic style tries to envisage the individual peculiarities of the students by means of which the organizational influence on a group of students will be higher than the disciplinary one.

While working with the students the pedagogue, as a human being may have some sympathy or antipathy towards a student which can be caused by behavior of the student or by the results of his work. It’s truth that a pedagogue likes the “clever” students, those who do not miss the lectures-seminars, who systematically study the new explained material, fulfill the home-works and read the additional literature. In such cases the “clever” students get the positive assessments without a problem. This means that the benefit of a pedagogue by their work is increased and his decisions are adequate, too. Why do the others find it difficult? Because they do not think of those interactions and creation of a balanced surrounding by which it would increase the benefit both of them and the pedagogue. That is why, in case of choosing of a democratic model of relation with the students revealing the sympathy or antipathy towards the students should be considered as a normal circumstance and nobody can argue a pedagogue so as he is objective. It means that revealing of such an antipathy is unnoticeable in reality. For the success of the group it is desirable that the sympathy of the teacher were expressed for the absolute majority of the members of the group and the lesser are others much more is the benefit of a pedagogue and of the group itself. So as again with allowance of the human validities, existence even of one student in the group of so called second category influences on the successes of the whole group. That means that the behavior of each student in case of a democratic pedagogue influences on the success of other partners and of the whole group.

Stipulation of all above-indicated is especially noteworthy in conditions of reforms implemented at the Georgian Universities. In the model of democratic relation of the pedagogue with the students it should be envisaged the continuous work of the students for preparing of the lectures-seminars so as during the semester it is required to carry out (to hold) the several intermediate exams. And some students do not do it, or he is not able to do it. Because of this an objective and a respectable teacher will frequently appear in conditions of ambiguity and a decision received by him will not be always acceptable for all students or some pedagogues. By such a formal circumstance often enjoys extremely the “Loyal professor” who neither enforces himself to do the usual heavy labor characteristic for a pedagogue of higher school nor enforce the students to bother themselves - he will realize their wish wonderfully and without any offence. And this will reflect badly on that local collective on the activity and authority of the objective pedagogue. That is why that the whole efforts of the Universities should be directed to establishing the democratic models and organization of teaching of each subject. Such models and organization should be transformed into principle task of each pedagogue and a student, solution of which and results will depend in each specific situation on the degree of decision received by each participant.

• II.    Modeling Of Teaching Organization

At the higher educational Institution under organization of teaching of the subject we mean the organizational functioning of S system which comprises P -pedagogue (professor) and K collective of students. Thus, the interests of the participants (elements) of S system are connected with the quality of functioning of S system. Naturally, in the role of teaching organizational system we can consider as well, the University, faculty, department. Than our S system will be its one of the organizational subsystems.

For organization of S system management the following two circumstances are essential: it is functioning for the definite aim, i.e. the system has its interest; each of its participants has his own interest and their interests, generally, differ both from each other and in integrity from S interest. Mainly, these two circumstances give us the ground that to consider the mathematical model of its some aspects for optimal functioning of S by using of game theory so as in this system there participate several individuals (player, party) having the different interests who can choose one or several actions - strategy. Having realized the corresponding actions, finally they will get profit or pay the penalties. Aim of the players is to choose the optimal strategies by means of which they will get the maximal utility.

The Game theory is a modern, rapidly developing field of the mathematical theory for receiving a decision [1,2,3,4]. From the point of view of a mathematical description under the receiving of the decision it is meant choosing of u element (strategy) from the definite U set. In this relation it is defined a rule of choosing and expediency of u ∈ U element. The complete mathematical theory of receiving the optimal (rational, expedient) decisions in case of participation of several individuals (or party) is a “Game Theory”. The Theory of Games is defined as a mathematical theory of receiving the decisions in conditions of conflict. Contently (semantically) under “conflict we should mean such a phenomenon about which we can say, who and how does he participate in this phenomenon, what kind of results can have this phenomenon, who and how are interested in these results”. Thus, the Game Theory studies any form of social contradiction - differences of ideas, strategic (nonantagonistic and antagonistic), cooperation. In the Game Theory for all these forms there are labored out the mechanisms of fair solutions in conditions of the conflict i.e. the mechanisms of optimal solution.

Traditionally, game theory has been seen as a theory of how rational actors behave [5]. Game theory, the mathematical theory of how to analyze games and how to play them optimally. Although “game” usually implies fun and leisure, game theory is a serious branch of mathematics. Games like blackjack, poker, and chess are obvious examples, but there are many other situations that can be formulated as games. Whenever rational people must make decisions within a framework of strict and known rules, and where each player gets a payoff based on the decisions of all the players, we have a game. The theory was initiated by mathematicians in the first half of the last century, but since then much research in game theory has been done outside of mathematics [6].

It should be noted that in general the game is a special form of transformation of creative work of a human being. It was originated together with the mankind and helped a man to assimilate with the surrounding world both from the objective and social points of view. Gradually, the game has so improved that it obtained a form of conflict relations of several players. The games by their main notions (players, strategies, and payoff) have become a model of a real life of the people and at present they constitute the integral part of any civilization which is approved by the practical creative work of the mankind.

Game theory begins with simple examples, using them to develop general principles that assist in superior decision making. The predictions of game theory give us a baseline for understanding the decisions we make in everyday life [7]. Game theory is the formal analysis of the behavior of interacting individuals. The crucial feature of an interactive situation is that the consequences of the actions of an individual depend (also) on the actions of other individuals. This is typical of many games people play for fun, such as chess or poker. Hence, interactive situations are called "games" and interactive individuals are called "players". If a player’s behavior is intentional and he is aware of the interaction (which is not always the case), he should try and anticipate the behavior of other players. This is the essence of strategic thinking [8].

Game theory is also a branch of computer science. Games provide mathematical models for interaction. Numerous tas Game playing is a powerful metaphor that fits many situations where interaction between autonomous agents plays a central role. Numerous tasks in computer science, such as design, synthesis, verification, testing, query evaluation, planning, etc. can be formulated in game-theoretic terms. Viewing them abstractly as games reveals the underlying algorithmic questions, and helps to clarify relationships between problem domains. As an organisational principle, games offer a fresh and intuitive way of thinking through complex issues. As a result mathematical models of games play an increasingly important role in a number of scientific disciplines and, in particular, in many branches of computer science. One of the scientific communities studying and applying games in computer science has formed around the European Network ‘Games for Design and Verification’ (GAMES), which proposes a research and training programme for the design and verification of computing systems, using a methodology that is based on the interplay of finite and infinite games, mathematical logic and automata theory [9].

The greatest importance of the game is identified for the educational system. By the words of one of the founders of Game theory, the winner of Nobel prize, John Nash “The Game Theory plaid an important role in the intellectual life of the 20th century”.

Game theory helps us to solve the different problems of everyday life. The question is: why only mathematics helps us to solve the above stated problems. Because, the nature is innately mathematical and she speaks to us in mathematics. We should only listen to her. Therefore, any science that describes the nature is completely dependent on mathematics. Mathematics plays a great role and it is the essential instrument for many aspects of different sciences [10]. At the same time Game Theory is one of the largest part of the information culture. Therefore it has a great influence on modern education. In the article [11] the influence of educational, professionalism and activity pecularites has been studied on the formation of the personal information culture pecularities.

There are many learning methodologies that have been adopted down the years. One of them is Problem Based Learning (PBL). PBL is an approach, in which the learners first encounter the problem, followed by a systematic, student-centered inquiry process. In general, games and simulations provide rich learning environment for the students [12]. The purpose of the present research is to designate the effects of Scratch-based game activities on students’ attitudes towards learning computer programming, self-efficacy beliefs and levels of academic achievement [13].

Many professors have inflexible rules not to give makeup exams and never to acceptl ate submission of problem sets or term papers. Students think the professors must be really hardhearted to behave in this way. The true strategic reason is often exactly the opposite. Most professors are kindhearted and would like to give their students every reasonable break and accept any reasonable excuse. The trouble lies in judging what is reasonable. It is hard to distinguish between similar excuses and almost impossible to veriff their truth. The professor knows that on each occasion he will end up by giving the student the benefit of the doubt. But the professor also knows that this is a slippery slope. As the students come to know that the professor is a soft touch, they will procrastinate more and produce ever-flimsier excuses. Deadlines will cease to mean anything, and examinations will become a chaotic mix of postponements and makeup tests. Often the only way to avoid this slippery slope is to refuse to take even the first step down it. Refusal to accept any excuses at all is the only realistic alternative to accepting them all. By making an advance commitment to the "no excuses" strategy, the professor avoids the temptation to give in to all. But how can a softhearted professor maintain such a hardhearted commitment? He must find some way to make a refusal firm and credible. The simplest way is to hide behind an administrative procedure or university-wide policy. "l wish I could accept your excuse, but the university won't let me" not only puts the professor in a nicer light, but removes the temptation by genuinely leaving him no choice in the matter. Of course, the rules may be made by the same collectivity of professors as hides behind them but, once made, no individual professor can unmake the rule in any particular instance. If the university does not provide such a general shield, then the professor can try to make up commitment devices of his own. For example, he can make a clear and firm announcement of the policy at the beginning of the course. Any time an individual student asks for an exception, he can invoke a fairness principle, saying, "If I do this for you, I would have to do it for everyone. "Or the professor can acquire a reputation for toughness by acting tough a few times. This may be an unpleasantt hing for him to do and it may run against his true inclination, but it helps in the long run over his whole career. If a professor is believed to be tough, few students will try excuses on him, so he will actually suffer less pain in denying them [14].

As a consequence of the brought definitions in the mathematical model of functioning of S system there should participate the components participating in this process: 1. Players; 2. The sets of strategies of each player; 3. Interests of the players, expressed privileges, benefits (winnings, payoffs).

Let’s build a noncooperative i.e. noncoalition game model corresponding to game management of S system with participation of three components. Such a model is a strategic version which depicts such an image of a conflict situation in which the players have the discerning interests and choose their interest independently. And here arises a question: Do we have a conflict situation in S system and whether its solution depends on the system’s management? It is clear that the difference of interests of a pedagogue and the students arises as soon as there appears an issue of checking the student’s knowledge and examination. So as the democratic management (functioning) of S system undermines the work and activity both of the pedagogue and a student during the whole semester, besides, the students have to pass several intermediate and final exams, and some of the students has to fulfill the restorations; naturally, the “conflict” in mathematical language lasts for the whole semester. The “Conflict” of such a type deepens the psychological stress of the students so as they have appeared in such a circumstance after school for the first time. At the same time the chosen strategy of separate student, whether it concerns a behavior or activity in subject, influences on decisions of others, too, and that is why it is justified the consideration of strategic (and not of cooperative) model of Game.

We should note that in our game the players are a pedagogue P and a students’ group K . Let’s say that in group K there is n student and it is a set K = {1,2,..., n}. Let it be that the number of a pedagogue, as a player’s is 0. Thus the given organizational system is functioning by the player n + 1 and let’s indicate this set thus: N = P u K = {0,1,2,..., n }.

Let’s define the finite sets of each i e N ( i = 0,1,..., n ) player’s strategies of N set of the players: X X ... X . It is meant that the elements of these sets ₀,     ₁,...,      _n .

i.e. the strategies depend on various factors (are the functions of the factors) from which we’ll distinguish the main, such are: the general education and skills; the contributory material environment (state of studying auditory, teaching of methodical literature and the engineering tools); erudition and technical world-view; psychological state, social state. In the role of X set of the pedagogue’s strategies let’s consider the volume of knowledge to be chosen from the material to be studied envisaged by the program of the subject. k,lcX = Га °- X 1 , where a⁰- and b° are

°°   ^ min, max J               min         ^max relatively that volumes of that minimal and maximal knowledge which is possible for the teacher to deliver from program to the group of students. The set of strategies          {x(;( x =Гamn, bmx J          of i e N(i = 1,2,..., n) student is that volume of knowledge, part of which he should acquire, and simultaneously, the following terms should be fulfilled a min — a min ’ bmax — b max ’ i 1’2’

...

, n. .     (1)

By choosing the x, e X_t strategy of each i e N(i = 0,1,2,..., n ) player the following situation will be received:

x = ( x ₀, x 1 ,...,x_n ) e X = П X i .         ⁽²⁾

i e N

As we are already sure, in the process of laboring out the decision a man makes favor of his privileges i.e.

chooses such an action which, in his opinion will take him to the most privileged result for him. For definition of the individual privileges mainly are used two means – a binary relation and the function of benefit.

It is clear that in conditions of our task each player should be able to clear up from any two situations which is the privileged, i.e., for each i e N player the quality privilege on the X set of the situations should be defined by means of binary relation.

Definition 1. The binary relation R of i e N player to the X set of situations is called a subset of X x X Descartes production r _e x _x X . If ( x , y ) e R than we can say that relation R is fulfilled and we write xR y .

The relation r may be nonstrict - > , strict - ^ or i ii equivalence «4 .We mean that R; for each i e N - on the X - is a privilege: 1) It is finite, which means that for Vx,y e X is xRty or yRx ; 2) It is transit, i.e. for Vx, y e X from that xR,y and yRz, follows xRz .

With allowance of all above-indicated let’s define a system.

Г =< N ,{ X i } i e N ,{ R i } i e N >  (3)

which is a Game model corresponding to S system management - noncooperative game with the preferences of players. And in such a Game the main principle is an equilibrium situation of Nash.

Let’s define the principle of optimality for receiving a decision in Г game. In noncooperative games the main principle of optimality is the Nash’s equilibrium situation or the Nash equilibrium.

For i e N player, x e X situation and x_t e X_t strategy let’s indicate the following:

x-i = (x1’...,x-1,x+1’...,xn), x = (xi.,x_i).

*

Definition 2. The situation x e X is called a Nash equilibrium situation in Г game if for V i e N and V x_t e X_t it is fulfilled x * R _; ( x, , x *, ) .

Thus, if x ^* is the Nash equilibrium than for none of the player it is not profitable the unilateral deviation from it. In real tasks of receiving the decisions, in particular, for description of interests of the players in game (1) it is definitely inconvenient using of binary relations. That is why, there is mostly used the utility function. In noncoalition game (3) we should represent the interests of players with such functions.

The utility functions, their existence, problems of their finding and using are studied in the utility theory which is a constituting mathematical discipline of the game theory. The utility function will comply each alternative (or situation) to a real number - utility of this alternative and it performs a monotonic transformation of set aggregate into real set.

Definition 3. The function H having the defined real valued on X set of situations is called the utility function of i ∈ N player if for ∀ x , y ∈ X one of the terms is fulfilled:

x≥i y⇔Hi(x)≥Hi(y);

x ^ i y ^ H, (x) > H, (y); (4) x≈i y⇔Hi(x) =Hi(y).

Let’s note that the utility function for the given binary R preference can’t exist on any x set. Which conditions should satisfy R that instead of it we shall consider the utility function? Such tasks as we’ve mentioned above are studied in the utility theory and the first theorem about the utility function will be affirmed by J. von Neuman and O. Morgenshtern [1].

Let’s admit that in game (3) for the set of X each i ∈ N ( i = 0,1,2,..., n ) player has a utility function H . Than the corresponding model

Γ ( H ) =< N ,{ X i } i ∈ N ,{ H i } i ∈ N >  (5)

will be a noncooperative game of a normal form (or with functions of payoff, winning).

The Nash equilibrium for the game (5) with the functions of payoff (the 2nd definition) will be formed as follows.

Definition 4. The situation x ^* ∈ X is called the Nash equilibrium situation in Γ( H ) game if for ∀ i ∈ N and ∀ x_i ∈ X_i is fulfilled H_i ( x ^*) ≥ H_i ( x_i , x _- ^* _i ).

The traditional explanation for when and why equilibrium arises is that it results from analysis and introspection by the players in a situation where the rules of the game, the rationality of the players, and the players' payoff functions are all common knowledge. Both conceptually and empirically, this theory has many problems. Drew Fudenberg and David Levine develop an alternative explanation that equilibrium arises as the longrun outcome of a process in which less than fully rational players grope for optimality over time. The models they explore provide a foundation for equilibrium theory and suggest useful ways for economists to evaluate and modify traditional equilibrium concepts [15] .

As from the given definitions is seen the theory of profitability is one of the main methods for a quantitative measurement (assessments) of situations, objects and various validities by which are interested many fields of science. From consideration of (3) - (5) games it is vividly seen that knowing of the elements of this theory is useful on all stages of higher education not only for carrying out the teaching process by the validity principles. That is why that at the known Universities of the world the students of various specialties will study the theory for receiving a decision and its various directions on the basis of theory of benefits. Their initials are studied also at the USA with the aim that the children acquire the art of making the choice. Such circumstances themselves require from each pedagogue, especially from the professor of higher educational school a fundamental knowledge of even the elements of receiving the decisions.

For example, in [16] it’s worth noting that the present paper lies within the range of modeling the learner in adaptive educational system as a conceptual modeling of the learner. Thought they are several methods that deal with the learner model; like stereotypes methods or learner profile…, but they are likely unable to handle the uncertainty embedded in the dynamic modeling of the learner. The present paper aims at studding different models and approaches to model the learner in an adaptive educational systems, and coming up with the most appropriate method based on the dynamic aspect of this model. The aim of this study is the argue that the learner model cannot be completely modeled based on one single method through the entire development process, but it needs a combination between several methods that will help for a complete modeling.

• III.    Problems

In case of two players the model (5) is a bimatrix game and let’s use it in the process of examination.

Problem 1 (Model of examination of a student). Let’s say that the student (the 1^st player) is preparing for the examination with the aim to receive the desirable assessment. The examination is received by a pedagogue (the 2^nd player). Let’s consider that a student has strategies: 1. - to be prepared accordingly (dully), 2 - do not be prepared. A pedagogue has two strategies too: 1 -to give the student a positive assessment, 2 - not to put him a positive assessment. What kind are their optimal decisions?

Compiling and analysis of the model. Let’s draw up the model. We have 4 situations (1,1), (1,2), (2,1), (2,2). Let’s evaluate them. The situation (1,1) indicates that a student has been prepared dully and the pedagogue put him the corresponding mark. In this case let’s evaluate a benefit of a student and a pedagogue accordingly by 2 and 0. Thus, in (1,1) situation the pair of their payoffs (winnings) is (2,0). It is clear that the situation (1,2) (a student has been prepared, and the pedagogue did not put him the mark) is forbidden for the student which we express by (-1) utility, and the benefit of the pedagogue, so he revealed unfairness and it influences on his authority negatively, we shall evaluate it by (-2) . we have received that in situation (1,2) student the winnings of the players are given by the pair of numbers (-1,-2). In situation (2,1) (the student has not been prepared but the pedagogue either was self-deception or because of other causes put him a mark) the student’s utility is positive and let’s say that it is 1, and the benefit of the teacher, in comparison to previous case is much more negative for his authority, which let’s assess by (—3). In situation (2,2) - a student has not been prepared and a teacher assessed correspondingly - neither losses nor wins. Let it be that his utility is 0. And the professor by visiting of the student repeatedly should work additionally, what makes his benefit negative and let’s assess him by (— 1) . Thus, we have bimatrix game:

( H 1 , H 2 )

Г (2,0)

I (1,-3)

(-1,-2)) (0,—1) J.

Let’s solve the game in graphical manner [3, p. 154].

Here, a = 0,5 and в = 0,5. The zigzags are traversed in three points of equilibrium - (1,1), (0,0), (0.5,0.5) (Fig. 1):

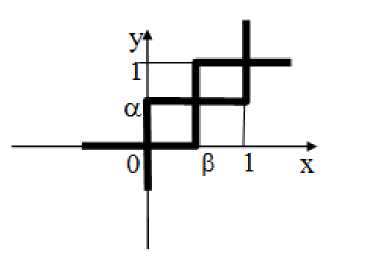
Fig.1. A graphical solution of bimatrix game 2x2

And to them correspond the following situations: a student shall prepare a subject and a teacher should put the corresponding assessment; A student will not prepare a subject and the teacher should deny putting him a desired assessment; The student will prepare a subject at 0.5 probability and the teacher puts him too at the same probability to give him the desired assessment. In the indicated situations there are the utility of the players, correspondingly: (2,0),(0,—1) and (0.5,—1.5).

According to the analysis of the given task for both players it is the best to choose the first strategy - a student should be prepared dully and the teacher will assess his knowledge fairly. Only in this situation both the student and the teacher get a maximal value of the benefit. We have to note that in the indicated model in the role of the 1st player we can imagine as well the whole group, as one player.

The methods of game theory are the nontraditional optimization methods. In game r ( H ) defined by the (2) condition it is meant that the choice of each player envisages the interests of others and thus he performs the optimization of his payoff. In case if any participant of Г ( H ) game, let’s say i * e N will want to receive only his maximal guaranteed benefit without taking into account the others’ interests, than his optimal x ^* decision in i ^*

situation of x = ( x, , x ,)

a min — a min , b max ^{— b} max ,    i = 1,²,..., n   ⁽⁷⁾

the

With allowance of terms, we can define the optimization (of mathematical programming) by solution of following task:

Let’s find maxminH (x ,x ) i       i—

x* x * i— in conditions of:

a min — xi — b max, i = 0J,"', n, i    00

I a min — a min , b max — b max , i   ^1,...^, n ^.

And in Г(H) game the task of finding of the

equilibrium and coalative sustained (in Pareto’s opinion) situations we can write down as a multicriteria task: in conditions of (8) let’s find max(H0(x), H1(x),..., Hn(x)).    (10)

x e X

Functioning of our organizational S system and its optimal management means a rational behavior of the players’ collective which corresponds to the equilibrium and effective situations.

If we consider the functioning and management of S system as a two-level hierarchic game between the center and the agents (between the teacher and the students of the group) in which the first step (run) is made by the first player (center-pedagogue) than for analysis of the task of such a type we can use those conceptions for receiving the optimal decisions which have been processed in the theory of hierarchic games.

In contemporary conditions of teaching process because of various circumstances it is impossible to make the unilateral solution of many organizational problems. Let’s consider the following task.

Problem 2 (Distribution of the scores of weekly assessment). Let’s assume that by decision of the University, a weekly maximal assessment of the student are 2 scores. How can we distribute these 2 scores? It is clear that the assessment of the student should be done by means of the theoretical and practical part of the subject when the professor has a possibility to intercommunicate with a student. In case if the leading professor of the subject does not teach a practical part than he during the weekly assessment of the student should envisage the assessment as well made by the corresponding pedagogue. Let’s undermine that the weekly assessment comprises the following alternatives and their assessments: a -attendance (we mean only attendance without home-work and preparation); a - fulfilling of home-work in practical part; a - preparing of delivered material at medium level; a - preparing the delivered material well. (We can consider as well an alternative of relation of a student with the blackboard).

Compiling and analysis of the model. In the first turn let’s find a weight vector of the given alternatives by using of the method of hierarchic analysis. For this let’s consider the following quality privileges of alternatives and their corresponding quantitative assessments: equally privilege - 1; weakly privilege - 3; strong privilege - 5; very, very strongly privilege - 7; absolute privilege - 9. For finding the weight vector we use [17] and let’s consider the following matrix of assessments of privileges

aaaa a1

SX = a2

a ₃

a ₄

and let’s find the a ₁₂, a ₁₃, a₁₄ assessments. These assessments are found by me – the leading professor of the subject. For me the privilege is the student who submits to me an independently fulfilled practical work than that student who had not done this homework (it is not important its quantity and quality). How shall we depict this privilege? I consider it as a strong privilege (and not as a weak privilege) and that is why a ₁₂ = 1/5. A student who fulfils the lecture material on medium level, I mean mostly the attendance, i.e., a is privileged than a , besides very strongly, i.e. a₁₃ = 1/7. For me it is absolutely privileged a well prepared of the lecture material than the attendance and that is why a ₁₄ = 1/9 ■ According to the method we’ll find accordingly the needed elements of   matrix..

S X

Let’s draw up a vector a 0 = ( 1 ⁵ 7 1 from the final ,,, ( 9 9 9 )

column of S matrix and make its rate-setting. So as 1/9 + 5)9 + 7/9 + 1 = 22/9, that is why the given alternative weight vector a , a , a , a will be as follows:

a = (0.045;0.225;0.315;0.405).

Now let’s distribute these 2 scores according to these weighs:

2 • 0.045 = 0.090 « 0.1; 2 • 0.225 = 0.450 « 0.5;

2 • 0.315 = 0.630 » 0.6; 2 • 0.405 = 0.810 « 0.8.

Thus, if the student has come without the home-works (he has only visited) he will be evaluated by 0.1; If he comes and has fulfilled a practical work he will be assessed by 0.1 + 0.5 = 0.6; If he has come, has prepared a practical home-work on a middle level, he will get the assessment 0.6 + 0.6 = 1.2; If the student has a homework additionally and is prepared well his assessment will be 1.2 + 0.8 = 2.

Here we want to note that the student’s assessment should be as much as possible objective and fair. His promotion is necessary. But here, always should be defined the fair upper limit of such promotion. For unjustified increase of this limit a pedagogue will be punished by all means in future (according to the people’s theorem).

Now, again let’s concern the process of attendance by the students of lecture-seminars and carrying out (performing the process of the dully process). Let’s consider a task.

Problem 3 (The student’s attendance visit - no visit). If the weekly assessment of the student and its indication during the semester influences on his academic progress, than for both parties (student and professor) there arises one more problem for receiving the optimal decision -visit - no visit of the student and assessment – nonassessment of the student by the pedagogue. How should behave a student and how does the professor (this issue must not be problematic as a consequence of his indication but sometimes we can come across the exceptional cases too.)

Compiling of the model and analysis. Let’s admit that in such an interrelation a student, the same the 1^st player has strategies: 1 - to come on demand for the prepared activity; 2 - come to the professor nonprepared; 3 - not attendance at all. A pedagogue of the 2nd player has the lesser number of strategies and they can be: 1 - to assess a student objectively; 2 - to assess a student nonobjectively.

Let’s draw up a model of bimatrix game. We have 6 situations (1,1), (1,2), (2,1), (2,2), (3,1), (3,2). Let’s assess these situations: In situation (1,1) - the student came prepared and the professor has assessed him correspondingly, the assessments of the player, let it be correspondingly 2 and 1; In situation (1,2) because of the pedagogue’s partiality a student is damaged, he can’t receive a positive assessment, and this negatively is reflected on the pedagogue’s authority.The corresponding assessments are 0 and (— 1); In (2,1) situation for both players the justified assessment will be 0; In situation (2,2) - the unprepared student is assessed by the pedagogue positively which does not express positively the partiality decision of the pedagogue. That is why, this assessment for him should be lesser in situation (1,2) than his assessment, that is why let’s indicate the assessment of the 1st by 1 and that of the 2nd by (_2); In situation (3,1) for both the assessment 0 will be justified; For such an exceptional student for which it becomes necessary to consider and analyze of such a model most favorable will be not to come to the lecture and be assessed positively, i.e. the situation (3,2) is more privileged than the situation

(2.2.). Therefore, let’s evaluate the usefulness of situation (3,2) for him (let it be he is evaluated by the professor by any positive score) by the same usefulness which he receives in case of appearing prepared, i.e., by 2. As for the 2^nd player, in situation (3,2) with such a decision received by him he can be appeared in a very awkward situation. That is why his benefits (or payoffs, winnings) should be assessed negatively for violation the various kinds of norms and let it be ( - 3). Therefore, a bimatrix game has the following form:

((21) (0, - 1) )

( H 1 , H 2 ) =   (0,0)  (1, - 2)

( (0,0)  (2, - 3) J

Here dominates the third strategy of the 1st player (student) over the second one, and that is why this latter will be removed and we’ll get a bimatrix game:

( H 1 , H 2 )

Г (2,1)   (0, - 1) ^

I (0,0)  (2, - 3) J

In both situations the only situation (1,1) is equilibrium in pure strategies. By using of graphical method we’ll be easily assured that in a bimatrix game we have no equilibrium situation in mixed strategies. That is why it comes out that neither we have no equilibrium situation in mixed strategies. Thus, the only equilibrium situation in a game in pure strategies (1,1) tells us that for the players there exists the only optimal situation – the student should come to the lectures-seminars prepared and a professor evaluates him objectively.

• IV.    Conclusion

The teaching-learning process is a very tender organism. The decision received wrongly and unjustly in this sphere, let it concerns even low-quality problem, may violate the equilibrium and the process can appear in a chaotic situation coming out from which escape later is impossible. Any reform in educational system or the intra university decisions connected with the process of teaching organization should be solved scientifically, purposefully by the specialists (experts) of the highest level. Otherwise, we’ll receive an equilibrium and unsustainable situation which influences on the whole process of teaching-learning and finally – on the future of the country. By using game theory it is possible to resolve all necessary problems of teaching organisation of a subject.