Гашение энергии потока с применением криволинейной стенки водобоя

Избыточную кинетическую энергию водного потока требуется погасить на укрепленной части водосбросного сооружения. Для гашения волны водосбросного сооружения применяются водобои [1].

Цель исследований . Повышение эффективности гашения энергии водного потока на коротком участке водобоя водосбросного сооружения.

Методы и результаты исследований . Для решения поставленной задачи в водобое водосбросного сооружения на выходе из водобоя предлагается применить водобойный элемент в виде уступа-стенки, напорная поверхность которого выполнена с образованием последовательно чередующихся по длине водобойного элемента впадин и выступов, при этом впадины выполнены вогнутыми, криволинейного очертания.

Параметры образующейся волны могут быть определены путем рассмотрения уравнения сохранения количества движения:

m V = m c

где m 1 , m ₂ - масса жидкости в потоке и формирующейся волне; V , c — скорость потока волны.

Частица m, поднимающаяся от источника, будет смещаться на величину Δ со скоростью V , меньшей, чем скорость V в сжатом сечении потока (рис. 1). Таким образом, волновой бугор в целом будет смещен в сторону нижнего бъефа. Для того чтобы волна формировалась в пределах водобойного сооружения, необходимо обеспечить возникновение источника на расстоянии, превышающем величину Δ от водобойной стенки. Это условие можно обеспечить подбором радиуса закругления криволинейной стенки R .

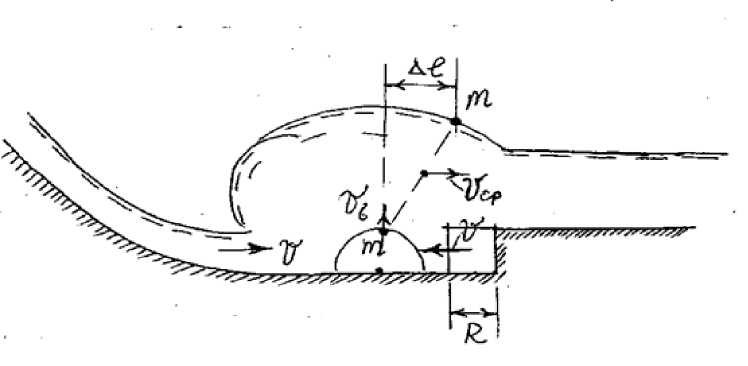
Рис. 1. Формирование стоячей волны конечной амплитуды на водобойном сооружении

Формирование стоячей волны конечной амплитуды на водобойном сооружении возможно путем установки криволинейной стенки (рис. 2).

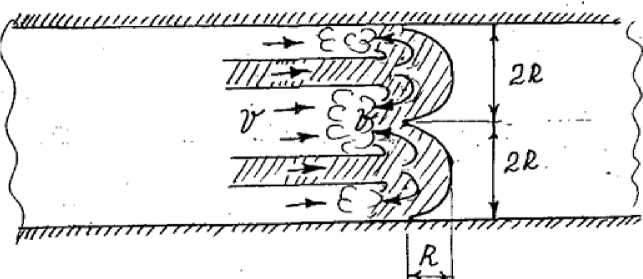
Рис. 2. Расчетная схема водобойного колодца с криволинейной стенкой

Колодец с криволинейной водобойной стенкой позволяет существенно сократить длину колодца, но подвергается более значительным нагрузкам. Наибольшему воздействию подвергаются криволинейные водобойные стенки. Суммарная нагрузка на водобойную стенку может быть представлена следующей формулой [7]:

P s=P1+P2 + P3,

где P – гидростатическое давление, обусловленное возникновением волны, высотой h _в; P – динамическое давление струи на криволинейную стенку высотой a с учетом центробежных сил; P – пульсации гидродинамического давления, которые определяются как сумма составляющих пульсаций гидродинамического давления от взаимодействия волн и как флуктуации струи, набегающей на криволинейную стенку.

^P 1 = Th e .

Согласно [2], для P можно принять выражение:

P 2 = Pf+Pp£ где P υ – динамическое воздействие, обусловленное изменением количества движения жидкости; P  – динами ческое воздействие, обусловленное центробежными силами при обтекании криволинейной поверхности.

Выведем выражение для P динамического воздействия струи на элемент криволинейной стенки. Расчетная схема представлена на рис. 3.

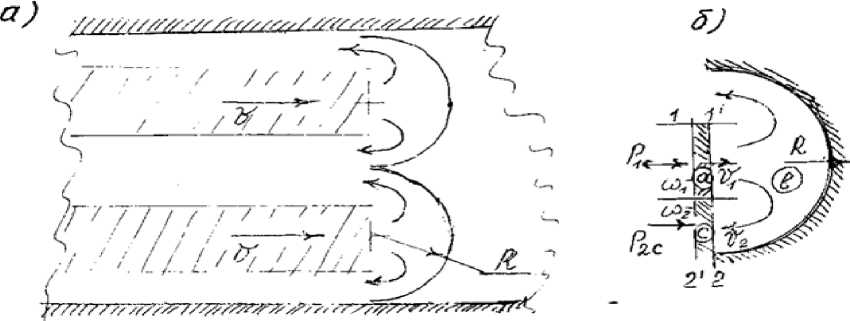
Рис. 3. Расчетная схема водобоя с криволинейной стенкой: а – общая расчетная схема; б – схема набегания потока на один элемент кривизны

Струя набегает на криволинейную стенку со скоростью υ , а сбегает со скоростью υ . Найдем изменение количества движения расхода жидкости при набегании на криволинейную стенку согласно [3].

d ( m u ) = kd ( c ) - kd ( a ) ,

где kd ( c ) — количество движения расхода жидкости при набегании на криволинейную стенку; kd ( а ) -количество движения расхода жидкости при сбегании с криволинейной стенки.

В общем случае для расчетной схемы, представленной на рис. 2, б , будет иметь место неравномерное распределение скоростей [4, 5], т.е. u = u ₂ + s , где и₂ - средняя скорость по сечению ш ₂, е ^0 .

Тогда получим

kd(c) = J (dmu) = pdtj u2 da =pdt (u 2° + J s2 do) =

a           aО

J s 2 do(6)

= pdtu 2 a (1 + °2"!

uou j s2 da где (1 + °2—;----) - коэффициент Буссинеска.

u2o

Если принять d = const , то для схемы рис. 2, б приращение количества движения для выделенной массы жидкости между сечениями 1-1 и 2-2 будет определяться следующим выражением:

pd 0 Qdt(u - U1) = (Pc + P2c + R)dt.(7)

Если принять P =P и υ =0 , то будем иметь

R = -pd0 Qui - P - P2 =-(pd0 Qui + 2 P1) .

Если дуга криволинейной части стенки меньше π , то выражение (8) будет представляться в виде

R = -pdQ(u2 cos a + U cos a2) - P - P2,(8а)

где α , α – углы входа и выхода на криволинейной части.

Для отыскания центробежной силы, воздействующей на криволинейную стенку, воспользуемся зависимостью [2], согласно которой

P2 n = pQlc X — , ст u2 _ где       = an – ускорение потока, обусловленное центробежными силами (нормальное к кривизне стен- ст ки); Rст – радиус закругления стенки; υ – скорость потока обтекания криволинейной части стенки (касательная скорость).

Подставляя (7) и (9) в (3), получаем формулу для P:

P ₂ =, [ - ( P d о Q U + 2 P )]² + [ p Ql c x — ] ² R_ст

P = P, +P„

1 3    2 31 + 1 32, где P – пульсации гидродинамического давления, обусловленные взаимодействием волн;

P – пульсации гидродинамического давления, обусловленные флуктуациями набегающей на криволинейную стенку струи.

Формулы для определения P₃,, p ₂. Нагрузки P j определяются по частотным характеристикам волн и могут быть оценены по приближенным зависимостям:

• - для косинусоидальных волн [6]:

£ = hdi x cos(rt - kx); £2 = hbi x cos(r2t - k2x) ,(12)

где     £ 1 , £₂ - амплитуды двух волн; h_b1, h_b2 - наибольшие амплитуды волн;

2 п с     _ 2 п с 2

А волны;

• λ – длина волны.

При взаимодействии волн (12), если ( ® 1 1 — k 1 x ) = ( ® ₂ 1 — k ₂ x ) = y , имеем величину:

£ = (hb1 + hb2)cos Г(13)

При ( r t — kx ) ^ ( ^₂1 — k₂x ) имеем

δ + δ δ + δ    δ + δ δ + δ

£ = A(sin -1---2 cos----2 + cos—---4 cos—

2        2          22

где    ^ i = [ a — ( r 1 — k 1 x )] ; ^ ₂ = [ a + ( ® 1 t — k 1 x )] ; £₃ = [ a ( ^ t — k₂x )] ;

£₄ = [ a + ( r t — k₂x )] ;

^{sin a} =   /2 ^{b 1}  2 ’^{COs a} =             ’ A = ^ ^hb ^{2 + h}b ²2

V hbl + hb22           hb^+

Оценка нагрузки P целесообразна на основе экспериментальных данных.

Выводы

Преимущество представленного водобоя водосбросного сооружения заключается в более эффективном гашении энергии потока на сравнительно коротком участке за счет формирования отраженных волн, также обеспечивается эффективное гашение гидравлического прыжка в связи с образованием волновых флуктуаций.