Газодинамическая модель внутреннего строения Земли

Внутреннее строение Земли оценивается по известной массе, моменту инерции земного шара и на основе изучения упругих волн от землетрясений. Известно, что плотность вещества в центре Земли р >  12,2 г/см³ и ядро Земли на глубине 2 900 км отделено от лежащих выше слоев резким скачком плотности - порядка 4 г/см³. Таким образом, упругие свойства внутри Земли изменяются скачкообразно на некоторых определенных значениях глубин и плавно - в пределах слоев, разделенных этими границами. Важнейшими границами являются поверхность Мохоровичича, залегающая на глубине 10...70 км, и поверхность Вихерта-Гутенберга на глубине 2 900 км, резко преломляющая продольные упругие волны и не пропускающая поперечных волн. Эти границы разделяют земной шар на три главные зоны: кору, мантию и ядро. Земля образована твердым слоем толщиной примерно равной половине радиуса, и ядром, имеющим два агрегатных состояния - жидкое и твердое. Кора обладает наибольшей жесткостью, мантия характеризуется высокой вязкостью, а ядро находится в состоянии, близком к жидкому, и реагирует лишь на продольные волны изменением объема. Внутри трех главных зон земного шара имеются и менее четко выраженные границы. В последнее время в некоторых работах вводится предположение, что внутреннее вещество Земли ведет себя по отношению к длительно действующим силам как жидкость.

Авторами предлагается математическая модель, позволяющая адаптировать структуру Земли газодинамическим состоянием плотности, динамической вязкости, внутренней энергии и высоких температур. Цинамика геосферы Земли исследуется в рамках модели вязкого сжимаемого газа, когда плотность среды меняется во времени и пространстве. Сферически-симметричное течение вязкого теплопроводного газа рассматривается с учетом гравитационных сил. Уравнения решаются в безразмерной постановке [2], когда линейные размеры отнесены к радиусу Земли, а все газодинамические величины -к соответствующим характерным значениям на поверхности земного шара.

Цля описания процессов сферически-симметричного расширения, сжатия, разогревания и охлаждения Земли используются уравнения Навье-Стокса. Введем сферическую систему координат (г, 6, ф), связанную с декартовыми координатами следующим образом: х = г cos ф sin 6, у = г sin ф sin 6, z = г cos 6, 0<г< + ^,0< 6 < п, 0 < ф < 2п. После записи уравнений Навье-Стокса в сферической системе координат [2] учет сферической симметрии приводит к равенству нулю производных по ф и 6 и компо нент скоростей по ф и 6. В итоге уравнения неразрывности, импульса энергии записываются в следующем без размерном виде:

∂σ 1 ∂          1 ∂σ

+ ( r ² σ u ) + u = 0,

∂ t   2 r ² ∂ r          2 ∂ r

σ ( t , r ) =ρ ( t , r ),

∂ 1 ∂

( ρ u ) +        ( r ² ρ u ²) =

∂ tr ² ∂ r

∂ P   1 ∂

=-    + ₂    ( r ² τ _rr ) + F_em ( r , ρ ),

∂ rr ² ∂ r

∂ 1 ∂

( ρ e ) +        ( r ² u ρ e ) +

∂ tr ² ∂ r

1 ∂

∂ u rr _{∂ r}

1 ∂ ₂1 ∂ ₂

+ P ₂( r ² u ) =- ₂( r ² q_r ) +τ r ² ∂ r           r ² ∂ r

.

Искомыми функциями являются плотность р = о2, скорость и и внутренняя энергия единицы массы е, через которые выражаются давление Р и динамический коэффициент вязкости ц из уравнений состояния, и Fem (r, р) - потенциал гравитационных сил. Уравнения состояния представляют собой сложную алгебраическую зависи мость плотности от давления и температуры с учетом фазовых переходов и метаморфизма основных составляющих веществ. Отметим, что запись уравнения (1) для о, а не для р переводит закон сохранения массы из нормы пространства L1 в норму гильбертового пространства L2. Впоследствии это значительно упростит обоснование устойчивости и сходимости.

Потоковые соотношения, связывающие тензор напряжения т _rr с тензором скоростей деформации и определяющие тепловой поток q_r через безразмерные параметры - число Рейнольдса Re и число Прандтля Pr, выражаются зависимостями

4∂u4

τ _rr =     µ -µ

3Re ∂ r 3 r Re

γ∂e qr =-µ

RePr ∂ r

Потенциал гравитационных сил в данном случае представлен в следующем виде:

Fem = - 4П Fr 41 ^|[р x2dx’ r20

где Fr - число Фруда; х l - безразмерная величина, которая определяется гравитационной постоянной, ускорением свободного падения и плотностью на поверхности Земли.

В качестве начальных условий берутся реальные значения плотности и динамического коэффициента вязкости (см. таблицу) [1].

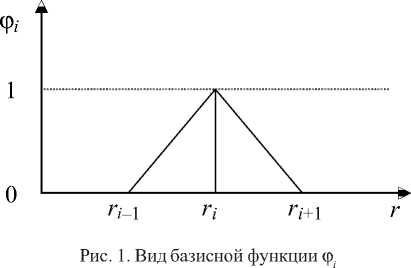
На расчетной области радиус Земли занимает одну четвертую часть, остальные три четвертых приходятся на атмосферу. Введем равномерную сетку r = ( г + 1/2) h , г = - 1,..., n , с шагом h — 2 / (2 n + 1). Обозначим Q _h — { r , i — - 1,..., n } и введем множество внутренних узлов Q h — { r , г — 0,1, ..., n - 1}. В результате расчетная область Q будет разбита на и + 1 интервал ( r , r _{+ 1}), i — - 1, 0,..., n - 1. Для каждого узла r е Q _h определим базисную функцию ф , , которая равна единице в r , нулю во всех остальных узлах Q h и линейна на каждом отрезке ( r , r _{+ 1}) (рис. 1):

Применяя формулу интегрирования по частям к (10), получим равенство

2 . ^до , . ( 1 _ ^         ¹ 2_ ^дФ

I ^- ф i — dr + l-ф i ^о u r —1 ^-| -г ^о u — dr + 0       д t       к 2       j 0 2        д r

+ [- r ²ф_; и — dr — 0, l — 0,..., n .          (11)

0 2     '- д r

Подставим приближенное решение (7) в равенство (11)

вместо о

n ¹

∑⎡⎢∫ i—0 L 0

( до(0 ⎜ _{⎝∂ t}

2 - r ф l ф, -

— r о, u

2      '

* ф+ 1 д r

∂ϕ ⎞ r о, и фl   '- dr +

∂ r ⎠

ф , ( ^r )

- r-1, ес^и г е [r-1, r ], h r+^Tr, ес^и r е (r, r+1 ], h

0, ecto r £ ^[ r - 1 , r +1 ^].

⁺ 2⁽ u ^о , ф l ф , ) r —1

— 0, l — 0,..., n .

С учетом выбора базисных функций (6) отличными от нуля в (12) остаются следующие слагаемые:

l + ¹ Г1

∑^⎡ ⎢ ∫

, — l - 1 L 0

до , ( t ) ∂ t

2 _ _ ^r ф l ф ,

12    дф,      1 2 дф ) ,

- r о,и L ф, + r о,иф   . dr + д r^* 2    1     д r J

⁺ 2^{( и о} , ф l ф , ) к— 1

— 0, l — 0,

..., n .

Для вычисления интегралов в уравнении (13) применим квадратурную формулу трапеций и равенства о -1 — о ₀, и , — - и ₀, вытекающие из симметрии задачи. Аппроксимируя производную по времени правой разностной производной, в итоге получим разностные уравнения:

h k+1

* 0 ^о 0 Т

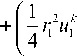
- h 3 n k

^— . ^о 0 ,

4 т

¹ _.2. k

4 ^r 0 ^и 0

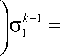
С помощью введенных обозначений сформулируем метод Бубнова-Галеркина. Будем искать приближение о _h ( t , r ) к функции о ( t , r ) в виде

l — 0,

n о h(t,r) = Z°-( t )q(r)                (7)

i =0

с некоторыми коэффициентами о , ( t ), зависящими от времени. Подставим пробное решение о h в уравнение (1) вместо точного решения и умножим скалярно на ф _l :

| ^{- 1} r l -1 ^и ( - 1 ^{- 1} rl^2и ( |^о k ^{+ 1 + 1} r ^{2 h о} k ^{+ 1 +}

I 4          4 J T

, ( ¹ ..2 . k , ¹ ..2. k ’    k +1      ¹ k

⁺ l 4 r l +1 ^Ui +1 ⁺ 4 r l ^Ui  |^о l +1 ^— t r h ^о l ’

l — 1,..., n - 1,

где

( R , ф _l ) = 0,   l — 0, ..., и                 (8)

+

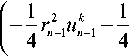
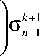
„ до h 1 д _{z 2 х} 1 до h

R —--1--2— (r о .и) +— и--- д t 2 r2 д r     h 2 д r

.

( h 1 2

+ l ^r„ + T rn и„ о n — ^Г„о n , l — n.

T 22

Здесь в нелинейных членах заморожены коэффициенты,

Используя редукцию скалярного произведения из R³ в R¹ при условии сферической симметрии, получим сле

дующее выражение:

известные с предыдущего шага по времени.

Аналогично (7) будем искать функцию и_к ( t , r ), аппроксимирующую функцию и ( t , r ) в виде

г 2 (до J ^{- ф} i к 0 к t

¹ д , 2_₂. 1 до)

—7 — ( - о и ) + — и     dr — 0, l — 0,..., n . (10)

2 r ² д r          2 д r J

n

Ur ( t , r ) — ^ и , ( t ) ф , ( r )

—0

Значение плотности, коэффициента динамической вязкости, давления и температуры внутреннего вещества Земли в размерных величинах

h, км 15 60 100 150 200 300 400 600 1 100 1 600 2 700 2 870 2 900 4 700 6 371 Р, кбар 3,5 14 29 46,5 64,9 99 130 190 30 530 1 240 1 340 1 350 3 040 3 632 Т, К 673 873 1 103 1 343 1 473 1 623 1 673 1 723 1 873 2 700 3 500 4 000 с 2,85 3,34 3,37 3,37 3,36 3,48 3,54 4,13 4,74 5,03 5,55 5,68 9,89 12,3 13,01 м 0,35 0,72 0,72 0,72 0,7 0,75 0,82 1,3 1,7 2,2 2,9 2,95 0 0 с некоторыми коэффициентами и, (t), зависящими от времени. Вновь, используя редукцию скалярного произведения из R3 в R1, в случае сферической симметрии получим следующее выражение:

_r 2 _ϕ⎡⎛ρ∂ u ₊ u ∂ρ ^∫ 0       ^{l ⎢}⎣^⎜⎝∂ t 2 ∂ t

⎞ 1 ∂ ⎟+ ₂ ( r ² ρ u ²) -_⎠ r 2 _∂ r

u ∂

2 r ² ∂ r

2 ∂ P ( r ² ρ u ) +    -

∂ r

ρ uu_i ϕ _l ϕ _i -ϕ _l     µ u

23Re

∂ϕ      4

_i ⁱ +ϕ _l      µ u_i ϕ _i

∂ r    3Re

r =1

2 ∂ϕ _l

∂ϕl⎞⎟dr-(ϕlP)+r2ϕlFemdr, r r⎠                      0

l = 0, ..., n .

1 ∂⎛ 4 2 ∂ u    4

⎜r2µ-rµu r2 ∂r⎝3Re    ∂r 3Re

-

F em

l = 0, ..., n .

d r = 0,

Отметим, что в(16) использовано исходное уравнение (2), из которого вычтено уравнение неразрывности, умноженное на и / 2. Это приведет и в непрерывном, и в дискретном виде к устойчивости в норме пространства L 2 , анев L, как в уравнении (2). Применяя к (16) фор

Для вычисления интегралов в уравнении (19) применим квадратурную формулу трапеций и равенства и -1 = - и ₀, ц _1 = ц ₀, вытекающие из симметрии задачи. Аппроксимируем производную по времени следующим образом:

мулу интегрирования по частям, получим

1    ⎛∂uu∂ρ⎞ r2ϕl⎜ρ +       ⎟dr+(ϕlρu2)

₀       ⎝∂ t 2 ∂ t ⎠

г-1 - J r ²Р u ²      dr - ¹⁽ Ф / Р u ²⁾ г-1 +

0         d r       2

11 2∂

+   r2ρu (ϕlu)dr+(r2ϕlP)

t 2       д r

=ρ l ^∂ ( ∂ t

В итоге получим

⎛ h

2 k +1 ⎜ r ₀ ρ ₀ ⎝^τ

∂ui+ui∂ρl= ρl ∂t2 ∂t k+1 k+1 ρlul-

2 r2µk hRe 00

.

-

τ

r ² µ ^k

3 h Re ¹¹

⎞ k +1 ⎟ u 0 ⁺

1₄ r ₁2 _{ρ 1} k + 1 u ₁ k

-

2 k 2

r µ+ r

3 h Re¹¹ 3Re¹

₁ k ₊ 1_{4 r 0}2 _ρ k ₀ + 1 _{u 0} k

-

2 _r 2 _µ k ⎞ _uk + 1 3 h Re^{00 ⎟}⎠ ¹

1 _⎛ - ∫ P ⎜ 2 r ϕ _l + 0 ⎝

∂ϕ ⎞ r2 l dr ∂r ⎠

-

4 ∂ u

ϕ µ -ϕ l3Re ∂r l3Re

■ +

4∂u   4⎞ r2µ-rµudr-

3Re     ∂ r 3 Re      ^⎟⎠

- J r 2 Ф Vr = 0, 1 = 0,..., n.          (¹⁷)

Подставим приближенное решение (15)в равенство (17) вместо и :

n 1 _∑ ⎡ _⎢∫ i =0 ⎣ 0

ϕ _l ϕ _i

ρ

∂ u_iu_i ∂ρ ∂ t 2 ∂ t

1         ∂ϕ r2ρuuϕ l+ 2ii∂r

0002 1 2 kk 1 k 22 k = hr ₀ + r ₀ P ₀ + hr ₀ P ₀ P ₁ r ₁ + hr ₀ F_{em ,0} , l = 0, 000   00   110 em ,0

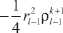
h

τ

2 _r 2 3 h Re ^{l -}

3Re

-

1 2 k + 1 k 2 2 k ⎞ k + 1 r l ρ l u l ^-          r l ^µ l ⎟ u l - 1 ⁺

43 h Re ⎠

k + 1

3 h Re

r 2 _µ k ₊ 3 h Re ^ll

3 h Re

2 k ⎞ k + 1 r l + 1 ^µ l + 1 ⎟ u l    ⁺

k _- 2 r 2 _µ k ₊ 2 r _µ k ₊ 1 r 2 ρ k + 1 u k l + 1               l + 1 l + 1             l + 1 l + 1 ll l

3 h Re       3Re       4

-

3 h Re ^rl

k + 1

⎟ u l + 1

1 2 ∂ϕ + r ² ρ uu_i ⁱ ϕ _l 2 ∂ r

4 2 ∂ϕ l ∂ϕ i

+ r µ u 3Re ⁱ ∂ r ∂ r

-

4 ∂ϕ ⎞

- r µ u ϕ ^l dr + 3Re ⁱⁱ ∂ r ^⎟⎠

⎛ 14 ∂ϕ 4

+⎜ρ uu_i ϕ _l ϕ _i -ϕ _l     µ u_i ⁱ +ϕ _l

⎝ 23Re ∂ r  3Re

r =1

= J P ( ² r Ф/ + r 2 ^ ) dr ^{- (} Ф / P ) _r = i ⁺ J r ²Ф / F em dr , (18) ₀ ⎝∂ r ⎠                      ₀

l = 0, ..., n .

С учетом выбора базисных функций (6) отличными от нуля в (18) остаются следующие слагаемые:

l + 1 1 ∑ ^⎡⎢ ∫ i = l - 1 ⎣ 0

r ² ϕ _l ϕ _i

∂ u i ₊ u i ∂ρ ρ ∂ t 2 ∂ t

⎞ 1 ∂ϕ 1 ∂ϕ

⎟- r ² ρ uu_i ϕ _i ^l + r ² ρ uu_iⁱ ϕ _l +

⎠ 2           ∂ r 2        ∂ r

4 3Re

r ² µ u_i

∂ϕ _l ∂ϕ _i ∂ r ∂ r

4 ∂ϕ ⎞ - r µ u ϕ ^l dr + 3Re ⁱⁱ ∂ r ^⎟⎠

= ρ ^{lk + 1} ρ ^{lk u lk} hr l ² + 1 r l ² -1 P l^k -1 + 2 hr l P l^k -τ            l 2 l 1 l 1 ll

1 2 k 2 k

2 r l +1 P l +1 ⁺ hr i F em , i , l ⁼ 1, ..., n 1,

k+1k n-1 n-1

-

3 h Re

2 k n - 1 ^µ n - 1

-

3Re

^k n - 1

1 2 k + 1 k 2 2 k ⎞ k + 1

- r ρ u -      r µ u +

4 nnn     nnn - 1

3 h Re     ⎠

h 2 k + 1       2 2 k 2 2 k 2 k 1 2 k + 1 k ⎞ k + 1

r n ρ n ⁺ r n - 1 ^µ n - 1 ^- r n ^µ n ⁺ r n ^µ n ⁺ r n ρ n u n ⎟ u n  ⁼

2 τ    3 h Re3 h Re3Re2 ⎠

k +1    kk

ρ _n ρ _nu_n

2 τ

22 k r n ⁺ 2 r n -1 n -1 ⁺

+ hr„P k - 2 rP k + hr„²F ^ , n , / = n.         (²°)

Будем искать приближение h ( ( t , r ) к функции e ( t , r ) в виде

n

h^{( (} t , ^r ) = Z ^ei ⁽ t ) Ф - ^{( r} )                  (21)

i =0

с некоторыми коэффициентами e, ( t ), зависящими от времени.

Используя редукцию скалярного произведения изR3 в R1, в случае сферической симметрии получим следующее выражение:

∫ ⎜ r ² ϕ l 0 ⎝

∂∂∂

( ρ e ) +ϕ _lP ( r ² u ) +ϕ _l ( r ² u ρ e ) -∂ t ∂ r ∂ r

γ∂

RePr ∂ r

∂e⎞ r2µ     ⎟ϕl

∂ r ⎠

-

4₂     ⎛∂ u ⎞ ²    4 ∂ u ⎞

- r ² ϕµ+ r ϕµ u dr = 0, 3Re    Чд r I 3Re ¹ д r J (22)

_- 2 _{r µ} k _u k +1_{( u} k +1 3Re ^{000  1}

-

u 0 ^{k + 1}), l = 0,

l = 0, ..., n .

Применяя формулу интегрирования по частям к (22), получим

2 k +1 k +1

-

γ r ² µ ^k 2 h RePr ^{l - 1 l - 1}

-

γ r 2 _µ k ⎞ e 2 h RePr ^ll ⎠ ^l

k +1 l -1 ⁺

¹ ⎛ ∂∂ u ∂ϕ γ ∂ e ∂ϕ ⎜ r ² ϕ _l ( ρ e ) + 2 r ϕ _l uP + r ² ϕ _l P - r ² u ρ e ^l +        r ² µ      ^l

₀ ⎝     ∂ t ∂ r ∂ r Re Pr ∂ r ∂ r

-

h

τ

2 h RePr

γ r 2 _µ k ₊γ r 2 _µ k ⎞ e k + 1 ₊ h RePr ^{l l} 2 h RePr ^{l + 1 l + 1 ⎟}⎠ ^l

4₂     ⎛∂ u ⎞ ² 4 ∂ u ⎞

-      r ² ϕ _l µ⎜     ⎟+ r ϕ _l µ u ⎟ dr + ( u ρ e ϕ _l )

3Re       ⎝∂ r ⎠ 3 Re        ∂ r ⎠

- r=1

+

-

γ r ² µ ^k + r ² u ^{k + 1} ρ ^{k + 1} +    γ r ² µ ^k

2 h RePr ll 2 l + 1 l + 1 l + 1 2 h RePr l + 1 l + 1

k + 1 ⎟ ^el + 1

γ∂ e ⎞ ϕ l µ⎟ Re Pr     ∂ r ⎠ ^{r = 1}

= 0, l = 0, ..., n .

h

= r_l ² ρ _l ^k e_l ^k τ

-

2 hr l u l^{k + 1} P l - 2 r l ² P l^k ( u l^k +^{+ 1}

-

_ul k _-+ ₁ 1_{) +}

Подставим в равенство (23) вместо e приближенное решение (21):

n ⎛1⎛∂∂ϕ γ∂ϕ ∂ϕ ⎞ ∑⎜ ⎜r2ϕlϕi (ρei)-r2uρ leiϕi+      µr2ei il⎟dr+ i=0 ⎝0⎝∂t∂rRePr       ∂r∂r⎠

3 h Re

r l ² µ l^k ( u l^k +^{+ 1}

-

k +12

-

3Re

kk +1 k +1 k +1 r l ^µ l u l ( u l +1 ^- u l -1 ),

l = 1, ..., n - 1,

+⎜ u ρϕ _le_i ϕ _i

-

γ      ∂ϕ

µϕ _le_i ⁱ

Re Pr       ∂ r

r =1

=- ⎜ 2 r ϕ _luP + r ² ϕ _lP -

0 ⎝                  ^∂ r

4         ⎛∂ u ⎞     4 ∂ u ⎞

-      r ² ϕ _l µ⎜    ⎟+ r ϕ _l µ u ⎟ dr ,

3Re      ⎝∂ r ⎠ 3 Re       ∂ r ⎠

l = 0, ..., n .

С учетом выбора базисных функций (6) отличными от нуля в (24) остаются следующие слагаемые:

^{l + 1} ⎛ ¹ ⎛       ∂∂ϕ γ∂ϕ ∂ϕ ⎞

∑ ⎜ ⎜ r2ϕlϕi (ρei) -r2uρ leiϕi+      µr2ei ildr+ i=l-1 ⎝0⎝       ∂t∂rRePr       ∂r∂r⎠

+⎜ u ρϕ _le_i ϕ _i

-

γ       ∂ϕ

µϕ _le_i ⁱ

Re Pr       ∂ r

1 ⎛∂

=- ⎜ 2 r ϕ _luP + r ² ϕ _lP -

0⎝

- r ² ϕµ+ 3Re ^{l ⎜}⎝∂ r ⎠

3Re

∂u ⎞ r ф;ц u     dr, 1 = 0, ..., и l ∂r ⎠

Для вычисления интегралов в уравнении (25) применим квадратурную формулу трапеций и равенства e -1 = e ₀, ц _{- 1} = ц ₀, вытекающие из симметрии задачи. Аппроксимируя производную по времени правой разностной производной, в итоге получим разностные уравнения:

h r 2 ρ k +1 ₊    3 γ r 2 _µ k ₊     γ

τ ⁰⁰   2 h RePr⁰⁰ 2 h RePr

2 k ⎞

_{⎟ e 0} k +1 ₊

2 k +1 k +1 n -1 u n -1 ρ n -1

-

γ

2 h RePr

r n -1 ^µ n -1

-

γ

2 h RePr

⎞ _rn 2 _µ k _{n ⎟}

k +1 ⎟ e n -1 ⁺

h _rn 2 _{ρ n}k + 1 ₊      γ      _rn 2 _{- 1 µ} k_{n - 1 +} 1 _rn 2 _unk + 1 _ρ k_n + 1

2 τ        2 h Re Pr        2

h 2 kk

= r ² ρ ^k e ^k n ρ nn

2 τ nnn

-

hr u ^{k + 1} P ^k nn n

-

3 h Re

-

γ     _r 2 _µ k ⎞ _ek + 1

2 h RePr ⁿⁿ ⎠ ⁿ

1 r 2 P k ( u k +1

2 nn n

_rn 2 _µ k _{n ( un} k +1

-

_un k _-+ ₁ 1₎2

-

-

k +1 u_n k _-+ ₁ 1 ) ₊

2       kk +1 k +1

- r_n µ _nu_n ( u_n 3Re

-

u n^k -⁺1 ¹), l = n .

⎛ γ 2 k 1 2 k +1 k +1 γ

+-       r µ+ ru ρ +

^⎜⎝ 2 h RePr⁰⁰ 2^{11 1}   2 h RePr

2 k ⎞

_{⎟ e 1} k +1

h

= r ₀ ² ρ ^k ₀ e ₀ ^k τ

-

2 hr 0 u 0 ^{k + 1} P 0 ^k - 12 r 0 ² P 0 ^k ( u 1 ^{k + 1}

-

k +1 u ₀) +

3 h Re

r ₀ 2 _{µ 0} k ( u ₁ k +1

-

_{u 0} k +1₎2

-

Таким образом, получена консервативная вариационно-разностная схема первого порядка аппроксимации. К решению получаемых больших систем линейных алгебраических уравнений специального вида с трехдиагональной матрицей применяется метод немонотонной прогонки с итерациями, который отличается высокой вычислительной устойчивостью.

Полученный программный продукт реализован на вычислительной системе в виде тестовых расчетов. В качестве начальных условий использовались значения плотности, динамического коэффициента вязкости, давления и температуры (см. таблицу). В расчетах плотность и динамический коэффициент вязкости, а также температура отнесены к соответствующим характерным величинам на поверхности земного шара.

Представим результаты вычислительного эксперимента в виде графиков (рис. 2, 3). Эти графики показывают, что со временем наша планета сжимается под действием гравитационных сил и уменьшается в радиусе, плотность Земли возрастает во всех слоях, но основные геодинами-ческие зоны сохраняются, хотя и становятся более сглаженными. В свою очередь с увеличением плотности в центре земного шара возрастает давление, направленное в противоположном внутренним гравитационным силам направлении, что приводит к расширению вещества Земли и увеличению ее радиуса. Поверхность Земли определяется значением переменной r, при котором значение безразмерной плотности равно единице.

Таким образом, в данной статье внутреннее строение Земли впервые представлено в рамках газодинамической модели. В результате решения поставленной задачи рассмотрены сферически-симметричные пульсации Земли под действием гравитационных сил с учетом конвекции и диффузии глубинных слоев как сплошной среды.

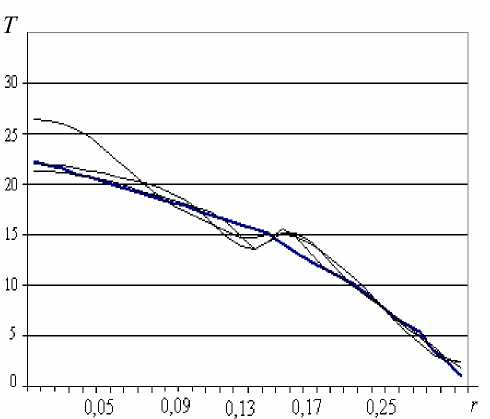
Рис. 2. Распределение плотности по радиусу Земли для различных моментов времени под действием гравитационных сил (выделена линия начального распределения плотности, соответствующая важнейшим граничным поверхностям Мохоровичича и Вихерта-Гутенберга)