Генерации тепловой энергии в шлаковой ванне при электрошлаковом переплаве: математическое моделирование
Автор: Потапов В.И., Суров А.Н., Игизьянова Н.А., Рябинин Т.В.
Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy
Статья в выпуске: 24 (124), 2008 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/147156587
IDR: 147156587 | УДК: 681.32
Текст статьи Генерации тепловой энергии в шлаковой ванне при электрошлаковом переплаве: математическое моделирование
При электрошлаковом наплавлении сплошных или полых слитков большого диаметра появляется неоднородность температурного поля в шлаковой ванне. Эта неоднородность особенно существенна при наплавлении полых слитков большого диаметра. Если при наплавлении сплошных слитков шлаковая ванна достаточно компактна по объему и конвективные потоки относительно выравнивают температурное поле, тогда как при наплавлении полых слитков этого не происходит. Хотя результаты экспериментальных исследований температуры шлаковой ванны при переплаве в круглом кристаллизаторе при однофазной схеме включения расходуемого электрода показывают, что максимальная температура жидкого шлака наблюдается под электродом, при этом перепады температуры по высоте и диаметру шлаковой ванны достигают 100... 150°C [1]. Об этом свидетельствуют так же данные рентгеновского просвечивания шлаковой ванны [2], в результате которого обнаружено, что зона максимальных температур, определенная по интенсивности засвечивания пленки, находится в межэлектродном промежутке.
При наплавлении полых слитков (трубных заготовок) большого диаметра шлаковая ванна заполняет коаксиальное пространство между внешней и внутренней стенками. Восемь расходуемых электродов включены по бифилярной схеме (рис. 1).
Расстояние между электродами А, В назовем межэлектродным промежутком. Шлаковая ванна при этом представляет собой часть коаксиального канала прямоугольного или более сложного сечения (рис. 2, б). Электрический ток протекает между электродами А и В. При этом боковые стенки канала керамические, а частью дна канала является жидкометаллическая ванна. При однофазном включении электрода шлаковая ванна в виде цилиндра (рис. 2, а). Формирование температурного поля в таком канале происходит вследствие выделения энергии при прохождении электрического тока в жидком проводнике - шлаковой ванне с большим сопротивлением. В результате происходит нагрев его до высокой температуры. В меж-
б)
Рис. 2. Схема дискретизации пространства шлаковой ванны: а - при однофазном включении цепи; б - при бифилярном
электродном промежутке канала выделение энергии будет распределенное, так как распределенной будет сила тока. Если пренебречь теплообменом стенок канала с окружающими средами (стенками кристаллизатора, зеркалом жидкометаллической ванны, воздухом), то распределенное выделение энергии по длине канала и определит температурное поле. Можно утверждать, что каждой точке шлакового пространства будет соответствовать точечный источник энергии. Неоднородность температурного поля приводит к неравномерности оплавления торца расходуемого электрода, неравномерности теплообмена с окружающими средами. Поэтому изучение анизотропности температурного поля в шлаковом пространстве представляет как научный, так и практический интерес.
В данной работе рассматривается оценка анизотропии энергетического поля в шлаковом пространстве при ЭШП. При этом исходили из следующих допущений: так как при ЭШП энергия для переплава генерируется в шлаковой ванне электрическим током, то за основу были взяты фундаментальные законы электромагнитной динамики; теплообмен шлаковой ванны с окружающими средами, который искажает температурное поле, создаваемое источниками энергии, рассмотрен отдельно [5] и в данном случае не учитывается; теплообмен между каплями жидкого металла, стекающими с торца расходуемого электрода, и шлаком незначителен по сравнению с общей энергетикой процесса; процесс электродинамический считается осесимметричным, установившимся.
Исходя из принятых допущений за основу были взяты уравнения Максвелла, адаптированные для данного процесса [3, 4]. Уравнения, описы вающие электромагнитные процессы в электроде, шлаковой ванне, имеют вид:
Поле потенциала в шлаковой ванне описыва ется уравнением Лапласа а2 и 1 аи э2и dr2 г 8r dz2
Граничные условия имеют вид:
в области входа электрода в шлаковую ванну
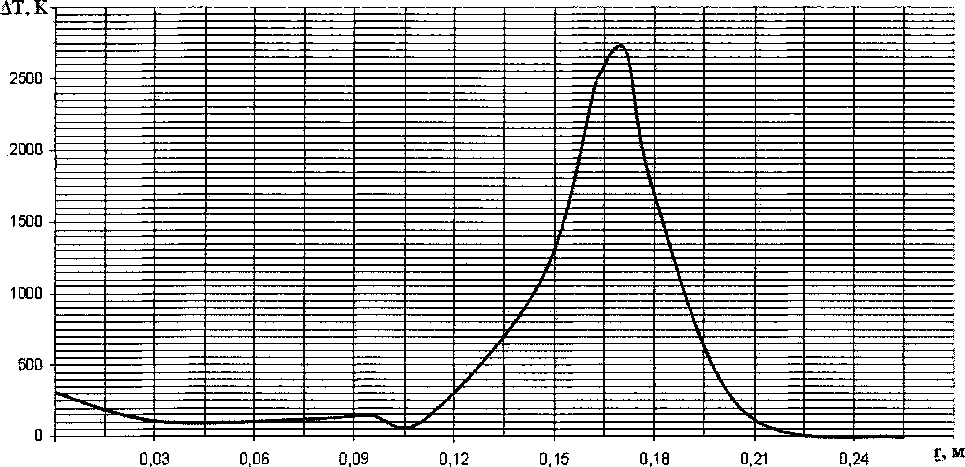
V,z: 0 8z о в области свободной поверхности шлаковой ванны {r,z:r 8z в области дна шлаковой ванны {r,z:0 (r,z:r 3az на боковой поверхности шлаковой ванны {r,z: r = 0, c 8г {r,z: r = R, c 8n Напряженность электрического поля Е определяется из уравнений - - аи - аи Е — —v с/, Е —---, Ег —--» Эп 8г е<р=-др \ЕНЕг+Е>Е"- Плотность электрического тока в шлаковой ванне вычисляется из соотношения, приведенного в [3] 1 = <тЕ. (7) В уравнениях (1)—(7) приняты обозначения: U - потенциал, В; г, z — координаты точек пространства шлаковой ванны, м; j3 - плотность тока на пятне электрода, кА/м2; <т - удельная проводимость шлака, (Ом м) 1; c,d- координаты границ шлаковой ванны; п - нормаль боковой поверхности ванны. По известному вектору плотности электрического тока в каждой точке шлакового пространства вычисляется сила тока Интегрирование распространяется на все поперечное сечение 5 проводника (шлака). Плотность постоянного тока одинакова по всему сечению s проводника. Поэтому для постоянного тока I = js. Решение уравнений (1)—(7) проводилось численным методом конечных разностей. Заменили частные производные в уравнениях (1)—(7) приближенными разностными производными в направлении переменных z, г, получили разностные уравнения. Схема дискретизации пространства шлаковой ванны в однофазной и бифилярной схемах включения печи ЭШП приведена на рис. 2. Был использован шаблон разностного уравнения по явной схеме. Для вычисления значения разностного решения на (z + 1)-m слое используются значения искомого решения на двух предыдущих слоях z-м и (z-I)-m. При этом при z = 0 и z = l используются граничные условия (2)-(5). В качестве сетки при дискретизации шлакового пространства Д принята совокупность прямых г = ut\r,z = mh, где и = 1,2,..., к; т = 0,1,2,...,/; Аг > 0; h > 0. Производные в уравнениях (1)-(6) заменили разностными аналогами вида: Ur = (2Ar)-1 [(/ (mh, (и + l)Ar) - U (mh, (и - l)Ar]; Urr = Ar ~2 [t7 (mh, (u +1) Ar) - 2U (mh, u/V) + + U (mh, (u - l)Ar)J; U. = (2hy\U(m + Y)h,uEr)-U((m-l)h,iikr)y, U„ = h-2 [[Z ((m + Y)h, и Ar) -2U (mh, и Ar) + + U ((m — l)h, мАг)]. При такой дискретизации шлакового пространства Д шаг по г определяет цилиндр радиуса г,, а шаг по z - слой высотой h. Для упрощения вычислительной схемы расчета приняли, шлаковую, ванну при бифилярном включении электродов в виде сектора тора. После дискретизации уравнений (1)—(6) была получена система алгебраических уравнений относительно неизвестных значений функций в узлах сетки, которая решалась на компьютере. В результате компьютерного моделирования были получены значения в узлах сетки: потенциала U , плотности тока j, силы тока I, энергии Q, выделяемой в шлаке током I, разность температур М. На рис. 3 приведены изолинии плотности тока в сечении шлаковой ванны. Расчетные данные показывают, что плотность тока в точках шлаковой ванны распределяется неравномерно: от значений равных нулю - изолинии под номером 0 и до 10 618 кА/м2 на зеркале жидкометаллической ванны. Наибольшая плотность тока наблюдается при радиусе г = гэ, гэ - радиус расходуемого электрода. Под электродом плотность тока более равномерная и при гэ<г<гк при z = mjh, (/ = 5,10) плотность тока нулевая, где гк - радиус кристаллизатора. В этой части пространства не наблюдается и выделение энергии, эта область есть самое холодное пространство шлаковой ванны. Конечно, в действительности происходит некоторое выравнивание выделенной энергии конвективными потоками жидкого шлака, теплопроводностью. По найденным значениям плотности и силы тока определялась выделенная энергия в точках шлакового пространства по известному феноменологическому соотношению Q = I2^ т. е. рассчитывались элементы энергетической матрицы (MfyL i = V2,...,k, j = 0,l,2,...,m, где qy -это величина энергии, Дж, в узлах сетки с номерами М • Исходя из принятого допущения, что внешний теплообмен шлаковой ванны отсутствует, тогда внутри ванны распределение тепла происходит теплопроводностью. Из соотношения для теплового потока Т —Т Аг от слоя к слою была вычислена разность температур 7]+1-7]=А7). Теплопроводность шлака Ди =4,64Вт/(м К) гэ = 0,15м, гк = 0,26м. Площадь поперечного сечения /-го слоя вычислялась по формуле: 5, = П(г1+А + г, )Аг . Шаг по г был принят равным 0,015 м, а по высоте ванны h = 0,005 м. Соотношение между шагами Аг, А удовлетворяет условию, при котором разностная схема устойчива, для гиперболического уравнения (1) и уравнений (2)-(7). По формуле (8) была вычислена матрица температур АТ = [А/,у], / = 1,2,..., к, j = 1,2,..., m. На рис. 4 приведено изменение АТ) при / = 5, т. е. на середине высоты шлаковой ванны. Максимальное значение температуры наблюдается в области при г = г3 ив этой периферийной зоне электрода вы- Рис. 3. Изолинии амплитуды плотности тока в шлаковой ванне: 0 - 0; 1 - 28,3; 2 - 30,5; 3 - 40,0; 4 - 50,0; 5 - 100,0; 6 -150,0; 7 - 200,0; 8 - 300,0; 9 - 500,0; 10 - 2000,0; 11 - 12000,0 кА/м2 Рис. 4. Изменение разности температур между слоями шлаковой ванны на половине ее глубины, по радиусу деляется максимум энергии и происходит перегрев шлака. При внешнем теплообмене этот пик перегрева сглаживается, но анизотропия температурного поля остается очень значительная. Как отмечено в работах [1, 2] замеры температуры проводились путем просвечивания ванны рентгеновским лучом и по степени затемнения пятна луча на пленке определяли температуру. При этом следует заметить, что луч, проходя по диаметру ванны, дает интегральную характеристику затемнения пятна на пленке. Вычисленная среднеинтегральная температура в сечении (см. рис. 4) по формуле: о 17 АТ^^АТ^Дг = 341,1 К rk ,=1 При наличии внешнего теплообмена эта температура будет ниже, и что соответствует экспериментальным данным работ [1,2]. В результате исследований, проведенных в данной работе можно сделать следующие выводы: Получена математическая модель генерации тепловой энергии в шлаковой ванне. Разработана методика расчета температурного поля в шлаковой ванне. Подтверждено предположение о значительной анизотропии энергетического поля в шлаке. Выявлено наличие зоны, где энергия не генерируется и зоны перегрева шлака, на периферии торца расходуемого электрода. Это и приводит к оплавлению электрода в виде конуса. В работе [5] в математических моделях теплофизических процессов при ЭШП источник энер- гии принимался в качестве граничного условия в среде для шлаковой ванны, то при наличии модели полученной в данной работе можно объединить электродинамику и теплофизику при ЭШП в одну математическую модель электрошлакового переплава.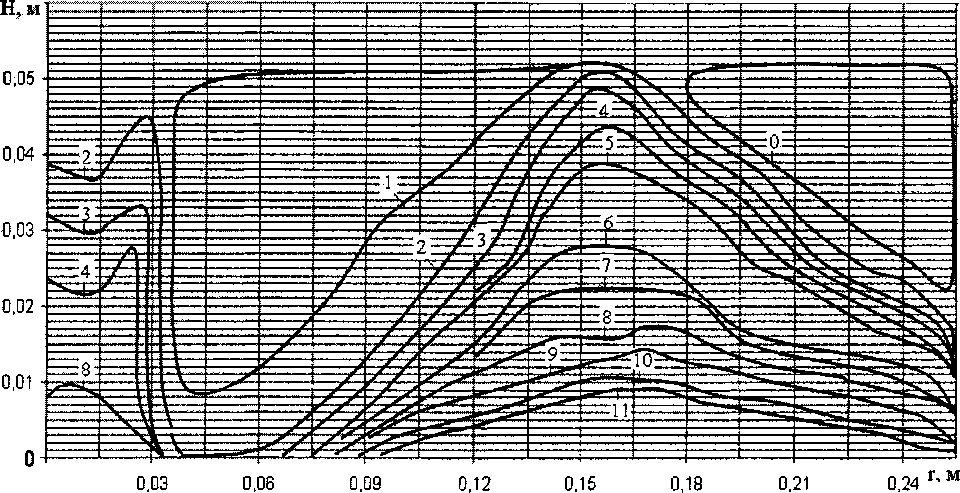
Список литературы Генерации тепловой энергии в шлаковой ванне при электрошлаковом переплаве: математическое моделирование
- Йоши С. Электрошлаковый переплав/С. Йоши, А. Митчел. Киев: Наукова думка, 1973. С. 168-180.
- Панин В.В./В.В. Панин, О.В. Беровский, И.С. Ивахненко//Изв. АН СССР. Металлургия и горное дело. 1963. № 6. С. 90-95.
- Игизьянова Н.А. О расчете электромагнитных процессов при электрошлаковом переплаве/Н.А. Игизьянова, В.И. Потапов//Вестник ЮУрГУ. Серия «Металлургия». 2006. Вып. 7. № 10. С. 76-77.
- Электродинамические процессы при ЭШП на постоянном токе и их математическое моделирование/В.И. Потапов, Н.А. Игизьянова, И.В. Чуманов, Д.А. Пятыгин//Современные проблемы электрометаллургии стали: материалы XIII Междунар. конф.; под ред. В.Е. Рощина. Челябинск: Изд-вo ЮУрГУ, 2007. 4.2. 216 с.
- Суров А.Н. Расчет температурных полей в полых слитках при электрошлаковом переплаве/А.Н. Суров, В.И. Потапов, М.С. Бугаев//Вестник ЮУрГУ. Серия «Металлургия». 2006. Вып. 7. № 10. С. 73-75.


