Генерация бесселевых закрученных пучков в субтерагерцевом диапазоне с использованием отражающих дифракционных оптических элементов

Существование Бесселевых пучков первого рода впервые теоретически было предсказано Дурниным в 1987 г. [1]. Они являются особым несингулярным решением скалярного волнового уравнения Гельмгольца в цилиндрических координатах. Достоинством таких пучков является свойство «бездифракционности» (т.е. сохранение профиля распределения интенсивности поля в поперечном сечении) в свободном пространстве на больших расстояниях, начиная с плоскости их формирования. Ограничения на область распространения связаны с конечностью диаметра освещающего пучка и апертуры элемента, преобразующего входное излучение в Бесселеву моду. Почти сразу Дурнин с соавторами экспериментально продемонстрировали свойства таких пучков в видимом диапазоне длин волн, создавая Бесселевы пучки нулевого порядка с помощью узкой кольцевой щели, помещенной в фокальную плоскость линзы

• [2] . Впоследствии пучки, сохраняющие свой профиль сечения по мере распространения, назвали бездифрак-ционными, одной из наиболее интересных разновидностей которых является Бесселева мода. Исследованию Бесселевых пучков и методов их генерации и детектирования в видимом диапазоне было посвящено много работ [3]. С точки зрения применений, интерес к безди-фракционным пучкам вызван их использованием в системах получения изображений с большой глубиной фокуса [4], микроскопии, для оптической связи [3, 5] и усиления генерации в лазерах на свободных электронах (ЛСЭ) [6].

Бесселевы пучки первого и более высоких порядков обладают орбитальным угловым моментом (ОУМ) которому соответствует определенный топологический заряд моды пучка. Фаза электромагнитного поля в поперечном сечении такого пучка закручена, т.е. меняется в зависимости от азимутального угла и радиального расстояния, а в центре есть не- определенность фазы (сингулярность) [7]. Помимо бездифракционности, закрученные Бесселевы пучки обладают свойством сохранять ОУМ, даже при распространении через амплитудно-фазовые неоднородности, что используется, например, в биомедицинских и телекоммуникационных приложениях [8, 9]. Большой практический интерес закрученные пучки представляют для кодирования информации в квантовых технологиях [10], для манипулирования микрочастицами (так называемые оптические пинцеты) [11], получения изображений, тестирования материалов [12], метрологии и астрономии [13].

Немаловажное значение для приложений закрученные Бесселевы пучки имеют и в терагерцевом (1 – 10 ТГц) и миллиметровом /субтерагерцевом (0,1 – 1 ТГц) спектральных диапазонах для создания изображающих систем и сенсорных устройств [14], неразрушающего тестирования объектов [15]. Ожидается, что использование Бесселевых пучков высоких порядков позволит расширить возможности систем беспроводной связи в окнах прозрачности миллиметрового диапазона длин волн [16]. Детальный обзор работ по теории и применению Бесселевых пучков с ОУМ в видимом и ТГц-диапазонах приведен в работе [17].

В 1999 г. впервые в миллиметровом диапазоне (на частоте 90 ГГц – нижняя граница субтерагерцевого (субТГц) диапазона) был получен Бесселев пучок нулевого порядка при пропускании Гауссового пучка, генерируемого диодом Ганна, через конический фазовый аксикон из прозрачного для данного диапазона полиэтилена [18]. Диаметр центрального пятна Бесселева пучка имел ширину 4 мм, что немного превышало длину волны излучения (3,3 мм). При этом длина бездифракционной области составляла более 70 мм, что намного превышало длину Релея Гауссо-вого пучка (10 мм). Позднее Бесселевы пучки более высокого порядка были сгенерированы с помощью бинарных амплитудных голограмм [19], однако дифракционная эффективность таких элементов была невысока (не более 45 %). Были предложены бинарные фазовые дифракционные оптические элементы (ДОЭ), рассчитанные с помощью стохастической оптимизации в рамках строгой теории, для создания Бесселевых пучков любого порядка с дифракционной эффективностью до 94% [20, 21], однако из-за сложного бинарного рельефа и высокого аспектного отношения его элементов, такие элементы на прозрачном в ТГц диапазоне материале (тефлон) авторам [20, 21] не удалось изготовить. Более простым и реализуемым способом создания бесселевого распределения поля с ОУМ явилось пропускание падающего пучка через плоскопараллельную пластинку из композитного материала с двумерным спиральным распределением эффективной диэлектрической проницаемости, формируемого круглыми субволновыми отверстиями разного диаметра [22]. С помощью данного метода получилось сформировать не только пучки с заданным ОУМ в миллимет- ровом диапазоне, но и пучки с комбинацией нескольких ОУМ, за счет формирования на одной метапластинке нескольких типов распределений проницаемости, соответствующих определенному ОУМ.

С развитием техники 3D-печати стало возможным изготовление металинз, состоящих из ячеек субволнового размера разной толщины. За счет специально заданного распределения толщин таких ячеек на диэлектрической линзе удалось сформировать пучки с разными ОУМ [23]. Используя специальные методы оптимизации распределения таких ячеек в трехмерной структуре линзы, удалось получить Бесселевы пучки с ОУМ, имеющие область бездифракционно-сти, начинающуюся не сразу после линзы, а в заданном отрезке расстояний от нее, что представляет большой интерес для развития субТГц беспроводных систем связи [24]. С помощью металинз, созданных по той же технологии, были сформированы закрученные пучки с топологическим зарядом +1 и –1, а также маски для их демультиплексирования [16].

На основе жидких кристаллов (ЖК), обладающих свойством двойного лучепреломления (от видимого до микроволнового диапазонов), в настоящее время активно разрабатываются устройства управления поляризацией излучения, модовым составом пучка, фильтры и четвертьволновые пластинки. Из-за малых потерь ЖК в субТГц-диапазоне и возможности изменения их оптической плотности механическим, оптическим, тепловым воздействием, а также электрическим полем, на основе ЖК разрабатываются различные субТГц модуляционные устройства [25, 26], в том числе и элементы, преобразующие излучение в Бесселевы пучки с ОУМ [27].

Несмотря на имеющийся опыт создания Бесселевых закрученных пучков в субТГц-диапазоне, разработанные методы [18–23, 27] ограничены небольшими мощностями излучения. Использующиеся диэлектрические материалы, несмотря на слабое поглощение, при достаточно мощных пучках способны деформироваться за счет теплового нагрева. Пучки большой мощности могут генерировать ЛСЭ [28] и гиротроны [29]. Последние могут использоваться в лидарных системах, для передачи информации на большие расстояния в окнах прозрачности субТГц-диапазона, а также имеют множество применений для построения изображающих и сенсорных систем, обработки материалов, спектроскопии [29]. Достаточной механической прочностью и стойкостью к большим плотностям мощности обладают ДОЭ, изготовленные литографическим травлением на подложках из высокоомного кремния или с помощью технологий лазерной абляции на алмазных поликристаллических пленках, прозрачных в ТГц- и миллиметровом диапазонах частот [30]. На основе высокоомного кремния было создано и апробировано множество различных дифракционных элементов для работы с высокой средней мощностью излучения (порядка сотен Ватт), генерируемого Новосибирским ЛСЭ [31 – 33]. Однако при переходе в субТГц-диапазон, где длины волн достигают миллиметров, высота микрорельефа должна составлять сотни микрон, что трудно обеспечить при использовании методов литографии или абляции. Кроме того, кремний и синтетический алмаз обладают высокой оптической плотностью, что приводит к значительным френелевским потерям на отражение. Снизить френелевские потери можно с помощью нанесения на поверхность подложки дифракционного элемента просветляющего покрытия, что усложняет технологию изготовления и снижает лучевую стойкость отражающего элемента [34].

Наиболее подходящими для управления поперечно-модовой структурой мощных субТГц-пучков могут быть отражающие ДОЭ, изготовленные на металлической поверхности (обладающей в субТГц-диапазоне очень низкими тепловыми потерями при отражении [35]), на которой можно создавать достаточно глубокий микрорельеф при использовании простых методов механической обработки [36]. Одним из возможных применений отражающих металлических элементов является создание бездифракционных Бесселевых пучков для повышения эффективности генерации мощного лазерного излучения в вигглерах ЛСЭ [6].

В данной работе элементы для создания закрученных Бесселевых пучков субТГц-диапазона с орбитальным угловым моментом l = 1 создавались микрофрезерованием с помощью ЧПУ на дюралевой полированной подложке либо литьем из олова. Данные элементы были протестированы на излучении лампы обратной волны (длина волны λ =855 мкм). Приведено сравнение экспериментальных данных с результатами численного моделирования.

1.    Изготовление отражающих дифракционных оптических элементов

Для изготовления фазовых спиральных отражающих ДОЭ с непрерывным рельефом было предложено две технологии – фрезерование и литье. Достоинством изготовления фрезерованием является доступность технологии и возможность использования более широкого спектра материалов, пригодных для механической обработки. К недостаткам данного метода можно отнести не очень высокую точность механической обработки поверхности, приводящую к повышенной шероховатости поверхности по сравнению с оптическими методами полировки и может привести к потерям мощности излучения на рассеяние. К преимуществам литья можно отнести сравнительно низкую стоимость единичного элемента и меньшую шероховатость поверхности, а к недостаткам — высокую стоимость оснастки и сравнительно более высокую погрешность формы элемента [37, 38]. Изготовление элемента (№1) методом фрезерования пластины из сплава Д16Т проводилось на микрофре-зерном станке Proxxon MF70 (Германия) с использо- ванием сферической твердосплавной фрезы диаметром 0,8 мм при скорости вращения шпинделя 20000 об/мин и скорости подачи 100 мм /мин. Для создания чистовой траектории использовался собственный генератор G-кода станка, что позволило избежать внесения погрешностей формы, связанных с представлением модели в CAD / CAM-системах [36]. Для изготовления элемента (№2) литьем была отфрезерована литьевая форма Д16Т, в которую производилось литье чистого олова (ЧДА) при температуре 300⁰С. Выбор олова в качестве материала для изготовления элемента обусловлен его относительно низкой температурой плавления и практически 100% (как и Д16Т) коэффициентом отражения в исследуемой области спектра. Температура после отливки снижалась до комнатной в течение 8 часов. После остывания производилась химическая и механическая обработка рабочей поверхности элемента с целью удаления механических примесей и оксидного слоя. Геометрические размеры рабочей поверхности элементов составляли 80 ×70 мм.

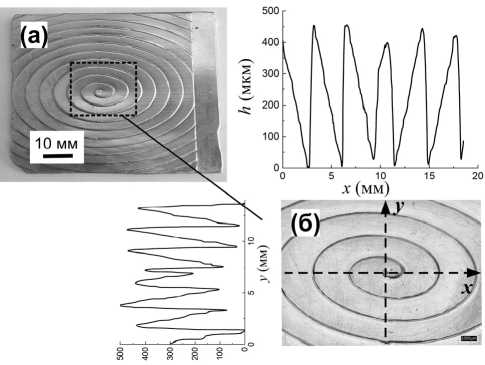
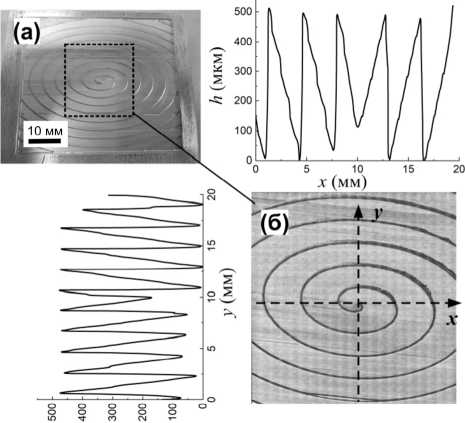
На рис. 1 а и рис. 2 а показаны фотографии отражающих элементов №1 и №2, предназначенных для формирования пучков с орбитальным угловым моментом l =1. На рис. 1 б и рис. 2 б показаны увеличенные изображения центральной части элементов, полученных на конфокальном микроскопе VHX-6000. На профиле сечений виден плавный перепад высот h , что характерно для непрерывного рельефа. Максимальный перепад составляет h ≈ 450±20 мкм и несколько отличалось от расчетного значения высоты рельефа для угла падения освещающего пучка 45 градусов и рабочей длины волны. Периоды обеих дифракционных решеток по вертикали составляют р в =2±0,1 мм (что соответствует углу блеска решетки ≈ 13°), а по горизонтали в 1,7 раза больше р г =3,4±0,1 мм. Далее под периодом решетки мы будем подразумевать вертикальный период и обозначать его p . В центральной области апертуры оптических элементов наблюдаются определенные нарушения периодической структуры решетки, что оказывало влияние на работу элементов.

2.    Численное моделирование

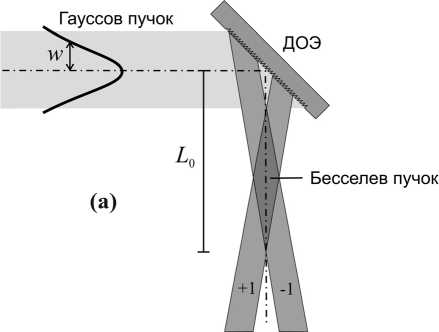
Бесселевы пучки, формируемые ДОЭ, образуются конически сходящимися волнами первого дифракционного порядка в области их перекрытия (рис. 3а). С целью сравнительного анализа разных подходов к формированию ТГц-пучков с ОУМ в настоящей статье результаты экспериментального исследования формирования Бесселева пучка с ОУМ с помощью отражающего элемента (рис. 1–2) сравнивались c результатами численного исследования формирования такого пучка с помощью пропускающего элемента [32]. При этом в моделировании предполагалось, что Бесселев пучок формируется пропускающим фазовым бинарным спиральным аксиконом [32] с параметрами (апертура, период, топологический заряд, длина волны освещающего пучка), соответствующими параметрам изготовленных отражающих элементов. Отметим, что результаты экспериментов по формированию Бесселева пучка с ОУМ с помощью пропускающего фазового бинарного спирального аксикона и исследованию распространения сформированного пучка в свободном пространстве, ранее приведённые в [32], находятся в хорошем соответствии с результатами численного моделирования, выполненного тем же методом, что и в настоящей работе. Расчеты распределения интенсивности поля в сечении сформированных после ДОЭ пучков выполнялись на основе скалярной теории дифракции с помощью специально написанной программы в Matlab [39]. Предполагалось, что элемент освещался плоским Гауссовым пучком с длиной волны λ =855 мкм и радиусом перетяжки w =22 мм. На рис. 3б представлены распределения интенсивности в сечении пучка в плоскостях, отстоящих от элемента на расстоянии L = 10–70 мм. На рис. 3в показано распределение продольного сечения формируемого пучка. Параметры излучения и ДОЭ в расчетах соответствуют условиям эксперимента (см. параграф 3). Как видно на рис. 3б, пучок формирует Бесселево распределение, характеризующееся максимумами интенсивности в виде концентрических колец, начиная примерно с 20 мм, которое сохраняется вплоть до 40–50 мм, а при L >50 мм Бесселев пучок расходится. В области L =40–60 мм на расчетных распределениях интенсивности наблюдаются диагональные линии и квадраты, наличие которых связано с дифракцией излучения на апертуре оптического элемента, которая выбиралась квадратной в ходе численного моделирования. Согласно теории [40], в нашем случае Бесселев пучок должен «разваливаться» при L0 = w × (p/λ) ≈ 51 мм, что хорошо согласуется с приведенными выше численными расчетами.

h (мкм)

Рис. 2. Изображение отражающего ДОЭ №2: (а) фотография, (б) изображение центрального фрагмента апертуры элемента 20×20 мм2 с горизонтальным и вертикальным профилем сечения, полученное на конфокальном микроскопе VHX-6000

h (мкм)

Рис. 1. Изображение отражающего ДОЭ №1: (а) фотография, (б) изображение центрального фрагмента апертуры элемента 20×20 мм2 с горизонтальным и вертикальным профилем сечения, полученное на конфокальном микроскопе VHX-6000

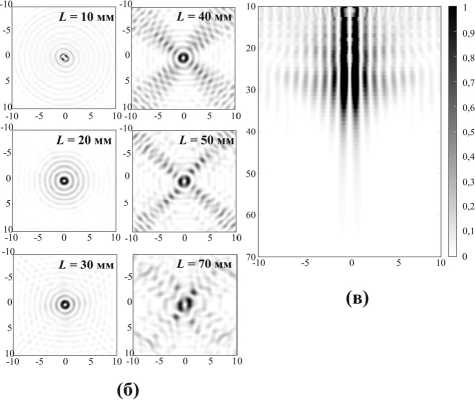
Рис. 3. (а) Схема формирования Бесселева пучка с помощью отражающего ДОЭ; (б) расчетные распределения интенсивности Гауссова пучка с длиной волны λ = 855 мкм и радиусом перетяжки w = 22 мм, формируемые аксиконом с периодом решетки p = 2 мм в плоскостях, отстоящих от элемента на расстоянии L = 10 – 70 мм; (в) распределение продольного сечения формируемого пучка

3.    Эксперимент

В эксперименте в качестве источника излучения использовалась лампа обратной волны (ЛОВ) (производитель ИОФ РАН, Россия) [41], генерирующая непрерывное линейно поляризованное (99,99%) субТГц-излучение, перестраиваемое в диапазоне 0,06–1,5 ТГц (при использовании нескольких типов ламп) и имеющее ширину линии 10 –5 от длины волны λ. Измерения проводились на частоте 0,351 ТГц (λ = 855 мкм), соответствующей максимуму спектральной яркости лампы. Средняя мощность на данной частоте составляла около 40 мВт.

Оптическая схема эксперимента представлена на рис. 4. Излучение ЛОВ собиралось и коллимировалось полиэтиленовой линзой ( Л ), а затем, пройдя через диафрагму ( Д ) диаметром 45 мм, отражалось от металлического зеркала или отражающего ДОЭ. Профиль интенсивности отраженного пучка сканировался однопиксельным пироэлектрическим приемником с размером апертуры 2 мм. Шаг сканирования составлял 0,4 мм, который определял размер пикселя получаемых изображений.

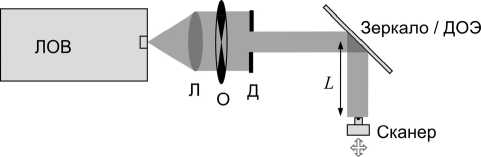
Рис. 4. Оптическая схема эксперимента: Л – полиэтиленовая коллимирующая линза, О – обтюратор, Д – диафрагма (40 мм)

Поскольку пироэлектрический детектор может регистрировать только переменный поток мощности, перед диафрагмой помещался механический обтюратор ( О ), модулирующий интенсивность излучения с частотой 10 Гц.

На рис. 5 показано сканированное изображение сечения пучка, отраженного от зеркала. Пучок имеет характерный Гауссов профиль с радиусом перетяжки w =22 мм. В случае, когда на место зеркала устанавливали отражающий ДОЭ №1 (изготовленный методом микрофрезерования), то в отраженном пучке на расстоянии L =20–70 мм от ДОЭ формировались распределения интенсивности, представленные на рис. 6. Видно, что при L =20–50 мм изображения пучка имеют характерную осесимметричную кольцевую структуру с максимальной яркостью в первом кольце диаметром ≈ 3 мм. Эти результаты хорошо согласуются с результатами численных расчетов (рис. 3), несмотря на то что расчеты выполнялись для бинарного микрорельефа с аналогичными параметрами. При L >50 мм пучок расходится, и профиль интенсивности перестает аппроксимироваться функцией Бесселя. Провести измерения на меньших расстояниях L <20 мм, чтобы увидеть область, где пучок еще не был сформирован, не было возможным из-за ограничений габаритных размеров детектирующей головки однопиксельного приемника.

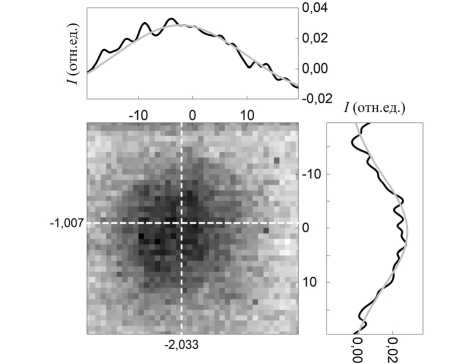
Рис. 5. Изображение поперечного сечения пучка, отраженного от зеркала, полученное на расстоянии 80 мм от него. Область сканирования – 40×40 мм2, шаг сканирования – 1 мм. Серыми линиями показаны графики Гауссовой аппроксимации горизонтального и вертикального профилей сечения пучка

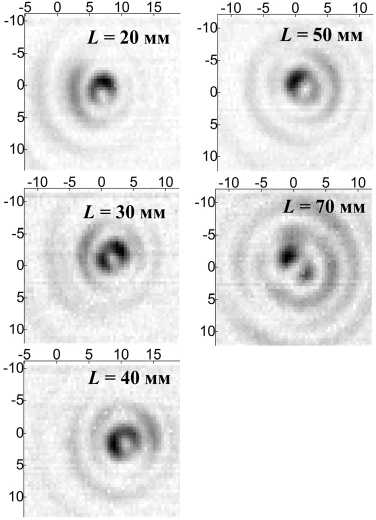
Рис. 6. Изображения поперечного сечения пучка, отраженного от ДОЭ №1 (изготовленного методом микрофрезерования), полученные на расстояниях L = 20 – 70 мм. Область сканирования – 24×24 мм2, шаг сканирования – 0,44 мм

Энергетическую эффективность Ef дифракционного оптического элемента (которая в общем случае учитывает и его дифракционную эффективность, и возможные потери на рассеяние, поглощение и френелевское отражение (в случае элемента на пропускание)) можно оценить, как отношение суммарной интенсивности сформированного Бесселева пучка Iб к интенсивности излучения I0, падающего на элемент. Интенсивность Бесселева пучка в области формирования (L =30–40 мм) находилась суммированием сигнала по всему кадру (см. рис. 6) и составила Iб ≈ 13 отн. ед. Интенсивность падающего пучка вычислялась суммированием сигнала по площади сечения Гауссова пучка и составила I0 ≈ 20 отн. ед. Таким образом, экспериментальная оценка энергетической эффективности отражающего элемента составила Ef ≈ 63 %. Понижение дифракционной эффективности вызвано в основном наличием расходящихся волн первого порядка дифракции, не участвующих в формировании Бесселева пучка [42], а также потерями из-за разницы интенсивности освещающего и формируемого пучка, из-за рассеяния на неоднородностях микрорельефа и технологических погрешностей. Отметим, что энергетическая эффективность кремниевого дифракционного элемента на пропускание ограничена сверху величиной в 50 % из-за потерь на френелевское отражение (без учета других источников потерь, о которых говорилось выше).

На рис. 7 представлены экспериментальные результаты для элемента №2, изготовленного методом литья. Видно, что в области L =20–50 мм, где, согласно расчетам, должен формироваться Бесселев пучок, профиль распределения интенсивности заметно искажен. В дополнительных экспериментах с данным элементом было обнаружено, что искажение профиля связано с неплоскостностью подложки элемента, возникшей вследствие малых остаточных деформаций олова, обладающего пластичностью. При работе на отражение такие деформации существенно искажают профиль формируемого пучка.

Рис. 7. Изображения поперечного сечения пучка, отраженного от ДОЭ №2, полученные на расстояниях L = 20 – 70 мм. Область сканирования – 24×24 мм2, шаг сканирования – 0,56 мм

Заключение

В работе предложен простой способ создания закрученных Бесселевых пучков субТГц-диапазона с орбитальным угловым моментом l = 1 с помощью отражающих металлических дифракционных оптических элементов с непрерывным профилем микрорельефа. Микрорельеф отражающих элементов создавался 1) микрофрезерованием поверхности дюралевой полированной подложки или 2) литьем из олова. Созданные элементы были исследованы в субТГц-диапазоне в пучке излучения лампы обратной волны (длина волны λ =855 мкм).

Для элемента, изготовленного микрофрезерованием, пучки формировались и сохраняли Бесселев профиль интенсивности на расстоянии от отражающего элемента 20–50 мм, что хорошо согласуется с результатами численного моделирования и теоретическими оценками. Экспериментально полученная оценка энергетической эффективности элемента составила 63%.

Для элемента, изготовленного методом литья из олова, формируемые пучки имели искажения профиля вследствие наличия остаточных деформаций олова, обладающего пластичностью. Для минимизации деформаций необходимо подбирать литейные материалы и термические режимы их обработки при изготовлении элемента.

Благодаря высокой отражающей способности металлических отражающих элементов они могут использоваться и при работе с источниками субТГц-излучения с высокой плотностью мощности, таких как лазеры на свободных электронах и гиротроны.

В работе использовалось оборудование Центра коллективного пользования «Сибирский центр синхротронного и терагерцевого излучения» на базе уникальной установки «Новосибирский ЛСЭ» в ИЯФ СО РАН. Авторы благодарят ЦКП ВТАН НГУ за проведение измерений на научном оборудовании. Расчет дифракционных оптических элементов выполнен при поддержке Государственного задания НИЦ «Курчатовский институт».