Генерация и эволюция вогнутых дислокационных петель в процессе распространения элементарного кристаллографического скольжения

Понимание природы пластичности кристаллов и, на его основе, адекватное формальное описание механического поведения кристаллических твердых тел возможно лишь через определенный про межуточный этап синтеза знаний об атомно-лислокационных микромеханизмах пластичности на уровне элемента дислокационной дефектно!! структуры, достаточно большою, чтобы он уже обладал фундаментальными свойствами дислокационной подсистемы кристалла. Если известны свойства мини-малънего представительного структурного элемента и основные взаимодействия таких элементов, дальнейшее построение теории макроскопического пластического поведения кристаллов становится задачей механики деформируемого твердого тела.

Конечно же, выбор минимального представительного структурного элемента не однозначен. Естественным минимальным объектом, отражающим свойства дислокационной подсистемы, является цис локационная петля, отделяющая область, где произошло скольжение от остальной части плоскости кристаллографического скольжения Именно планарная замкнутая дислокация, а не прямолинейная или квазипрямоли-нейная бесконечная дислокация Последние не офажаюг всех фундаментальных свойств дислокационной подсистемы, например, ее способности размножаться в ре-зуд ь гаге многочисленных неу стийчнвостей.

Столь же естественен мезоскопический уровень рассмотрения явления сдвиговой пластичности кристаллов - элементарное кристаллографическое скольжение В процессе распространения элементарного скольжения ограничивающая его расши-ржошаяся замкнутая дислокация пересекает множество дислокаций других систем скольжения - препятствий. При контактном взаимодействии дислокаций возникают либо дефекты дислокации: пороги и перегибы, либо дислокации вступают между собой в дислокационные реакции продуктом которых являются дислокационные соединения Контактные силы, связанные с образованием порогов и перегибов, невелики. В случае же взаимодействия реагирующих .дислокаций происходят значительные изменения протяженности дислокаций и их линейной энергии. Хотя реагирующие дислокации составляют относительно небольшую часть всех дислокаций, пересекаемых замкнутой дислокацией, связанной с кристаллографическим скольжением, при распространении скольжения, они создают основную часть сопротивления движению скользящей дислокации. Силы, необходимые дня взаимного пересечения реагирующих дислокаций, определяются равновесием линейных натяжений в тройных узлах. Величина этих сил может быть весьма различной (or нуля до величин, несколько превышающих силу линейного натяжения). То есть, фактор, сохраняющий конфигурацию дислокации, соответствующую минимуму ее конфигурационной энергии, и фактор, нарушающий эту' конфигурацию, приблизительно одинаковы по величине характеризующих эти взаимодействия сил. По этой причине контуры распространяющегося элементарного скольжения приобретают очень сложную конфигурацию. Кроме того, дислокации некомпланарных систем, пересекающих плоскость скольжения, ориентированы и распределены в пространстве случайным образом. Существуют, следовательно, сгущения дислокационных препятствий высокой прочности, которые могут оказаться непреодолимыми для скользящей дислокации. Это еще более усложняет конфигурацию скользящей дислокации и, в конечном счете, приводит к тому, что в настоящее время распространение элементарного скольжения не удается проанализировать традиционными аналитическими и экспериментальными методами - детальное количественное описание требует привлечения методов имитационного моделирования.

Модель

Модель и принципы ее алгоритмизации для имитации зарождения и распространения элементарного кристаллографического сдвига в плоскости, содержащей случайно расположенные препятствия с дискретным набором прочностей, описана в [1] Под действием приложенного напряжения дислокационный отрезок, шарнирно закрепленный в двух точках, начинает прогибаться, образуя ряд последовательных конфигураций, каждая из которых однозначно определяется набором углов огибания на «встреченных» препятствиях, набором длин дислокационных сегментов и приложенным напряжением (рис. 1, фрагмент 1). При попадании дислокации в конфигурацию, которую она не может преодолеть с помощью термических флуктуаций или силовым путем при данном напряжении г, увеличивается приложенное напряжение. Минимальнее напряжение, при котором генерируется дислокационная петля, принято за напряжение старта источника т«г. Конфигурацию, стабильную при напряжении тл - Ат (здесь Ат ~-0) и расширяющуюся в надбарьерном режиме до замыкания в дислокационную петлю при напряжении т,г или до границы участка плоскости кристаллографического скольжения, будем называть конфигурацией потери механической устойчивости. Входными параметрами модели являются координаты сегмента-источника или точки закрепления дислокационной петли, относительные концентрации и прочности препятствий, условия деформирования, деформируемый кристалл. Реализации экспериментов дают на выходе дислокационные траектории и их характеристики с любой степенью детальности

В данной работе приводятся результаты верификации модели применительно к монокристаллам меди, ориентированным для одиночного скольжения в плоскости <1I1~> в направлении [110] с плотностью дислокаций леса 108 см"2. Препятствия интерпретируются как точки пересечения дислокаций некомпланарных систем скольжения с плоскостью залегания источника; их относительные концентрации с,- и прочности, выраженные в терминах критических углов огибания <р ,, /—1,. .,5, оценены в [2, 3]. Стопоры естественным образом делятся на сильные и слабые (реагирующий и нереагирующий лес) из-за существенного различия как в уровне напряжений, необходимых для их преодоления, так и в возможных механизмах преодоления. В зависимости от типа дислокационных реакций сильные стопоры разделены на 4 типа. Предполагается, что с помощью термических активаций могут быть пройдены только слабые стопоры

Результаты моделирования

Рис 1. отражает типичные события, наблюдаемые в ЭВМ-экспериментах (в представленном случае длина сегмента-источника 19.шеи).

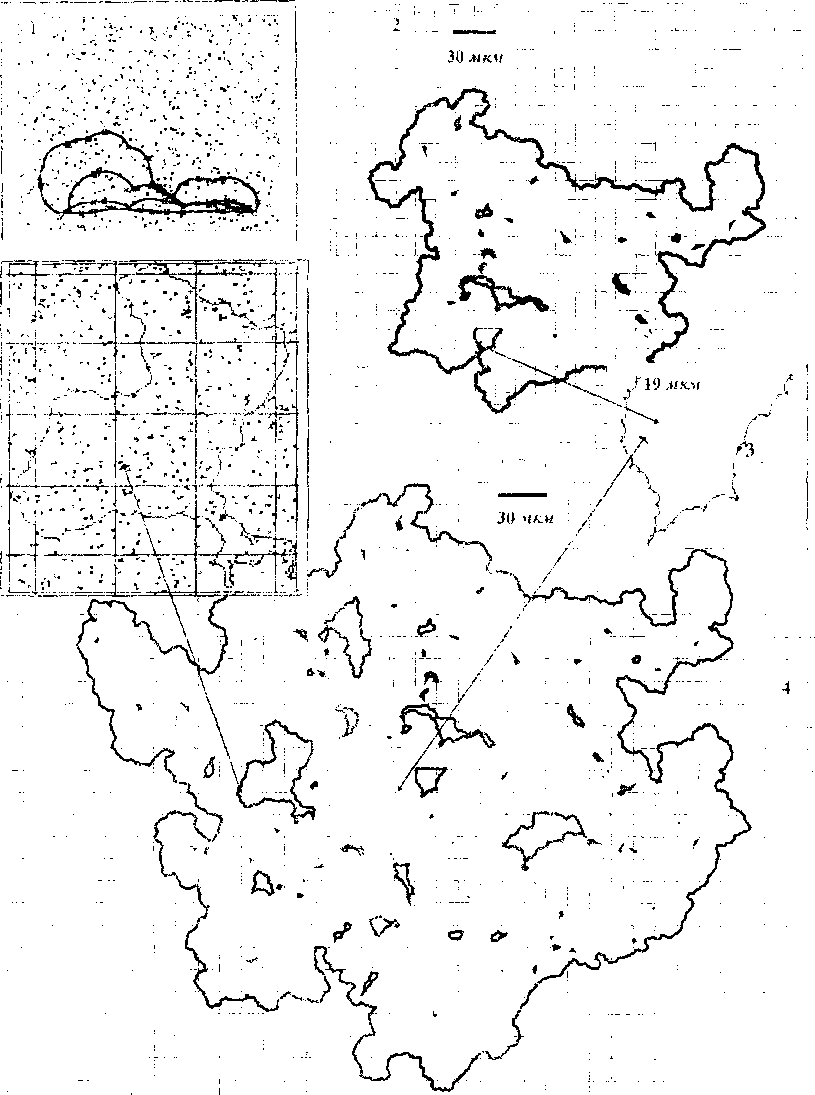
Рис. 1. Эмиссия дислокационной петли источником Франка Рида длины 19 мкм в плоскости залегания которого содержатся случайно расположенные препятствия с дискретным спектром прочностей (ЭВМ-эксперимент 19(3». Препятствия, за исключением 1 и 5 фрагым тс^ пс показаны я каждом квадрате сетки рисунков их, в среднем,по 225. Ч< ый фрагмент плоскости кристаллографического скольжения и, ,ч 241425 стопоров, пятый - 6778

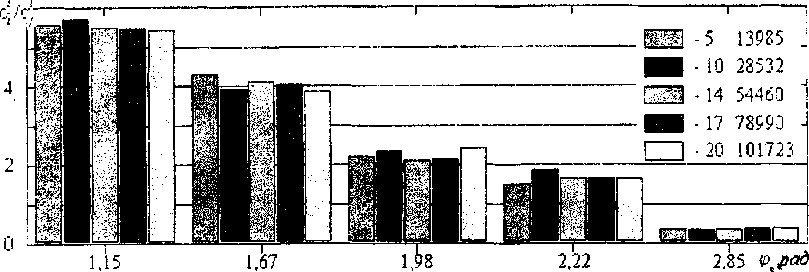
Рис.2. Отношение концентраций стопоров /-го типа вдоль дислокационной петли (с,') и в плоскости кристаллографического скольжения (с)) для различных дислокационных конфигураций: 5 - после прохождения 13985 стопоров, 10 - 28532, 14 - 54460, 17 - 78990, 20 - 101723 (эксперимент 19(3))

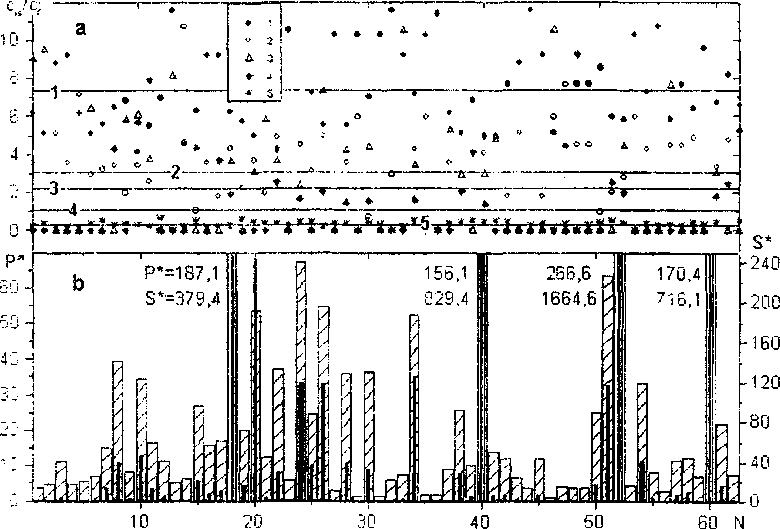
Рис 3. Вероятностно-геометрические характеристики островов незавершенного кристаллографического сдвига для эксперимента 19(3). ?/- порядковый номер острова, Р*, 5*- периметры границы и площади островов, с.) ,с; - концентрации стопоров i - го типа на границах островов и в плоскости кристаллографического скольжения, /=!,...,5, /=] соответствует стопорам с критическим углом огибания 1,15 рад, 2 - 1,67, 3- 1,98, 4 - 2,22,5 - 2,85. Прямые на фрагменте (а) соответствую т средним значениям

Пройдя конфигурацию потери механической устойчивости (последняя на фрагменте I) и ряд промежуточных положений, дислокационная конфигурация «самопересекаетсяя (2) с отделением «хвоста» - начальной конфигурацией источника при его нов горном старте (3) - и замкнутой дислокационной петлей. В отличие от результатов ЭВМ-экспериментов в модели слабых однородных препятствий [4] за фронтом скользящей дислокации остаются дислокационные петельки (вогнутые дислокационные петли - острова незавершенного кристаллографического сдвига), образовавшиеся в результате огибания трудно преодолимых участков плоскости кристаллографического скольжения по механизму Орована.

В представленном эксперименте напряжение старта дислокационного источника т‘₍ =0,2439, что более чем в 4,6 раза превысило напряжение Франка-Рида [5] (верхний индекс (*) здесь и в дальнейшем означает, что помеченные им характеристики дань! в безразмерных единицах линейные - в единицах /_$, напряжения - 2ц / bl,. площади -/‘ (здесь ц - линейное натяжение дислокации, b - модуль вектора Бюргерса, 1 = 1/у о , р - плотность дислокаций леса)). На дислокационной петле, осуществляющей распространение кристаллографического сдвига, после преодоления ею примерно 10000 препятствий, стабилизируются огносительные концентрации стопоров по типам (рис.21 При этом, чем прочнее препятствия, тем больше их концентрация вдоль дислокации. Доля самых прочных препятствий (с критическим углом огибания q\."-=l,15 рад} на дислокации превышает их долю в плоскости кристаллографического скольжения примерно в 6 раз (см. рис 2) Доля же слабых препятствий падает. К моменту выхода лислокационной петли на границу площадки моделирования суммарная площадь 113 островов незавершенного кристаллографического сдвига составила 4829/( (4.6% с; площади ограниченной дислокационной петлей) с периметром 1812/_$ (71.4% от периметра дислокационной негли). Для границ островов незавершенного кристаллографического сдвига (замкнутых вогнутых дислокационных петель) отношения с',, i с ,- еще больше, чем для дислокационной петли применительно к сильным стопорам и меньше для слабых препятствий (см. рис.За); здесь ж., ей- относительные концентрации стопоров /-го типа, соответственно, на вогнутой летле и в плоскости кристаллографического скольжения. Велик разброс в размерах островов: вогнутые дислокационные петли окружают (руп.пы от 3 препятствий до неш-ольких тысяч (см. рис.ЗЬ). К примеру, остров на фрагменте 5 рис.1 содержит более 1600 стопоров. С распространением элементарного кристаллограф-жеского скольжении растет как доля площади островов q₄ в площади, заметаемой дислокационной петлей, так и доля суммарного периметра q. вогнутых петель в цлине расширяющейся петли.

Анализ [6] показал, что острова .незавершенного кристаллографического сдвига представляют собой «сгустки», кластеры» препятствий, локальная плотность которых превышает (за счет сильных препятствий) ее среднее значение в плоскости залегания дислокационного источника, либо среднее расстояние между препятствиями вдоль границы острова меньше среднего расстояния между ближайшими стопорами в плоскости кристаллографического скольжения.

В качественном отношении описанная картина сохраняется и для всех исследуемых длин дислокационных источников (Z е [2,20]) Но число образовавшихся ост -ровов очень чувствительно к напряжению старта дислокационного источника т„ На рис.4 представлены результаты имитации эмиссии дислокационной петли сегментом-источником длиной Zwow. Напряжение старта г‘, в этом эксперименте составило

0.7145.

		15 мкм	\zx	Г		г	г ?
						ш
				u L <к?¥ . С
		15ч		р	£4	R	S'iA.4^
						- ' e^vS	■ ^ '"У "г		3
		L=2 мкл				^1/

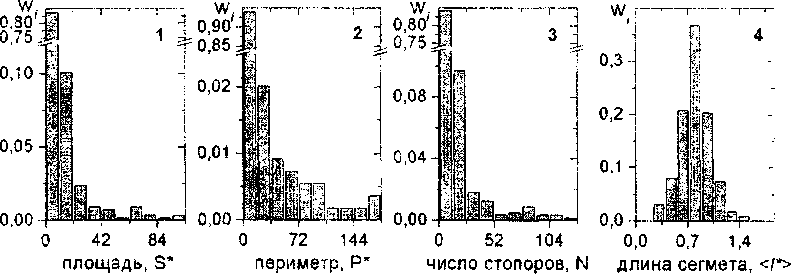
Рис.4 Дислокационная конфигурация от источника длиной 2 мкм после преодоления 11166 стопоров (верхняя часть) и распределения площадей S^x периметров Р*, числа стопоров /V, контактирующих с вогнутыми дислокационными петлями и *> - среднего расстояния между стопорами вдоль вогнутых петель. Все гистограммы построены по 1590 замерам

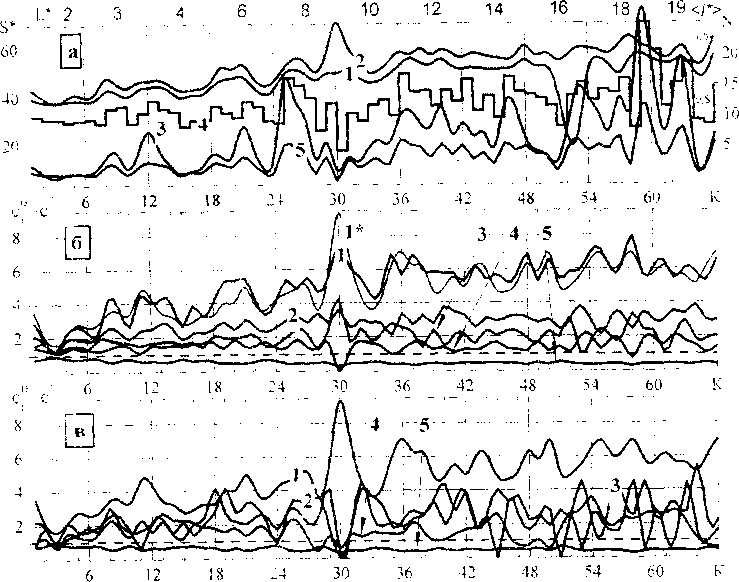
Рис.5 Вероятностно-геометрические характеристики островов

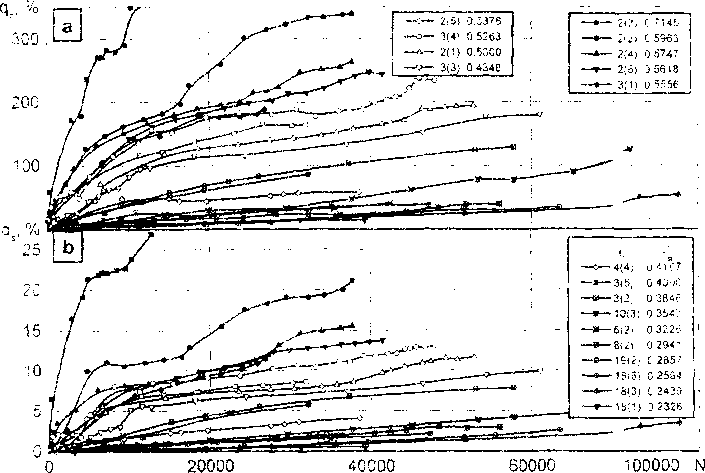
Рис.6. Изменение доля периметра вогнутых петель ( ) в периметре петли и доли их площади с числом пройденных препятствий (N). В легендах кривых: первое число - длина источника в мкм, второе (в скобках) - номер эксперимента для этой длины источника, третье - безразмерное атермическое напрягкение старта источника т*_я

Даже на таком сравнительно малом участке плоскости кристаллографического скольжения расширяющаяся под действием сил Пича-Келлера, создаваемых эффективным напряжением, дислокационная петля «оставила» около 1600 вогнутых дислокационных петель с обшим периметром около 350% от периметра петли и площадью 27% от площади дислокационной петли. В нижней части, рис.4 приведены распределения основных параметров островов: площадей (1), периметров (2), число стопоров вдоль границы (3). среднего расстояния между стопорами вдоль границы (4). Эти распределения сохраняют форму во всех ЭВМ-экспериментах

На рис 5 приведены некоторые вероятностно-геометрические характеристики «усредненных» островов (а,б) и островов максимальных размеров (в) в зависимости от номера К машинных экспериментов: а) 1 - средние расстояния между стопорами вдоль границ островов /*>. 2- то же, для островов максимальных размеров, 3 - площадь острова LS*), 4 - количество стопоров вдоль границы острова (N), 5 - периметр границы острова (Р*); б,в) - отношение концентраций стопоров /-го типа на границе островов и в плоскости кристаллографического скольжения. /=!,...,5, /=1 соответствует стопорам с критическим углом огибания 1,15 рад, 2 - 1,67, 3- 1,98, 4 - 2,22,5 - 2,85. Между соседними вертикальными линиями сетки рисунков длины источников одинаковы и приведены в верхней части рисунка. Отображенные параметры «усредненных» островов и островов максимальных размеров практически совпадают. Острова от дислокационных петель, сгенерированных длинными сегментами-источниками, вдоль своих границ имеют большую концентрацию сильных стопоров по сравнению с короткими источниками Поэтому следует ожидать, что они более устойчивы к процессу инволю-

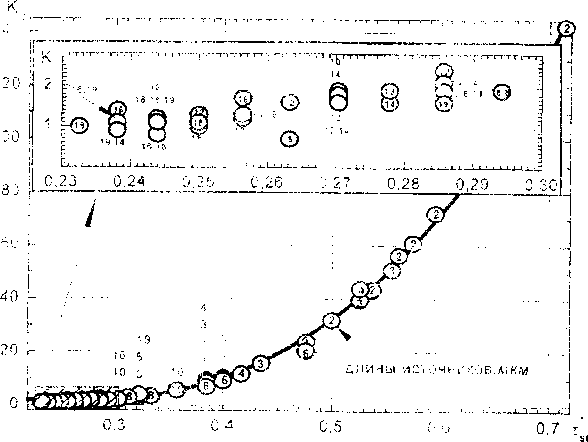
Рис 7. Число островов незавершеннот кристаллографического сдвига на 1000 пройденных препятствий (К,Л в зависимости от напряжения старта источника. Франка-Рида

Значительны изменения доли периметра вогнутых петель в периметре петли и доли их площади с распространением элементарного скольжения (см. рис.6) Кривые ria этих рисунках «выстроились» не по длинам сегментов- источников, а по напряжени- ям старта. Следовательно, характеристика количества отшнурованных вогнутых дислокационных петель должна зависеть от напряжения старта дислокационного источника. Анализ машинных экспериментов подтверждает данную гипотезу (рис.7)

На рис. 7 числа внутри экспериментальных точек - длины источников в мкл? для соответствующих экспериментов, группа чисел - кратные экспериментальные точки В таких случаях несколько экспериментов «попадают-» в близкие или одну точку.

Кластеризация - характеристика именно случайного поля препятствий. В машинных экспериментах в одном и том же поле препятствий с незначительной вариацией длины сегмента-источника острова незавершенного кристаллографического сдвига воспроизводятся. Основная их часть воспроизводи!ся и при вариации расположения сегмента-источника, если при этом существенно не меняется напряжение старта источника. Однако последовательность их образования во времени, как правило, другая

Моделирование процесса эволюции (в данном случае это инволюция, так как речь идет о сжатии вогнутых дислокационных петель) островов незавершенного кри-сталлографического сдвига при напряжении старта дислокационного источника показало [6]. что большая их часть сжимается вплоть до аннигиляции под действием сил линейного натяжения дислокации и сил Пича-Кёлера, обусловленных внешним напряжением В процессе инволюции движение элементов дислокации происходит ускоренно Кинетическая энергия такой сокращающейся замкнутой дислокации возрастает за счет 1) линейной энергии цис локации ЕД.^ связанной с островом незавершенного скольжения (У,- энергия единицы длины покоящейся дислокации, 1._п- длина линии замкнутой дислокации), 2) работы .1 сил. обусловленных внешним напряжением. В идеализированном кристалле, в котором сопротивление движению дислокаций обусловлено исключительно дискретными стопорами дислокационной природы (силы решеточною трения и вязкого торможения отсутствуют), кинетическая энергия в мо-м е н т а н н и i иля ци и

Ер =Е^>Р^ Нт„ - т_лМ^(,), (!)

где Р"- периметр замкнутой дислокации, охватывающей остров незавершенного скольжения. S’'¹'- площадь острова, напряжение прохождения источником конфи-гурашш потери устойчивости - напряжение старта источника, т,- - напряжение характеризующее дислокационную составляющую сопротивления движению прямолинейной дислокации, скользящей в таком же поле стопоров, чго и рассматриваемая замкнутая дислокация, Е_п - энергия единицы длины замкнутой дислокации, ограничивающей остров, в момент её «от иг п рибывания» от большой дислокационной петли, осуществляющей распространение элементарного скольжения Отметим, что энергия E^v' включаем в себя энергию Е„ иокоя дислокации и кинетическую энергию дислокации в момент образования острова незавершенного скольжения. Для оценок минимальной величины Ер б кристалле, идеализированном в указанном выше смысле, можно принять Ер^Е^. Первое слагаемое в (1) представляет работу' сил линейного натяжения, совершаемую при сжатии (инволюпии( острова от его исходной конфигурации (в момент возникновения) до аннигиляции Учитывая отдельным слагаемым работу сил линейного натяжения. мы можем во втором слагаемом не обращать внимания на зги силы, а описывать динамику замкнутой дислокации так. как будто эго отрезок прямолинейной дислокации, заметаюшеи такую же площадь.

Острова незавершенного кристаллографического сдвига, возникающие в процессе распространения элементарного кристаллографического скольжения, являются концентраторами диссипации энергии. Кинетическая энергия Е^, накопленная замкнутой дислокацией в процессе сокращения области незавершенного сдвига, локализуется з области её аннигиляции. При этом освобождается энергия, многократно превосходящая энергию аннигиляции покоящихся дислокаций противоположного знака, равная в расчете на межатомное расстояние вдоль дислокации приблизительно Gb³ [7]

Оценим верхнюю границу интенсивности концентрации энергии при аннигиляции замкнутых дислокаций, ограничивающих области незавершенного сдвига (дислокаций отрицательной кривизны) предположив, что аннигиляция происходит вдоль линии, длина которой того же порядка величины, что и диаметр области упругих искажений дислокации, то есть порядка р"1 2. Тогда отношение энергий (в расчете на межатомное расстояние вдоль дислокации)

я -    —           _ = р 2 А

2        1-Ес

.          Gb Gb1

Принимая         — и         имеем

Для острова на рис. 1(5) g «223.

Таким образом, острова незавершенного скольжения, образовавшиеся в результате распространения элементарного кристаллографического сдвига, являются концентратами энергии, рассеиваемой в процессе деформации. Диссипация энергии в плоскостях скольжений весьма неравномерна. В локальных областях аннигиляции замкнутых дислокаций, связанных с незавершенным скольжением, плотность энергии, выделяющейся при аннигиляции островов, может на несколько порядков величины превышать энергию, выделяющуюся при аннигиляции прямолинейных дислокаций. Поэтому энергетически возможен переход атомов в возбужденные состояния и связанные с этим электромагнитные излучения.