ГЕНЕРАЦИЯ ТРЕХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ СЛУЧАЙНЫХ ЧИСЕЛ ДЛЯ КРИПТОГРАФИЧЕСКИХ СИСТЕМ ЗАЩИТЫ ИНФОРМАЦИИ

Генерация случайных сигналов представляет собой достаточно востребованное направление в различных областях научных исследований и техники [1; 2; 3]. В области криптографической защиты информации значительное внимание уделяется генераторам псевдослучайных чисел (ГПСЧ), в основе которых лежит алгоритм, реализующий математическую модель генерации [4–7]. Известные подходы имеют ряд недостатков, касающихся статистических характеристик генерируемой последовательности и ее длительности. То есть, использование ГПСЧ в качестве гамма-последовательности является достаточно уязвимым решением, так как по небольшому отрезку известных значений может быть восстановлен весь ряд случайных чисел [8]. Таким образом, актуальной является задача разработки такого генератора случайных чисел, восстановление полного ряда которого по известному ряду значений невозможно или крайне затруднительно.

Задача генерации случайных чисел

В общем случае ГПСЧ представляет собой функцию, входом которой является набор параметров, определяющих генерируемый ряд. Рассмотрим алгоритм Блюм-Блюма-Шуба [9], где для генерации чисел используется функция с обратной связью. Входным значением является результат решения функции на предыдущей итерации. В данном алгоритме повторение генерируемого ряда произойдет тогда, когда в результате работы генератора повторится начальное значение ряда. При этом восстановление предыдущего значения итерации осложняется использованием функции остатка от деления нацело, что требует решение задачи факторизации. Таким образом, данный алгоритм обладает хорошими криптографическими свойствами и большим периодом повторения. Одно из возможных решений по увеличению периода повторения описано в работе [10], где предлагается формирование двух последовательностей случайных чисел, где каждый из генераторов использует на входе результаты работы обеих генераторов на предыдущей итерации. К достоинствам предложенного решения следует отнести меньшую вероятность повторения ряда, так как теперь, для повторения ряда чисел требуется совпадение начальных значений двух генераторов и возможность генерации двух последовательностей случайных чисел. Однако данное решение не обеспечивает устойчивость к потенциальному решению задачи факторизации и не исключает взаимную стохастическую связь значений между соседними значениями, так как результат работы функции на одной итерации является аргументом функции на следующей итерации.

Генерация трех последовательностей случайных чисел

В целях совершенствования существующих решений предлагается реализация генератора трех независимых последовательностей незави-

[й

BY

симых случайных чисел. Такое решение позволит снизить взаимную стохастическую связь между генерируемыми значениями и усложнить вычисление значений предыдущей итерации.

Рассмотрим математическую модель генератора трех последовательностей случайных чисел. Для этого построим выражения, описывающие генерацию каждого из рядов случайных чисел, являющихся функциями двух, сгенерированных на прошлой итерации значений:

x i + 1 = f ( y i , z i ) ' y + 1 = f ⁽ x , z i)>■ z i + 1 = f (x i , y i ) ,

Заметим, что функция генерации каждого из значений имеет аргументом результат генерации двух других функций, что значительно снижает стохастическую связь между соседними генерируемыми значениями в каждом ряду генерируемых значений. Построим функции генерации:

xi + i = { a i yi ⁺ b zi ⁺ c i yi /zi ^} y , + 1 = ^{ a 2 ^zi ⁺ b 2 xi ⁺ c 2 z i /xi ^} ■ zi + i = ^{{ a} 3 xi ⁺ b 3 yi ⁺ c 3 xi!yi ^}

Коэффициенты a, b, c уравнений (2) подбираются с целью получения оптимальных статистических характеристик генерируемых последовательностей. Начальные значения x 1, y 1, z 1 являются ключом. Изменение начальных значений приводит к генерации новых последовательностей.

Сформируем на основе выражений (1) структурную схему ГПСЧ (рисунок 1). Структурная схема содержит три идентичных функциональ- ных блока 1, 2 и 3 для генерации значений x, y и z соответственно, с тремя входами и двумя выходами. На первые входы поступают начальные значения (значения ключей). Вторые и третьи входы соединены с первыми выходами двух других блоков.

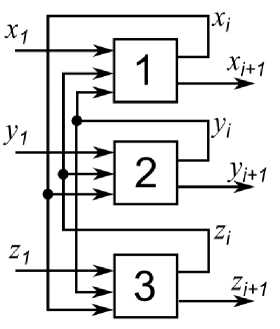
Рисунок 1. Структурная схема ГПСЧ

При этом структура каждого из трех блоков (рисунок 1) имеет одинаковый вид, приведенный на рисунке 2. Заметим, что обозначения входов и выходов на рисунке 2 даны для первого функционального блока, однако, изменение блока приведет лишь к изменению входных значений в соответствии с рисунком 1.

Каждый функциональный блок (рисунок 1) содержит блок 1 памяти коэффициентов (БП) a, b, c (рисунок 2), блоки 2, 3, 4 умножения, к первым входам которых подключены выходы блока 4, а ко вторым входам подключены входы функционального блока, блок 5 деления, к первому входу которого подключен второй вход функционального

Функциональный блок

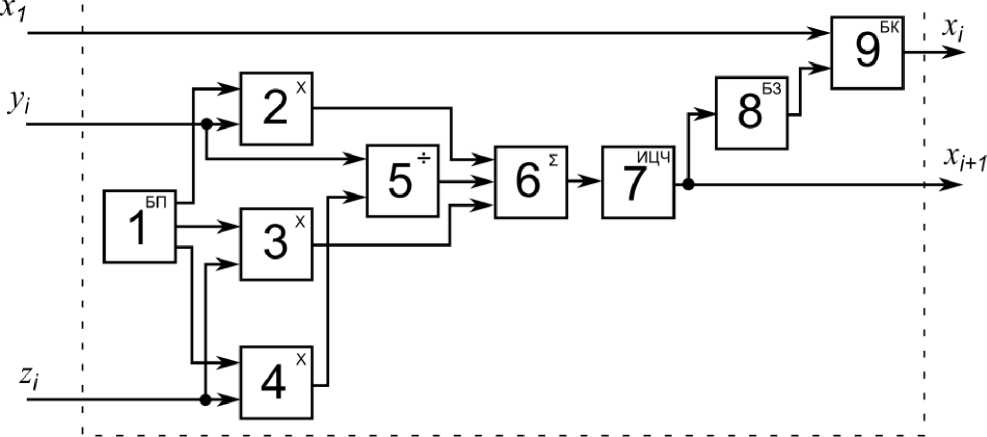
Рисунок 2. Структурная схема блоков ГПСЧ

блока, а ко второму входу подключен выход блока 4, блок 6 суммирования, ко входам которого подключены выходы блоков 2, 3, 5, а выход которого подключен к входу блока 7 с исключением целой части (ИЦЧ), выход блока 7 подключен ко входу блока 8 задержки (БЗ) и является вторым выходом функционального блока, блок 9 коммутации, первый вход которого подключен к первому входу функционального блока, второй вход подключен к выходу блока 8, а выход является первым выходом функционального блока. Устройство работает следующим образом. Каждый из трех функциональных блоков работает идентично. На первом шаге блоки 9 коммутации передают на первые выходы функциональных блоков начальные значения (значения ключей) с первых входов, которые по обратной связи передаются на соответствующие входы функциональных блоков. Начиная со второго шага работы устройства, блоки 9 коммутации передают на первые выходы функциональных блоков значения с блоков 8 задержки на один отсчет. Работа функционального блока основана на выражениях (2). Умножители 2, 3 и 4 формируют три слагаемых, причем значения коэффициентов a , b и c берутся, соответственно, с первого, второго и третьего выходов блока 1 памяти. Блок 5 реализует деление в третьем слагаемом, блок 6 осуществляет сложение трех слагаемых. Блок 7 исключает целую составляющую из полученного в блоке 6 значения, после чего результат передается на второй выход функционального блока и на блок 8 задержки, для последующего использования результата на следующем шаге.

Выходной сигнал, каждого из трех функциональных блоков представляет собой последовательность случайных чисел, определяемую коэффициентами a , b и c и начальными значениями (ключами).

Компьютерное моделирование

Моделирование генератора выполнено на языке программирования Python. Определим массивы рядов псевдослучайных чисел, задавшись произвольными начальными значениями. Листинг кода:

a1=0.65; a2=0.5; a3=0.55

b1=0.6; b2=0.55; b3=0.7

c1=4; c2=3.6; c3=4.3

n=100000

x[0]=0.6;y[0]=0.55; z[0]=0.65

Величина n определяет количество чисел в массиве каждого ряда.

Формирование цикла вычисления случайных чисел в соответствии с выражениями реализуется следующим кодом:

for i in range(n-1):

x[i+1]=(a1*y[i]+b1*z[i]+c1*y[i]/z[i])%1 y[i+1]=(a2*x[i]+b2*z[i]+c2*z[i]/x[i])%1 z[i+1]=(a3*x[i]+b3*y[i]+c3*x[i]/y[i])%1

В результате получим три массива случайных чисел. Визуализация полученных чисел представлена на рисунке 3 в виде точечных графиков. Жирными точками показаны значения массива x , маленькими точками значения двух других массивов. Результат приведен для первых 1000 отсчетов каждого массива.

Проведем анализ полученных значений. Проанализируем распределение значений. Для этого построим гистограмму значений, поделив все значения на две «корзины». Результат для трех каналов приведен на рисунке 4. Приведены распределения значений по двум корзинам для трех массивов значений.

О        250       500       750       1000       1250      1500      1750      2000

Рисунок 3. Визуализация полученных значений случайных чисел

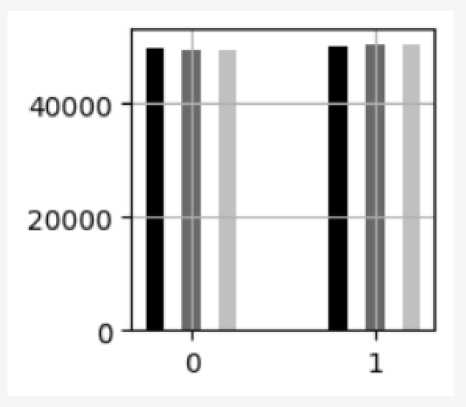
Рисунок 4. Распределение значений по двум «корзинам»

На рисунке 5 приведено распределение значений по десяти «корзинам», то есть 0..0,1, 0,1..0,2 и т.д. Видно, что значения равномерно распределяются во всем диапазоне возможных значений. Эксперименты с большим количеством корзин привели к аналогичному результату – к равномерному распределению значений.

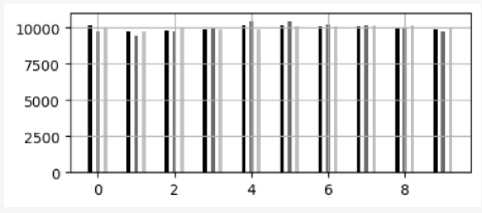
Рисунок 5. Распределение значений по десяти «корзинам»

Таким образом, генератор дает значения, равномерно распределенные во всем диапазоне от нуля до единицы.

Рассчитаем статистические характеристики полученных массивов.

Математическое ожидание по выходам:

x : 0,5009276269407209

y : 0,503412071585185

z : 0,5026476352807453

Дисперсия по каналам по выходам:

x : 0,08294137402589338

y : 0,08162625720105295

z : 0,08320368092229136

Стандартное отклонение:

• x : 0,28799544098109153

y : 0,2857030927397408

z : 0,2884504826175393

Проанализируем статистическую связь между массивами случайных значений. Для этого найдем ковариацию и коэффициент корреляции массивов попарно.

Ковариация:

x , y : -0,00012238879458405428

y , z : -0,00013971923270529853

z , x : - 0,00022766764314654492

Коэффициенты корреляции:

x , y : -0,001487430765140954

y , z : -0,0016953744638278099

z , x : - 0,002740564866956251

Проведем анализ в пределах каждого массива Сравним массив с самим собой, смещенным на один отсчет для установки стохастической связи между соседними отсчетами. В каждом генераторе на вход поступают зачения с двух других генераторов, что должно обеспечить отсутствие стохастической связи между соседними значениями. Для этого получим значения ковариации, сравнивая каждый массив с самим собой, смещенным на 1 отсчет. Ковариация в каналах при смещении:

x: -0,00044465370813492156

y: -0,00013004483682494856

z: -0,00023188457220133324

Видно, что связь между соседними значениями отсутствует.

Выводы

Исследование разработанного генератора трех последовательностей случайных чисел показало, что предлагаемое решение обладает рядом достоинств, а именно:

Генерируются три независимые последовательности независимых случайных чисел, определяемые коэффициентами алгоритма и начальными значениями, что может быть полезно для решения задач криптографического шифроания и пространственного моделирования.

Три массива генерируемых значений имеют равномерное распределение в диапазоне больше нуля и меньше единицы.

Возможно объединение массивов необходимым образом.