Генерация внеосевых оптических ловушек на основе пучков со степенной фазовой зависимостью от радиуса

МОДЕЛИРОВАНИЕ

Развитие методов оптической микроманипуляции [1 - 3], используемых в широком спектре задач, которые связаны с захватом и переносом частиц, молекул и атомов [4 - 6], является перспективным направлением развития лазерной физики и прикладной оптики. Основным подходом для захвата частиц является создание оптических ловушек [7 - 9]. При использовании обычных световых ловушек, когда частица притягивается в область максимальной интенсивности, нагрев частицы может привести к ее разрушению.

Альтернативой является захват частицы в зоне с минимальной интенсивностью, в «световой бутылке» [10 - 12]. Такие ловушки представляют собой область нулевой интенсивности, окруженную областью более высокой интенсивности, которая представляет собой световой барьер.

Одним из способов формирования областей с минимальной интенсивностью является использование лазерных пучков с винтовой фазовой сингулярностью [13 - 15], причем градиент фазы позволяет вращать захваченные частицы. Однако такие ловушки фактически являются двумерными, т.к. теневая область ограничивается только поперечным световым барьером. При использовании «световых бутылок» обеспечивается трехмерный захват поглощающих и менее плотных чем окружающая среда частиц [16, 17].

Распределение амплитуды пучков в параксиальной области описывается преобразованием Френеля:

ik .

F(u, v,z) =-- exp(ikz") •

2^z

• U f(x, y) exp g ((x — u)² + (y — v)²)) dxdy,

^(x — u) ² + (y — v) ² « z. (1)

Если комплексная функция пропускания входного пучка может быть представлена в виде f(r, ф) = А(г)е1тф, где m - целое число, то выражение (1), представленное в полярных коор- динатах, упрощается до однократного интеграла и может быть представлено в виде:

F_m(p,9,z) = -—exp(ikz) exp(im9) exp (——) • z                         2z )

^ю           ikr² krp

• J„ Л(Г)еХР("27);т(— )rdr’   (2)

где J_m(x) – функция Бесселя порядка m .

В случае, когда входная функция обладает осевой симметрией (m = 0), формируемое поле не зависит от угла, а для вычисления распределения на оптической оси полагается p = 0.

Классическая параболическая линза с ком- плексной функцией пропускания ikr2^

f(r) = exp I-2f ^,

где к = 2л/Л - волновое число для лазерного излучения с длиной волны А = 0,000532 мм, f = 1000 мм – фокусное расстояние, позволяет получить максимум интенсивности на оптической оси в плоскости фокуса z = f .

Добавление аксиконов [18, 19] позволяет изменять положение фокуса вдоль оптической оси. Таким образом, использование рассеивающего аксикона exp(ikar) обеспечивает максимум интенсивности на оси после фокуса линзы, а собирающего exp(-ikar) - обеспечивает максимум интенсивности на оси до фокуса линзы. Здесь а принимает значения больше 0.

При равных значениях а смещение, порождаемое рассеивающим аксиконом больше, чем смещение, порождаемое собирающим ак-сиконом, поскольку добавляется влияние собирающей компоненты линзы, и разность этих смещений увеличивается по мере увеличения параметра а [20]. При этом при использовании рассеивающего аксикона энергия в точке максимума падает по мере удаления от начальной точки фокуса, поскольку увеличивается длина по полуспаду, и энергия распределяется на большую площадь.

На рисунке 1 показано распределение интенсивности на оси классической линзы (сплошная линия), а также линзы с использованием рассеивающих аксиконов с различными параметрами а.

Использование совокупности аксиконов (или бинарного аксикона [21, 22]) позволяет формировать сразу два локальных максимума на оптической оси, до и после фокуса линзы [23]. Между максимумами находится кольцевое распределение интенсивности, при этом энергия на оптической оси нулевая. Таким образом, частицы, заключенные в области низкой интенсивности, окруженной световым барьером (т.е. в оптической бутылке), могут быть удержаны и перемещены.

Возможно как использование совокупности аксиконов, описываемое выражением cos(kar), зависящие от одного параметра, так и совокупности, где «1 и а2 различны (например, «1 = -0,000266 и «2 = 0,000798). В первом случае локальный максимум, образованный фокусирующим аксиконом всегда больше локального максимума, образованного рассеивающим ак- сиконом из-за влияния линзы.

/ ( г ) = c _o exp

/ 1кг2

U/J

cos(kar).

Разница между распространением интенсивности на оси при использовании линзы и при использовании комбинации из линзы и ак-сиконов представлена на рисунке 2.

С увеличением параметра α расстояние между максимумами интенсивности увеличивается. Первый фокус смещается к входной плоскости, второй отдаляется от нее. Более короткий фокус соответствует более сильной фокусировке. Важно отметить, что не для всех значений а энергия в точке фокуса нулевая.

Варьирование параметра а позволяет варьировать размер оптической ловушки. Тем не менее, чем длиннее ловушка, тем меньше энергии приходится на ее стенки, поэтому существует предел, связанный с энергией захваченной частицы.

Оптические ловушки, формируемые с помощью пучков, описываемых выражением (4), расположены на оптической оси. Для возможности захвата частицы вне оси можно использовать оптический клин или фазовую добавку с отклоняющим волновым фронтом [24, 25], в этом случае входная функция пропускания описывается выражением:

1кг²\   „ ' v

/ ( г ) = exp ^yj cos(kttr) д C y exp^k^.y) . (5)

Поскольку функция (5) является симметричной только относительно оси x , для моделирования распространения оптического пучка используется преобразование (1).

Параметр ^ влияет на отклонение от оптической оси. Если ^ > 0, фокус смещается в положительном направлении оси y , иначе – в отрицательном.

На рисунке 3 показана возможность создания сразу двух оптических ловушек, одна из которых может захватывать частицу над оптической осью, другая – под ней. В этом случае смещение относительно оптической оси одинаковое, поскольку равные по модулю ^ и ^ образуют симметрично расположенные ловушки.

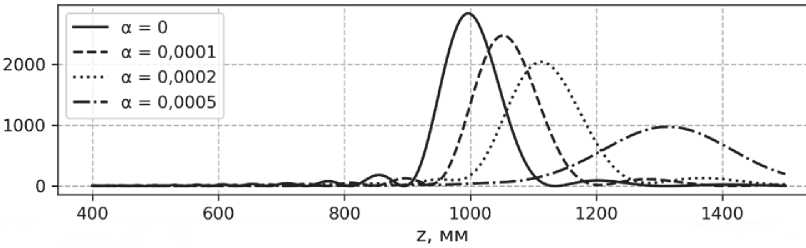
Рис. 1. Влияние параметра рассеивающего аксикона на распространение интенсивности на оптической оси

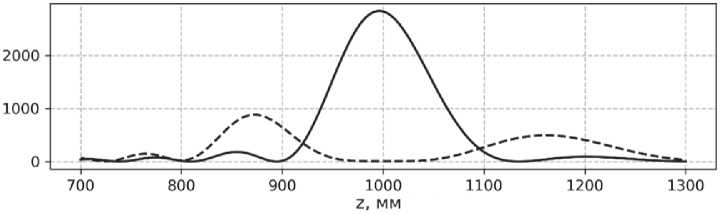
Рис. 2. Распределение интенсивности на оптической оси при использовании линзы (сплошная линия) и при использовании линзы и совокупности аксиконов (пунктирная линия), а = л/к

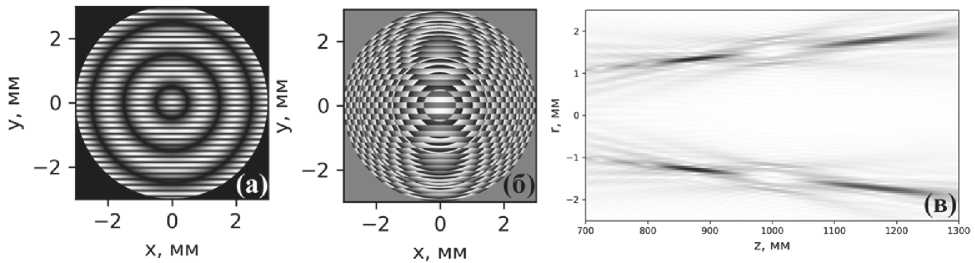
Рис. 3. Амплитуда (а) и фаза (б) оптического элемента, а также амплитуда (негатив) сформированного распределения оптических ловушек (в), |^ _т | = |^ ₂ | = 0,0015

Тем не менее поскольку положение и размер ловушек зависят от положения фокуса линзы, коэффициента аксиконов и смещения, то мы можем генерировать ловушки, не связанные друг с другом общими характеристиками, как это показано на рисунке 4. Для этого комплексная функция пропускания (4) заменяется на сле- дующую:

^f^^

cos(ka₇r)exp(tk^_/.y) .(6)

Как можно видеть из рисунка 4, первая ловушка расположена ближе к оптической оси и наклонена к ней под меньшим углом. Центры каждой ловушки расположены в точках фокуса соответствующих линз. Сохраняется нулевая интенсивность внутри ловушек и кольцевое распределение вокруг.

ЗАКЛЮЧЕНИЕ

В работе рассмотрены свойства распространения пучков со степенной фазовой зависимостью от радиуса. Показано, что при дополнении фокусирующих линз рассеивающими и собирающими аксиконами возможно создавать оптические ловушки, которые могут найти применение во многих отраслях науки.

Возможно как создание оптических ловушек на оптической оси, так и внеосевых ловушек с помощью фазовых добавок с отклоняющим волновым фронтом. Для контроля положения ловушек в пространстве используются как разные фокусные расстояния линз, соответствующие конкретным ловушкам, так и различные параметры смещения, позволяющие генерировать ловушки под разными углами к оптической оси.

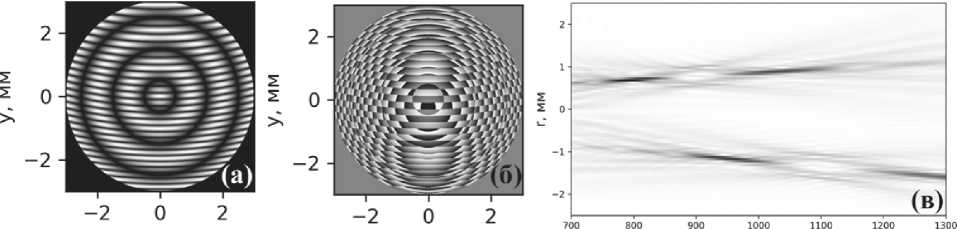
X, ММ                      х, ММ                              z’ мм

Рис. 4. Амплитуда (а) и фаза (б) оптического элемента, а также амплитуда (негатив) сформированного распределения оптических ловушек (в) при /₁ = 900, /₂ = 1100, ^ = 0,001, ^₂ = -0,0015, а₁ = а₂ = л/к

Размер ловушки может варьироваться посредством изменения параметра аксиконов, тем не менее, стоит в первую очередь отталкиваться от энергии частиц, поскольку при увеличении размера ловушки энергия в ее стенках уменьшается.