Генерация второй гармоники в порошках кристаллов ниобата бария стронция

Генерация второй гармоники (ГВГ) широко используется для получения лазерного излучения в новых спектральных диапазонах. Поиск новых нелинейных кристаллов, исследование их нелинейно-оптических характеристик является актуальной задачей современной лазерной физики. Среди твердотельных нелинейно-оптических материалов особое место занимают сегнетоэлектрические твердые растворы ниобата бария-стронция SrxBa1-xNb2O6 (SBN-x), которые относятся к классу «активных диэлектриков» – диэлектриков, проявляющих качественно новые свойства под влиянием внешних воздействий.

Кристаллы ниобата бария-стронция обладают высокими значениями диэлектрической проницаемости, высокими пиро-, пьезо- и электрооптическими коэффициентами. SBN характеризуется высокими нелинейно-оптическими параметрами, поэтому может рассматриваться в качестве перспективного материала для создания эффективных удвоителей частоты [1; 5–6; 10]. Легирование кристаллов SBN ионами редкоземельных и переходных металлов приводит к появлению примесных дефектов в кристаллах, изменению их фазового состояния, приводящего к изменению оптических и нелинейных характеристик [1; 5].

ВЕСТНИК Мордовского университета | 2014 | № 1-2

Из-за малого двулучепреломления SBN условия фазового синхронизма для удвоения частоты лазерного излучения в видимой и ближней ИК области спектра не реализуются. Однако на основе сегнетоэлектрических кристаллов SBN можно создать элементы с периодической модуляцией доменной структуры, которые могут быть интересны для разработки компактных эффективных ГВГ. Целью данной работы было получение ГВГ в номинально чистых и легированных кристаллах SBN, а также исследование зависимостей эффективности ГВГ от состава и температуры нелинейной среды.

Известно, что в оптической среде вектор поляризуемости связан с вектором электрической напряженности электромагнитного поля нелинейным материальным уравнением:

P = z a k ( Е ) E_k ,         (1)

k где αik(E) можно разложить в ряд по степеням напряженности электромагнитного поля Е как:

a(E)=a+E XikjEj +

. j = 1

3 3

,             (2)

ikjm jm ...

j = 1 m = 1

где α _ik – линейная восприимчивость; χ _ikj – квадратичная нелинейная восприимчивость; θ _ikjm – кубическая нелинейная восприимчивость.

За процесс ГВГ отвечает коэффициент χikj, который отличен от нуля в среде с нецентросимметричной структурой и обращается в ноль в центросимметричной среде. В изотропной нелинейной среде при коллинеарном взаимодействии волн интенсивность излучения на удвоенной частоте I(2ω) будет квадратично расти до тех пор, пока излучение идет синфазно с основным излучением I(ω). Из-за дисперсии на длине порядка длины когерентности lког = π /∆k, где ∆k=(k(ω)-k(2ω)), возникает волновая расстройка, которая приводит к уменьшению I(2ω) [4]. Поэтому для эффективной ГВГ обычно выбирают кристаллы с двулучепреломлением, в которых существуют направления распространения, вдоль которых выполняются условия фазового синхронизма. В отрицательных одноосных кристаллах основная волна I(ω) будет обыкновенной, а волна второй гармоники I(2ω) – необыкновенной и тогда условие фазового синхронизма можно записать в виде no (to) = ne (2rn).

Схема экспериментальной установки для исследования ГВГ в порошках SBN представлена на рис. 1. Одномодовый одночастотный YAG:Nd-лазер, работающий на длине волны 1,064 мкм с частотой следования импульсов 5 Гц, давал лазерные импульсы с энергией около 10 мДж и длительностью 12 нс. Фазовая пластинка λ /2 и призма Глана позволяли плавно изменять энергию импульсов лазерного излучения при сохранении его остальных характеристик: направления, расходимости, длительности импульса, когерентности.

Часть излучения лазера отводилась плоскопараллельной пластинкой на измеритель энергии лазерного излучения Ophir Nova-II (ФП), что давало амплитуду опорного луча, пропорциональную энергии возбуждающего излучения. После коллимации излучение на основной частоте ω направлялось на образец. Порошок исследуемого образца помещался на стеклянную подложку, находящуюся на медном блоке, температура которого менялась в диапазоне от 5 до 90 ^oC и контролировалась термопарой. Температура изменялась путем прокачки воды помпой терморегулятором, которая поддерживала температуру постоянной с точностью ±3^о.

При облучении возбуждающим излучением в порошке исследуемого вещества визуально наблюдалась генерация второй гармоники, излуче- ние зеленого света. Это излучение собиралось короткофокусной линзой и коллиматором в волоконный световод и направлялось на вход спектрометра USB4000-UV-VIS, Ocean Optics. Спектр рассеянного излучения анализировался

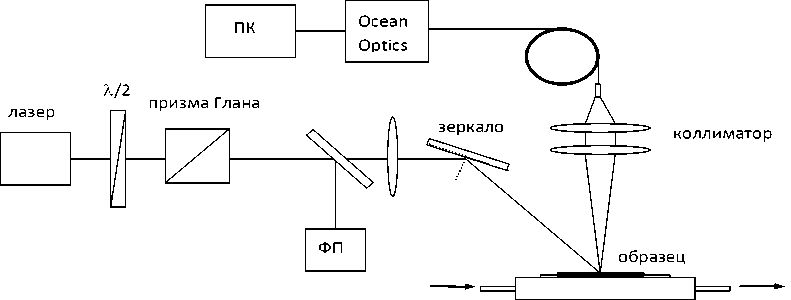
Р и с . 1. Экспериментальная установка для исследования ГВГ в порошках кристаллов SBN

Из-за низкого двулучепреломления в кристаллах SBN отсутствуют направления, удовлетворяющие условию фазового синхронизма для ГВГ излучения с длиной волны 1,064 мкм. Поэтому в объемных образцах SBN ГВГ неэффективна. В работе были исследованы порошки кристалла SBN с размером зерен порядка длины когерентности. В табл. 1 представлены литературные данные по величине показателя преломления для обыкновенного и необыкновенного луча на длине волны при помощи программы SpectraSuite. В спектре наблюдался интенсивный пик ГВГ на длине волны 532 нм, амплитуда которого была пропорциональна энергии импульса излучения на удвоенной частоте.

Серия «Естественные и технические науки»

1 064 нм и 532 нм, а также расчетные значения длины когерентности для ГВГ в направлении, перпендикулярном оптической оси кристалла. Для этого использовалось выражение [9]:

l kog =

λ

4( n e (2 _Ю ) - n o ( _Ю ))^.

Видно, что в кристаллах SBN длина когерентности для ГВГ излучения с длиной волны 1 064 нм равна 3–5 мкм.

Т а б л и ц а 1

Рассчитанные длины когерентности для ГВГ излучения с длиной волны 1 064 нм в кристаллах SBN и данные по показателям преломления [8]

Кристалл	nо(ω)	nе(2ω)	nе(2ω)- nо(ω)	lког , мкм
SBN-61	2.25	2.326	0,076	3,487
SBN-75	2.25	2,341	0,091	2,912

Экспериментальные образцы исследуемых порошков изготавливались из номинально чистых кристаллов SBN-61, SBN-75 и SBN-61, выращенных из расплавов, легированных 0,5 вес.% Nd O , 0,5 вес.% Ni2O3, 0,01 вес.% Cr2O3 и 02,031

вес.% Cо3O4. В качестве образца сравнения использовался порошок из кристалла LiIO3. Образцы кристаллов объемом около 10 мм3 перетирались в яшмовой ступке. Измерение размера частиц порошка проводилось с помощью оптического ми- кроскопа, сопряженного с фотокамерой и персональным компьютером и показали, что основную часть порошка составляют частицы SBN размером <5 мкм, то есть порядка длины когерентности для ГВГ излучения с длиной волны 1 064 нм.

Нами была измерена интенсивность излучения второй гармоники при ГВГ в порошках кристаллов SBN и LiIO3 в зависимости от энергии падающего на образец излучения. Полученны экспериментальные зависимости представлены на рис. 2. Видно, что полу- ченные экспериментальные кривые хорошо описываются квадратичной зависимостью (рис. 2 б). Крутизна энергетической зависимости определяется величиной квадратичной нелинейной восприимчивости (рис. 2 а). Согласно рис. 2, в номинально чистом кристалле SBN-61 (2), кристалле SBN-61, легированном Cо (1) нелинейность несколько выше, чем в кристалле SBN-61:Cr (3) и LiIO3 (4). В кристаллах SBN-61:Ni (5), и SBN-75 (6) нелинейность значительно ниже, чем в других кристаллах.

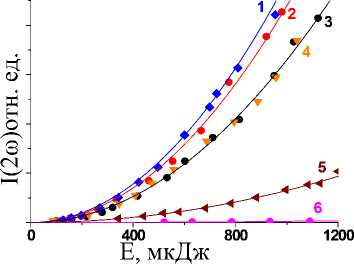
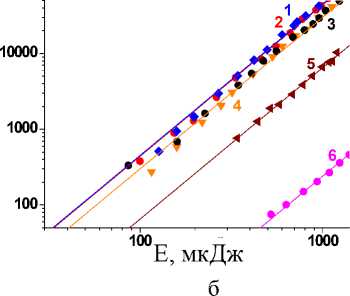
Р и с . 2. Зависимости интенсивности второй гармоники при ГВГ излучения с длиной волны 1,064 мкм от энергии падающего на образец излучения в линейном (а) и двойном логарифмическом (б) масштабе, 1 – SBN-61:Cо; 2 – SBN-61; 3 – SBN-61:Cr; 4 – LiIO3; 5 – SBN 61:Ni; 6 – SBN-75

ВЕСТНИК Мордовского университета | 2014 | № 1-2

Полученные экспериментальные данные были аппроксимированы квадратичными зависимостями вида Y = A·X2 (сплошные линии на рис. 2). Коэффициент А пропорционален квадрату квадратичной нелинейной восприимчивости χ в среде. Значения χ для кристаллов SBN были рассчитаны относительно известного значения χ для кристалла LiIO3 (табл. 2). Видно, что величина χ варьируется в широком диапазоне от 16,3·10-12 до 1,2·10-12 м/В в зависимости от собственного и примесного состава кристалла SBN.

Т а б л и ц а 2

Коэффициенты (А) и расчетные относительные значения квадратичной нелинейной восприимчивости в исследованных кристаллах при Т=300 К

Кристалл	А, отн. ед.	χ, 10-12 м/В
SBN-61:Co	0,04500	16,3
SBN-61	0,04400	16,1
SBN-61:Cr	0,03300	14,0
LiIO3	0,03300	14,0
SBN-61:Ni	0,00650	6,2
SBN-75	0,00024	1,2

На рис. 3 представлены температурные зависимости интенсивности ГВГ в порошках исследованных кристаллов. Энергия излучения основной гармоники, длительность импульсов генерации и условия фокусировки в течение эксперимента оставались постоянными. Из рисунка видно, что в кристалле LiIO3 интенсивность ГВГ в данном температурном интервале остается практически постоянной. В кристаллах SBN с ростом температуры наблюдается уменьшение эффективности ГВГ, причем зависимости имеют характерный излом. Кристаллы SBN характеризуются размытым фазовым переходом из сегнетоэлектрической полярной фазы в параэлектрическую неполярную фазу. Температура фазового перехода зависит от собственного и примесного состава кристалла SBN. На рис. 3 показано, что в кристаллах SBN-61 и SBN-61:Cr излом наблюдается при температурах 77 и

72 оС. В образцах SBN-61:Nd, SBN-61:Ni и SBN-75 он наблюдается при более низких температурах: 50, 45 и 35 оС соответственно.

Наблюдаемый изгиб в температурной зависимости, видимо, определяется температурой фазового перехода. Дальнейшее повышение температуры образцов приводит к плавному снижению интенсивности второй гармоники вплоть до ее полного исчезновения. Отметим, что при последующем охлаждении всех исследуемых образцов происходило восстановление нелинейных свойств, что свидетельствовало об отсутствии эффекта гистерезиса в данном температурном диапазоне. В табл. 3 показано, что полученные экспериментальные значения температуры фазового перехода согласуются с литературными данными, полученными другими экспериментальными методами [2; 7].

Серия «Естественные и технические науки»

SBN-61

LiIO3

SBN-61: Nd

SBN-61: Cr

SBN-61: Ni и н о

S

SBN-75

40        60

T, оС

Рис . 3. Зависимость интенсивности второй гармоники при ГВГ от температуры образца

Заметим, что вторая группа образцов также характеризуется более низкой эффективностью ГВГ при комнатной температуре, причем в SBN-75 она была приблизительно в 200 раз ниже, чем в SBN-61.

Это свидетельствует о том, что образцы SBN разного состава при комнатной температуре находятся в различных фазовых состояниях, для которых характерно уменьшение величины квадратичной не- линейной восприимчивости. Полученные данные могут дать информацию о степени нецентросимметричности фазового состояния кристаллов SBN в зависимости от их собственного и примесного состава и температуры.

Т а б л и ц а 3

Зависимость температуры фазовых переходов в SBN от состава

Кристалл	T ФП , °C
	Настоящая работа	Литературные данные
SBN-61	77	81 [2]
SBN-61:Cr	72	77 [7]
SBN-61:Ni	50	54 [Там же]
SBN-61:Nd	45	61 [2]
SBN-75	32	40–50 [Там же]

Итак, впервые при помощи ГВГ был исследован фазовый переход в твердых растворах SBN из сегнетоэлектрической полярной фазы в параэлектриче-скую неполярную. Нами было показано, что фазовый переход характеризуется плавной зависимостью от температуры с характерным изломом, определяемым температурой фазового перехода в среде. В ходе работы было установлено, что в ряде кристаллов SBN, для которых характерна низкая температура фазового перехода, при комнатной температуре наблюдается низкая эффективность ГВГ.

Проведенные исследования показали, что твердые растворы SBN-61, SBN-61:Cr обладают высокой квадратичной нелинейностью при комнатной температуре и могут быть перспективными для создания удвоителей частоты, нелинейных элементов с регулярной периодически модулированной доменной структурой для реализации условий квазисинхронизма. Зависимость величины квадратичной нелинейной восприимчивости в SBN от температуры может быть использована для изготовления нелинейных оптических элементов для ГВГ с эффективностью преобразования, контролируемой температурой среды.

ВЕСТНИК Мордовского университета | 2014 | № 1-2