General Research on Automatic Image Shrinking in the Wireless Capsule Endoscopy

Published Online April 2012 in MECS DOI: 10.5815/ijigsp.2012.03.04

Wireless capsule endoscopy is a modern non-invasive method of the gastrointestinal tract examination.

Capsule endoscopy has provided clinicians with the non-invasive ability to detect abnormal changes of the gastrointestinal tract (generally in small bowel) often missed by other techniques. [1], [2].

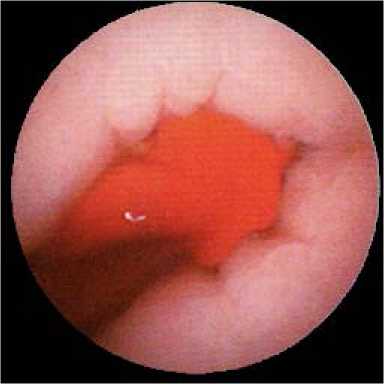
Figure. 1. Image of the gastrointestinal tract in the wireless capsule endoscopy.

The possibility of capsule to make an automatic analysis is now of great interest because of its potential in recognition of pathologies in any part of gastroenterological tract. However, this method of examination of the gastrointestinal tract requires a lot of memory for data storage [3].

This article is devoted to image shrinking method without loss of the quality with regard to a modern field in medical research - wireless capsule endoscopy.

Person swallows a tiny capsule that takes pictures of his digestive tract. In the diagnosis of the gastrointestinal tract wireless capsule travels taking two images per second and by the end of the examination there are more than 57,000 images (as shown in Fig. 1). After that images are transmitted to a desktop computer for further processing. In the end this images are analyzed be a physician [4].

One of the most important issues of the wireless endoscopy system is providing sufficient capacity of the transmitter, the power supply duration and the equipment size. The decrease of the transmitted information will increase image acquisition frequency reducing energy consumption. As a result endoscopic capsule may work significantly longer. Thus, there is a problem of image shrinking inside the capsule in order to get more data for analysis without increasing the size of the device.

• III.    shrinking schemes

Data from the camera of the wireless capsule are transmitted to the memory on the principle of FIFO (First In - First Out) [5]. From the memory the array comes on the shrinking chip over a single-bit port. The color image pixel is determined by three components of the scheme RGB (Red, Green, Blue). Then the data are shrunk and sent over an 8-bit port to the transmitter. Capsule transmitter sends code words to the external receiver which decodes the image.

The scope of the device imposes strict restrictions on the shrinking scheme [6]:

• •    Low power consumption - capsule works on battery and high energy consumption will reduce the time of work.

• •    Memory array is updated twice a second - the time of shrinking should not exceed this limit.

• •    The size of capsule is 1.5-2 cm. It imposes a limit on the chip size. The best option will be a chip 5х5mm.

According to the requirement of the device for data shrinking without the loss the following algorithms were chosen:

• •    Triplets coding of binary combinations (TC);

• •    Conversion combination MTF (move-to-front) [7], and Rice coding.

• A.    Triplets coding of binary combinations

Triplets coding of binary combinations refers to the universal coding. In the universal coding statistical redundancy in the sequence obtained after coding tends to zero with the length increasing of the blocks into which the original binary sequence is divided.

This method is designed to shrink the binary data in an unknown statistics of the message source. The method is used when it is needed to restore exactly the original binary sequence and data shrinking is unacceptable due to information loss [8], [12], [13], [14].

The original sequence of binary data is divided into blocks of n bits. For each block three parameters are determined:

• •    The number of units in the block - k ;

• •    The sum number of their positions - s ;

• •    The number of this particular combination in the corresponding class (element of the intersection of the multitudes K and S ) - b (n, k, s).

It is proved that the redundancy R n in the dataflow output tends to zero with the length increasing of the original blocks n . It means that coding is asymptotically optimal:

limR n =0, where                               (1)

n →∞

R_{n –} coding redundancy:

Rn=sup Rn (р), where о<р<1

Rn (р) = nср/n -Н (р), where nср is average length of code word,

Н (р) = -(p log 2 p+q log 2 q) – entropy of the source.

The number of each code combination is calculated by the formula:

b(n,k,s)= R (i k –1, K , i k + i k-1 +...+ i 1 )+ R (i k-1 –1, K -1, i k- ₁+ i_k-2...+i₁)+ …+ R (i₂ – 1, 2, i₂+ i₁ ) =

= ∑ ^k    R ( i j – 1, J , ∑ ^j    i m ),                         (2)

j = 2                    m = 1

where i is the number of the unit position in the original block [8].

For the complexity reduction of the implementation it makes sense to adapt the TC i.e. to add an extra bit in code word that contains an indication to encode the information or not according to the number of units in the input block.

• B.    Conversion combination MTF and Rice coding

MTF is a conversion to encode the data (usually a byte stream) designed to improve the performance of entropy coding. The basic idea is to replace each input symbol by its number in a special stack (register of recently used symbols) [9].

The sequences of identical symbols will be replaced by the original algorithm (starting with the second symbol) into a sequence of zeros. If the symbol does not appear in the input sequence for a long time it will be equal to a large number. The input symbols are replaced by a sequence of integers. If the input data have a lot of local correlations they are better for shifting that the original ones [10], [11].

Rice code is a family of binary prefix codes of natural numbers and zero representation. Codes differ by a single parameter k - number of bits allocated to the number mantissa. The method of encoding and decoding depends on the setting. So it should be known either by the transmitter or by the receiver.

The encoded number in binary notation is divided into two parts: k of the least significant bits and the rest of the k^th and high order. The high order part is encoded by the unary code and the least significant is recorded after the encoded high order part. For an n -block this code is given in ( n ⁄ m + k + 1) bits, where m = 2^k is a selected number that is a power of two [10].

As a result of simulation and testing of the developed devices the output file size and the duration of data processing were investigated. As TC parameters presence / absence of adaptation were used. In the presence of adaptation different minimum number of units was used. The test results were compiled in Tables

1 and 2 in which the following notation were agreed:

k min - minimum value.

C sh - the data shrinking coefficient.

t - number of tacts (millions).

KB - kilobyte.

TABLE.1 DEPENDENCE OF SHIFTING COEFFICIENT TC FROM VARIOUS PARAMETERS

n	t, mil tacts	Size, KB	Adaptation	k min	C sh
8	30,5	325	no	-	0,94
16	-	213	no	-	1,44
24	-	160	no	-	1,92
24	3,3	273	yes	2	1,12
	3,7	267	yes	3	1,14
	5,2	267	yes	4	1,14
	11,2	267	yes	5	1,14
	45,4	267	yes	6	1,14
32	3,2	268	yes	2	1,15
	3,5	264	yes	3	1,16
	5,2	262	yes	4	1,17
	15,5	260	yes	5	1,18
	60,1	259	yes	6	1,19
48	3,2	259	yes	3	1,19
	3,6	255	yes	4	1,20
	5,9	251	yes	5	1,22
	15,35	249	yes	6	1,23
64	80,5	254	yes	5	1,20
128	8,4	255	yes	4	1,20
256	12,6	256	yes	4	1,19
512	24,1	259	yes	4	1,18

TABLE.2 DEPENDENCE OF SHIFTING COEFFICIENT IN RICE CODING FROM VARIOUS PARAMETERS

k	2	3	4	5	6
C sh	0,50	0,78	0,98	1,11	1,09
Size, KB	612	392	302	275	281
t, mil tacts	1,8
MTF	no
k	2	3	4	5	6
C sh	0,73	1,04	1,21	1,21	1,12
Size, KB	415	295	254	254	274
t, mil tacts	23
MTF	yes

As a result TC shrinking method with the parameters mentioned above was chosen for the following reasons:

• •    TC processes an input block for less tacts.

• •    TC has a higher shrinking coefficient.

• •    For the TC implementation with the block length of 48 bits less memory is required.

The following variants of TC implementation are possible:

• •    The programmatic approach with the help of computer.

• •    Hardware-software method using single-board computer or computer on a single chip.

• •    Development of specialized devices on basis of the original chip using flash technology.

• C.    The proposed method of image shrinking

Taking into consideration the specificity of application the more promising is the third way of image shifting without loss. The proposed algorithm of image shrinking is based on above mentioned methods but with a number of modifications and adding. As a result of the procedure the images of that are transferred to a capsule are shrunk on 20%. The results are shown in Fig. 2.

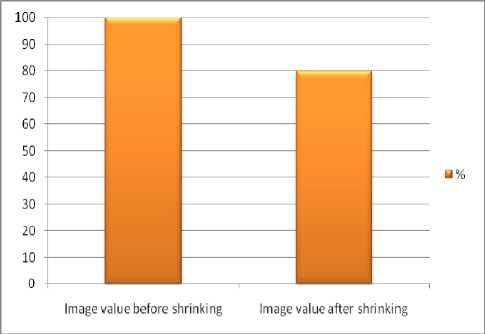
Figure 2. The results of image shrinking process.

The chip input receives binary sequence with the statistical redundancy and removed. From the output the sequence deprived of redundancy is received, i.e. data shifting is provided.

In Fig. 3 an algorithm implementing TC is shown. The following notations are agreed:

• •    k - the number of units in the original block;

• •    s - the sum number of units positions in the original block;

• •    b - the number of each particular code combination for fixed values of k and s ;

• •    N, K, S - the service parameters for the b- number calculation by the formula (2).

• •    r (n, k, s) - the number of binary combinations with k units and the sum of their position s in the n - bit block;

• •    A(I) – the one-dimensional array of bits of the analyzed input word;

• •    I - the current service index of units positions numbers.

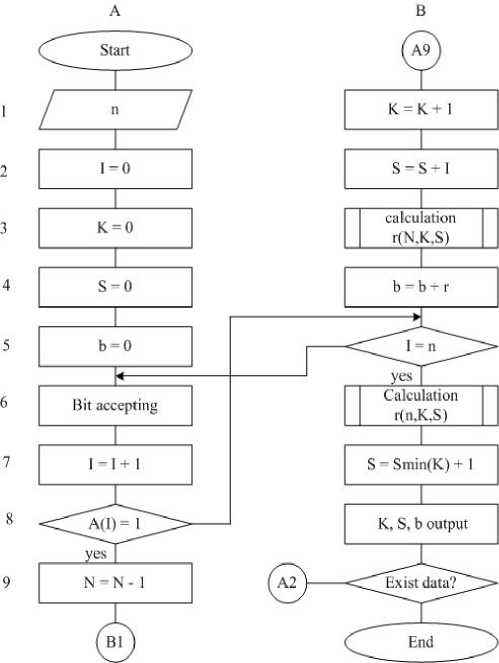
Figure. 3. Encoding algorithm.

The n value is considered to be given specified. It is the block length into which the original sequence of binary symbols is divided (block A1).

I is the number of processed n-block; k is current value of the number of units in the block; S is the sum of the numbers of their positions; b is the number calculated by the formula (2); A (I) is the contents of the Ith bit of n-block.

In blocks A2, A3, A4, A5 codeword parameters have initial values.

From the output of the channel the binary data are received. In block A6 the following bit of the sequence is transmitted. In block A7 the value of I is incremented by the unit.

In block A8 it is determined whether contents of the Ith bit of n-block is equal to unit. If "Yes" the corresponding items of formula (2) are calculated in the codeword (blocks A9, B1, 2, 3). In block B4 the calculated item is added to the current value of the number b.

If in block A8 it turns out that the contents of the Ith bit of n-block is equal to zero the process moves to block B5. It is revealed if all bits of n-block are checked. If "No" the process moves to block A6. If "Yes" in block B6 the sum of units’ positions of the original block is modified. The original value of S is replaced by its number.

In block B7 the coefficient needed to determine the number of bits required for the transmitted codeword number is calculated. In block B8 a generated codeword is provided. If the channel continues to receive data the process moves to block A2.

• IV. Conclusion

The wireless capsule endoscopy still faces the problem of image shrinking inside the capsule in order to get more data for analysis without increasing the size of the device.

The suggested method shrinks images received from an endoscopic capsule on 20% without any loss. The method is based on the research of existing methods of image shrinking advantages of which are used in proposed algorithm.

This method is complied with all the technical requirements made by the wireless capsule endoscope.

The shrinking of the transmitted information will increase image acquisition frequency reducing energy consumption. As a result endoscopic capsule may work for a longer period of time.

The proposed method of automatic image shrinking in the wireless capsule endoscopy will be improved and modified for better information compression.

In conjunction with the software installed on the receiver that automatically selects the images suitable for the research the developed method provides exhaustive information about gastrointestinal tract in a form suitable for analysis.

Acknowledgment

We would like to thank PhD in medical sciences, doctor of higher category of The Clinical Hospital № 85, Moscow, Russia Gubaidulina Landish Ildousovna for her inestimable contribution in this study.