General Research on Image Segmentation Algorithms

Published Online October 2009 in MECS

Image segmentation is the foundation of object recognition and computer vision. In order to comprehend image segmentation more deeply, some general knowledge of the structure of image segmentation system is presented first.

As is shown in figure 1, in general, image-noise should be eliminated through preprocessing before the main operation of image segmentation. And there is some specifically-given work (such as region extraction and image marking) to do after the main segmentation for the sake of better visual effect [1].

In image preprocessing, firstly, various color spaces should be transformed into specifically-given color space [3]. Then some techniques such as Gaussian filter are used to smooth images to diminish the influence of noise. As the main body of image segmentation system, image segmentation algorithm determines the result of image segmentation. After that, region merging and region extraction are used to combine unreasonably discontinuous regions. All the efforts above can ensure a satisfying image segmentation result.

Manuscript received January 13, 2009; revised June 22, 2009; accepted July 21, 2009.

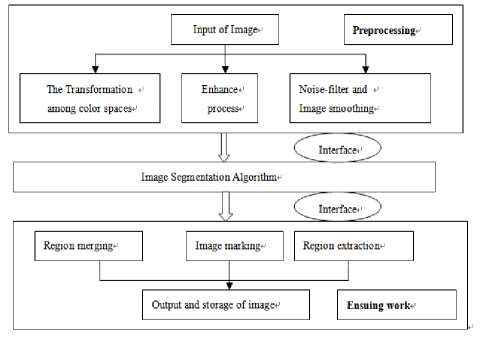
Figure 1. The Structure of Image Segmentation System [2]

In this paper, firstly, main image segmentation algorithms are classified and reviewed; then evaluation and comparison of image segmentation algorithms are discussed in depth based on the reason that evaluation of image segmentation is essential in the aspect of comparing the segmentation algorithm and providing advice for improvement.; at last, evaluation results of typical segmentation algorithms in MATLAB environment are summarized and presented.

• II.    Classification of image segmentation

ALGORITHMS

Image segmentation is generally defined as the basic image processing that subdivides a digital image f ( x , y ) into its continuous, disconnect and nonempty subset f ₁ , f ₂ , f ₃ , L f_n , which provides convenience to extraction of attribute [3]. In general, Image segmentation algorithms are based on two basic principles [4]: the trait of pixels and the information in nearby regions. Most of segmentation algorithms are based on two characters of pixels gray level: discontinuity around edges and similarity in the same region. As is shown in Table I, there are three main categories in image segmentation [5]: A. edge-based segmentation; B . region-based segmentation; C . special-

TABLE I.

C lassification of image segmentation

Main categories	Sub-classes		Interpretation
Edge-based segmentation	Gray-histogram technique		Partition an image through detecting edge among different regions.
	Gradient-based method	Differential coefficient technique
		Laplacian of a Gaussian(LoG)
		Canny technique
Region-based segmentation	Thresholding	Otsu	Exact the objects from the background by setting reasonable gray threshold Ts for image pixels.
		Optimal thresholding
		Thresholding image
	Region operating	Region growing	Partition an image into regions that are similar according to given criteria, such as gray character, color character or texture character and so on.
		Region splitting and merging
		Image matching
Special theory based segmentation	Fuzzy clustering segmentation		Introduce Fuzzy Set Theory into image segmentation
	Neural networks based segmentation		It is a learning algorithm imitating the working pattern of neural networks.
	Physically-based segmentation		Utilizing the physical characters of images to partition.

theory-based segmentation. And some sub-classes are included in the main categories too.

• III.    Edge-based segmentation

Understandably, an edge is a set of linked pixels lying on the boundary between different regions, where there are intense discontinuities such as gray change, color distinctness, texture variety and so on [6]. An image can be segmented by detecting those discontinuities. Based on this theory, there are two main edge-based segmentations methods: gray-histogram method and Gradient--based method.

The key to a satisfactory segmentation result lies in keeping a balance between detecting accuracy and noise immunity [7]. If the level of detecting accuracy is too high, noise may bring in fake edges which make the outline of images unreasonable; otherwise, some parts of image outline may get undetected and the position of objects may be mistaken if the degree of noise immunity is excessive.

A.    Gray-histogram technique [8]

In order to detect the edge of an image, gray-histogram of the image is divided into two parts using threshold T . Then operations on the image f(i,j) are processed as follows: (1) scanning every row in image f(i,j) , and comparing gray value of every pixel in the row with T , which results in image g 1 (i,j) ; (2) scanning every column in image f(i,j) , and comparing gray value of every pixel in the column with T , which results in image g 2 (i, j) ; (3) incorporating image g 1 (i, j) and g 2 (i,j) to get edge image g(i, j) .

In the process above, the quality of edge detection depends greatly on the fitness of threshold T. However, it is really difficult to search for the maximum and minimum gray value, because gray-histogram is uneven for the impact of noise. In this case, we can approximatively substitute the curves of object and background with two conic Gaussian curves, whose intersection is the valley of histogram. Threshold T is the gray value of the point at the valley.

B.    Gradient-based method

Gradient is first derivative for image f(x, y). When the change of gray value near edge is intense enough and there is little noise in the image, Gradient-based method works well, and segmentation result is adaptive to the direction of gradient. There are three most commonly used Gradient-based methods: differential coefficient technique, Laplacian of Gaussian (LoG), and Canny technique. Among them Canny technique is the most representative one. Canny firstly proposed three criteria for edge detection: optimal detection result, optimal position outcome, and low repeating response [3]. Based on these criteria, he invented “optimal linear filter”, which is first derivative of Gaussian function [3]. The basic idea of Canny technique is as much as follows: firstly filter image f(x, y) with Gaussian function to get smooth image f(x, y)*Ga(x, y). (a stands for scale coefficient), then find the edge pixels by calculating the magnitude of gradient, denoted Ma, and the direction of gradient, denoted Aa. The edge points of the image are the points having the maximum of Ma in the direction of Aa. Equation (1) is the mathematics’ expression of this method.

f M _a =\\ f ( x , y )* V G _a ( x , y )||

A _a

f ( x , y )* V G _a ( x , y ) || f ( x , y )* V G _a ( x , y )||

However, as the magnitude of gradient is carried out by finding out the zero points of second derivative, those zero points may be both the maximum and minimum of the first derivative. So that the pixels whose gray values change intensely as well as the pixels whose gray values change slowly can be detected equally. Accordingly, it is obvious that Canny technique may bring in fake edge points.

• IV.    Region-based segmentation

Edge-based segmentation partitions an image based on abrupt changes in intensity near the edges whereas regionbased segmentation partitions an image into regions that are similar according to a set of predefined criteria. Thresholding, region growing, region splitting and merging are the main examples of techniques in this category [10].

A.    Thresholding Methods

Thresholding techniques are image segmentations based on image-space regions. The fundamental principle of thresholding techniques is based on the characteristics of the image [11]. It chooses proper thresholds T_n to divide image pixels into several classes and separate the objects from background. When there is only a single threshold T , any point ( x , y ) for which f ( x,y ) > T is called an object point; and a point ( x , y ) is called a background point if f ( x, y) <  T .

According to the aforementioned discussion, thresholding can be viewed as an operation to gain threshold T in the following equation:

T = M [ x , y , p ( x , y ), f ( x , y )] ^{( 2 )}

In (2), T stands for the threshold; f ( x , y ) is the gray value of point ( x , y ) and p ( x , y ) denotes some local property of the point—such as the average gray value of the neighborhood centered on point ( x , y ) . Based on (1), thresholding techniques can be mainly divided into global, local, and dynamic thresholding techniques.

• 1)    Global thresholding: When T depends only on f ( x , y ) (in other words, only on gray-level values) and the value of T solely relates to the character of pixels, this thresholding technique is called global thresholding technique [5]. There are a number of global thresholding techniques such as: minimum thresholding, Otsu, optimal thresholding, histogram concave analysis, iterative thresholding, entropybased thresholding, MoM-keeping thresholding and so on.

Minimum thresholding: For simple images, the object and background can be seen clearly in different gray levels. Obviously, in this case, the proper threshold T is the gray value of the valley point between two separate wave crests in image histogram. The problem of searching for the valley of image histogram can be transformed into the task of seeking for the minimum in peripheral curve ^{L ( z )} . Based on the extremum knowledge gained from Advanced

z

Mathematics, we get the minimum gray value ⁰ by equating the first and second derivative of L(z) with zero. And z0 is the threshold ^T . The original image should be smoothened beforehand and the noise in the image should be removed too. Minimum-based thresholding can give birth to satisfying image segmentation if the gray value of object is quite different from the background; otherwise, its segmentation can be unfavorable.

Otsu: From the viewpoint of pattern recognization, thresholdT should be the value that results in the optimal segmentation performance between the object and the background. That is to say, suppose a thresholdT partitions an image into two parts: f1 and f2 , and the optimal T should leads to a maximal mean square cr 2 (T )

error . Based on this principle, the optimal threshold ^T can be calculated. Otsu thresholding is simple, stable and is used broadly.

• 2)    Local thresholding: If threshold T depends on both f ( x , y ) and p ( x , y ) , this thresholding is called local thresholding [5]. This method divides an original image into several sub regions, and chooses various thresholds Ts for each sub region reasonably. After thresholding, discontinuous gray levels among sub images must be eliminated by gray level filtering technique. Main local thresholding techniques are simple statistical thresholding, 2-D entropy-based thresholding, histogram-transformation thresholding etc.

Simple statistical thresholding: Simple statistical thresholding acquires threshold T by pure mathematics equations. Thereby, we can avoid the analysis of histogram, letting alone optimizing function [5]. The equations are shown as follows:

e x = f ^{( x -} 1, y ) - f ^{( x} + 1, y )

e y = f ^{( x} , y ^{- 1 )-} f ^{( x} , y + 1 )

e ( ^x , y ) = max { e x |, e y 1}

E E e ^{( x} ■ y ) ^{f ( x} ■ y ) xy

E E e ( x , y )

^xy                      (3)

In (3), e(x, y) stands for the neighborhood character of point (x, y) . So it is clear that this segmentation is a kind of local thresholding.

2-D entropy-based thresholding: In 1989, Arutaleb combined one-dimension maximum entropy method with 2-D thresholding proposed by Kirby and his fellows, and invented 2-D entropy-based thresholding. This thresholding uses gray level and local mean gray value (LMGV) to form 2-D gray histogram to choose suitable threshold T .

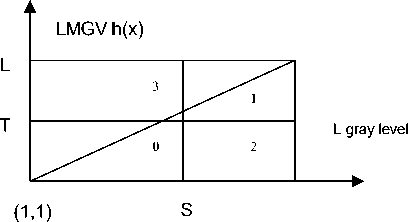
Figure 2. 2-D gray histogram

As is shown in Figure 2, in the area 0 and 1, the gray level of pixels is similar to LMGV h(z), which reveals strong consistency. In this light, those two areas generally belong to object or background regions. With the same logic, area 2 and 3 should be deemed as noise or edge for their weak consistency. 2-D entropy-based thresholding realizes image segmentation by choosing a couple of numerical value(S, T), which maximizes the subsequent entropy between object and background.

• 3)    Dynamic thresholding: If, in an image, there are several objects taking up different gray level regions, the image should be partitioned with vary dynamic thresholds ( T 1 、 T 2 、 …T n ) [5] , depending on f ( x , y ), p(x, y) and the spatial

coordinates x and y. In general, dynamic thresholding techniques include Thresholding Image, Watershed, interpolatory thresholding and so on.

Thresholding image: The aim of thresholding image, is to create a image B(x,y) with the same size of original image A(x,y) by means of increasing the threshold number until it reaches the pixel number in A(x,y). For example, the thresholding image B(x, y) can be formed in this way: Firstly, initialize every pixel in B(x, y) with zero; then, calculate the mean gray value T0 of original image within a smooth n×n (the value n is alterable) template, and endue the center point of the template of image B(x, y) with the mean gray value (B(x, y)= T0). Orderly, move the mask from the left- below point in original image to its right-above point and calculate all the gray values in thresholding image B(x, y).

Then, segmentation of original image can be processed by the following equation:

' A(x, y) = 0

<

[ A ( x, y) = 255;

if A(x, y) >  B(x, y) if A ( x, y ) <  B ( x, y)

Segmentation experiment shows that the segmentation result of this method is good enough. Using noise filter, the result can be even better. However, thresholding image technique indeed has its drawback too: the information near image outline may get lost.

Watershed: An image can be visualized in three dimensions: two spatial coordinates versus gray levels. Based on such a morphological concept, there are three basic types of points [4]: (1) points that fall into a regional minimum; (2) points where if a drop of water is placed at the any location of those points it would invariably fall to a single minimum; (3) points where water would equally fall to more than one such minimum. For a certain regional minimum, the set of points satisfying condition (2) is titled the catchment basin or watershed of that minimum. And the points satisfying condition (3) form crest lines on the morphological surface are called divide lines or watershed lines.

From all the discussion above, it is clear that the chief objective of this segmentation algorithm is to find the watershed lines. The commonly used way is simple: Assume that a hole is dug in each regional minimum and that the entire topography is flooded from below by letting water rise through the holes at an uniform rate. When the rising water in different catchment basins is about to merge, we built a dam to prevent it. As this process goes on, the topography will eventually reach a state that only the tops of the dams are visible above the water line. These dam’s boundaries are the edges extracted by watershed segmentation algorithm.

Watershed segmentation is simple and works well in extracting the outline of the original image. However, as it needs gradient information, the noise in original image will lead to lots of fake regional minimums, which ultimately will result in over-segmentation.

• 4)    Other improved thresholding segmentation algorithms: As thresholding is a basic technique of image segmentation, much attention is given to improve thresholding algorithms. As a result, many new improved thresholding algorithms come into being day in and day out. Considering that traditional Otsu is overly sensitive to the proportion of object and background, literature [10] proposed the Fisher Criterion Function Method. This method is less affected by the object’s size and it has a quite stable segmentation performance as well as a fast computing speed.

Relaxation-based segmentation [5] improves the convergent trait of linear equations system by iteratively using local restriction terms. The process of this method is like this: Firstly, divide all the pixels into two types—bright and dark regions according to the probability of gray levels. Then, adjust the probability of every pixel according to the probability of pixels in neighborhood and repeat this adjusting until optimal segmentation result is attained.