Generalized Algorithm on idiosyncrasy of Numbers

In mathematics, enthusiasm and determination are amusing and entertaining. The science of numbers has a natural attraction from the commencement of studentship. Numbers are an extremely important constituent of mathematics, especially in number theory. Every individual expresses the inclination and desire to identify, enumerate, discrepancy, resemblance, summarize, classify and generalize the numbers.

Since 1949, Kaprekar’s constant (6174 and 495) continues to attract mathematicians and science scholars even after many decades. Kaprekar [1, 2] discovered an exciting and miraculous process, known as Kaprekar’s operation, wherein considering any four or three-digit numbers (all digits are not repeated), it reaches 6174 and 495 in at the most seven and six steps respectively. Many researchers [3, 4, 5, 6, 7, 8] studied problems related to this process and intriguing questions linked with it.

Verma [9] studied the weirdness of numbers, Yutaka Nishiyama [10] and Naranan [11] have labeled that the number 6174 is really a mysterious number. Patil and Shah [12] derived the Kaprekar’s number and its analog equations. A variation on the two-digit kaprekar routine is studied by Anne Ludington Young [3]. Researchers [4, 5, 6, 7, 8] also studied the above process and discussed many fascinating problems with this process.

In this paper, using a computer algebra system, a generalized algorithm is developed to demonstrate these operations for any n-digit number, which can be tested for an unrestricted number of iterations. Properties of the results obtained consisting of 2-digit, 3-digits. Digit numbers are studied and compared with the available results in the literature. Frequency and numbers of iterations table-1 is also worked out for all the 4-digits using this generalized algorithm which agree with the previous existing results. Using this algorithm, all 2-digit numbers are considered and discussed in detail in table-2 using this algorithm. It is observed that for 2-digit numbers divided into (excluding repeated digits) a 9-looping pattern which classifies these numbers into nine classes, each has nine numbers. Further, results obtained analytically are also exhibited graphically. Similar discussion can be made on all about other numbers using this algorithm.

2.    The Generalized Process

Following Kaprekar’s algorithm consider any number with n-digits ( n ≥ 2), where all the digits should not be same (i.e. other than 111. . . 1, 222. . . 2, . . . 999. . . 9). Firstly reshuffle and arrange the digits in decreasing and increasing order to get the largest and smallest numbers.

• •    If a number say is 5, and to use the generalized algorithm with 11-digits numbers then write this 5 as 00000000005 to make it a 11-digits number. (i.e. zeros must be embedded in the left side of minimum number to make it desired digits number before applying the algorithm with the largest and smallest numbers.)

• •    If a number is not equal to the desired n-digits ( n ≥ 2), then to make it n-digits ( n ≥ 2) number, zeros must be embedded in the left side of minimum number to obtain the largest and smallest numbers to make desired number.

• •    Subtract smallest number from the largest number.

• •    Carry on repeating the above procedure for each new number obtained and observe the output.

• 2.1    Algorithm for four digits numbers

  For any 4-digits number other than 1111, 2222 .......... 9999, arrange the digits of the number in descending and

  ascending order. Consider their difference; add leading 0’s to make it a 4 digit number if the resulting number is less than of 4 digits. Repeat the above steps till reaches 6174, a static point. The pictorial and analytical illustrations are presented in the “Fig. 1, and Fig 2” for 4-digits number.

Illustration 1: N = 2023

3220-0223 = 2997

8872-2799 = 7173

7731-1377 = 6354

6543-3456 = 3087

8730-0378 = 8352

8532-2358 = 6174

7641-1467 = 6174.

Interestingly it took six iterations to converge 6174. We stop here as all subsequent steps will only give 6174. 6174 is the end-point of our calculation. A fter reaching at 6174 it creates an infinite loop on the constant 6174. It is called a stable point.

Illustration 2: N= 9231

9321 - 1239 = 8082

8820 - 0288 = 8532

8532 - 2358 = 6174

7641 - 1467 = 6174.

Clearly three iterations required to converge 6174 and to repeats it.

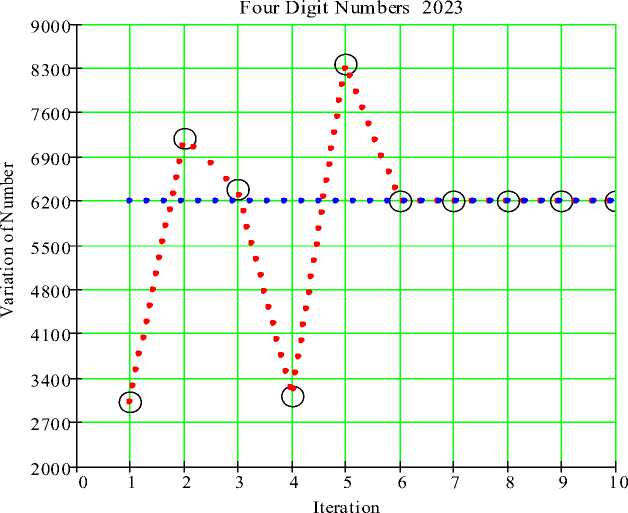
Fig. 1. Kaprekar’s operation on number 2023 with iteration.

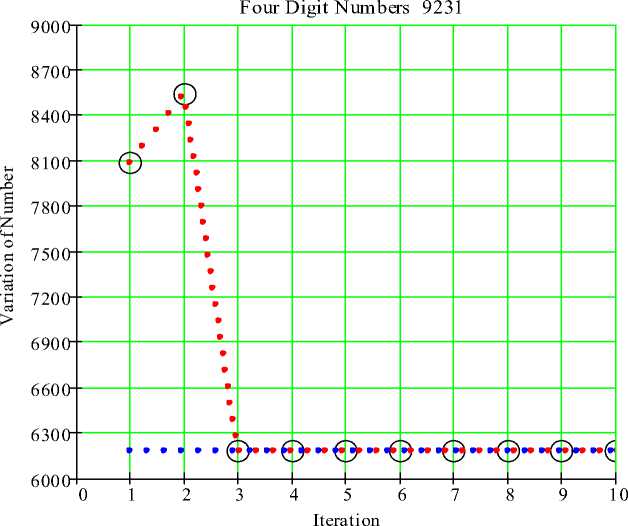
Fig. 2. Kaprekar’s operation on number 9231 with iteration.

The number 3358 takes 7 steps to reach 6174; the outcomes of consecutive subtractions are:

3358 →5175→5994→5355→1998→8082→8532→6174.

• 2.2.    Frequency and Number of iterations of 4-digits numbers converges to constant

  Researchers have developed algorithm on the Kaprekar’s process to work out for all the 4-digits from 0001 to 9998 (others than nine numbers 1111to 9999). In reference [10] researcher have checked all 4-digits left over 8991 numbers and found that every four digit number converges to 6174 in at most seven steps. Using this generalized computer algebra system algorithm on checking all 4-digits numbers output is presented in table-1.

• 2.3.    Algorithm for Three Digits Numbers

Table 1.

Number of iterations	0	1	2	3	4	5	6	7
Frequency	1	356	519	2124	1124	1379	1508	1980

On considering any three digit numbers not all the digits are same, the identical phenomenon occurs as in the 4-digits number. In this case the process converges to the number 495 and in no more than 6 iterations.

For example applying Kaprekar's operation to the three digit number 768 gives the following: 768 → 198 → 792 → 693 → 594 → 495.

The number 768 takes 5 steps to reach 495.

Similarly considering three digit number 101 gives the following: 101 → 099 → 891 → 792 → 693 → 594 → 495.

Thus the number 101 takes 6 steps to reach 495. Thus the number 495 is the unique kernel for the operation on three digit numbers, and all three digit numbers reach 495 using this operation. The pictorial and analytical illustrations are presented in the “Fig. 3, and Fig 4” for 3-digits number.

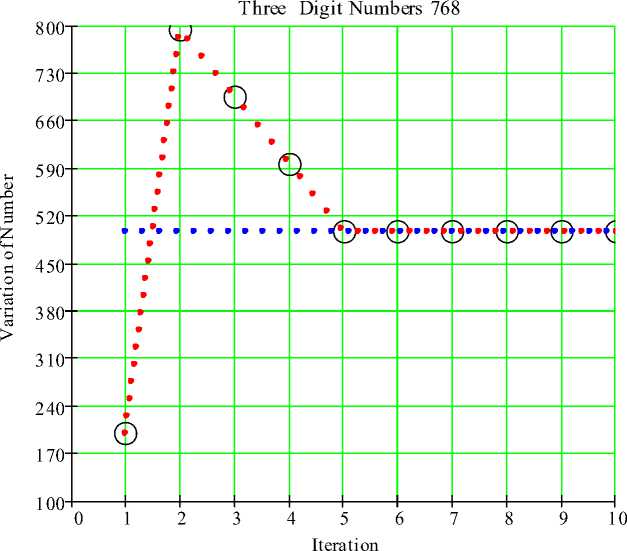
Fig. 3. Kaprekar’s operation on number 3-digit 768 with iteration.

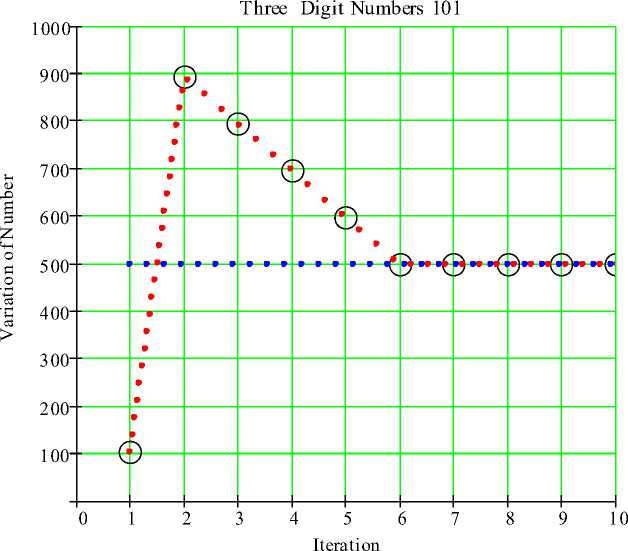
Fig.4. Kaprekar’s operation on number 3-digit 101 with iteration.

• 2.4.    Algorithm for eight-Digits Numbers

3.    Two Digits numbers

• 3.1.    Kaprekar operation on two digits number

Since there are unique kernels for 3 and 4 digits numbers. Algorithm is used to check what happens for number having n-digits (n ≥ 5), and output becomes extremely monotonous, and found that there is no kernel for 1-digit, 2-digits, 5-digits, 7-digit ...... numbers whereas there are two kernels for 6-digits, 8-digits, 9-digit ...... whereas it is found that 10-digits numbers having kernels, which is in agreement with algorithm by Yutaka Nishiyama [10]. A pictorial illustrations are presented in the “Fig. 5” for 8-digits number.

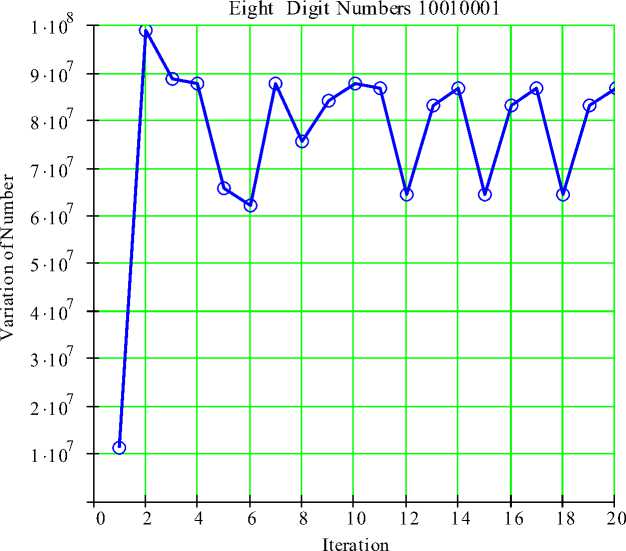
Fig. 5. Kaprekar’s operation on 8-digit number 10010001.

On attempting the algorithm for two digits numbers, unlike for three and four digits numbers, there is no unique kernel for two digit numbers. Outcome is given in the following table:

For all numbers 01-98 except where the digits are same (that is not 11, 22„...,99). Using the algorithm on checking all 2-digits numbers output is presented in table-2.

Table 2.

Loops Pattern	Number (01-98) except where the digits are same
{9,81,63,27,45}	01	12 10	23 21	34 32	45 43	56 54	67 65	78 76	89 87	98
{18,63,27,45,9,81}	02	13	20, 24	31,35	42,46	53,57	64,68	75,79	86	97
{27,45,9,81,63}	03	14	25	30,36	41,47	52,58	63,69	74	85	96
{36,27,45,9,81,63 }	04	15	26	37	40,48	51,59	62	73	84	95
{45,9,81,63,27}	05	16	27	38	49	50	61	72	83	94
{54,9,81,63,27,45}	06	17	28	39			60	71	82	93
{63,27,45,9,81}	07	18	29					70	81	92
{72,27,45,9,81,63}	08	19							80	91
{81,63,27,45,9}	09									90

In Table 2 all 2-digits numbers 01-98 except where the digits are same (that is 11, 22„...,99) are considered and algorithm is used for Kaprekar’s operation . It is observed that there are 9-looping patterns 5 patterns having the same 5 digits and 4 patterns having 6 digits with one new member. Interestingly, in each 6 digits pattern a new two digits appear. Corresponding to each loop, all two digits numbers (01 to 98) except where the digits are same are classified into 10 (columns) classes, each class have even numbers from 18 to 2 (top to bottom). In each patterns, sum of all the digits in each pattern is congruence (mod9).

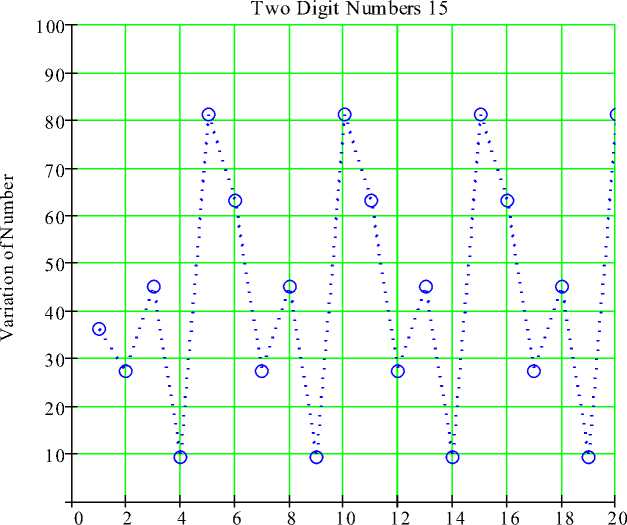
Fig. 6. Kaprekar’s operation on number 2-digit 15 with 20 iterations and the 6-digit loop is {36,27,45,9,81,63 }

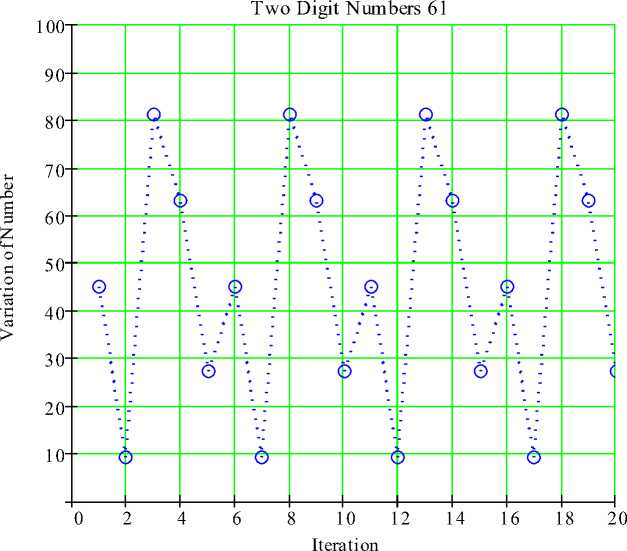
Fig. 7. Kaprekar’s operation on number 2-digit 61 with 20 iterations and 5-digit Loop is {45,9,81,63,27}.

4.    Conclusions

Using computer algebra system in symbolic form, a symbolic program is written to explore the Kaprekar’s operation for n-digits (n ≥ 2) to study and display the results graphically. “Figs 1-2” exhibit the obtained results for 4-digits numbers. Frequency and numbers of iterations is also worked out for all the 4-digits using this generalized algorithm which agrees with the previous existing results is shown in table-1. Similarly, “Figs.3-4” display the results for 3-digits numbers. “Figs. 6-7” Demonstrate the results obtained for 2-digits numbers and the results obtained analytically are shown in Table-2. For 8-digits numbers graph obtained are exhibited in Fig. 5. It is found that using this algorithm for Kaprekar's operation every 3-digits and 4-digits (non-repetitive) numbers converge to a unique kernel, whereas this operation for 2-digits numbers form patterns in 9 loops. Among them 5 loops have the same numbers with different order. All the 2-digit 91 numbers are classified into 9 classes exhibited in table-2. Further, for any 2-digit numbers and on reversing the order of digits has the same representation. it is also true for any n-digits (n ≥ 2) numbers. It is also observed from Table-2 and figure 6 and “Fig. 7”, that numbers which are congruent to ±2, ±4, ±6, ±8 show extra two-digit number at the beginning before settling for a repeated sequence. The numbers preceding and succeeding (11, 22, ... , 99) also have the same representation and lies in the first row of Table-2 against first pattern. Sum of digits of any numbers in all nine patterns is 9. Interestingly non-repeating two-digit numbers 18, 36, 54 and 72 in second, fourth, sixth and eighth patterns congruent 9 with 2, 4, 6 and 8 as quotients. Any two-digit number, if the sum is not 9 then it is not part of any pattern. The numbers in a row against jth pattern are congruent to ±j (modulo 11), j =1, 2, . . . 9. Variation of 6-digits number such as 10010001 up to 20 iterations using Kaprekar’s operation is exhibited in Figure 7. Various progresses in science and Mathematics have been driven by ‘mistakes’. Mathematicians, all over the world are still working where some great theory of mathematics might lie behind such processes. The advantages of generalized algorithm developed using the computer algebra system in this paper is that considering n-digits (n ≥ 2) number and employing the algorithm for Kaprekar’s procedure, we obtain results for any n-digits number. The validity of relevant results discussed and obtained can be easily verified using this algorithm.