Generalized Galois-Fibonacci Matrix Generators Pseudo-Random Sequences

In the theory and practice of cryptographic information protection, one of the critical problems is constructing generators of pseudo-random numbers (PRN) of the maximum length (period) with good statistical properties . There are two main PRN generators (PRNG), which built using: (1) hardware and (2) software. The first class of generators usually made based on linear feedback shift registers (LFSR) in Galois or Fibonacci configurations (according to schemes) [1-6]. Structural and logical diagrams of classical LFSR generators uniquely determined by generating primitive polynomials (PP), using single-loop feedbacks established in shift registers [3,7]. The software-implemented PRNG, which makes up the second class of generators, can also be built based on LFSR.

This article focuses on constructing generalized matrix PRNG in Galois and Fibonacci configurations [8-10]. The terms of the Galois matrix G and those bijectively associated with them by the operator of the right-hand transposition (i.e., transposition to the auxiliary diagonal [11]) of the Fibonacci matrix F borrowed from the theory of cryptography [1,3]. The Galois and Fibonacci matrices will be called PRNG.

In addition to the named base (initial) matrices G and F the so-called conjugate matrices G * and F * are introduced in work, which is formed by the classical (left-sided) transposition to the main diagonal of the corresponding initial matrices. The set of matrices { Q } = { G , F , G * , F * } , where this does not lead to ambiguity, will be called "Galois matrices" for simplicity. All Galois matrices of the scene can be obtained by linear transformations of the left-sided and right-sided transposition (in the latter case, the transposition to the auxiliary diagonal) of the Frobenius normal form [12]

ф

n

1   0  ...  0

0   1   ...  0

0   0   ...   1   - cn—i called in linear algebra the accompanying matrix of the unitary polynomial

Ф _n ( x ) = x" + c n - x^{n - 1} + ...+ c k x^k. ..+ c₁ x ¹ + c ₀,   c k e GF ( p )

The possibilities of using Frobenius matrices (1) for constructing PRNG based on the following properties Ф . First, if as a polynomial ф„ ( x ) we choose a unitary irreducible polynomial f_n , represented by its vector form (a set of polynomial coefficients), i.e.

V n (x) ^ fn = 1an-1«n - 2-"«Г ••«1«0,  “k = (- ck )mod P, then the matrix Ф goes into the Fibonacci matrix

	"0	0	0	a 0
	1	0	0	« 1
F n =	0	1	0	аг
	0	0	1	« n - 1

And secondly, matrix (2) generates a linear recurrent m -sequence a ₀, a , • ac_k ,... by transforming

p

(ak ak+1 • • • ak+(n-1) ) ® Fn = ak+1 ak+2 • • • ak+(n-1) ak+n for all k > 0.

Let's pay attention to this feature of recursion (3). All high-order elements ^ +1 ^ +2 • • a^,^ of the output vector V_out are contained in the set of known components of the input vector V_n = qa • • a_k^_n __n . The only unknown part a_k+n of the vector V _out determined, according to relations (2) and (3), by the scalar product of vectors V_m and A = ^a 0 « 1- .. « k.      - 2 «n - 1 , i.e.

« k + n = ⁽ « k « 0 ⁺ « k + 1 « 1 +••• + « k + n - 1 « n - 1 ) ^mod P                                 ⁽⁴⁾

The process of calculating a sequence of vectors V will illustrate the fourth-order Fibonacci matrix F generated by the binary PP f = 10011.

As the initialization vector, let us designate it as V _n , on the left side of expression (3), you can choose any nonzero binary vector of the fourth-order. Let this be the vector V = 1011. The results of calculating the recursive sequence by formulas (3) - (5) for the selected parameters of the vectors are summarized in Table 1.

Table 1. The sequence of the state of the Fibonacci PRNG generated PP f = 1'0011

Step ( k )	The elements of V					Step ( k )	The elements of V
	0	1	2	3			0	1	2	3
0	1	1	0	1		8	1	0	0	0
1	1	0	1	0		9	0	0	0	1
2	0	1	0	1		10	0	0	1	0
3	1	0	1	1		11	0	1	0	0
4	0	1	1	1		12	1	0	0	1
5	1	1	1	1		13	0	0	1	1
6	1	1	1	0		14	0	1	1	0
7	1	1	0	0		15	1	1	0	1

Shading in the Table. 1, the vector is selected, which coincides with the initialization vector. The number of nonrepeating non-zero vectors generated by the Fibonacci generator turned out to be 15, as it should be for the selected parameters of the generation.

Up to now, matrix PRNG has not yet received widespread use in cryptography. Classic matrix ones often do not provide the required level of cryptographic strength. The notable drawback is that the Berlekamp-Messi (BM) algorithm [13, 14] allows unambiguously determining the primitive polynomial generating the generator matrix, using the 2 n output serial bits of the PRNG. And, as a result, the generator is hacked.

The main task of this study is to develop matrix generators of pseudo-random sequences of numbers of the maximum period based on generalized Galois matrices (in the general case over fields of arbitrary characteristics) free from the Berlekamp-Messi attack.

• 2.    Classical Hardware and Matrix PRNG According to the Galois and Fibonacci Schemes

Definition 1. Generators built based on linear shift registers with single-loop feedback exclusively function as a primitive generating polynomial called classical PRNG.

D -flip-flops are usually used as LFSR bits, which rewrite the input signal to the trigger output when the sync pulse arrives. An example of a fourth-order Galois generator, in which a fourth-degree PP f = 1'0011 forms feedbacks, is shown in Fig. 1

Fig.1. Structural logic diagram of the PRNG in the Galois configuration generated by PP f = 10011

Using Fig. 1, we will develop a mnemonic rule according to which structural diagrams of classical LFSR generators in the Galois configuration are drawn up. For this purpose, we will supplement the drawing with dotted strokes, placing them on those parts of the circuit in which there are no XOR operators. Then we put down numbers 1 above the solid vertical lines (feedback lines) and numbers 0 above the dashed lines. We come to fig. 2, which coincides with Fig. 1.

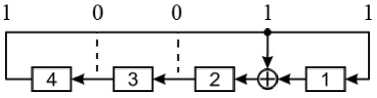
Fig.2. To build a block diagram fourth-order Galois generator

As follows from Fig. 2, the ones of the primitive polynomial in vector form predetermine the position of the vertical lines in a single-loop feedback circuit in the classical LFSR Galois PRNG.

The technology of applying formulated rules for drawing up a structural diagram of the PRNG of the maximum period in the Galois configuration will be illustrated by constructing a generator circuit generated by a PP of the eighth degree f = 101100101 . The solution to this problem involves the implementation of these two stages of synthesis.

Stage 1 . Form an eight-bit ring shift register (Fig. 3), in the nodes of the feedback line of which we equidistantly arrange the coefficients of the selected primitive polynomial

1  0  110  0  10  1

Fig.3. To the construction of an eight-bit Galois generator circuit

Stage 2 . Connecting, as shown in Fig. 4, the internal nodes of the feedback line, above which there are coefficients 1, with the XOR operator, we complete the construction of the classical LFSR Galois generator.

Fig.4. Block diagram of the Galois generator, generated PP f = 101100101

Similarly, by the above steps 1 and 2, it is possible to construct the structural logic circuits of the classical LFSR generators in the Galois configuration for an arbitrary degree of the primitive polynomial that forms a feedback loop in the generator register.

According to the Galois scheme and classical LFSR generators, generators in the Fibonacci configuration widely used in cryptography. Such generators are formed from Galois generators due to a 180 ° rotation of the feedback loop relative to both the vertical and horizontal axes while maintaining the numbering of the shift register cells without changing (Fig. 5).

Fig.5. Block diagram of the Fibonacci generator, generated PP f = 101100101

According to the Galois or Fibonacci scheme, each LFSR generator corresponds to matrices uniquely associated with them, which we will denote as the symbols G and F . A distinctive feature of the Galois and Fibonacci matrices is that it is possible to generate binary series similar to the m — sequences formed by the classical LFSR generators on their basis.

Let be S ( k ) — the state vector of the PRN n — discharge generator in the Galois configuration, generated by the PP f , after the k — th sync pulse (at the k — th step of the register shift), the calculation scheme of which is represented by the matrix expression

S ( k + 1) = S ( k ) • G ⁽_zn ) , k = 0,1,..., S (0) = 00...01. (6) n bit

Our task is to calculate the Galois matrix for a given PP f = 1а_я-1а_п_₂.. a_k. . .a _t1, a_k e GF (2) = { 0,1 } , with the help of which relation (6) forms the same sequence of pseudo-random numbers as the LFSR generator. Let us try first to deal with this problem for small orders of matrices. Let us turn to the analysis of the state of the triggers of the PRNG (Fig. 6), previously shown in Fig. 1.

Fig.6. Initial state illustration Generator PRN according to Galois scheme

The numbers placed above the generator bits characterize the logic level of the signal at the output of the corresponding cell (trigger) of the register. As shown in Fig. 7, using sync pulses, 1 from the least significant bit of the register moved to its most significant bits.

From Fig. 7, it follows that after the third synchrotact, logical ones arrive at the inputs of both the first and second flip-flops and, therefore, at the fourth step of the PRN generation (Fig. 8) appear at the outputs of these triggers.

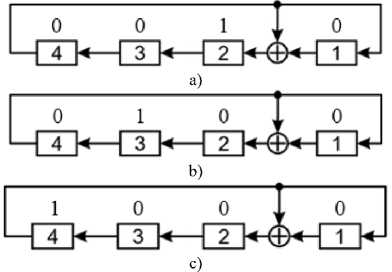
Fig.7. PRNG states after: a) - the first, b) - the second, c) - the third synchro tact

Fig.8. State of the PRNG after the fourth synchro title

Let us compose a matrix G ⁽⁴⁾ from a set of state vectors S ( k ), into which the Galois generator passes after the first four synchronizations, placing the vectors in the matrix, starting from its bottom row i = 1.

T i

	' 0	0	1	1 ^	4
(4) G 13   =	1 0	0 1	0 0	0 0	3 . 2
	1 0	0	1	0 >	1
^ J	4	3	2	1

Note that index 13 in the notation of the matrix G ^{( n )} in (7) is nothing more than the hexadecimal notation of PP f = 1'0011. We will use the exact representation of the numerical values of the degree of polynomials in the future.

At first, it is easy to verify that the matrix rows (7) constitute a set of linearly independent vectors, due to which the matrix G ⁽⁴⁾ turns out to be nondegenerate. Second, the matrix G ⁽⁴⁾ , which is substituted into equation (6), forms a sequence of four-bit codes (Table 2), a multiplicative group GF * (2 4 ) of the field generated by the PP f = 1'0011.

Table 2. The sequence of the state of the PRNG generated PP f = 1'0011

Step ( k )	LRS discharges					Step ( k )	LRS discharges
	4	3	2	1			4	3	2	1
0	0	0	0	1		8	0	1	0	1
1	0	0	1	0		9	1	0	1	0
2	0	1	0	0		10	0	1	1	1
3	1	0	0	0		11	1	1	1	0
4	0	0	1	1		12	1	1	1	1
5	0	1	1	0		13	1	1	0	1
6	1	1	0	0		14	1	0	0	1
7	1	0	1	1		15	0	0	0	1

Third, the top row of the matrix (7) is nothing but the fourth degree PP f = 1'0011, in which the leading unit is removed, and the leading (left) element of the truncated polynomial is the coefficient а_н j.

Based on the analysis of the matrix G ⁽⁴⁾ in (7), we arrive at the following construction rule (synthesis algorithm) of the classical Galois matrix (CGM) G ^{( n )} of the order n generated by a primitive polynomial f of degree n .

Algorithm for the synthesis of CGM: let f - a primitive binary polynomial of degree n and 6 = 10 - the minimal primitive element of the field GF(2n), generated by the polynomial. Place 6 in the lower right corner of the generated Galois matrix G (nn). All other digits of the bottom line G (nn), located to the left of the element 0 , are filled with zeros. Suppose the stage of formation of the next row its senior 1 goes beyond the left boundary of the matrix. In that case, the polynomial located in this row is reduced to the remainder modulo f . Thus, the row returns to the matrix, and the formation process of G (n) continues further.

The right-hand side of matrix (2) can represent in a more compact form.

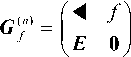
where E - the identity matrix of the ( n - 1) - order, the 0 — zero column vector of length, and the pointer of the position of the highest PP coefficient a k .

	(a    1 n - 1	a n - 2	a     о • • n - 3	a 2	a 1	1 )	n
	1	0	0	0	0	0	n - 1
G (nn ) =	0	1	0	0	0	0	n - 2 3
	0	0	0	0	0	0
	0	0	0	1	0	0	2
	V 0	0	0	0	1	0 V	1
	n	n - 1	n -2   •••	3	2	1

In matrix (9), for clarity, the elements of the main diagonal of the identity matrix E and the bordering elements of this matrix are highlighted in bold (on the right – the zero column 0 , and on top – the row, which is a primitive polynomial f shortened by one digit on the left, generating the CGM G ^{( n )} ).

Compact forms of Fibonacci matrices F ^{( n )} are interconnected with Galois matrices G ^{( n )} in configuration (8) by the operator of right-hand transposition [11].

_G ( n )

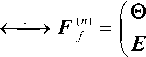
where 0 — is the zero-row vector of the ( n - 1) - order.

For example, let us give expressions for the matrices and generated by the PP. Structural logic diagrams of Galois and Fibonacci LFSR generators, corresponding to relations (11), are shown above in Fig. 4 and 5, respectively

	^ 0	1	1	0	0	1	0	1 "	i 8	^ 0	0	0	0	0	0	0	1 "	i 8
	1	0	0	0	0	0	0	0	7	1	0	0	0	0	0	0	0	7
	0	1	0	0	0	0	0	0	6	0	1	0	0	0	0	0	1	6
G =	0 0	0 0	1 0	0 1	0 0	0 0	0 0	0 0	5 F = 4	0 0	0 0	1 0	0 1	0 0	0 0	0 0	0 0	5 4	(11)
	0	0	0	0	1	0	0	0	3	0	0	0	0	1	0	0	1	3
	0	0	0	0	0	1	0	0	2	0	0	0	0	0	1	0	1	2
	V 0	0	0	0	0	0	1	0 J	1	V 0	0	0	0	0	0	1	0 J	1
j	8	7	6	5	4	3	2	1	j	8	7	6	5	4	3	2	1

Supplementing the symbolic forms (8) and (10) of the Galois G and Fibonacci F matrices with the corresponding conjugate matrices G * and F * formed by the left-hand transposition of the base matrices,

G ( F ) ^^ G * ( F * ) =

E W 0 E^ е)Ц f >))

we arrive at the interconnection scheme (Fig. 9) of the subset of matrices, which we

denote { g } .

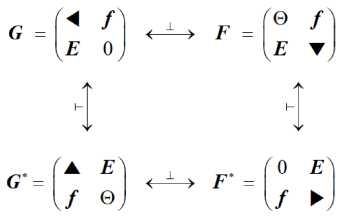
Fig.9. The diagram of the relationship between primary and adjoint Galois and Fibonacci matrices

The conjugate eighth-order Galois G * and Fibonacci F * matrices generated by transformations (12) of matrices

(11) have the form:

	Г 0	1	0	0	0	0	0	0 ^	8	Г 0	1	0	0	0	0	0	0 '	8
	1	0	1	0	0	0	0	0	7	0	0	1	0	0	0	0	0	7
	1	0	0	1	0	0	0	0	6	0	0	0	1	0	0	0	0	6
	0	0	0	0	1	0	0	0	5	0	0	0	0	1	0	0	0	5	(13)
G • =	0	0	0	0	0	1	0	0	4;     F • =	0	0	0	0	0	1	0	0	4.
	1	0	0	0	0	0	1	0	3	0	0	0	0	0	0	1	0	3
	0	0	0	0	0	0	0	1	2	0	0	0	0	0	0	0	1	2
	1 1	0	0	0	0	0	0	0 ,	1	1 1	0	1	0	0	1	1	0 )	1
	8	7	6	5	4	3	2	1		8	7	6	5	4	3	2	1

The complementary schemes of the LFSR generators are shown in Fig. 10.

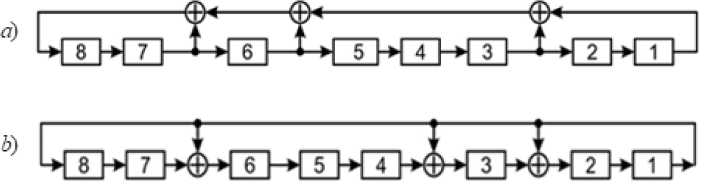
Fig.10. Block diagrams of coupled PRNG in configurations Galois a ) and Fibonacci b ) generated by PP f 8 = 101100101

• 3.    Efficient Algorithms for Calculating the States of Classical PRNG

• 4.    Generalized Hardware and Matrix PRNG According to the Galois and Fibonacci Schemes

The complexity of the algorithm for assessing the state of any of the four classical PRNG shown in Fig. 9 is, according to relation (1), O ( n ² ), i.e., increases in quadratic dependence on the order of the classical Galois matrices. Based on the structures of the CGM (first of all, due to their components — the unit matrices E of the ( n - 1) - order), it is possible to significantly reduce the computer time spent on assessing the state of the PRNG at the next ( k + 1) - th computation step.

For simplicity, let us introduce a notation system somewhat different from the one used earlier, assuming: V_k ={ v^_ _p v^ ₂,..., v , v ₀} — the PRN vector at the k - th generation step, in the curly brackets of which the binary components of the vector indicated; f = { а_и = 1, а_п__v ..., а , а₀ = 1 } — primitive polynomial generating CGM. The final relations that determine the vectors V for various CGMs are summarized in Table 3.

Table 3. State vectors of classical matrix PRNG

Matrices Galois	V k + 1		Matrices Fibonacci	V k + 1
G	- v n - 1 ' Л \ « n , « 0 ,    V k \ v n - 1      ’ vn - 1 n - 1 бит		F	V k \ V n - , , ® ( V k T® f n 1 ) n - 1 бит            1 бит
G	® ( V k T® f , t[ , V \ V, 1 бит           n - 1 бит		F *	V 0„«       V v 0 • fn \ « n , « 0, n - 1 бит

Table 2 arrows are located to the right of the column vectors f and V indicate the location of their senior elements, and f_n = { « 0 , «1,..., a _n } .

From the analysis of expressions for vectors V in Table 2, we conclude that the proposed algorithms for the formation of the PRN are much simpler than those stated above, and their computational complexity is O ( n ), i.e., linearly depends on the order of Galois matrices forming generators of binary pseudo-random sequences.

Definition 2. The subset of generalized PRNG of the maximum period will include generators built based on linear shift registers covered by multi-loop feedback. The feedback loop depends on an irreducible polynomial f (not necessarily primitive), playing a generating polynomial of the generator. And a forming element 0 > 10 , which is a primitive element of the field GF (2 ⁿ ), generated by the irreducible polynomial (IP) [15, 16].

The Galois matrix G ^{( n )} , through which the same PRN is generated programmatically and the sequence created by the generalized LFSR generator, will be called the generalized Galois matrix (GGM). The matrices G ^{( n )} synthesized according to a rule similar to the GGM G ^{( n )} , synthesis rule set out in Section 2. Namely

Algorithm for the synthesis of GGM : let f – an irreducible (not necessarily primitive) binary polynomial of degree n and 0 > 10 - the primitive element of the field GF (2 ⁿ ), generated by the polynomial. Place 0 in the lower right corner of the generated Galois matrix G ⁿ ^. All other digits of the bottom line G ⁿ ^, located to the left of the element 0 , are filled with zeros. Suppose the stage of formation of the next row its senior 1 goes beyond the left boundary of the matrix. In that case, the polynomial located in this row is reduced to the remainder modulo f . Thus, the row returns to the matrix, and the formation process G ^{( n )} continues further.

Let us consider examples of synthesis of a subset of primitive generalized Galois and Fibonacci matrices { G _g } g ( G g , F _g , G _g *, F _g *) and build on their basis the PRNG of the maximum period. Let us choose as an irreducible binary polynomial of the fourth degree f = 11111, which is not primitive, and a primitive forming element (FE) equal to 111. The matrices corresponding to the selected parameters have the form:

	"0110"		" 1   0   1   0 "
	0 0 11		1111
g =		;      F =		;
g	1110	g	1101
	_ 0   1   1   1 _		_ 0   1   0  0 _
				(14)
	"0010 "		" 1   1   1   0 "
	1011		0 111
G * =		;        F * =
g	1111	;                g	110 0
	_ 0   1   0   1 _		_ 0   1   1   0 _

The block diagram of the generalized primary four-bit Galois generator corresponding to the GGM G _g is shown in

Fig. 10. The vertically arranged registers of the generators, marked at the top by the symbol ® , implement the operation of bitwise multiplication. The registers marked with the symbol 0 — the operation of adding the contents of the register modulo 2. As memory elements, D - triggers are used as a rule.

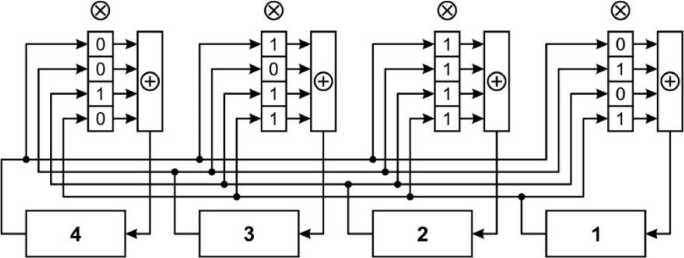
Fig.11. Block diagram of the basic generalized Galois generator

Replacing in Fig. 10 the contents of the cells of the vertical feedback registers by the elements of the matrix G * from the system (14), we obtain the circuit (Fig. 11) of the conjugated generalized PRNG in the Galois configuration. Block diagrams of PRNG shown in Fig. 10 and 15 just examples of LFSR generators with multi-loop feedback.

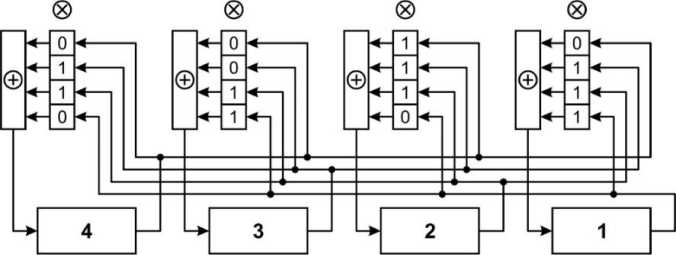
Fig.12. Block diagram of a conjugate generalized Galois generator

If in the graphs in Fig. 11 to replace the contents of the feedback register cells with matrix elements F and F * from the system (14), we come to the primary and conjugate generalized PRNG schemes in the Fibonacci configuration.

The fundamental difference between generalized Galois matrices { Q_g } and classical matrices { Q } is as follows. In CGM { Q } we can explicitly highlight the identity order matrix E , the zero column-vector, and the row-vector, containing the bits of the generator polynomial f . Generalized matrices { Q_g } do not have such features. From it follows that for the set matrices { Q _g } there are no compact forms similar to the forms (8) of matrices { Q } .

A diagram of the relationship between classical matrices { Q } and generalized Galois matrices { Q _g } conveniently presented in the form of a Table 4.

Table 4. Interrelation of Galois and Fibonacci matrices

	G	F	G *	F ’
G	–	1	T	1 Т
F	1	–	1 Т	T
G *	T	1 Т	–	1
F *	1 Т	T	1	–

The variety of Galois generators of pseudo-random sequences can significantly expand by introducing a similarity transformation for classical and generalized Galois matrices that generate the PRNG. The similarity transformation, being a linear transformation, preserves the original generalized Galois matrices [13, 14]. If { Q _g } a family of primitive matrices, then after the similarity transformation, the matrices remain primitive. We will call primitive such square matrices with elements a i , j e Z _p , the sequence of degrees (starting from the zero degrees) in the field GF ( p ) forms a series of maximum lengths.

• 5.    Generalized Matrix Galois PRNG over a Field off odd Characteristics

The developed synthesis algorithms for binary matrix Galois PRNG are easily generalized for constructing PRNG over a field of odd characteristics p . The Galois matrices corresponding to such generators are denoted by G (n)  . The matrix G(n) synthesis algorithm coincides with the above algorithm for the synthesis of binary GGMs G (n). In this case, in the text of the algorithm, it is enough to perform only such simple replacements: GF(2n) ^ GF(pn) and (n)              (n)

^G f , e ^ G f , e , p ^.

Let us look at an example. Let n = 4 , p = 3 , f = 12121 and e = 221. The parameters include an irreducible polynomial f , the exponent of 10, and e- a primitive element of the field GF (3 ⁴ ), generated by the IP f . The selected parameters correspond to the system of generalized primitive Galois and Fibonacci matrices over GF (3)

"0 1 2 2" "1 0 1 2" G = 1 2 2 2 2 1 1 0 ,    F = 2 2 1 2 2 2 2 1 , _0 2 2 1_ _0 2 1 0_ (15) "0 1 2 0" "1 2 2 0" G * = 2 2 2 2 1 2 2 ,     F * = 1 1 2 2 2 2 1 , _2 1 0 1J _2 2 1 0_ in which letter indices are omitted for simplicity.

Using the matrix G of system (15) and the generator circuit shown in Fig. 10, we will compose a generalized structural logic diagram (Fig. 12) of a ternary four-bit register PRNG in the Galois configuration. The numbers 3 located in the vicinity of the operators of bitwise multiplication and addition mean that the calculations carried out modulo 3. It also assumed that the register D - triggers transfer ternary numbers from the input to the output.

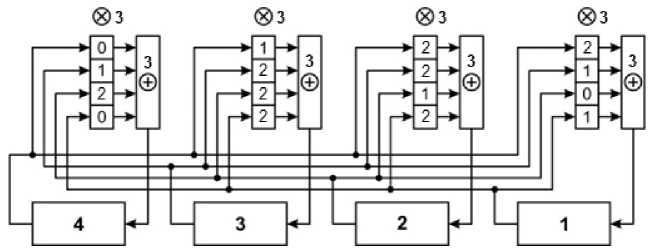
Fig.13. Block diagram ofthe generalized Galois generator over IP f = 12121

Table 5. A sequence of ternary vectors generated by the registered (Fig. 16) and matrix G(n’  ( e = 221 ) generators of the PRN over the IP f =12121

1		0	0	0	1		0	0	1	0		0	1	0	0		1	0	0	0		1	2	1	2
2		0	2	2	1		2	2	1	0		1	2	2	1		0	1	2	2		1	2	2	0
3		0	1	2	0		1	2	0	0		0	2	1	2		2	1	2	0		0	0	2	1
4		2	0	1	1		2	2	0	1		1	1	0	1		2	2	2	2		1	0	1	1
5		2	0	1	2		2	2	1	1		1	2	0	1		0	2	2	2		2	2	2	0
6		2	2	0	0		1	1	2	1		2	1	2	2		0	0	1	1		0	1	1	0
7		2	0	2	0		2	0	2	1		2	0	0	1		2	1	0	1		0	1	0	1
8		1	0	0	1		1	2	2	2		0	1	0	2		1	0	2	0		1	1	1	2
																						0	0	0	2

An alternative register generator shown in Fig. 12 is a matrix PRNG, which by expression (1), generates the same sequence of pseudo-random ternary codes as a registered generator (see Table 5).

Table 5 contains only the first half of the sequence of the maximum period, consisting (for the selected values of the generator parameters) of 80 ternary four-digit codes. The second half of the sequence, starting with code 0002, is formed from codes of the first half due to their bitwise multiplication by 2 modulo 3.

• 6.    Cryptographic Resistance of Generalized Galois Matrix Generators of PRN to Berlekamp-Messi Attack

• 7.    Result and Future Scope

Classical primitive Galois matrices of order n and generalized matrices can serve as generators of PRNs of length L = 2 n — 1. These sequences satisfy all three postulates of Golomb [17]. For this reason, one might get the impression that generalized Galois PRNG do not introduce any new properties in the sequences formed by classical generators. Since the latter is more superficial in hardware and software implementation, it is possible that the use of generalized generators, for example, for cryptographic applications, can turn out to be impractical. However, it is not so. As established in [8], PRNG built based on generalized Galois matrices are free from the BM attack. The noted feature of generalized generators appears for the following reason. For classical generators with a single-loop feedback circuit, the BM tester successfully solves the problem of determining only one unknown - the generating PP f . When generalized generators are broken, in addition to f the primitive forming element 9 of the Galois matrix is also unknown. However, the classical BM algorithm is not designed to calculate two unknown parameters and therefore becomes inconsistent when organizing an attack on generalized generators. Besides, in any case (whether the conditions of applicability of the BM algorithm met or not), the processor that implements the BM algorithm as a solution always outputs this or the value of the PP f , while the generalized Galois PRNG can be built based on a polynomial, not necessarily primitive.

Let us turn to a variant of the eighth order Galois matrix generator, taking as the generating PP f 8 = 100011101 . Whichever primitive forming element is chosen, the solutions of the BM tester, summarized in Table 5, will always be one of the 16 primitive polynomials of the eighth degree.

Table 5. BM tester solutions on a set of forming elements of the field GF (2 8 ) generated by PP f = 100011101

PP	Forming elements
	1	2	3	4	5	6	7	8
100011101	002	010	020	035	114	137	205	235
100101011	006	015	024	121	207	302	321	332
101110001	011	026	101	107	203	216	314	330
100101101	016	033	124	130	220	227	300	336
101101001	022	023	030	031	134	135	200	201
101100101	036	103	111	132	214	224	236	310
101100011	037	102	110	133	215	225	237	311
111000011	042	160	167	173	244	253	261	341
110101001	043	161	166	172	245	252	260	340
110000111	050	064	071	074	077	171	273	345
110001101	052	060	143	151	242	274	367	370
111110101	053	061	142	150	243	275	366	371
111100111	062	155	257	343	350	352	356	376
101011111	112	122	211	232	306	312	323	324
101001101	113	123	210	233	307	313	322	325
111001111	157	176	262	267	354	360	363	372

According to Table 5, eight FEs, represented in the top row of the Table by three-digit octal numbers, are such that each leads to the correct solution produced by the BM tester. We will call such FE "weak keys" of a stream cipher, the encryption gamut formed by the analyzed PRNG. The fact that weak keys lead to the correct solution of the BM tester does not mean that the PRN generated by the generalized generator will coincide with the sequence formed by the classical generator with single-loop feedback. These sequences will overlap if the element highlighted in bold in the Table selected as a forming element of the matrix. This FE value degraded because it converts the generalized PRNG to the classic single-loop LFSR generator.

Eliminating weak keys of generic PRNG is quite simple. For this purpose, it is sufficient to choose a non-primitive polynomial f as the generator. In this case, the BM tester will produce a deliberately erroneous decision.

The main results of this work are:

• 1.    Various options have been developed for constructing binary PRNG based on the so-called generalized Galois and Fibonacci matrices. The identical binary sequences can programmatically calculate as the sequences formed by the corresponding hardware LFSR generators. The transition from classical to the generalized matrix (or hardware) PRNG accompanied by expanding the variety of generators leads to a significant increase in their cryptographic strength. This effect is achieved both due to the rise number of elements forming the generating matrices. Az generalized matrices synthesized not only based on PP (the only possible polynomials used in the synthesis of classical generators) but also based on polynomials, not necessarily primitive.

• 2.    It has shown that generators of generalized PRN matrices are not subject to BM attacks. The noted property is a consequence of such a feature of the BM algorithm. In violation of the classical PRNG, the BM algorithm solves computing the only unknown: the primitive polynomial f that the generator generates. In generalized PRNG, it becomes necessary to determine two unknown parameters: both the irreducible polynomial f and the generating element θ with the help of the generalized matrix. This problem turns out to be insoluble for the BM algorithm.

• 3.    The research results are generalized for solving the synthesis of PRNG over the Galois field of odd characteristics.

• 4.    The developed synthesis algorithms generalized Galois and Fibonacci matrices can construct cryptographically robust systems for stream encryption of information and other cryptographic applications.