Generation of An Efficient Digital Watermark Key Based on Honey Comb Polynomial Interpolation Approach

Published Online March 2013 in MECS

A watermark is a unique or special image that is embedded on a paper or document that consist text or images. The watermark is designed in a way that it appears only when it is viewed by transmitted light or holding it in a particular angle [12, 24, 25]. Watermarks are used to identify the owner of the image/content and to prevent counterfeiting them. But, this was not possible in digital content. The vast growth of Internet has allowed users to copy the digital content and distribute them without control of ownership. Copy protection system is one of the widely used applications of digital watermarking [9, 23]. It can be used either to prevent unauthorized copies of digital media or tracking the source of any data. Digital watermarking techniques provide high security to digital content by allowing only authorized person(s) to modify or detect the watermark [10]. Some recent watermark techniques [14, 15, 16, 17, 18, 19, 20] prevent others from modifying or detecting the embedded watermark in a digital content. Watermarks that are embedded on a digital content should be imperceptible both statistically and perceptually. Once the watermark is embedded in a digital content, it is not possible to retrieve the original content by separating the watermark from the content. The quality of an image should not get affected when a watermarking is embedded to it. i.e, when a watermark is embedded in an image, it should not be visible to the naked eye. Each application might have data with different sizes to be embedded as watermark. The perceptual impact and robustness will be directly affected because of various sizes of data. Possibility is always there for a user to know the exact algorithm to detect and render to inactivate a watermark. Therefore, selecting a unique key for watermarking is the only way to secure it. Now, it is impossible for the unauthorized user to know the exact key even if he/she knows the exact algorithm. This increases the strength or reliability of the watermark.

Visible watermarks are similar the paper watermarks, as the watermarks will be visible to the naked eye. Invisible watermarks are imperceptible and cannot be viewed through naked eye. Numbers of techniques are used to implement invisible watermarking. An invisible watermark can be either robust or fragile. The use of a fragile watermark is important when one wants to verify if the protected media was tampered with or not. Robust watermarking is a technique in which modification to the watermarked content will not affect the watermark [12, 13, 21, 22]. In order to further performance improvements in digital image watermarking algorithms the proposed method used two stages and MPSPVD and HCPI. The reason of applying two stages is to get good quality watermarked image for effective watermarking.

The rest of the paper is organized as follows: Section 2 focuses brief introduction about related works. In section 3, describes the method for embedding and extraction watermark for proposed watermarking scheme. Section 4 shows experimental results after implementation and testing the scheme. The conclusion as well as the future work will be discussed in the final section.

• II.    R elated works

• A.    Interpolation Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables (also known as indeterminate) and constants, using the operations addition, subtraction, multiplication, and non-negative integer exponents. The exponents are only being 0, 1, 2, 3… etc. It cannot have an infinite number of terms. Polynomials appear in a wide variety of areas of mathematics and science. For example, they are used to form polynomial equations which encode a wide range of problems from elementary word problems to complicated problems in the sciences. The derivative of the n degree polynomial is given by Equation (1)

а„ХИ + On-^""1 + *" + °2x2 + Qlx + Q0(1)

• B.    Lagrange Interpolation Polynomial

Lagrange Interpolation formula is one of the most commonly used interpolation functions and its computation charge is inferior to the majority interpolation functions. An interpolation is defined as a function which contains independent variable and a number of parameters. When constructing interpolating polynomials, there is a tradeoff between having a better fit and having a smooth well-behaved fitting function. The more data points that are used in the interpolation, the higher the degree of the resulting polynomial, and therefore the greater oscillation it will exhibit between the data points. Therefore, a high-degree interpolation may be a poor predictor of the function between points, although the accuracy at the data points will be ‘perfect’.

The Lagrange Interpolating Polynomial [3] can be defined as P(x), which is given in the Equation (2).

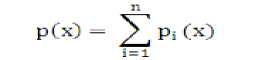
P5C^) У5ПЕ Xk»! ^„^          (2

Written explicitly,

, . _   (x- x2)(x-x3)„. (x-xn) (x- xJCx-x^-Cx-x,) , px- (Xl -X2)(Xj -X3)(X! -xj^ (x2 -XjJtXj -x3)(x2-x„)y‘

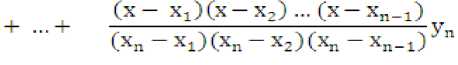
L¹^______ . l§ stand for the parameters in Lagrange

Interpolation formula that can be computed by n+1 given points, as showed in Equation (3).

• C.    Mathematical morphology

Mathematical morphology is a well-founded non-linear theory of image processing. Its geometry-oriented nature provides an efficient framework for analyzing object shape characteristics such as size and connectivity, which are not easily accessed by linear approaches. Morphological operations take geometrical shape of the image objects into consideration for analysis.

Mathematical morphology is theoretically founded on set theory. It contributes a wide range of operators to image processing, based on a few simple mathematical concepts. The operators are particularly useful for the analysis of binary images, boundary detection, noise removal, image enhancement and image segmentation. An image can be represented by a set of pixels. A morphological operation uses two images: the original data image to be analyzed and a structuring element (also called kernel) which is also a set of pixels constituting a specific shape such as a line, a disk or a square. A structuring element is characterized by a well-defined shape (such as line, segment or ball), size and origin. Its shape can be regarded as a parameter to a morphological operation.

The basic operation of a morphology-based approach is translation of a structuring element over the image and the erosion and/or dilation of the image content based on the shape of the structuring element. So far only few researchers used morphological principles in developing schemes for Digital Watermarking (DW). That is the reason the present study introduced morphological schemes for HCPI method of DW.

• D.    Fundamental Definitions

The fundamental mathematical morphology operations dilation and erosion based on Minkowski algebra are defined by the following Equations (4) and (5).

Dilation- D ( A , B ) = A Ф B = J ( A + в       (4)

β ∈ B

Erosion E ( A , B ) = A 0 ( - B ) = J ( A - в )       (5)

β∈B where - B = {в1 в£ B} these two operations are illustrated in Figure 1. While either set A or B can be thought of as an image, A is usually considered as the image and B is called a structuring element.

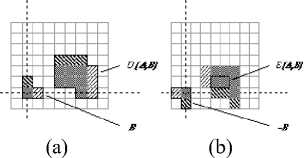
Figure 1. A binary image containing two object sets A and B . (a) Dilation D( A , B ) (b) Erosion E( A , B )

Dilation, in general, causes objects to dilate or grow in size; erosion causes objects to shrink. The amount and the way that they grow or shrink depend upon the choice of the structuring element. Dilating or eroding without specifying the structural element makes no more sense than trying to low pass filter an image without specifying the filter. Dilation and Erosion have the Commutative Non-Commutative Associative Translation Invariance and Duality properties.

• E.    Boundary extraction

Let R be a subset of pixels in an image. Then one can call R is a region of the image if R is a connected set. The boundary (also called border or contour) of a region R is the set of pixels in the region that have one or more neighbors that are not in R. If R happens to be an entire image (which is a rectangular set of pixels), then its boundary is defined as the set of pixels in the first and last rows and columns of the image. This extra definition is required because an image has no neighbors beyond its border. Normally, a region refers to a subset of an image, and any pixels in the boundary of the region that happen to coincide with the border of the image are included implicitly as part of the region boundary.

A boundary point of an object in a binary image is a point whose 4-neighborhood (or 8-neighborhood depending on the boundary classification) intersects the objects and its complement. The classification of boundaries for binary images is done by their connectivity and whether they lie within the object or its complement. Thinning methods are used for boundary transformations of the binary image. But the homotopy of the original image could not be preserved.

• F.    Sorted Pixel Value Difference(SPVD) Method

The basic PVD scheme [4E] is meant for watermarking images. This scheme offers high imperceptibility to the watermarked image by selecting two consecutive pixels as the object of embedding. The payload is determined by the difference value between the pixels as given below.

The basic PVD method, determines whether the two consecutive pixels belong to an edge or smooth area by checking out the difference value between two consecutive pixels. If the difference value is large, i.e. the two pixels are located in an edge area; more secret data can be hidden here. On the contrary, if the difference value is small, i.e. the two pixels are located in a smooth area; less secret data can be embedded. Therefore, this scheme produces watermarked images that are more similar to the original images than those produced by LSB substitution schemes, which directly embed secret data into the cover image without considering the differences between adjacent pixels.

Given a cover image I of size M×N, I i is a sub block of I that has two consecutive pixels broken down by partitioning I in raster scan order such that I={ I i /i=1,2,……..(M×N)/2}. By definition each I i has two elements E (r,L) and E (r,R). The pixel values of E (r,L) and E (r,R) are V (r,x) and V (r,y) respectively. The difference value d i of V (r,x) and V (r,y) can be derived by Equation (6).

d i = |V (r,x) -V (r,y) | (6)

The range Table 1 which consists of n contiguous sub ranges T j ; T= {T j | j=1, 2,..n}, provides major information about the hiding capacity of I i . Each sub range T j has its lower and upper bound values, say l j and u j , so that it will have T j € [l j , u j ]. The width w j of each T j is selected to be a power of 2, and can be computed by w j =u j -l j +1.Each sub block I i relates to its sub range T j from the range Table 1 such that T j =min(d i ,w j ) and d i €[l j ,u j ]. This way, the hiding capacity of two consecutive pixels can be obtained by Equation (7).

b i = log (w j ) (7)

Here, b i is the number of bits that can be hidden in I i . The range Table 1 of PVD method clearly indicates the number of bits of watermark to be selected. The detailed mechanism of PVD can be found in [26].

Table 1 Range table showing hiding capacity

Range	l j	u j	w j	b i =log(w j )
T1=[0,7]	0	7	8	3
T2=[8,15]	8	15	8	3
T3=[16,31]	16	31	16	4
T4=[32,63]	32	63	32	5
T5=[64,127]	64	127	64	6
T6=[128,255]	128	255	128	7

• III.    P roposed HCPI-MBSPVD ALGORITHM FOR WATERMARKING

• A.    Watermark embedding technique

  Original Image

  
  
  

  Identify HCS pixels

  
  

  Polynomial Interpolation

  
  
  

Step2: Construction of HCP table

Select the n-pixels from non-overlapped HCS and store them in HCP Table as given in Figure 5.

1       2        3       4                                                    N-1      N

Generating

Watermark Key

129

55

67

74

104

54

Figure 5. HCP table

Watermark Key Insertion

Watermarked Image

Figure 2. Embedding technique of the proposed HCPI-MBSPVD

The watermarking algorithm which is used to embed the watermark in the host image is summarized in Figure 2. The proposed HCPI-MBSPVD consists of two stages. In the first stage DWK is generated. In the second stage DWK is embedded in the image using MBSPVD method. The first stage consists of four steps as explained below.

Stage 1:Step1: Identification of HCS

To identify n random pixels, where n is the size of the grey level logo, from the original image, HCS is used in the present paper. The importance of HCS representation is that it possesses special computational features that are pertinent to the vision process [1E, 2E]. In the present paper HCS’s are constructed from the 24×23 size, and it consists of 7 hexagon regions. Figure 3 shows a collection of seven hexagon regions forms a HCS. The centre sub pixels of interior hexagonal structure or Honey Comb Pixels (HCP) are selected for key generation and they are marked as P i = (i= 0, 1, 2,…6) as shown in Figure 3. Figure 4 illustrates internal Hexagonal Structure of HCP’s. From each internal structure centre pixel is chosen as HCP.

Step3: Construction of Grey Level Watermark Table (GWT)

Arrange the grey level watermark pixels in a one dimensional array [1…N] of pixel values with row major order. The Figure 6 gives the GWT of n-pixels, arranged in a similar way to HCP table.

1    2     3    4                                    N-1 N

45

67

98

16

24

75

Figure 6. GWT of N pixels

Step4: Generation of Digital Watermark Key Table (DWKT)

The proposed method derived a polynomial equation for construction of DWKT using mod 255 operator as shown in Equation (8).

К!х) = ■ o^r'a,, pi¹'-' I—Н а₂х² + аре + a₀ ) (mod 255)    (8)

This equation generates a key for each x value ranging from 1 to 255. In the Equation (8),^ s &n-v ■•• «о is the pixel values of watermark represented in GWT. DWKT is generated by matching the obtained values of function K(x) with HCP table. If there exists an x, in K(x) = HCP j then store x to the j^th entry of DWKT as shown in Figure 7.

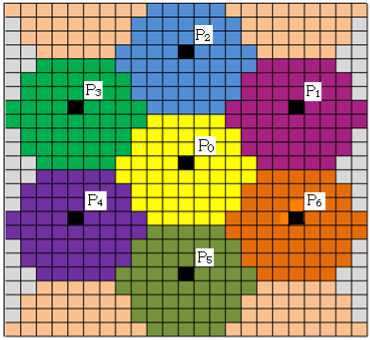
Figure 3. Representation of Honey Comb structure

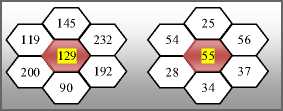
Figure 4. Honey comb structure with HCP’s

The DWKT consists of n-pixels, arranged in a similar way to HCP table. The advantage of the DWKT is it acts as an encrypted watermark. The novelty of the proposed method is the original watermark can be generated by using LPI with HCP and DWKT.

Stage 2:

In the second stage the WKT is placed in the original image by using MBSPVD. In MBSPVD, on the original image the morphological border locations are identified. Then watermark key is embedded in the sorted pixel locations of morphological border pixels, other than HCP’s, of the original image by using SPVD. This approach overcomes the weak robustness problem of embedding the watermark.

Step1: Consider a structuring elements E r of different directions of a neighborhood. Borders G r (D)are detected by morphological gradient border detection method by using E r on original image.

6,(0) = (FSB) - (FOB) (9)

1     2      3     4                                       63       64

Q 1

5

Q

Q 4

Q 63

Q 64

Figure7. Function values of DWKT where means dilation, means erosion, F is the original image and F is the original image.

Step2: On detected border G r (D) of step 1, synthetic weighted method is used, to overcome the falling boundary problem and distortions at borders, as given in Equation (12).

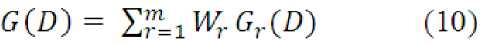
Where G(D) is the final detected border of original image, m is the number of structuring elements and w r is the weight of detected border information.

Step3: The border pixel, other than HCP pixels are identified in the original image.

Step4: The fourth step, groups only those pixel coordinates on the original image selected by step 3, based on their pixel values in ascending order. If two or more pixels are having same values then they will be sorted by row wise positions.

Step5: The watermark key is inserted on the group of pixels in the sorted order by using SPVD method. SPVD is similar to PVD method. By inserting watermark key, the pixel value may be changed; and the sorted order may also be changed. The quality of the watermark key is affected if the sorted order is changed after inserting the watermark key bits by pixel value differencing method. To overcome this, in the proposed SPVD method watermark is inserted in the group of two pixels, if its values after inserting watermark are less than the next group of values.

• B.    Watermark extraction technique

The entire extraction process of the proposed HCPI-MBSPVD method is as shown in Figure 8.

Step 5: Watermark pixels are generated from the HCP and DWK tables .

• IV.    RESULTS AND DISCUSSION

The proposed HCPI-MBSPVD method is experimented on all 5 images “Monalisa”, “Cameraman”, “Boy”, “House” and “Joker” of size 256×256 of Figure 9. The gray watermark considered for the experiments is logo ‘Rose’ of size 32×32 as shown in Figure 10. Figure 11 represents the boundary images based on proposed morphological boundary algorithm given in stage2. Figure 12 represents the watermarked images using HCPI-MBSPVD method. The watermark key bits are inserted in the boundary pixel locations, other than HCP’s of the original image. Table 2 shows the PSNR and NCC values for all the 5 images. From the Table 2 it is clearly evident that all the images shows high PSNR and NCC values which indicates high robustness and high quality of image after watermark insertion.

(a)

(d)            (e)

Figure 9. Original images (a) Monalisa (b) Cameraman (c) Baby (d) House (e) Joker

Watermarked Image

Extract watermark

Original Image

Figure 8. Extraction technique of the proposed HCPI-MBSPVD method

Steps of watermark extraction process are as follows

Step 1: From the watermarked image, detected the border G r (D) by using Equations (9) and (10) . Eliminate HCP from G r (D.

Step 2: Perform SPVD to get watermark key table from G r (D.

Step 3: Identify the HCP table from HCS.

Step 4: Using HCP table and DWKT values extract watermark by implementing Lagrange Polynomial Interpolation (LPI).

(a)

Figure 10. Watermark image (a) Logo “Rose”

(a)             (b)              (c)

(d)             (e)

Figure 11. Boundary images (a) Monalisa b) Cameraman (c)

Baby    (d) House (e) Joker

(a)                            (b)                        (c)

(d)            (e)

Figure 12. Watermarked images (a) Monalisa (b) Cameraman (c)

Baby        (d) House (e) Joker

Table 2 Quality measures of proposed HCPI-MBSPVD

Test images	proposed HCPI-MBSPVD
	PSNR(dB)	NCC
Monalisa	55.38	1
Cameraman	56.38	1
Boy	56.35	0.98
House	55.28	0.98
Joker	56.29	0.99

• A.    Proposed HCPI-MBSPVD watermarked images under various under attacks

The proposed method is tested with various attacks. Watermarking techniques are usually tested against various robustness criteria. The proposed watermarking technique is tested by using the different geometric attacks and different watermarks are embedded in the standard test images “Baboon”, “Boat”, “MRI brain”, “Flower”, “Lena” and “Peppers”. The watermarked images are cropped with percentage of 10%, 15%, 25%, Rotated with an angle of 20, 40, 60, adding Gaussian and salt and Pepper noise of 10%, 15%, 20%, Median filtered with a window size of 3×3, 5×5, 7×7, Gaussian Blurring with 5%,10%,15%, Motion blurring with 5%,10%,15%, JPEG compression quality factor of 90%, 80%, 70% and Sharpening of 5%,10%,15% of image. The PSNR and NCC values, for the grey level logo ‘Rose’ of Table 3 and 4 clearly indicate the robustness and quality of the image is not degraded for all attacks by the proposed HCPI-MBSPVD method.

The resultant watermarked Monalisa with attacks of various geometric transformations such as Median filter, Cropping, Rotation, Salt and pepper noise, Gaussian noise, JPEG compression, Gaussian blurring, Motion blurring and Sharpening which are presented in Figure 13. The proposed watermarking technique preserves robustness to all geometrical transformations. Figure 14 shows gray watermark logo images from the different attacked watermarked images. The extraction algorithm extracted more than 70% of the watermark.

Table 3 Quality results of the experiments on HCPI-MBSPVD method with various attacks on the watermarked images with logo ‘Rose’

Type of Attack	Babo on	Boat	MRI brain	Flower	Lena	Pepper
	PSNR(dB)
Median filter (3×3)	43.34	43.48	46.32	46.27	46.67	46.44
Median filter (5×5)	42.23	43.76	44.74	44.48	44.38	44.23

Median filter (7×7)	39.47	40.47	42.27	42.38	42.67	42.43
Cropping 5%	44.36	44.48	44.84	44.28	44.39	44.63
Cropping 15%	43.24	43.68	43.28	43.64	43.12	43.76
Cropping 25%	41.09	40.37	41.74	40.27	41.49	40.24
Rotate 20	44.46	44.48	44.27	44.42	44.62	44.73
Rotate 50	42.87	43.29	42.34	43.73	42.21	43.13
Rotate 60	40.98	40.17	40.84	40.83	40.64	40.67
Salt and Pepper Noise 10%	44.39	44.39	44.27	44.92	44.49	44.94
Salt and Pepper Noise 15%	43.46	43.69	43.16	43.11	43.37	43.32
Salt and Pepper Noise 20%	41.37	41.46	41.48	41.09	41.32	41.84
Gaussian noise 10%	44.34	44.67	44.93	44.34	44.69	44.84
Gaussian noise 15%	43.16	42.67	43.37	42.26	43.43	42.24
Gaussian noise 20%	41.49	40.28	41.28	40.72	41.72	40.84
JPEG Compression 90%	44.37	46.49	44.74	46.14	44.44	46.84
JPEG Compression 80%	43.84	43.49	43.27	43.29	43.84	43.434
JPEG Compression 70%	41.62	41.49	41.48	41.71	41.44	41.494
Gaussian Blur 5%	46.39	46.38	46.26	46.44	46.86	46.13
Gaussian Blur 10%	43.28	44.39	43.38	44.44	43.43	44.43
Gaussian Blur 15%	41.38	41.98	41.24	41.87	41.74	41.27
Motion blurring 5%	46.36	46.48	46.94	46.48	46.34	46.44
Motion blurring 10%	43.47	43.01	43.21	43.01	43.84	43.07
Motion blurring 15%	40.67	40.38	40.38	40.38	40.43	40.44
Sharpening 5%	44.98	44.38	44.64	44.38	44.42	44.31
Sharpening 10%	43.67	43.37	43.33	43.37	43.87	43.47
Sharpening15%	41.12	41.27	41.38	41.27	41.39	41.21

Table 4 Correction results of the experiments on HCPI-MBSPVD method with various attacks on the watermarked images with logo ‘Rose’

Type of Attack	Babo on	Boat	MRI brain	Flower	Lena	Pepper
	NCC
Median filter (3×3)	0.81	0.88	0.86	0.87	0.84	0.86
Median filter (5×5)	0.79	0.84	0.78	0.80	0.81	0.81
Median filter (7×7)	0.76	0.74	0.72	0.76	0.76	0.75
Cropping 5%	0.88	0.87	0.83	0.82	0.85	0.87
Cropping 15%	0.81	0.82	0.78	0.78	0.80	0.82
Cropping 25%	0.75	0.73	0.68	0.68	0.75	0.74
Rotate 20	0.83	0.84	0.82	0.84	0.82	0.82
Rotate 40	0.74	0.73	0.73	0.76	0.73	0.75
Rotate 60	0.68	0.70	0.71	0.71	0.68	0.68
Salt and Pepper Noise 10%	0.88	0.84	0.88	0.87	0.87	0.86

Salt and Pepper Noise 15%	0.78	0.78	0.78	0.78	0.78	0.78
Salt and Pepper Noise 20%	0.71	0.72	0.72	0.71	0.72	0.72
Gaussian noise 10%	0.87	0.86	0.84	0.84	0.87	0.86
Gaussian noise 15%	0.75	0.74	0.76	0.76	0.74	0.74
Gaussian noise 20%	0.70	0.71	0.71	0.70	0.71	0.71
JPEG Compression 90%	0.88	0.87	0.84	0.87	0.88	0.87
JPEG Compression 80%	0.78	0.76	0.76	0.74	0.76	0.78
JPEG Compression 70%	0.72	0.70	0.70	0.68	0.74	0.73
Gaussian Blur 5%	0.86	0.84	0.84	0.84	0.83	0.85
Gaussian Blur 10%	0.78	0.77	0.77	0.83	0.78	0.77
Gaussian Blur 15%	0.74	0.70	0.70	0.79	0.74	0.69
Motion blurring 5%	0.82	0.81	0.79	0.79	0.80	0.81
Motion blurring 10%	0.78	0.74	0.77	0.78	0.78	0.78
Motion blurring 15%	0.72	0.68	0.73	0.72	0.71	0.73
Sharpening 5%	0.88	0.80	0.84	0.88	0.86	0.86
Sharpening 10%	0.78	0.73	0.78	0.76	0.78	0.76
Sharpening15%	0.71	0.67	0.71	0.71	0.72	0.70

Figure13. Attack watermarked images (a) Median filter (3×3, 5×5,7×7) (b) Cropping (10%, 15%, 25%) (c) Rotation (20, 50, 60) (d) Salt and pepper noise (10%, 15%, 20%) (e) Gaussian noise (10%, 15%, 20%) (f) JPEG compression (90%, 80%,70%) (g) Gaussian blurring (5%, 10%, 15%) (h) Motion blurring (5%, 10%, 15%), (i) Sharpening (5%, 10%, 15%)

Figure14. Retrieved gray logo images (a) Median filter (3×3, 5×5,7×7) (b) Cropping (10%, 15%, 25%) (c) Rotation (20, 50, 60) (d) Salt and pepper noise (10%, 15%, 20%) (e) Gaussian noise (10%, 15%, 20%) (f) JPEG compression (90%, 80%,70%) (g) Gaussian blurring (5%, 10%, 15%) (h) Motion blurring (5%, 10%, 15%), (i) Sharpening (5%, 10%, 15%)

• B.    Comparison of the proposed HCPI-MBSPVD with the existing methods

Table 5 compares the PSNR values after inserting the watermark key without attacks by the proposed HCPI-MBSPVD method with various other methods [5, 6, 7, 8]. Table 5 clearly indicates the HCPI-MBSPVD outperforms the other existing methods. A graph is also plotted in Figure 15 which indicates the comparison of the proposed HCPI-MBSPVD method with various other methods without attacks.

Table 5 Comparison of the proposed HCPI-MBSPVD method with various other methods

Test Images	T.K. ariet.al	Dong-Gyu Yeo et.al method	Baisa L. Gunjal et.al method	S.Maruthu perumal et.al method	Proposed HCPI-MBSPVD
Monalisa	42.89	36.34	40.98	45.47	55.38
Cameraman	42.56	36.12	42.52	44.56	56.38
Boy	42.87	36.58	41.36	45.06	56.35
House	42.64	37.93	42.47	47.28	55.28
Joker	42.78	36.37	41.36	46.23	56.29

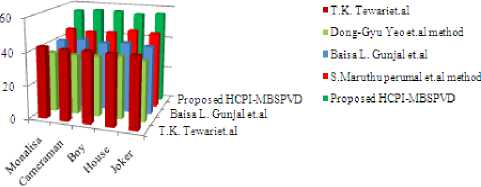
Figure15. Comparison graph of the proposed HCPI-MBSPVD with various other methods

• V. C onclusions

In this paper, we have proposed a novel image watermarking technique called HCPI-MBSPVD which allows a trusted authority to recover the ownership from any reasonably attacks. In order to do so, we embed a DWK using HCP in a redundant way, exploiting a suitable polynomial interpolation. The polynomial representation makes the digital watermark in to an encrypted water mark. The polynomial interpolation given a high secured DWK, which is difficult to break.

The decryption process requires Lagrange interpolation method, HCP and DWK tables. This gives the ability of this method to efficiently code whole watermark without error and with high speed. This proposed system given good results in formation of DWK. The importance of HCS representation is that it possesses special computational features that are pertinent to the vision process. The HCS has features of higher degree of circular symmetry, uniform connectivity, greater angular resolution, and which leads to reduce storage and computation in image processing operations. The proposed HCPI, HCP, LPI and morphological border detection techniques are almost always be obtained even in the presence of image degradation operators and independently of the image characteristics without any error. Furthermore, the proposed method shows high performance even in critical situations like in the presence of various attacks. The experimental results indicate the efficacy of the proposed method even in the presence of noise. The experimental results on various images with various attacks show that the proposed technique HCPI-MBSPVD provides good image quality and robustness when compared to other methods. The proposed HCPI-MBSPVD method allow easier processing of image data and require less computational power, at the same time by providing higher robustness, high payload, imperceptibility, it produces high quality watermarked image and resistant to attacks. Finally we stress that our HCS and morphological approach is not constrained by the kind of watermarking technique adopted in the present paper. Indeed, it can be combined with techniques different from that proposed in this paper in such a way to respond to other application requirements of digital watermarking. This aspect represents one of the envisaged future works. The watermark extraction also does not require the original image so the application is more practical in real time application for ownership verification.