Генератор хаотического сигнала с постоянной амплитудой

Обычный метод генерации хаотического сигнала, с постоянной амплитудой (фазового хаоса) заключается в преобразовании амплитудного хаоса. На вход ГУНа (генератора, управляемого напряжением) подается сигнал с хаотической амплитудой, на. выходе ГУНа будем иметь хаотические колебания с постоянной амплитудой. В этом случае мы должны иметь источник колебаний с хаотической амплитудой.

Другое решение заключается в использовании цепи ФАН (фазовой автоподстройки) с нелинейным элементом [1].

Третье решение — цифровые методы генерации [2]. Их недостаток — низкая частота, генерируемого сигнала.

В данной работе предложена, схема, генерации хаотического сигнала, с постоянной амплитудой, работа, которой основана, на. нелинейной зависимости длительности задержки выходного сигнала, зарядового усилителя считывания от дифференциального сигнала, на. входах. Схема, генератора, (рис. 1а) состоит из усилителя считывания, логического элемента. ИЛИ, двух кольцевых генераторов. Может использоваться один входной кольцевой генератор, в котором будут использоваться два. выхода, сдвинутые относительно друг друга, по фазе (рис. 16). Последняя схема была промоделирована на транзисторном уровне.

Рис. 1

Упомянутый выше усилитель (рис. 2а.) работает в два. этапа. На исходном состоянии на. линии СИ высокий уровень напряжения, на. линии предзаряда. низкий уровень напряжения, и на. линии разрешения УС — высокий уровень напряжения. Проходные транзисторы М3 и М4 закрыты. Схема, предзаряда. высоким уровнем включена. М5 и Мб открыты. Ml и М2 закрыты и на узлы динамического RS-триггера подан низкий уровень напряжения.

На первом этапе на линию СИ подается низкий уровень, на линию предзаряда высокий, на линию разрешения УС высокий. Схема предзаряда отключена. Проходные транзисторы М3 и М4 открыты. Начинается процесс чтения, и напряжение на битовой линии падает. Предположим, что считывают на входе вх1 напряжение выше напряжения на входе вх2, ток на al — г _а 1 , ток на а2 — г _а 2 , где |г_а1| < |г_а2|. Транзисторы Ml и М2 работают как емкости, и они разряжаются токами г _а 1 и г _а 2 .

На втором этапе на линии СИ оставляют низкий уровень напряжения, линия предзаряда находится на высоком уровне, на линию разрешения УС подают низкий уровень напряжения. Устройства Ml и М2 открыты. Устройства М5 и Мб закрыты. Токи на линии al и а2 меняют направление и значения |га1| > |га2|. Эта разница токов формирует заряд в узлах триггера.

Выходные сигналы усилителя считывания работают в противофазе во время второго этапа, в исходном состоянии на обоих выходах устанавливается нулевое значение. То есть результат логического сложения выходных сигналов может использоваться в качестве синхроимпульса усилителя считывания.

Найдем зависимость времени переключения динамического RS-триггера усилителя считывания (рис. 2а) от дифференциального напряжения на входе усилителя. Для этого построим эквивалентную схему (рис. 26).

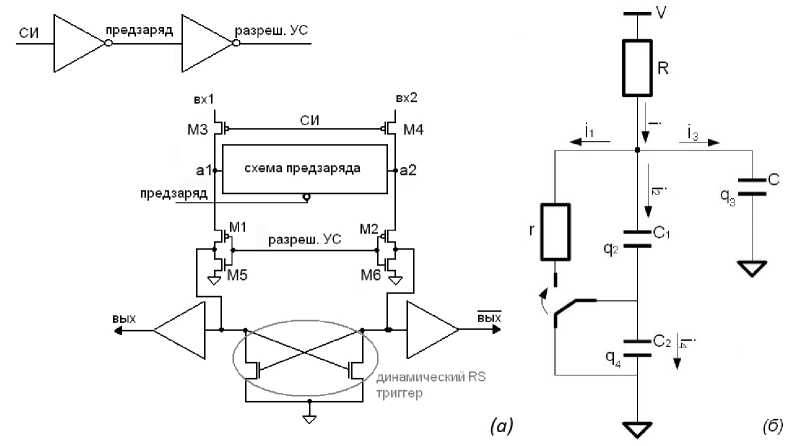
Рис. 2

Сразу после переключения разрешающего входа в 0 плечо усилителя считывания может быть представлено в виде схемы на рис. 26, где г - эквивалентное сопротивление транзисторов Ml или М2, С 1 - их эквивалентная емкость, R - эквивалентное сопротивление битовой линии, С - эквивалентная емкость битовой линии, С 2 - эквивалентная емкость динамического RS-триггера. Для токов г, г1, г₂, гз, г₄ и зарядов q₂, дз, q₄ можно записать следующую систему уравнений:

кг +а+а= v ^тг 1 = а,

< Д + г 2 + г з = г, й + г 2 = г 4 , 72 | 74 _ 73 С 1 ⁺ С2 = с .

Честный учет того, что напряжение V зависит от времени и является суммой постоянной и гармонического сигнала, приводит к громоздким выкладкам, при этом характер полученных результатов не меняется. После преобразования Лапласа и подстановки на- чальных значений заряда получаем

М + А + <& = 7 • ^Г, 1 = А, 1 1 ⁺ 1 2 ⁺ I 3 = I, 1 1 ^{+ I} 2 = Д, А ^4    !з

Ci + с2 = с, где обозначенные заглавными буквами величины являются образами соответствующих величин в (1).

Учитывая, что емкость битовой линии много больше эквивалентных емкостей транзисторов, решение может быть представлено в виде (следует помнить, что из-за сделанных упрощений полученные далее результаты не корректны при времени, сравнимом с КС\.

Д =

V • С 1 С 2      (^{s +} тс)

^СК • (^С 1 + ^С 2 ) s ( s + Т ( С1 + с2 ) ) ■

Применив следствие теоремы о вычетах, имеем

Д =

V • С 2 СК ( С 1 + С 2 )

(

С 1 + С 2 s

-

С 2

^{s +} r ( C i + C ₂ )

)

И после обратного преобразования Лапласа для заряда i4 получаем значение i4    СК Н(t) (1 С1 + С2 exp( г(С1 + С2))) ’ где Н(t) - функция Хевисайда.

Пусть т - время, за которое дифференциальное напряжение в узлах усилителя считывания достигнет порогового напряжения 14, необходимого для переключения RS в устойчивое состояние. Напряжение на емкости С2 может быть выражено следующем образом:

т

V₄ =

у 0

i4dt,

^V* = Ск^{Н (т1} (^{т + гС} 2 ^exp(-г(С 1 + С 2 )^{1- гС} 2) ■

Дифференциальное напряжение в узлах усилителя считывания запишется так:

^AV 4 = СК^{Н (т)} ( ^{т + гС} 2 ^exp(-^(С 1Дс2 )^{) - гС} 2) ⁺

^{+ Н (т}) (^{т + гС} 2 ^exp(-_Г(С 1 + С 2 )⁾" ^гС 2 ),

AV 4 = ^t.

Здесь учтено, что сопротивление входных линий в общем случае может немного различаться (на. ARV

Выразим т, при этом учтем, что показатель экспонент по модулю много меньше единицы:

_ _  Vt • СК т = 1»+^FI

·

С 1 + С 2 С 1

■

В предложенной модели не было учтено, что емкость C 2 зависит от времени, а также паразитное переменное сопротивление защелки. Но тем не менее сделанные теоретические выводы подтверждаются результатами моделирования.

Пусть на входы усилителя считывания подается напряжение с генераторов синусоидального напряжения одинаковой частоты и амплитуды. Моментальная фаза первого генератора складывается из линейно изменяющегося со временем слагаемого ш • t, где ш — частота генератора, t — время и слабо меняющегося со временем слагаемого pi. Моментальная фаза второго генератора — ш • t + p₂.

Тогда дифференциальное напряжение на входах усилителя считывания равно

6 = V (s1n(w • t + pi) — s1n(w • t + p₂)),

X          (P i - Р 2             P i +P2

0 = 2V sin(--------)cos(ш • t +-------).                            (a)

Подставим выражение (3) в (2):

Vt • CR(C i + C2)/(V •Ci)

T — ----------------------------------- ;-----------------------------.

|2 sln( ^и₂^ 2 )cos(ш • t + ^ 1 + ^ 2 ) + ^5 81п(ш • t + Pi)|

Теперь обратимся к системе, изображенной на рис. 1. Выходные сигналы с усилителя считывания собираются по ИЛИ, и через некоторую задержку Т подаются на вход синхроимпульса усилителя считывания. То есть период получившегося цикла равен: T _n — Т + т.

Учитывая, что сравнение входных напряжений усилителем считывания происходит только по отрицательному фронту синхроимпульса, то для периода цикла будем иметь

Tn

То

|2sin(Ы-) cos(ш • У T +     ) + ^ 81п(ш • У T + Pi)| i=0                             i=0

+ Т,

где То — Vt • CR(Ci + C2)/(V • Ci).

Считая pi и p2 постоянными, приведем (4) к виду

Т тп — -------------------;-----0--------------;--------+ Т,5

п—i

|2 sln(p) cos(ш • У Tj) + ^ s1n(ш • У Ti + p) | i=0

Tn+i —

| sin(arcsin( ^A ) + шт_п)|

I \             \ T^ _[_ '/I здесь

//4 sin² p + 4^5 sin² p + (^5)2

где сделаны следующие обозначения: p — (p_i — p2)/2, (p_i + p2)/2 — 0.

При численном моделировании варьировался параметр Т. Псевдофазовые траектории Tj, построенные по последним 500 значениям Tj из 100 000 отсчетов для разных значений параметра Т, представлены на. рис. 3. Когда. Т находится в лианазоне значений с 1,4• 10^—iic до 1, 7 • 10^—iic, петля подстраивается под частоту ш/ 4 ^. Когда Т находится в диапазоне значений с 4, 6 • 10^—iic ло 4, 8 • 10^—iic. петля подстраивается пол частоту ш/ Ъ ^.

Из бифуркационных диаграмм на рис. 4 видно, что при изменении параметра Т справа налево в интервале 1, 7 • 10^—iic — 1, 8 • 10^—iic наблюдается резкий переход к гармоническому режиму генерации, рис. 4а. При изменении параметра Т слева направо в интервале 4, 2 • 10^—iic — 4, 7 • 10^—ii c наблюдается бифуркационный переход через удвоение генерируемых частот, рис. 46.

Рис. 3. Псевдофазовые траектории т^, построеншые при ДЯ/Я = 0,1, То = 2,0 • 10 10с, ш = 1, 0 • 1011с- 1, ( = тт/3, (a Y Т = 1,1 • 10^-11с, (б): Т = 1,2 • 10^-11с, (в): Т = 2, 2 • 10^-11с, (г): Т = 2, 3 • 10^-11с. (д): Т = 3, 7 • 10^-11с. (с):Т = 4, 3 • 10^-11с

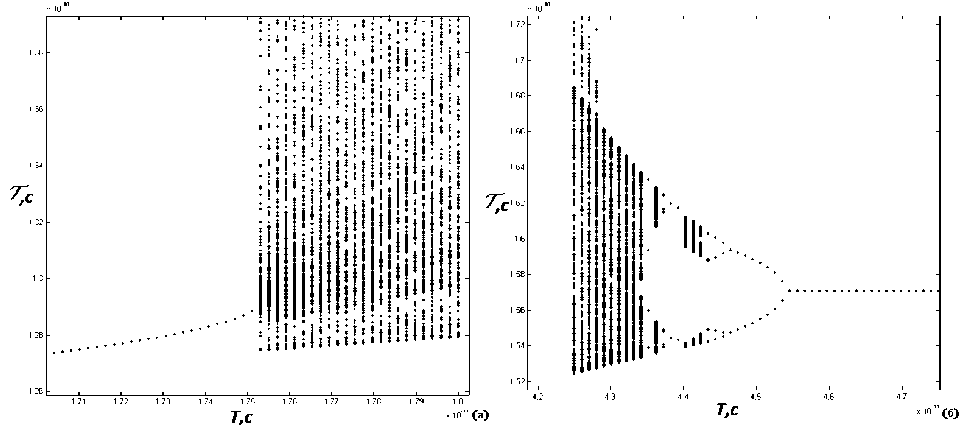
Рис. 4. Бифуркационные диаграммы в различных интервалах значений параметра Т, ДЯ/Я = 0,1,

То = 2, 0 • 10-1ос. ш = 1, 0 • 1011с-1. ( = я/3

На рис. 5 представлены результаты численной оценки показателя Ляпунова в зависимости от параметра Т, сделанной в MathLab. Для оценки показателя Ляпунова использовалось следующее соотношение [2]:

1 ^N -¹

Л = Jim    К ln |т‘"+1(т»)|.

N>го Д п=0

Графики зависимости строились исходя из фиксированного значения то, а также в качестве то бралось последнее значение, рассчитанное при предыдущем значении параметра, Т. Из графиков на рис. 5 видно, что при значениях Тс 1, 8 • 10-11с до 4, 3 • 10-11с предложенная схема является генератором хаотического сигнала.

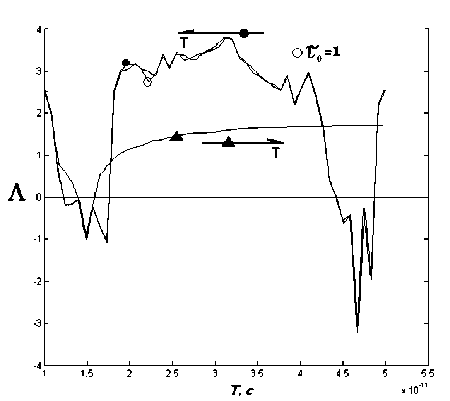
Рис. 5. Зависимость показателя Ляпунова от параметра Т, ^ R/R = 0,1, То = 2,0 • 10 10с, ш = 1, 0 • 1011с^- 1, у = тт / 3

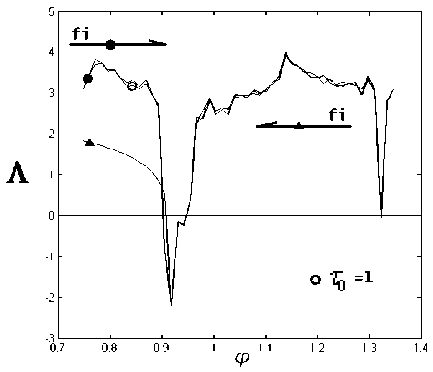
Рис. 6. Зависимость показателя Ляпунова, от ш = 1, 0 • 1011с^-1. Т = 3, 7 • 10^-11с

параметра, у. ^R/R = 0,1. Т_о = 2,0 • 10 ¹⁰с.

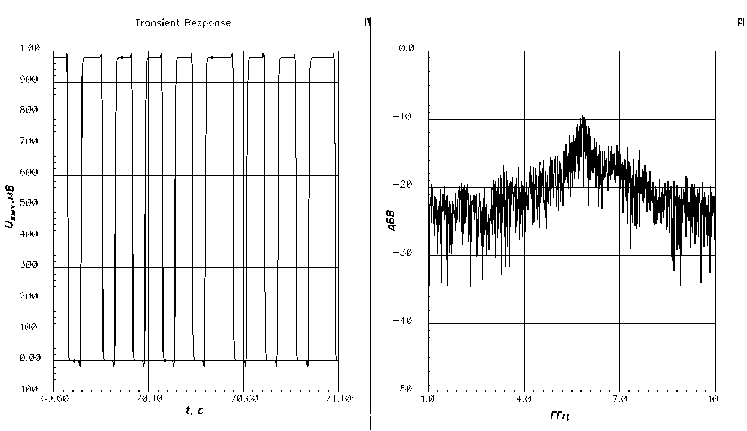
Рис. 7

Рис. 8

Также исследовалась зависимость показателя Ляпунова от параметра р (рис. 6). Методология построения графиков на рис. 6 аналогична той, что применялась при построении графиков на рис. 5.

Результаты моделирования уравнения свидетельствуют о том, что при разных соотношениях параметров разработанная схема может являться как источником хаотических колебаний, так и синхронизироваться с входными осцилляторами.

Схема предложенного генератора была реализована в схемотехническом редакторе на транзисторном уровне (технология TSMC65 пт). Размеры транзисторов подбирались исходя из следующих значений параметров уравнения (5) — То = 2, 0 • 10-¹⁰с, ш = 1, 0 • 1011с^-1, р = тг/3, Т ~ 4 • 10^-11с. Проводилось моделирование схемы генератора при помощи программы Spectre. Выходной сигнал генератора хаоса и его спектр представлен на рис. 7.

Также была построена бифуркационная диаграмма модели генератора на транзисторном уровне (рис. 8). Плавным изменением мощности инверторов в петле генератора хаоса, увеличивалось значение параметра Т. В результате строился график зависимости локальных минимумов и максимумов частоты генератора хаоса от параметра Т.