Genetic algorithm control of model reduction passive quarter car suspension system

Published Online February 2019 in MECS DOI: 10.5815/ijmecs.2019.02.02

The principle capacity of vehicle suspension system is to limit the vertical speeding up transmitted to the traveler which straightforwardly gives street comfort [1]. Ordinary passive suspensions utilize a spring and damper between the auto body and wheel gathering, speaking to a trade-off between clashing execution measurements, for example, traveler comfort, street holding, and suspension redirection. The primary target of suspension system is to diminish movements of the sprung mass (vehicle body) to street aggravations [2]. A passive suspension can store vitality by means of a spring and to disseminate it by means of a damper. Its parameters are for the most part settled, being accomplished a specific level of trade-off between street taking care of, stack conveying and ride comfort [3]. The execution of the passive suspension relies upon the street profile. The controller of such system is closed-loop form, so that the performance, have been studies by many researchers. There are many methods, like, Proportional-Integral-Derivative(PID), which is the most-used feedback control design in [3,4] but still, the desired specifications (peak or overshoot values and settling time) are not meet, and needs more tuning, In light of the linear control of the PID controller, it was an inability to control this system.

The Linear Quadratic Control (LQR) strategy actualized to the dynamic suspensions system for a quarter auto model. Comparison between passive and active dynamic suspensions system are performed by utilizing distinctive sorts of street profiles [5,6,7]. While in [8,9], proposed a fuzzy logic control (FLC), to improve the road disturbances performances and this reduce the steady-state error and increase the accuracy, but still needs more time for reaching the final value . In [10,11] Proportional Integral and Derivative and Sliding mode control were produced to enhance and track system reaction, but still there are many problems in transient response, more overshoot. In [12,13] Conducted a similar trial check execution of the dismissal of street disturbance influence by H- infinity and enhanced LQR controller for the quarter auto suspension system. Likewise, in [14,15]presented another control approach for the passive quarter auto suspension system utilizing neural systems and LQ adaptive control to relieve vibrations and ensuing adjustment to street unsettling influences. In [16] a strong pole position for a dynamic suspension quarter-auto model through parameter dependent control was proposed which guarantees to the uncertain loop system a pre determined pole-position inside a hover on the left - hand of the complex plane for system strength. In [17,18] adaptive neural system (ANN) is proposed to make the controller strength against deliberate vulnerabilities, which discharge the modelbased necessity of the sliding model control, and the weighting network is balanced online based by Lyapunov work. In [19,20] an optimal review control of a vehicle suspension system going on a harsh street is examined. The suspension system is optimized regarding to ride comfort and street holding inclinations, including increasing speeds of the sprung mass, tire diversion, the results demonstrate that the optimal control enhances all parts of the vehicle suspension execution while requiring less power. Model order reduction has well-known advantages in large scale simulation, analysis and control design, and has been widely examined and utilized, in some papers [21, 22,23]. In this paper, comparison amongst PID, LQR, and FLC with minimum rules, H2 controller and Genetic Algorithm Control are presented. Whatever section II, which clarifies the model depiction and reduction of it, section III gives an understanding to the controllers plan, while results comparison are presented in section IV, last the general conclusion is made in section V.

M X = -K (X -X )-b (X -X )

s s          s     s        us       s     s        us

MX us = K s ( X s - X us ) + b s ( X s - X us ) - K ( X us - r )

• II. Quarter Car Modeling

The quarter auto demonstrates is set up utilizing interconnections of masses, springs and dampers. Fig. 1 demonstrates a two-degree-of-freedom a passive quartercar model system. In this model, the sprung and unsprung masses corresponding to the one corner of the vehicle, (Ms) is the mass of the auto body,(Mus) is the un-sprung mass of the haggle gathering, (ks) is the spring consistent in the suspension system, (bs) is the dashpot steady (speaking to the safeguard) and (kt) is the spring steady of the tire, since damping in the tire is typically very small, it is neglected in [5].The wheel after the car hits a unit bump, that is (r) represents unit-step input road disturbance, (xs) the car body travel(displacement) is following up on the mass (Ms), (Xus) the wheel travel (displacement) is following up on the mass(Mus) .

The direct conditions of movements of the vehicle system after using Newton's law, we can demonstrate, the following dynamics equations by Dowds and Dwyer in [1] and [24,25,26]:-

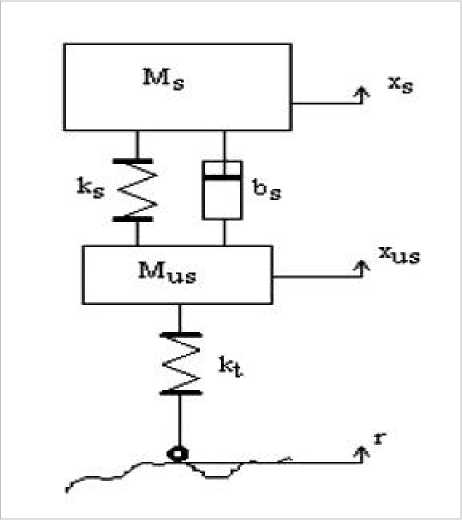
Fig.1. Shows a two-degree-of-freedom a passive quarter-car model [1]

These equations give the following transfer function relating Xs to r.

Xs

Kt ( bS + Ks )

r  MsMusS4 + (Ms + Mus) bS3 + ((Ms + Mus) Ks + MsKt) S2 + bKtKsS + KsKt

In this paper (the values of these parameters are taken from Gene et. al. in [27], where: -

Ms=20 Kg, Mus=375Kg, Ks=130331.58N/m, Kt=997264N/m and bs=9799N.s/m, so that the Transfer function can be written as: -

Xs____________________1.31*106( S +13.3)__________________ r " S4 + 516.1 S3 + 5.685 *104S2 +1.307 *106S +1.733 *107

By using MATLAB tool, figure 2 show the step transient response of the equation (3). It can be seen that the maximum overshot is (Mp=30%) and settling time (Ts=0.348sec).

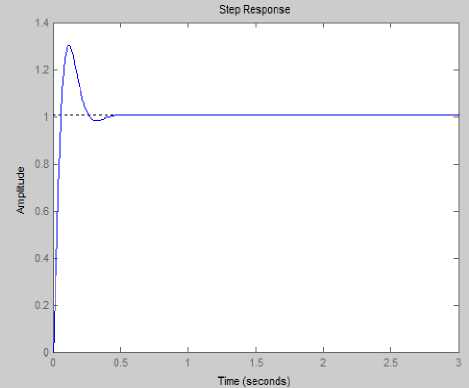
Fig.2. Shows the transient response of original system

Working with lower-order models can improve investigation and control plan, in respect to higher-arrange models. Less complex models are likewise less demanding to comprehend and control. High-arrange models acquired by linearizing complex models or from different sources can contain states that don't contribute much to the dynamics of particular interest to your application. Along these lines, it can be valuable to decrease demonstrate arrange while saving model attributes that are critical for your application. There are many methods for model reduction, in this paper, using moment matching method [28], where separate dominate po\es from no-dominant and keeping, which poles are very close to imaginary-axis (these effectively poles) ,so that the second-order reduced Transfer function is:-

Xs         1024

" S ² + 23.133 S + 1024

There are no large differences between original and reduced order systems, where both have the same overshot and settling time, Figure 3 shows transient response of original and reduced order systems. For simplicity in design and analysis, equation (4) can be used instead of equation (3).

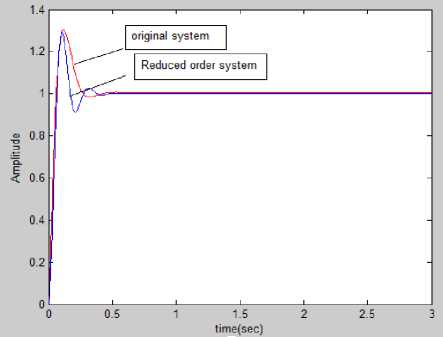
Fig.3. Transient response comparisons between original and reduced System

• A.    PID Controller

  The most prevalent linear control system that has been utilized by specialists in the plan of the dynamic suspension system is based on (PID) controller. Here using three term parameters proportional, integral and derivative, there is no steady-state error in the system under control, so that can use only(PD) controller to improve the dynamics effect (Mp and Ts). Using the classical tuning method and table of Ziegler and Nichols [4], we get the controller parameters, KP=156.15 and Kd=0.7586.

Fig. 4 shows the transient response with PID controller as seen from fig. the (Mp=12%) and (Ts=0.0132), so this type of controller needs more tuning to reach good response.

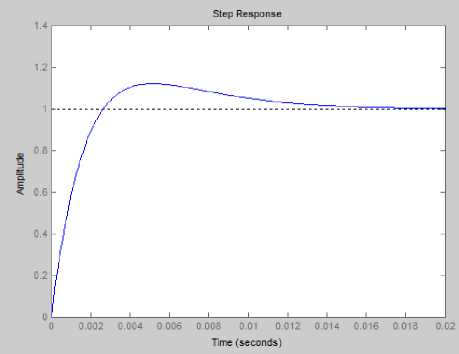
Fig.4. Shows the transient response with PID controller

• B.    Linear Quadratic Control (LQR) controller

The LQR calculation reduces the measure of work done by the control systems specialist to improve the controller. The architect still needs to determine the cost work parameters, and contrast the outcomes and the predefined plan objectives. Frequently this implies controller development will be an iterative procedure in which the designer judges the "ideal" controllers created through simulation and after that modifies the parameters to deliver a controller more steady with design objectives. The state-equation of system is: -

III. Quarter Car Controllers

In the previous years, different control procedures have been proposed by various scientists to enhance the exchange off between ride comfort and street dealing, in the following, some of these control approaches that have been reported in the literature will be briefly presented. The purpose of using controllers in Quarter car, to improve dynamic behavior, when the car subjected to road disturbances. The design requirements depend on the behavior of car suspension, so that no overshoot and less settling time. It necessary to chose (Mp=0) and (Ts=0.01sec).

XX = Ax + Bu y = Cx

Where the model matrix, input and output vectors are:-

- 1024   - 23.133

C = 1024  0|

The feedback control law that minimizes the value of the cost is:-

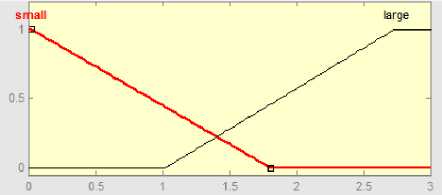
Fig.6. Shows the inputs membership functions

U=-Kx(t)

To find the values of K=[K1 K2], must solving, Riccati differential equation The design procedures can be found from [29],let :-

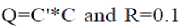
Using LQR MATLAB statement, the values of K1= 2372 and K2= 49.5. Fig. 5 shows the transient response with LQR controller, (Mp=8.17%) and the settling time is (Ts= 0.103sec). These values are out of design requirement.

Fig.7. Shows the output membership functions

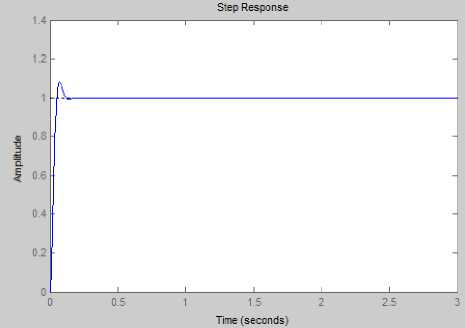
Fig.5. Shows the transient response with LQR controller

Fig.8. Shows rule-based for fuzzy control

• C.    Fuzzy logic controller (FLC)

  

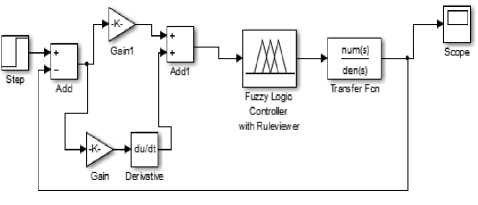
  Fig.9. Shows the simulink-diagram of fuzzy control system

  
  

  A fuzzy rule base has a very significant effect on the control strategy in a fuzzy controller, in other words it defines the strategy of the controller. The fuzzy logic controller used in the passive suspension has two inputs and one output, the desired road disturbance. The control system itself consists of three stages: fuzzification, fuzzy inference machine and defuzzification [30]. In this approach using minimum rules and these uses the true value of input road disturbance (low and high), to generate a result in the fuzzy set for car body displacement (small and large). The inputs to fuzzy, are error (e) and derivative of (e). The input, output membership functions and the rules based are appear in Figs. (6,7,8) respectively. While Fig. 9 shows the simulink diagram of fuzzy control system. The same values of KP=156.15 and Kd=0.7586, can be chosen, figure (10) shows the transient response of fuzzy controller, where (Mp=0), but still (TS=0.146sec) is not meet design specifications.

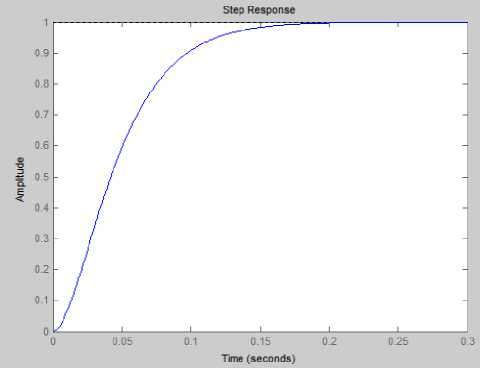
Fig.10. Shows the transient response with fuzzy-logic controller

• D.    H2 controller Design

The outline of straight suspension controllers that underline either traveler solace or suspension deflection. The controllers in this area are composed utilizing straight H2 method [31]. As is standard in the H2 system, the execution goals are accomplished by means of limiting weighted transfer function standards.

The standard H2 optimization problem is the problem of choosing the compensator Ce in the block diagram of Fig. 11 such that it: -

• 1.    stabilizes the closed-loop system

• 2.    minimizes the H2-norm of the closed-loop system (with w as input and z as output).

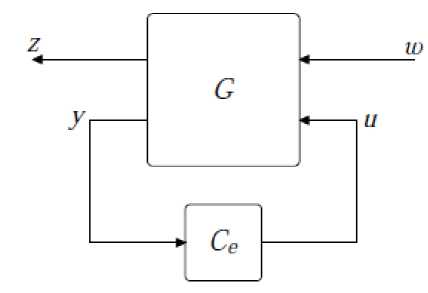
Fig.11. Shows the H2 control system

Where (G) is the passive Quarter Car Suspension transfer function and must be putted in state-space form, refer to equation (6). Weighting capacities (W1, W2) fill two needs in the H2 system: They permit the immediate examination of various execution destinations with a similar standard, and they take into consideration recurrence data to be joined into the investigation. For more details on H2 control design, refer to [32]. ( W 1 and W 2) weighting filters that may be used to modify the design, and so that, plays the role of design parameters. This choice of W 2 reduces the Weight on the input over the frequency band where the disturbances are large. This allows the gain to be large in this frequency band. To do so, find a stabilizing controller K that minimizes the H2 norm. Assume the following weights: -

W1 = 0.1*(s+1000)/(100*s+1), W2=0.1. The H2 controller was designed by MATLAB statement (H2SYN), the gain controller (K) can be calculated and the transient response after compensation is shown in Fig. 12. The system response is without any overshoot, while Ts=0.434sec is very large, so this method needs more trial and error for choosing the proper values of weighting filters.

• E.    Genetic Algorithm (GA) controllers

(GA) is type of search algorithm inspired by biology. They are based on the idea of evolution. A (GA) will be used to find the right weights and topology for a given problem. Recently, intelligent based techniques such as neural network and genetic algorithm have been applied to the passive and active suspension system [33]. In (GA) a populace of irregular genotypes is made and their fitness is assessed. The fitness work is diverse for each test. Here the fitness work is the way of Quarter Car Suspension System gets to the objective.

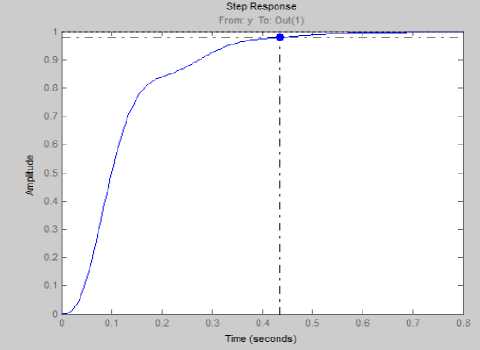
Fig.12. Shows the transient response with H2 controller

The GAs more than once changes a populace of individual arrangements. At each progression the GAs select individual at arbitrary from the present populace to be guardians and utilization them to create the youngsters for the people to come. Over progressive generation, the populace develops toward an ideal arrangement. Three fundamental steps of GAs [34]:

1-Selection: selects the individuals, called guardians that add to the people to come.

2-Crossover: joins two guardians to frame youngsters for the people to come.

3-Mutation:  apply arbitrary changes to singular youngsters.

For the outline of the GA-based PID controller, see Fig.13, initial an underlying populace of the GA is produced by irregular, this contains double strings, where a string speaks to the corresponding, proportional, integral and derivative gains (Kp, Ki, Kd). The target work is required to assess the best PID controller for the framework. A target capacity could be made to discover a PID controller that gives the littlest overshoot, fastest rise time or quickest settling time. In any case, keeping in mind the end goal to join these destinations it is expected to outline a target work that will limit the execution lists of the control framework. Every chromosome in the populace is passed into the target work each one in turn. The chromosome is then assessed and relegated a number to speak to its fitness. The (GA) utilizes the chromosome's fitness value to make another populace comprising of the fittest individuals. The process of optimization is calculated by maximization of the fitness function (F) which is the mean error between the current value of the system output and the desired reference:

T

MSE = ¹ J( e ( t ))² dt

^T 0

Fitness =----

MSE

method PID-GA, with [9], using (FLC) and by Jin in [35], using parameters optimization, it is clear that the proposed method gives great improvement in design requirements.

In this paper, GA parameters are chosen according to the trial and error method as follows:

Population size=50; Crossover rate= 0.2; Mutation rate=0.01; Maximum generation =120 Roulette wheel selection method is considered with uniform mutation and arithmetic crossover. Fig. 14 shows the response of the Passive Quarter Car Suspension System of PID-GA controller, here all design specifications are satisfied, noovershot, and (Ts=0.011sec). The parameters of the PID are: - Kp = 1599.7678, Ki= 475.7819 and Kd = 7.832.

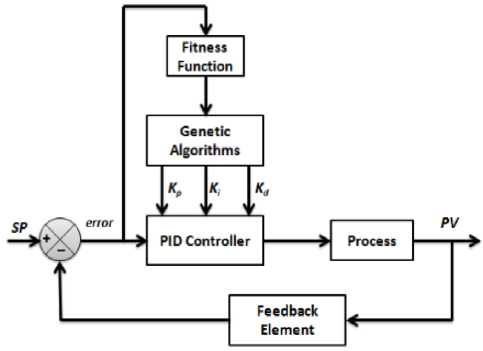
Fig.13. Shows (GA) based-PID controller

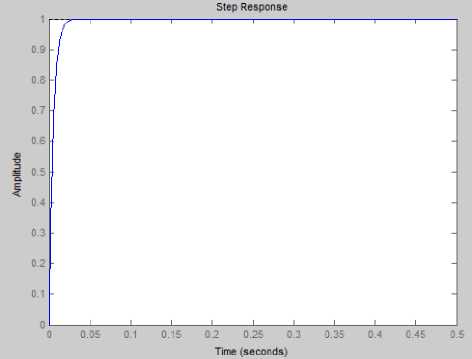
Fig.14. Shows the transient response with (GA) controller

• IV.    Results Comparison and Discussion

The reactions of all gave controllers are contrasted regard with settling time, maximum overshoot, and steady state error, as appeared in Table I. It is seen that GA gives preferred outcomes over different strategies, yet GA requires 51.86 seconds computational time to tune the PID controller. When comparing the proposed

Table 1. Comparison between all controllers

Controller types	Settling time(sec)	Max. overshot%	Steady-state error
PID	0.0132	12%	0
LQR	0.103	8.17%	0
FLC	0.146	0	0
H2	0.434	0	0
PID - GA	0.011	0	0

• V.    Conclusion

The passive suspension framework is an open loop control system. It just plans to accomplish certain condition as it were. The normal for uninvolved suspension are settling and can't be balanced by any mechanical part. Subsequently, the execution of the passive suspension relies upon the street profile. different methods for controlling the system are used some of these (FLC and H2 ) are satisfied one specification max.overshot,but settling time     out of design requirement ,(PID and LQR),needs more tuning to improve (MP and TS). PID-GA appears to offer the most satisfied result, where (MP=0%) and (Ts=0.011sec). This basic linear quarter-vehicle system has a few focal points: Due to its straightforward structure and low dynamic order, it offers an instinctive comprehension of the vertical powerful response. In addition, it offers a good reason for controller design. Finally, the reason for this paper is to research the ideal outline of a quarter auto passive suspension framework utilizing a GA optimization calculation, keeping in mind the end goal to limit the applied disturbances and vibrations.

Acknowledgment

The author would like to thank Mustansiriyah University ( Baghdad – Iraq for its support in the present work.