Genetic Algorithm For Designing QMF Banks and Its Application In Speech Compression Using Wavelets

Published Online May 2013 in MECS DOI: 10.5815/ijigsp.2013.06.01

Quadrature Mirror Filter (QMF) banks are most commonly used in many signal processing applications such as: sub-band coding of speech and image signals [10][11][12], audio, image or video processing and its compression [13][14][15], transmultiplexer [16], design of wavelet bases and communication systems [17] and others applications. Therefore, several techniques have been presented for designing the QMF banks based on linear and non-linear phase objective function. In [2], author has introduced the theory of two-band linear phase QMF banks and design a family of filters using non-linear optimization based Hooke and Jeaves optimization algorithm [19] and a Hanning window [2]. A linear optimization method has introduced in [19] for designing M-band QMF banks, this method consists in iteratively adjusting the pass-band to minimize the reconstruction error.

Thereafter, several new iterative algorithms [20] [21] [22] [22] [23] [24] [25] have been developed using window technique to optimize QMF banks design.

However, the used window functions can be classified into two categories: the first category is fixed length window such as Hamming, Hanning and Rectangular window; the main lobe width is controlled only by window length. The second category is adjustable length window; the main lobe is controlled by the window length and one or more additional parameters such as the shape window used for controlling the spectral characteristics [1].

In the above context, in this work a real-coded GA is exploited for designing a QMF banks based on adjustable windows length. The paper is divided into four sections, as follows. Section 1, discusses the analysis and synthesis using two-channel QMF banks. Section 2, presents the proposed methodology for designing QMF banks using real-coded GA. Section 3, attempted to explain the principle of speech compression using DWT. Finally, comparative study between the optimized wavelet filters using GA and the others known wavelets is carried out in section four.

• II.    TWO-CHANNEL QMF BANKS

The basic structure of two-channel QMF bank is illustrated in figure 1. The analysis step consists in split the input signal x(n) into two frequency bands by a low-pass analysis filter H(z)and a high-pass analysis filter H(z). Then, the obtained subbands are down sampled by factor of two. In the synthesis step, each subband is up-sampled by factor of two, and then passing through low-pass synthesis filter G(z) and high-pass synthesis filter G(z). Finally, the obtained sub-bands are recombined to reconstruct signal y(n).

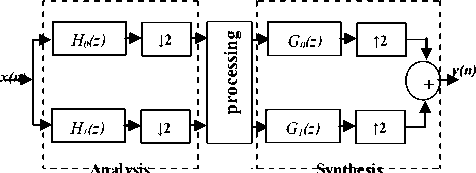
Figure 1. Two-channel Quadrature mirror filter banks.

The input output relationship of the two-channel QMF bank in the z-transform [9] is given in (1):

Y ( z ) = 1 [ H о ( z ) C o + H 1 ( z ) С , ] X ( z )

+ 2 E H o ( - z ) C o + H i ( — z ) С , ] X ( — z )

From the above equation, the reconstructed signal Y ( z ) composed by two terms each multiplied by the original signal X ( z ) . The first term, called the distortion transfer function, and the second term is the aliasing transfer function, which can be eliminated by the condition given in (2):

H , ( z ) = H ₀( - z )

C o ( z ) = H ₀( z )                           (2)

C , ( z ) =- H ₀( - z )

Then, the equation (1) becomes:

Y ( z ) = 1 [ H О ( z ) - H О ( - z ) ] X ( z )                (3)

From equation (3), it is clear that the complexity of the two-channel QMF bank design is reduced to design one only low-pass filter H ( z ). Now, Let H ( z )a finite impulse response filter (FIR) of even order N and a frequency response given in (2):

2 ® n

Ho(ej) = Ho(c)e 2(4)

The transfer function ( T ( e ' ” ) ) of the two-channel QMF bank using equation (3) becomes:

T (ej) = — {| Ho( ej )|2 +| Ho( —-'’)[}

The perfect reconstruction is possible if equation (6) is satisfied [2].

IH o( e■ )|‘+| Ho( —-")|' = 1

If the above condition is not satisfied, then a reconstruction error occurred. This error can be minimized by a simple real-coded genetic algorithm.

pass-band ripple ( 5  ) and stop-band ripple ( 5 ).

ps

Therefore, the filter based on Kaiser Window must be designed to meet the smaller of the 5 and 5 ps constraints:

⁵ = min ( ⁵ p , ⁵ s )

The Kaiser Window of length N is given in (8):

■ ( n )

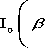
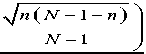
I o ( в )

o <  n <  ( N — 1)

otherwise

Where I_o ( . ) is a zero th order modified Bessel function of the first kind, which may be easily, generated using the power series expansion expressed as follow:

+^

I o ( - ) = 1 + ^

k = 1

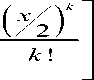
The values of window shape (β) and window length (N) could be chosen to meet any set of design parameters ( 5 , ■ , ■ ):

ps

o.1,o2 ( A - 8.7 )

A > 50

в =

N =

0.4

o.5842 ( A - 21 )

+ o.o7886(A - 21) 21 <  A <  5o

A - 8

2.285( " - ■ )

A < 21

Where, A = - 2o log₁₀ ( 5 ) and ( "  , ■  ) are

respectively the pass-band and stop-band transition.

The low-pass filter design with Kaiser Window will have a cutoff frequency ( ■ ) centered at [ "  , ■ ]:

■

c

■p + "s

III. RREAL-CODED GA BASED ON QMF DESIGN

In this paper, different QMF banks are designed using a simple real-coded GA based on Kaiser Window. However, the Kaiser window depends on two parameters: the window length (N), and the shape window parameter (β) which controls the spectral characteristics of the window. Large values of β reduce the window side lobes and therefore result in reduced

In this case, the window parameters are completely determined. Now, the cutoff frequency ■ and the window shape (β) can be optimized such that the objective condition given in equation (6). In what follows, a simple real-coded GA is exploited in order to optimize the cutoff frequency ■ and the window shape (β).

Figure (2) illustrates the flowchart of the real-coded GA used for optimizing the cutoff frequency to_c and the shape window (β) of Kaiser.

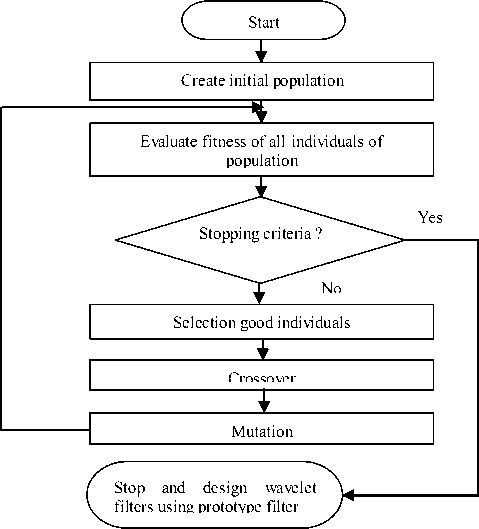
Figure 2. A flowchart of QMF banks design using GA.

• 3.    GA stop if error is less than the tolerance ( err       <  tol ) or when the maximum number

iIi=1,2,...., n of generations is reached. Otherwise GA repeats the following steps.

o Selection good individuals : this operation consists in selecting individuals from the population for reproduction based on the relative fitness value of each individual. It can be performed by Elitist selection function: The best individuals of each generation are guaranteed to be selected.

o Crossover: to apply the crossover operator, two chromosomes are randomly selected from the population. Then the two chromosomes are chopped into two parts at the crossover point and they exchange their parts. For example :

Parent 1  = [ ^ в ] Parent 2  = [ ^₂ Д ]

Children1 = [ ®,Д ]            Children 2 = [ ^ ₂ в ]

o Mutation randomly alters each gene with a small probability, typically less than 10%. This operator introduces innovation into the population and helps prevent premature convergence on a local maximum.

o Replace the current population with the new population.

The different steps of the adapted GA for designing wavelet filters are:

new population =

C^[^ _c 1

A ] . ^

^[^ c 2   ^в 2 ^] ₂

1. Initialization of the population of chromosomes (set of randomly generated chromosomes).

l ^[ ^ cn   ^e n ^] n )

o Go to step 2.

• 4.    Stop and design wavelet filter using prototype filter.

• 2.    Evaluation     of     the     fitness     functions

Where, to_d/₁ = 1,2,..., n P i// _{= 1},2,..., n are respectively the initial values of the cutoff frequency and the Shape of Kaiser Window.

f ( to. , 6X. . _o for each individual. j \ ci*> ri /Ii = 1,2,..., n

Design prototype filters using Kaiser Window (equation (8)) and compute the magnitude responses (MRC,„=,2):

MRCi ,„L2........= |e”'|«- = j(13)

err    = Mr/ - MRC\(14)

iIi=1,2,....,n          |i |

Where, MRI is the magnitude response in the ideal condition (MRI=0.707) [20] and erris iIi=1,2,...., n the fitness function.

• IV.    SPEECH COMPRESSION USING DWT

The Wavelet Transform (WT) has emerged as a powerful mathematical tool in signal processing area; it provides a compact representation of a signal in timefrequency domain. The Discrete Wavelet Transform (DWT) is a special case of the WT; it consists in decomposing a signal in too many functions by a function called a mother wavelet. The mother wavelet is dilated by powers of two and translated by integers. Specially, the signal x ( t ) in time domain can be expressed as follow:

X ( t ) = ^2 ^+1^ d ( j , k ) ^ (2 - j t - k ) j =1 k =—i

+ 22 ^a ( L , ^k )Ф (2 ^— L t — k )

k =-i                                         (15)

Where, ^(t) and Ф(t) are respectively the mother wavelet function and the scaling function. a(L, k) is the approximation coefficients at scale L and d(j,k) is the detail coefficients at scale j . The approximation and detail coefficients are calculated using the following formulas:

L го

a ( L,k ) = 2 2 J x ( tф (2 - ^L t - k ) dt k,L ^X       (16)

—^

j ^

d ( j , k ) = 2 2 J x(t ) ^ (2 ^jt - k ) dt  j,k ^X       (17)

—^

In [3], it was shown that the wavelets concentrate speech information (energy and perception) into a few neighboring coefficients. Therefore, after applying the DWT to the signal and the thresholding, many coefficients will be stetted zeros (have negligible magnitudes) and others retained. Compression is achieved by efficiently encoding the obtained coefficients.

The speech compression algorithm using wavelets can be divided in three major steps [3], [4], [5], [6], [7]: Applying the DWT to the original speech signal, thresholding the obtained coefficients and applying the inverse DWT to reconstruct the signal. More precisely the figure 3 illustrates the process of speech compression based on DWT, it is involves a number of different steps:

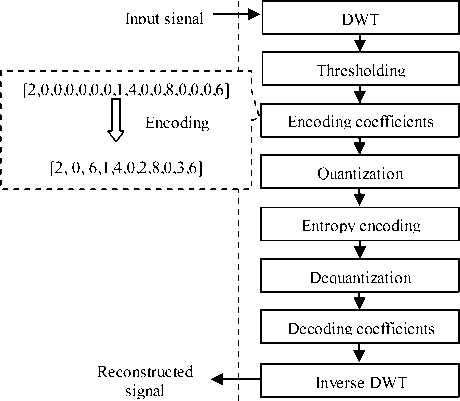
Figure 3. Principal block diagram of speech compression using DWT.

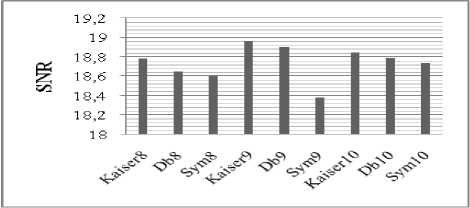
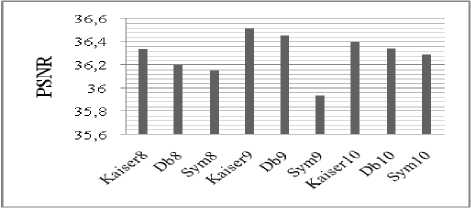
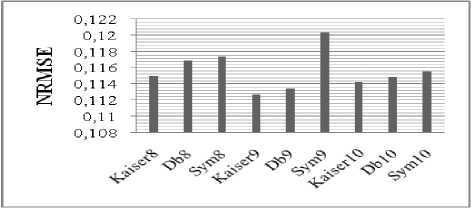
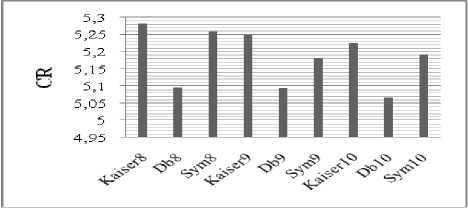
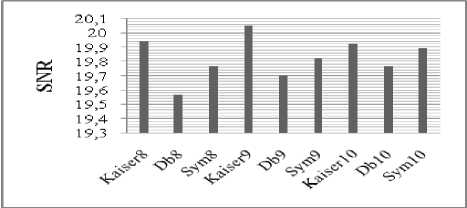
Step 1: Choosing the mother wavelet, the decomposition level and applying the discret DWT to the original speech signal. Here, the choice of wavelet mother is a very important step in speech compression based on wavelets. In [8], it was shown that the choice of an optimal mother wavelet depend on several different criteria, the main objective is to maximize the signal to noise ratio (SNR) and minimize the reconstructed error variance, the adequate decomposition level is up to scale five[8]. In this work, different mother wavelets filters are designed using the proposed algorithm. The choice of the optimal mother wavelet for speech compression is based on the CR, SNR, PSNR and RMSE.

Step 2: After applying the DWT, the obtained coefficients are thresholded. Generally, there are two ways to computing the threshold values; global thresholding and level depending thresholding. When the thresholds values are calculated, typically hard or soft thresholding can be applied to truncate the coefficients with negligible magnitudes. Then the obtained wavelet coefficients are encoded. In this paper, two byte are used to encode one or string values of zeros [3]: One byte to indicate the start of a sequence of zeros in the wavelet coefficients and the second byte representing the number of consecutive zeros (see example: figure 3).

The encoded coefficients are converted to others coefficients, with fewer possible discret values by a quantization algorithm such as: uniform, scalar or vector quantization algorithm. To remove the redundancy caused by the quantization, entropy encoding have been used such as: Huffman encoding or arithmetic encoding. The output bitstream of entropy encoding are multiplexed and transmitted.

Step 3: For reconstruct the speech signal, the received bitstream demultiplexed and entropy decoding is used to extract the quantized coefficients. Finally, an inverse quantization is applied to extract the encoded subbands followed by inverse DWT.

• V.    TESTS AND RESULTS

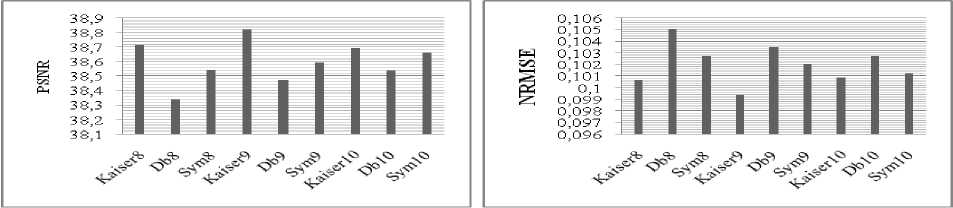
In this section, a MATLAB program has been written for implement the real-coded GA for QMF banks design described in this paper. The designed QMF banks are exploited as mother wavelets in speech compression algorithm based on DWT. In order to show the effectiveness of the optimized wavelets filters in speech compression, a comparative study of performance of the developed wavelets (see appendix) and others known mother wavelets (Daubechies and Symlet) is performed. The obtained results are calculated using the following formulas:

Signal to Noise Ratio (SNR): snr =    ^ ^{x (} n )      (18)

^1 x ⁽ n ) ^- y ⁽ n )|²

Peak Signal to Noise Ratio (PSNR):

PSR = 10log₁₀

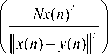
Normalized Root Mean Square Error (NRMSE):

I (x ( n ) — y ( n ))² NRMSE =   ^{( V}

( x ⁽ n ) ^- M x ^{( n} ) )

Compression Ratio (CR):

CR =

size of original signal size of compressed signal

Where, x ( n ) and y ( n ) are respectively the original and the reconstructed speech signal, N is the length of the reconstructed speech signal and ^ ( n ) is the mean of the speech signal.

In the simulation, the optimal settings of the GA as follow in table 1:

TABLE 1. REAL-CODED GA PARAMETERS USED FOR QMF BANKS DESIGN.

parameters	values
Coding	Real
Population size	40
Maximum number of generations	30
Size of chromosome	2
Cutoff ( to c )	0.45 - 0.60
Shape Kaiser window(β)	4.54 - 8.96
Tolerance (tol)	10-5
Fitness Function	fitness =Minimize (|err-tol|)
Selection Technique	Elitist selection.
Probability of selection	0.5
Method of mutation	Random.
Mutation probability	pmut = 0.1
Method of crossing	One point crossover
Probability of crossover	pcross =0.5
Stopping criterion	Maximum number of generations or fitness ≤tol

TABLE 2. COMPARAISON OF PERFERMANCE USING DAUBECHIES AND SYMLET WAVELETS

Source waveform files	Wavelet filters	CR	SNR	PSNR	NRMSE
sx37.wav	Kaiser8	5.2835	19.9408	38.7144	0.1007
	Kaiser9	5.2491	20.0503	38.8240	0.0994
	Kaiser10	5.2248	19.9233	38.6969	0.1009
	Db8	5.0956	19.5683	38.3420	0.1051
	Db9	5.0942	19.7040	38.4776	0.1035
	Db10	5.0664	19.7664	38.5401	0.1027
	Sym8	5.2597	19.7692	38.5428	0.1027
	Sym9	5.1808	19.8227	38.5963	0.1021
	Sym10	5.1912	19.8931	38.6668	0.1012
sx22.wav	Kaiser8	4.4686	18.7862	36.3387	0.1150
	Kaiser9	4.4366	18.9616	36.5141	0.1127
	Kaiser10	4.3943	18.8450	36.3974	0.1142
	Db8	4.3523	18.6474	36.1999	0.1169
	Db9	4.2904	18.9032	36.4556	0.1135
	Db10	4.3121	18.7913	36.3438	0.1149
	Sym8	4.4223	18.6043	36.1568	0.1174
	Sym9	4.4011	18.3853	35.9378	0.1204
	Sym10	4.3562	18.7394	36.2919	0.1156

(a)

(b)

(c)

(d)

(e)

(f)

(g)                                                         (h)

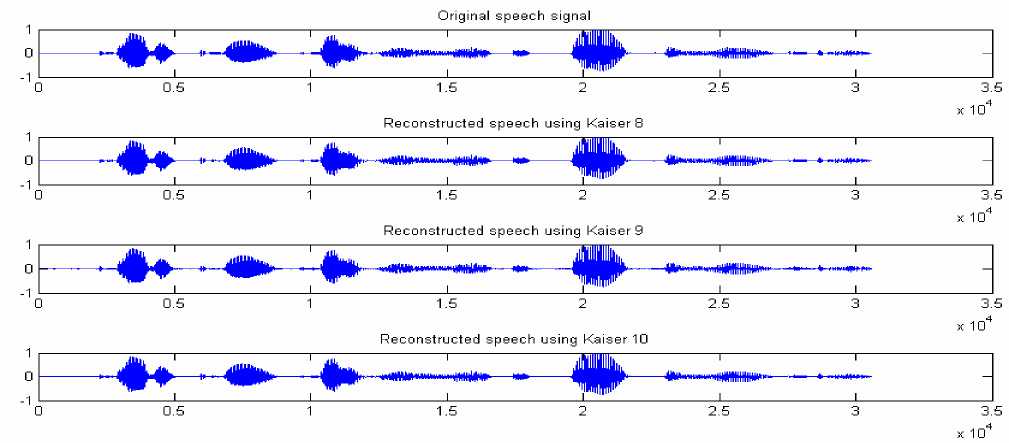
Figure 6. Original and reconstructed speech signal with different Kaiser Windows.

Figure 6 shows time domain representation of original speech signal (sx37.wav: “Critical equipment needs proper maintenance”) and its reconstructed versions using optimized wavelet filters: Kaiser 8, Kaiser 9 and Kaiser 10. It is clear that the reconstructed speech signals are similar to the original.

• VI.    CONLUSION

In this paper, a real-code genetic algorithm is used to design QMF banks based on Kaiser Window. The optimized filters as used as mother wavelets for speech compression based on discret wavelet transform. The spectral characteristics of the prototype filters are optimized to minimize the reconstruction error. The simulation results confirm the efficiency of the optimized wavelet filters on speech compression. From the comparative study of the developed wavelet filters and others known wavelets mother, it is also observed that the optimized wavelets using GA outperforms others wavelets already exist in term of CR, SNR, PSNR and NRMSE.