Genetic Centralized Dynamic Clustering in Wireless Sensor Networks

Published Online July 2015 in MECS DOI: 10.5815/ijcnis.2015.08.01

Wireless sensor networks (WSNs) are used in many application fields, such as habitat monitoring, commercial applications, military surveillance, forest fire detection, home applications, hazardous environment sensing and smart spaces, inventory tracking, , general engineering, underwater applications, disaster management, biomedical health monitoring, animal tracking, seismic detection, etc [1]. Indeed, according to [2] WSNs are listed as one of the key technologies of the internet of things. They are listed, also in [3], to be one of the new technologies that will change the world and our life,

Nodes (or motes or Sensors) are physical entities characterized by: (i) a processor with a very limited processing capabilities; (ii) a battery with a limited energy, often irreplaceable and not rechargeable; (iii) and a transceiver [4]. A node may contain, also, an analog to digital converter (ADC), a memory, a global positioning module, etc.

The nodes can be deployed in monitoring areas in order to gather multiple types of information (e.g., light, humidity, wind, temperature,...) and then transmit the gathered information to the Sink sensor node (Access Point or gateway), generally using multi-hop routing strategy [5] or by using one-hope routing strategy . In turn, the sink transmits the collected information to the end users.

WSNs may be deployed in inaccessible areas (volcano, the bottom of the sea ...) [6], and as it could often be difficult to replace batteries, extending the lifetime of the WSN is very important.

In the literature, many papers show that the source of highest energy consumption in the sensor node is the transceiver [7], making strategies which minimize the use of the transceiver is very attractive. Several techniques can be used to save energy, among which clustering.

The Clustering consists in grouping sensors in several clusters, so that each cluster has a single cluster-head and several cluster-members. In each cluster, the clustermembers gather information on the sensed area and send it to the cluster-head. In turns, the cluster-head processes the data received from its members and send it to the sink. Fig. 1 shows a clustered wireless sensor network with three clusters, each cluster contain only one cluster-head and at least one cluster-member. Each cluster-member sends the gathered information to its cluster-head, which in turn send it to the sink.

In a clustered WSN, data collected by the sensors is communicated to its cluster-head, for data processing and redundancy elimination. Therefore, sensors communicate data over short distances in each cluster (to cluster-heads), so that the energy spent in communication will be lower than that spent with sensors communicating directly to the sink [8, 9].

Clustering can be static or dynamic. In a static scenario, the numbers of cluster-heads is fixed and tend to exhaust their energies rapidly, which make this clustering unsuitable for WSNs [10]. In fact, the network becomes nonfunctional in the absence of cluster-heads. In the presence of dynamic clustering, the clusters change over the time, equalizing the energy consumption across all nodes and, thus, extending the network lifetime.

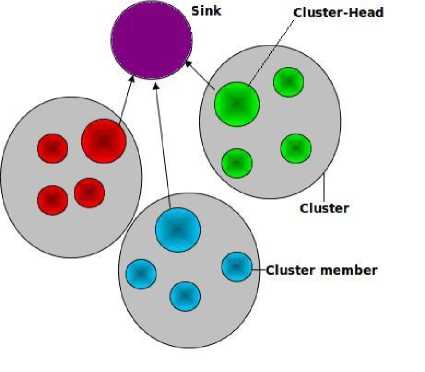
Fig.1 Clustered WSN.

In this paper, our goal is to maximize network lifetime (defined as the time interval from the nodes' deployment to the instant at which a given percentage of deployed nodes die [6]) by minimizing the average energy consumption of all nodes. In order to do this, all nodes can be promoted to the role of cluster-heads. In order to reach this goal and guarantee full coverage (i.e., the clusters are spread over the entire network), we rely of on the use of a genetic algorithm (GA), which determines, in each cycle, whether or not a node can be chosen to play the role of a cluster-head.

• II.    R elated W orks

The idea of using clustering has been adopted by many authors. The linked clustering algorithm (LCA) was one of the first approaches [11]. In the LCA algorithm, each node has a unique ID. In this algorithm a node play the role of cluster-head if its ID is the highest one in its neighboring.

LEACH (Low-Energy Adaptive Clustering Hierarchy) is the most popular clustering algorithm for WSNs [10]. LEACH allows a fixed percentage of nodes to become cluster-heads (namely, 5% of the nodes) and leads to the creation of clusters in a distributed way, with the nodes taking autonomous decisions. Each node decides to become a cluster-head with probability p . A node which does not become cluster-heads determines its cluster by choosing the nearest cluster-head.

On average, LEACH provides low energy consumption and a uniform energy distribution among the nodes. However LEACH has also some drawbacks. Because of the probabilistic selection of the cluster-heads, a node with a very low energy can be selected as cluster-head. Moreover, since the selection of cluster-heads is probabilistic, the chosen cluster-heads may be placed in the same area, so that a good coverage cannot be guaranteed: in fact, some nodes will be disconnected from the network (i.e., they will not attach to any clusterhead). Moreover, the use of a fixed percentage of clusterheads may lead (network-wide) to higher energy consumption, as the number of cluster-heads depends on several factors, such as node spatial density [12,13].

EEHC is a randomized and distributed clustering algorithm, whose goal is to maximize the network lifetime [14]. This algorithm is executed in two levels. In the first level, denoted as “initial” volunteer nodes, which do not belong to any cluster, may decide to be clusterheads with probability p and they announce their decisions to their neighbors. The nodes that do not receive an announcement, within a specified time interval t , become forced cluster-heads. In the second level, denoted as “extended”, the clustering algorithm is recursively repeated to form hierarchical clustering, where new cluster-heads are selected from the already formed cluster-heads, until a final base station is reached.

In [15], the authors consider a GA and adapt, on the basis of software services, its parameters to determine the energy consumption and, therefore, extend the network lifetime. In [6], the authors proposed a GA-inspired routing protocol (GROUP): in particular, they use GA and simulated annealing (instead of the greedy chain) to select routing paths efficiently.

• III.    S ystem M odel

The conditions and assumptions behind the considered network model are compliant with those considered in [10] for LEACH. More precisely, they can be summarized as follows:

• 1.    The base station is fixed, is not energy-constrained, and has a high computing capacity.

• 2.  All  the nodes deployed are energy/power-

• constrained and homogeneous.

• 3.  The data processing power is very low with

respect to the power required to transmit and receive data.

The nodes' radio communication specifications are set as in [10, 4, 6, 16]. In particular, we assume that the radio module dissipates: E ₌ = 50 nj/bit in transmission and reception circuitry; and O_am == 100 pJ/bit/m² in the transmitter amplifier. Considering free space communications, in order to transmit a k -bit message over a distance d (dimension: [ m ]) a node consumes the following amount of energy:

ETx (k, d) = Eelec X k + Oamp X к X d 2     (1)

When receiving a k -bit message a node consumes the following amount of energy:

E rx ( k ) = E elec X k              (2)

• IV.    T he P roposed approach

• A.    The Problem Presentation

In a clustered WSN, if a few cluster-heads are used, then most of the nodes are likely to have a long transmit radio range to send the collected data to their clusterheads and this tends to quickly deplete their batteries' energies. If a large number of cluster-heads is used, this leads mostly to a one-hop network (most nodes are cluster-heads and must reach the base station in one hop): this consumes also quickly the battery energy [4, 11, 16].

The best clustering strategy consists in optimizing (i) the number of cluster-heads and (ii) their positions. In particular, a node can be promoted to cluster-head according to several parameters: its residual energy, its distance to the sink, and the sum of the distances to its cluster-members. This suggests the use of GAs to find the optimal combination of these parameters.

• B.    The Proposed Algorithm

In this paper, we consider dynamic clustering, i.e., reclustering is considered to avoid early death of clusterheads. The proposed GA is executed at the sink (i.e., it is centralized ), due to the needed computing capacity, and the obtained results (in terms of clustering configuration) are communicated to the nodes. At each re-clustering round, each node can then be either a cluster-head or a cluster-member. This centralized approach is expected to overcome the main limitations of LEACH, where the number of cluster-heads is fixed and their spatial distribution is arbitrary, i.e., there is no coordination [10].

In order to use a GA, a WSN needs to be “codified”. In particular, we use a binary representation, in which each node is represented either by 0 (if it is a cluster-member) or by 1 (if it is a cluster-head). Each codified network is called a “chromosome”. A set of chromosomes is called a “generation”.

The used GA is based on exploration and exploitation of the entire research space using an evolutionary strategy; it helps us to find an optimal combination of clusterheads, cluster-members and their distributions in the monitoring area, among many combinations existing in the research space, making the energy consumption and the network coverage, optimal. Each potential solution is characterized by a value called fitness, which determines the optimality of solutions. In correspondence to a generation, the GA keeps the best chromosomes and drops others according to their fitness function. Each chromosome, in fact, represents a potential solution. The GA then applies the following genetic operators to generate new offsprings [17].

Selection : The selection process is used to choose the best chromosomes from a generation. In our simulation, the roulette wheel algorithm is used to perform the selection.

Crossover : To apply crossover, we choose arbitrary two chromosomes from a generation, we choose, also, two random positions in the chosen chromosomes and we used the two point crossover, to generate two new offsprings that will belong to the next generation.

Mutation : The mutation is used to avoid the super chromosome problem. It means if one chromosome is selected many times in the same generation, the crossover will not produce new chromosomes, since the parents are the same chromosome. Hence, the mutation is used to change, in each chromosome, an arbitrary bit. Several tentative have been performed so to come up with the best-run GA parameters in terms of runtime and convergence. The best crossover and mutation probabilities are 0.75 and 0.2 , respectively.

As mentioned above, each chromosome is then evaluated with a fitness function which attributes a higher chance to the best solutions to survive.

The fitness of a candidate chromosome can be expressed as follows:

Fitness = f ( NNN , NCH , DNCH , RECH )    (3)

·

Where:

• ■    NNN is the number of networked nodes;

• ■    NCH is the number of cluster-heads;

• ■    DNCH is the sum of the distances between the cluster-members (CMs) and their cluster-heads (CHs), i.e.,

DNCH = X X Distance(CH ,CM )   (4)

i e {CHs} j e {CMs}

• ■    RECH is the sum of residual (cumulative) energy at the cluster-heads (dimension: [^mW]), i.e.,

RECH = X Residual energy at the CH,      ⁽⁵⁾

i e{CHs}

In order to optimize the proposed clustering mechanism, we consider the following (heuristic) fitness function:

Fitness = ( NNN ) “ 1 +

NNN Y² . _____ +

NCH )

(10 ³ x RECH ) “ ³ + DNCH “ 4

Where: the exponential parameters { a }4₌₁ need to be properly optimized; the fraction NNN / NCH represents the average cluster dimension; the multiplicative term 10 ³ used for RECH properly weighs

The energy dimension. By trial and error, the best fitness function (i.e., the best configuration of the exponents {a }4=i) turns out to be:

Fitness = ( NNN ) 6 +

NNN У

NCH J

+

(10 3 x RECH ) ² + DNCH

C. Performance Analysis

In this subsection several experiments are performed using Matlab to validate the proposed GCDC Algorithm (GCDC for Genetic Centralized Clustering Algorithm). In order to validate the proposed clustering approach, we carry out a simulation-based performance analysis, considering different scenarios, by varying the node spatial density, the number of nodes, and the sink position. In each scenario, a given number of sensors is randomly deployed in a square monitored area, with side length 100 x 100 m 2 .

The sink, placed within the network, runs the GCDC algorithm and informs the sensors of the decided clustered configuration. After receiving the decision, each node knows if it is a cluster-head or a cluster-member. The GCDC algorithm is periodically executed by the sink in order to avoid that a node death compromises network connectivity. We assume that all nodes have batteries with initial energy equal to 0.25 J, scattered randomly within 100 x 100 m ² . The dimension k of the messages to be transmitted is set to 1000 bits plus 50 bits control packet.

Fig. 2.(a) show, the first case study, of a wireless sensor network compound of 100 homogenous nodes, scattered randomly in sensor field of 100 x 100 m ² . The sink is placed at the center of the field.

Fig.2.(a) Wireless sensor network with 100 nodes.

Fig. 2.(b) show, also, a wireless sensor network compound of 1000 homogenous nodes, deployed randomly in a monitoring area of 100 x 100 m ² . The sink is at the center of the field.

Fig.2.(b) Wireless sensor network with 1000 nodes

We assume that random “events” (e.g., acoustic signal detection, motion detection, etc.) happen in the monitored area: in particular, each random event is detected by its nearest neighbor, which needs to report this observation to the sink.

In all considered scenarios, the performance of the GCDC algorithm is compared with that of LEACH. Two values of the initial number of nodes in the WSN are considered: 100 (low node spatial density) and 1000 (high node spatial density).

Fig. 3.(a) and Fig. 3.(b) show the same scattered network of 100 nodes after applying GCDC and LEACH algorithm, we can conclude from the figures that using GCDC algorithm offer better connection of the network than LEACH algorithm, which fixes at advance the number of the cluster-heads at 5% and does not guarantee a uniform distribution of the Cluster-heads in the network, unlike GCDC which use GAs to determine the appropriate number and position of CHs to cover the entire network and to consume less energy.

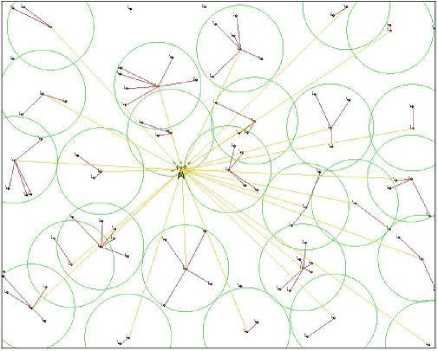
Fig.3.(a) WSN of 100 nodes after applying GCDC

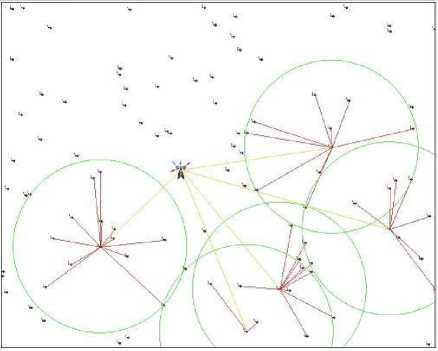
Fig.3.(b) WSN of 100 nodes after applying LEACH

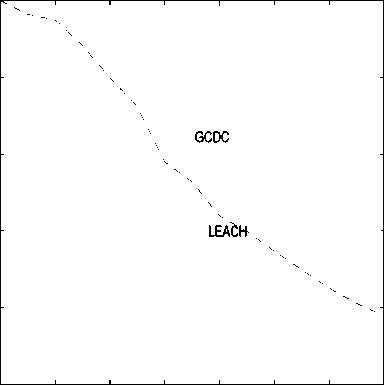
In Fig. 4.(a) and Fig. 4.(b), the residual network energy is shown as a function of the simulation time (expressed in event number), considering two values for the initial number of nodes: (a) 100 and (b) 1000.

It can be observed that GCDC algorithm allows saving more energy than LEACH. The energy saving is not relevant at the beginning, whereas it becomes more significant as the time passes by. This is due to the fact that the GCDC algorithm updates the network clustered topology very efficiently. This behavior is more pronounced in the scenario with 100 nodes (low node spatial density).

0.25

0.2

2> ф ш 0.15

я

0.05

0        1        2        3       4        5       6        7

Evenment Number                  _x^q*

Fig.4.(a) Network residual energy as a function of the simulation time (in terms of event number). The initial number of nodes in the network is set to: (a) 100.

0.25

0.2

Е* ф ш 0.15

я 3

0.05

О 0        1        2        3       4        5       6        7

Evenment Number                  _x^q*

Fig.4.(b) Network residual energy as a function of the simulation time (in terms of event number). The initial number of nodes in the network is set to: (b) 1000.

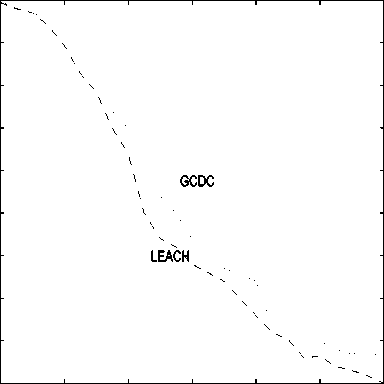
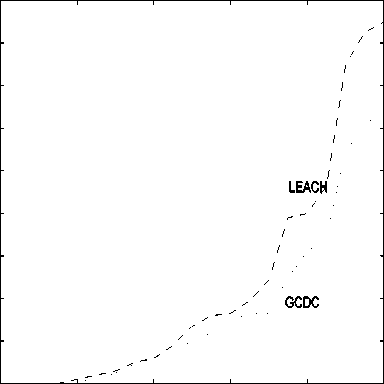
In Fig. 5.(a) and Fig. 5.(b), we investigate the network connectivity evolution considering (a) NNN (i.e., the network coverage) and (b) the number of dead nodes, as a function of the simulation time (in terms of event number).

In both cases, the initial number of nodes in the WSN is set to 100 (low node spatial density).

From the results in Fig. 5.(a), it can be observed that the number of nodes connected (i.e., becoming cluster members or heads) by the GCDC algorithm is larger than that guaranteed by LEACH. This is more evident at the beginning of the simulation, when all nodes (having full battery energies) could be connected, whereas the improvement brought by GCDC reduces for advancing simulation time, as a larger and larger number of nodes die.

The performance difference is due to the fact that LEACH a priori sets the number of CHs to 5%of the total number of nodes without identifying their positions: this likely leads to overlapped clusters (i.e., two CHs may be close to each other), leaving other nodes (without a sufficiently close CH) disconnected. The GCDC algorithm does not determine a priori the number of CHs but, rather, the GA determines the optimized number of CHs, along with their positions, to cover the entire monitored area efficiently. In Figure 5.(b), the number of dead nodes (after energy depletion) is shown: as expected from Figure 5.(a), the death rate with GCDC is lower than that with LEACH, owing to the clustering procedure which takes into account the nodes residual energies.

® 01

ф У ф

Ф о

LEACH

GCDC

ф

i ®

900 ф oi I 850 ф ф a 800 ф т о £ 750

j 700 ф z

601-------1-------1-------1-------1-------1—

0.5     1      1.5     2     2.5     3

Evenment Number

3.5     4     4.5     5

x10

550 0         2         4         6         8         10        12

Evenment Number                 v,n4

Fig.5.(a) Network connectivity evolution, in terms of NNN , as a function of the simulation time (in terms of event number). The initial number of nodes in the WSN is 100

Fig.6.(a) Network connectivity evolution, in terms of NNN as a function of the simulation time (in terms of event number), the initial number of nodes in the WSN is 1000.

о 30

§25

Ф w

ф v о

LEACH

GCDC

m

Ф □

0 0

I 120 Q. Ф о 80 c

S 60

20 0

Evenment Number

x10

0           2           4           6           8           10

Evenment Number                  _x^q4

Fig.5.(b) Network connectivity evolution, in terms number of dead nodes, as a function of the simulation time (in terms of event number). The initial number of nodes in the WSN is 100.

In Figure 6, the network connectivity evolution, considering (a) NNN (i.e., the network coverage) and (b) the number of dead nodes as functions of the simulation time (in terms of event number), is investigated in a scenario with 1000 initial nodes (high node spatial density).

Fig.6.(b) Network connectivity evolution, in terms of dead nodes, as a function of the simulation time (in terms of event number), the initial number of nodes in the WSN is 1000.

By comparing the results in Figure 5.(a) with those in Figure 6.(a), it can be concluded that the performance improvement, in terms of NNN , brought by GCDC is more pronounced in dense network. In particular, since, according to the results in Figure 6.(b), the death rates of GCDC and LEACH are approximately the same in the beginning of the simulation and after that the GCDC algorithm shows its effectiveness compared to LEACH, it means that the GCDC is very efficient in re-clustering the topology in order to guarantee a high level of connectivity to the surviving nodes.

• V. C onclusion

In this paper, we have presented a novel clustering algorithm, denoted as Genetic Centralized Dynamic Clustering (GCDC), in which we use the genetic algorithm, as tool, to define the best number of clusterheads and their locations to ensure the minimum energy consumption and the best coverage in the network. The proposed clustering algorithm is re-executed periodically at the sink, due the necessity of the big capacity of computation, to define a new combination of clusterheads and cluster-members, to avoid the early extinction of the unlucky chosen nodes to play the role of clusterheads in the previous round, using several parameters presented in section IV. The performance of our algorithm has been compared with that of the most used clustering algorithm (LEACH), which fixes at advance the number of the cluster-heads, which do not guarantee a total coverage of the network.

The obtained results show that the proposed clustering algorithm reduces, significantly, the (network-wide) energy depletion rate and guarantees a better network coverage, compared to LEACH. An interesting research direction consists in applying the proposed GA-based clustering algorithm to duty-cycled Wireless Sensor Networks.

• [11]    O. Boyinbode, H. Le, and M. Takizawa, “A survey on clustering algorithms for wireless sensor networks”. International Journal of Space-Based and Situated Computing , vol. 2, pp. 130-136. 2011.

• [12]    S. Jin, M. Zhou, and A. S. Wu, “Sensor network optimization using a genetic algorithm ”. In Proceedings of the 7th World Multiconference on Systemics, Cybernetics and Informatics , pp. 109-116. July 2003.

• [13]    B. B. Lokesh, N. Nalini, “Genetic Algorithm Based Node Fault Detection and Recovery in Distributed Sensor Networks”, I.J. Computer Network and Information Security , vol.12, pp. 37-46, September 2014.

• [14]    S. Bandyopadhyay, and E. J. Coyle, “An energy efficient hierarchical clustering algorithm for wireless sensor networks”. In proceedings INFOCOM 2003. Twenty-Second Annual Joint Conference of the IEEE Computer and Communications . Vol. 3, pp. 1713-1723, IEEE. April 2003.

• [15]    A. Norouzi, F. S. Babamir, and A. H. Zaim, “A New Clustering Protocol for Wireless Sensor Networks Using Genetic Algorithm Approach”, Wireless Sensor Network , vol. 3, pp.362-370, 2011.

• [16]    K. Mekkaoui, A. Rahmoun, and G. Ferrari, “Genetic Centralized Dynamic Clustering in WSN”, In proceedings CIIA 2015. 5th International Conference on Computer Science and its Application , pp.503-511, Springer, 2015.

• [17]    J. Holland, “Genetic algorithms”, scientific American , vol. 267, pp.66—72, 1992.