Genetic spectrum assignment model with constraints in cognitive radio networks

Published Online June 2011 in MECS

The demand for the wireless spectrum has been increased enormously with the growth of wireless communication and multimedia applications. But the existing static spectrum allocation policies have caused the low utilization of the wireless radio spectrum according to the research results of FCC(Federal Communication Commission). As an effective way to improve the spectrum utilization and solve the current spectrum scarcity problem, cognitive radio is becoming one of the research focuses recently. In cognitive radio networks, the cognitive users(secondary users) can access the licensed spectrum which is not occupied by the licensed users(primary users). Cognitive radio transceiver has the abilities to sense the ambient environment, select the spectrum assignment strategy dynamically, and use the spare spectrum to establish wireless communication

Manuscript received January 0, 2011; revised June 0, 2011; accepted July 0, 2011.

Project supported by Fundamental Research Funds for the Central Universities.

efficiently, thereby achieve the optimal performance for wireless communication system[1].

With the development of cognitive radio technologies, the dynamic spectrum access problem has become one of the key technologies in cognitive radio networks. The spectrum resource can be shared by the primary users and secondary users by spectrum overlay and spectrum underlay paradigms[2]. In spectrum overlay paradigm, secondary users can access the spectrum opportunistically when the licensed spectrum is not occupied by the primary users. In the underlay paradigm, the spectrum can be shared by the primary users and secondary users simultaneously, but the interference caused by the access of secondary users should be controlled within certain limits. In this paper, the opportunistic spectrum assignment problem with the acknowledgement of the states of licensed spectrum is analyzed. In order to get better performance of the system utilization, genetic algorithm is applied in the spectrum assignment problems.

Genetic algorithm is one of the typical intelligent algorithms that imitates the natural evolution, and is widely applied in the optimization problems. Genetic algorithm, which has a good search capability, is introduced into cognitive radio networks to optimize performance and fulfill the various needs in wireless communications applications. In this paper, the spectrum assignment model based on genetic algorithm is analyzed. In order to avoid the interference constraints problems that exist in the genetic spectrum assignment model for cognitive radio networks, an improved genetic spectrum assignment model with the consideration of interference constraints is discussed.

The rest of the paper is organized as follows. In section II, the related works on spectrum assignment problems are described. The spectrum assignment model in cognitive radio networks in analyzed in section III. The genetic algorithm based spectrum assignment model is presented in section IV, the interference constraints is further analyzed, and the improved genetic spectrum assignment model and quantum genetic spectrum assignment model are discussed in detail. The simulation results of different spectrum assignment model are shown in section V. Finally, we conclude the paper in section VI.

• II.    R ELATED WORKS

The spectrum assignment model in cognitive radio networks is discussed. The graph color spectrum assignment model for cognitive radio networks was analyzed in [3-5]. The genetic algorithm based control module for wireless communication system was designed, and optimization of the parameters in cognitive radio system was realized in [6-7]. The selection of the population in genetic algorithm for the optimization problem in cognitive radio environment was discussed in [8], the adaption of the population could reduce the time that caused to reach the optimal decision. Z. Zhao et al. made explorations into the genetic algorithm based cognitive radio decision engine, and the wireless radio parameter optimization based on the quantum genetic algorithm is designed in [9]. The spectrum assignment problem of centralized network based on quantum genetic algorithm was also discussed in [10][11]. In order to reduce the encoding redundancy of genetic algorithm, only the non-zeros elements in the channel availability matrix were encoded. Besides, the quantum genetic algorithm based spectrum assignment model could get better performance. The immune genetic algorithm was applied in the optimization problems of cognitive radio decision engine in [12], and it could achieve better hillclimbing capability and stability compared with conventional genetic algorithm. J. Zhou proposed the parallel immune genetic algorithm model for adaptive modulation and spectrum assignment in cognitive radio networks in [13], and the proposed spectrum assignment algorithm has better global searching capability and faster convergence speed.

Due to the flexibility of the genetic algorithm, the different communication requirements of the spectrum assignment and optimization problem are discussed by genetic algorithms. The genetic algorithm was applied in the multi-objective optimization problem of cognitive radio networks in [14][15], the influence of bit error rate (BER), out-of-band (OOB) interference and overall throughput were considered jointly. And the problems of population adaptation, variable quantization, variable adaptation in the optimization of cognitive radio networks were discussed in [16], the improvements to enhance the convergence time and system performance were proposed. The multi-objective resource allocation problem for the OFDM based cognitive radio network was also analyzed in [17], the fitness function was composed of the requirements as minimum transmission power, maximum throughput and the minimum BER.

• III.    S PECTRUM A SSIGNMENT M ODEL OF C OGNITIVE R ADIO N ETWORKS

Assuming the available spectrum can be divided into non-overlapping orthogonal channels, N cognitive users competing for M orthogonal channels. Cognitive users can get acknowledge of the ambient information through spectrum sensing technologies. The spectrum assignment model can be abstracted as channel availability matrix L, interference constraints matrix C, channel rewards matrix B, assignment matrix A.

• 1)    Channel availability matrix

L ={ l nm | l nm ∈ {0,1}} N×M is a N by M binary matrix representing the channel availability. If l nm =1, channel m is available for user n ; l nm =0, channel m is occupied by primary users, and not available for cognitive user n .

• 2)    Interference constraint matrix

C ={ c ij | c ij ∈ {0,1}} N × N is a N by N binary matrix representing the interference between two cognitive users when they occupy the same channel. If c ij =1, interference will exist when cognitive user i and j sharing the same channel. Whereas, c ij =0, cognitive user i and j can share the same channel. The interference between cognitive users depends on the distance and transmitting power.

• 3)    Channel rewards matrix

B ={ b nm | b nm >0} N×M is a N by M binary matrix representing the rewards of cognitive user n occupying channel m , usually using the maximum bandwidth or throughput.

• 4)    Assignment matrix

A ={ a nm | a nm ∈ {0,1}} N×M is a N by M binary matrix. If a nm =1, channel m is assigned to cognitive user n , otherwise a nm =0. The assignment matrix must meet the interference constraints, that is two cognitive users that interfere with each other can’t share the same channel, i.e.

a im a jm C ij = 0     "  i , j = 1, L , N , m = 1, L , M (1)

Here we choose the product of assignment matrix A and channel rewards matrix B as the system utility. The spectrum assignment that maximizes the system utility is chosen as the desired spectrum assignment, so the target function can be expressed as

NM

A ^* = m _Λ ax ∑∑ a _nm b _nm            (2)

• n = 0 m = 0

where Λ is the set of feasible assignment strategies that satisfy (1).

• IV.    G ENETIC S PECTRUM A SSIGNMENT M ODEL WITH C ONSTRAINTS

The spectrum assignment problem of cognitive radio networks can be considered as an optimization problem with constraints. The conventional genetic algorithm based spectrum assignment model can achieve the spectrum assignment strategy with high fitness value, as expressed in (2), but the co-channel interference constraints can’t be satisfied directly. A constraints-free procedure is proposed in [10] to obtain the spectrum assignment strategy without co-channel interference.

For channel m , finding cognitive users i and j that satisfy c ij =1, and checking whether the spectrum assignment elements of user i and j for channel m are both 1. If the corresponding elements are both 1, one of them is set to be 0 randomly, and the other assignment element keeps unchanged. After this procedure, the chromosome which corresponds to spectrum assignment strategy can satisfy the interference constraints condition described as (1).

Although this additional constraints-free procedure can achieve the feasible spectrum assignment strategy, it is required to perform the constraints-free procedure as long as the population of genetic algorithm is updated. As the update of the population is the most important part in the evolution of genetic algorithm, and it is performed repeatedly, thus it would bring extra computational complexity. Besides, the constraints-free procedure will also reduce the fitness value of the chromosomes in the population.

In order to reduce the computational complexity, an improved genetic spectrum assignment model with the consideration of interference constraints is proposed. The population of genetic algorithm is divided into two sets, the feasible spectrum assignment and the randomly updated spectrum assignment. The penalty function is added to the fitness function, and the fitness value of chromosomes which dissatisfied with the interference constraints are reduced, thus the feasible spectrum assignment with the target of maximizing the system utility can be achieved through evolution. This proposed scheme also applies for the quantum genetic spectrum assignment model. The details of genetic spectrum assignment model and quantum genetic spectrum assignment model are described as follows.

• A.    Genetic spectrum assignment with constraints

• 1)    Encoding

As the corresponding elements of assignment matrix should value 0 when the elements of channel availability matrix L value 0.Thus if all elements of L are encoded, large redundancy will be caused. Therefore, only the elements of L that value 1 are encoded here. Fig.1 shows an example of encoding of matrix L.

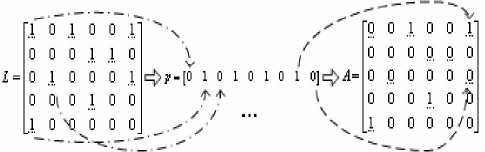
Figure 1. Encoding of chromosome

• 2)    Population

The size of population is determined according to the number of cognitive users. Then, the population is divided into sets of feasible solutions and randomly updated solutions. Feasible solutions are the assignment strategies that satisfy the interference constraints of spectrum assignment problem. In this paper, the constraints-free procedure is done to the half of chromosomes from the population, and it can also be regarded as the restoration of feasibility of solutions. No additional procedure needs to be done to the randomly updated chromosomes from population. Although the feasibility randomly updated chromosomes is uncertain, but the diversity of the chromosomes is guaranteed by the random update.

• 3)    Fitness function

According to (2), the maximization of system utility is chosen as the target of the spectrum assignment problem. The penalty function is added to the fitness function according to the interference constraints of spectrum assignment in cognitive radio networks as (3). The value of penalty function is 0 when the corresponding spectrum assignment is feasible, and penalty function will be a large value when the assignment falls out of the feasible district.

NM     NNM f = y Vb b - ОУУ Yacc..  (3)

nm nm                    im jm ij n =1 m =1                  i=1 j =1 m =1

where a is penalty factor, which is used to control the influence of penalty function to the fitness function.

• 4)    Genetic operator

The core of genetic algorithm usually includes the selection, crossover and mutation operators. The fitness values of the chromosomes in population are firstly calculated, the chromosome with largest fitness value will replace the one with small fitness value by the selection operator. In order to maintain the good characteristics of the population, the crossover operator is applied, two randomly selected chromosomes from the population are chosen as the parent chromosomes, the locations of crossover operator are randomly generated according to the length of chromosome, then crossover of the parent chromosomes is carried out at probability p c . Although selection and crossover operators can accomplish the evolution of population, they can’t guarantee the good genes that do not appear in the population can be found. Therefore, mutation operator at a certain probability is necessary to generate new individuals. Here the mutation operator is performed at probability p m to the randomly selected chromosome at randomly generated location. Thus, good characteristics of the population are reserved to some extent, and the randomness of population is guaranteed with the help of genetic operators.

• (5 ) Stop criteria

The stop criteria of genetic algorithm are checked at each cycle. If they can’t be satisfied, step (3) and (4) are continued. The number of maximum iteration and the difference of fitness value are used as the criteria to determine the termination of genetic algorithm. The flow chart of the genetic spectrum assignment algorithm is shown in fig.2.

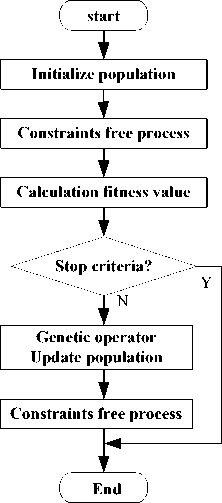
Figure 2. Flow chart of the genetic spectrum assignment model

• B.    Quantum genetic algorithm spectrum assignment with constraints

Quantum genetic algorithm is the combination of quantum computation and genetic algorithm. The quantum states are used as the basic units of information, and the quantum state vector is used to accomplish the encoding of genetic algorithm. The chromosomes in the population are evolved by the rotation of the quantum bits. Instead of the crossover and mutation operators of conventional genetic algorithm, the quantum genetic spectrum assignment model can achieve the optimized solution faster and get better performance. The details of the spectrum assignment model based on quantum genetic algorithm are elaborated as follows.

• 1)    Quantum bits encoding

Similar to the genetic spectrum assignment model, only the non-zero elements in the channel availability matrix L is encoded in order to avoid large redundancy. In conventional genetic algorithm, the genes of the chromosome are definite bits 0 and 1, while in quantum genetic algorithm the genes are composed of the quantum bits, and the quantum bits defined here can be any linear superimposed state besides the basic state 0 and 1.

| ф >= a|0 >+ j\1 > (4) where a and j are the probability amplitude of the state 0 and 1, and normalization condition should be satisfied as i a2+i в2=i

Similar to the genetic spectrum assignment algorithm, the chromosome in the population can be encoded as qk

kkk an  a21  K чj j* K

where q ^k is k ^th chromosome in the population, and 1 <  к <  l p , l p is the number of the chromosomes in the population, which is also defined as the size of population, l c is length of the chromosome. As the information contained in each gene is in no longer definite, different from the conventional genetic model, the operation to the genes would have influence on its possible states.

• 2)    Initialization of the population

Similar to the proposed genetic spectrum assignment model described earlier in this paper, the population of quantum genetic algorithm here is also divided into two groups: the chromosomes that satisfy the interference constraints by the constraints-free procedure and the randomly updated chromosomes. Here the initial values for the quantum bits in the population are all 1 2 .

• 3)    Observation

By the observation of the chromosomes from the population, definite solutions can be achieved. In the t ^th iteration, a group of solutions can be achieved, x = ( x 1 , x ² , K , x ^{l p} ) , where x is an l p by l c binary matrix, the elements x ^k = ( x k , x ₂ ^k ,K _{, x l} ^k _p ) , and each bit of x ^k is determined by the probability amplitude of quantum bits | _a^k |² and jp^. |²■ During observations, a random variable is generated, if it is greater than the probability amplitude |ak |², then x * = 1, otherwise x k = 0 .

• 4)    Evaluation

The fitness function defined as (3) is used to calculate the fitness value of each solution in the population, and the solution that has largest fitness value is reserved as the best solution, b = ( b 1 ,b ₂,K, b c ) ■ The best solution defined here is temporary, and it is updated during the evolution.

After the evaluation, if the stop criteria are satisfied, the quantum genetic algorithm is terminated, and spectrum assignment strategy that corresponds to the reserved best solution is chosen as the final spectrum assignment strategy. The maximum number of iterations and the difference between the maximum and minimum fitness value of the chromosomes in the population are chosen as the stop criteria of the quantum genetic algorithm in this paper.

• 5)    Update of the population

The crossover and mutation operators are used to maintain the diversity of the population in conventional genetic algorithm. For the quantum genetic algorithm, the rotation of the quantum bits is used to update the chromosomes and maintain the good characteristics of chromosomes in the population. Therefore, the update of quantum bits is important to performance of quantum genetic algorithm. The rotation of the quantum logic bits is used to accomplish the update of population here. The quantum bit rotation is defined as a’ A (cos 6i ji2 J ^ sin Qi

- sin Q ][ a_n cos Q i Jk j ₂

where θ _i = s ( α _{i 1}, β _{i 2}) Δ θ , θ _i is the angle of quantum rotation. The rotation angle should be set appropriately. Large rotation angle may lead to the precocity of genetic algorithm, whereas small rotation angle may slow the evolution speed of genetic algorithm. Table I shows the selection of rotation angle in this paper.

TABLE I.

T HE ROTATION ANGLE OF QUANTUM GENETIC ALGORITHM

xi bi f(x)>f(b) Δθ s(αi1,βi2) αi1βi2> 0 αi1βi2< 0 αi1=0 else 0 0 * * 0 0 0 0 1 1 * * 0 0 0 0 0 1 1 Δθ -1 +1 0 ±1 0 1 0 Δθ +1 -1 ±1 0 1 0 1 Δθ +1 -1 ±1 0 1 0 0 Δθ -1 +1 0 ±1 where f(x) is the target function, which is defined as the fitness function (3) in this paper; s(αi1,βi2) is the symbol function of rotation angle; Δθ is the constant rotation angle. * is the symbol that indicates arbitrary conditions. The detail flow chart of the quantum genetic spectrum assignment model is listed as figure.3.

Figure 3. Flow chart of the quantum genetic spectrum assignment model

• V.    N UMERICAL R ESULTS

  The performance of the proposed genetic spectrum assignment model in this paper is shown. Assuming P primary users are fixed uniformly within an area of 1000 by 1000m, and P available licensed channels are randomly occupied by primary users respectively. The secondary users are randomly distributed within the same

area. The channel availability matrix L and interference matrix C are calculated according to locations of the primary users and secondary users. Here the values of channel reward matrix are normalized as 1, and it can be calculated according to the different requirements of the communication system, such as the maximum bandwidth or throughput.

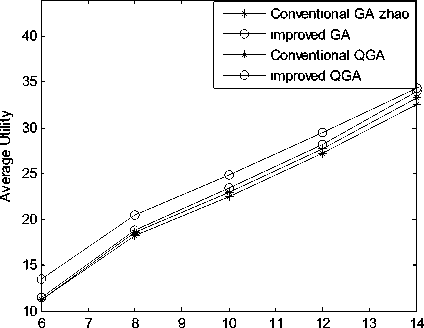
Fig.4 shows the performance of proposed genetic spectrum assignment algorithm with increased number of cognitive users, and it is applied both in the conventional genetic spectrum assignment model and the quantum genetic algorithm model, P =4, the size of the population in different genetic algorithm l p =10, and the length of the chromosome in the population is calculated according the number of the non-zeros elements in the randomly generated channel availability matrix L . In the conventional genetic spectrum assignment model, the crossover probability and mutation probability p c =0.5, p m =0.5 respectively. The constant rotation angle for the quantum genetic spectrum assignment model Δ θ = 0.05 π . The penalty factor for the improved genetic spectrum assignment model σ = 5 , and the constraints-free procedure is performed compulsively to half of the chromosomes in the population for the improved genetic spectrum assignment model. Fig.5 shows the simulation results of the utility performance with various available licensed channels for different genetic algorithms based spectrum assignment model in cognitive radio networks, and the parameters are the same as the ones in fig.4.

It can be concluded from fig.4 and fig.5 that the improved genetic spectrum assignment model proposed in this paper with the consideration of interference constraints of cognitive radio networks can achieve better system utility compared with the conventional genetic spectrum assignment model, and it is the same with the quantum genetic algorithm. In the conventional genetic spectrum assignment model and quantum genetic spectrum assignment model, the constraints-free procedure has to be performed to guarantee the feasibility of the spectrum assignment strategies that corresponds to chromosomes in the population, and it will also cause reduction of the diversity of chromosomes. Thus searching capability of the conventional genetic operator degenerates as the random evolution can’t be realized due to the constraints-free procedure after the crossover and mutation operators. As the quantum bits in the quantum genetic algorithm rotate toward the best solution, the reduction of the fitness value of the chromosomes is mitigated to some extent, but in order to guarantee the feasibility of the chromosomes that achieved by the random observation of the quantum bits in the population, the constraints-free procedure can’t be neglected. In this paper, due to the division of population in genetic algorithm and the quantum genetic algorithm, the randomness of partial chromosomes is reserved, thus searching capability of the population in genetic algorithm and quantum genetic algorithm are improved to some extent. As the extra penalty function is added to the fitness function, the chromosomes that can’t satisfy the interference constraints of assignment model will be eliminated from the population gradually through the evolution of genetic algorithm. The proposed genetic spectrum assignment model can achieve better utility performance for genetic spectrum assignment model and quantum genetic spectrum assignment model.

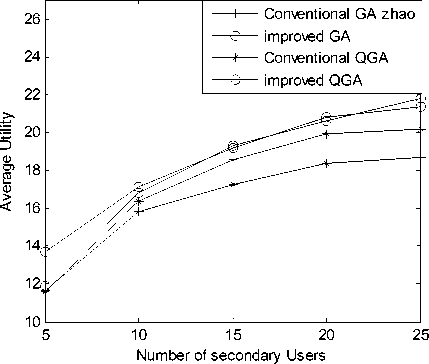
Figure 4. The performance of proposed genetic spectrum assignment models under different cognitive users

Number of available channels

Figure 5. The performance of the proposed genetic spectrum assignment models under different available channels

• VI.    C ONCLUSION

The interference constraints of the genetic algorithm based spectrum assignment model in cognitive radio networks are analyzed, and an improved genetic spectrum assignment model is proposed. The population of genetic algorithm is composed of feasible spectrum assignment and randomly updated spectrum assignment. Constraints-free procedure is performed to part of the chromosomes in updated population, and thus the ratio of feasible solutions among the population is maintained. The penalty function is used eliminate the chromosomes that dissatisfied interference constraints. Due to reserved ratio of feasible solutions, the spectrum assignment strategy with high fitness value can be achieved, and the searching capability for the genetic spectrum assignment model is enhanced. This proposed genetic spectrum assignment model can be applied to both the conventional genetic algorithm and the quantum genetic algorithm, and it can achieve the feasible spectrum assignment strategy and get better system utility performance compared with conventional genetic spectrum assignment model and quantum genetic spectrum assignment model for the cognitive radio networks.

A CKNOWLEDGMENT

The research is supported by the Fundamental Research Funds for the Central Universities (HEUCF100809) and Special Funds for Harbin Technological Innovation and Talents Cultivation Project (2008RFQXG0205).