Генетическая дивергенция в системе смежных популяций при плотностно-зависимом лимитировании гаметопродукции

Институт комплексного анализа региональных проблем ДВО РАН, ул. Шолом-Алейхема 4, г. Биробиджан, 679016, e-mail: , e-mail: ,

Изучение условий, приводящих к формированию и поддержанию существенных генетических различий или первичной генетической дивергенции между несколькими пространственно обособленными популяциями, является сложной междисциплинарной задачей с давней и богатой историей [15, 19]. Для реальных популяций, для которых отмечают дивергенцию, как правило, пытаются найти связь между географической изменчивостью, проявляющуюся в значимых филогенетических различиях на разных участках, и степенью действия какого-либо природного фактора [8, 22, 23]. Кроме того, примеры дивергентных популяций известны именно потому, что такая связь достоверно обнаружена.

Вместе с тем теоретические исследования математических моделей этого явления показывают, что дивергенция может быть связана со свойствами самой популяционной системы, а внешние факторы лишь направляют ее развитие в одно из возможных состояний предельной генетической структуры [11, 27]. В одних состояниях никаких различий между популяциями нет, а в других генетические различия формируются в узком диапазоне начальных условий и при достаточно специфичных ограничениях, накладываемых на рост популяции. Например, показано, что для достижения дивергенции между разными популяциями недостаточно только лишь генетических механизмов – необходим еще сильный экологический механизм, обеспечивающий регулирование роста численности, который должен существенно влиять на эволюционные процессы [9, 11, 13]. Ранее нами показано, что генетическая дивергенция возникает и сохраняется, если соотношение численностей ограничено и не меняется во времени [5]. В других работах показано, что генетические и экологические процессы должны действовать с сопоставимыми скоростями [14, 21]. Ограничения роста могут быть связаны с разнообразными механизмами самолимитирования внутри популяции [12, 20, 27] или межвидовыми взаимодействиями [16, 24, 25].

Поэтому возникает задача исследования механизмов, приводящих к генетической дивергенции в системе связанных популяций с лимитированием роста численности, из которой максимально исключено влияние гетерогенности условий существования. В частности, в условиях одинаковости действия отбора во всех популяциях. Также важно понять, при каких условиях генетическая дивергенция будет устойчивой и сохранится при нарушении пространственной изоляции между популяциями.

Настоящая работа продолжает начатое в [5, 10, 11] изучение механизмов и условий возникновения первичной генетической дивергенции. Предложена математическая модель с дискретным временем, основанная на рекуррентных уравнениях (отображениях) и описывающая изменение частот аллелей и динамику численности в системе двух миграционно связанных панмиктичных популяций с монолокусным отбором. Рассматривается случай, когда в двух смежных популяциях действует диз-руптивный (разрывающий) отбор, проявляющийся в пониженной приспособленности гетерозигот по единственному диаллельному локусу. Кроме того, изучаются изменения режимов динамики численностей, происходящие при достижении популяциями однородного по ареалу генетического состава, когда популяции мономорфны по рассматриваемому локусу, или неоднородного состава, когда популяции полиморфны и существенно отличаются концентрациями генотипов.

Модельные уравнения системы неограниченно растущих популяций Рассмотрим модельную систему двух популяций с непересекающимися поколениями, связанных миграцией со следующими ограничениями [11].

Особи внутри каждой из популяций имеют генетические различия, которые проявляются в разной скорости воспроизводства и приспособленности. При образовании зигот из гамет в процессе воспроизводства наблюдается локальная панмиксия, т.е. происходит свободное и случайное слияние гамет независимо от их генотипа и того, кто их произвел. В простейшем случае к отбору чувствителен единственный диаллельный локус, представленный аллеломорфами A и a . Отбор осуществляется на диаллельной стадии, т.е. отбираются только зиготы. Предположим, что мигрируют только взрослые особи (зиготы). В этом случае будем предполагать, что существует следующая элементарная последовательность популяционных процессов: формирование зигот из гамет, отбор зигот, миграция зигот между популяциями, продуцирование новых гамет и т.д. Миграция при этом может происходить непосредственно после отбора либо предшествовать отбору.

В общем случае, когда популяции неидентичные, каждый перечисленный элементарный популяционный процесс характеризуется следующими коэффициентами:

– gAA, gAa, gaa, hAA, hAa и haa – гаметопродук- ция первой (gij) и второй (hij) популяций, равная среднему числу гамет, производимому одной особью с генотипами AA, Aa и aa. В эти коэффициенты неявно входит отбор гамет с учетом того, что большая часть гамет гибнет еще до процесса оплодотворения. Коэффициенты gij и hij способны принимать любые неотрицательные значения.

– W_AA , W_Aa , W_aa , V_AA , V_Aa и V_aa – приспособленность зигот с генотипами AA , Aa и aa первой ( W_ij ) и второй ( V_ij ) популяций, равная доле зигот (взрослых особей), которые приступят к миграции на следующем этапе. Приспособленности принимают любое значение от 0 до 1.

– m – коэффициент связи или миграции, который принимается равным для каждой популяции и генотипа (симметричная миграция). Он принимает любое значение от 0 до 1.

Для описания динамики описанной системы популяции удобно следить не за абсолютными численностями гамет, а за долей (концентрацией) гамет, несущих, например, аллель A к общему числу гамет всех типов. Обозначим это число для первой и второй популяций через q ₁ и q ₂. Тогда доля гамет с аллелем a для обеих популяций равна 1– q ₁ и 1– q ₂ соответственно.

В этом случае динамика рассматриваемой системы популяций в общем случае описывается системой из шести уравнений, характеризующих изменение концентрации q ₁ и q ₂, общего числа гамет всех типов, а также общей численности N ₁ и N ₂ первой и второй популяций. Не будем приводить здесь ее общий вид, поскольку это потребует описания ряда дополнительных переменных. Для уменьшения числа динамических переменных необходимы дополнительные допущения. Например, можно положить, что популяции не отличаются по приспособленностям зигот разных типов или гаметопродукции или, дополнительно, что гаметопродукция не зависит от генотипов производящих их особей.

В самом предельном случае, когда популяции идентичны, а генотипы отличаются лишь приспособленностями, удается перейти к трем относительно негромоздким уравнениям. Для этого помимо фазовой переменной q1 и q2, вводится относительная величина p=N1/(N1+N2), равная весу первой популяции к общей численности всей системы популяций. Однако при этом теряется информация о некоторых режимах динамики численностей N1 и N2. В частности, независимо от того, неограниченно или ограниченно будут расти численности, вес p всегда будет ограничен. Например, при синхронном росте независимо от характера динамики численности вес будет стремиться к 1/2, а при несинхронном росте к значению из интервала (0;1). Подробный вывод уравнений можно найти в монографии [11], а подробное исследование модели в статьях [5, 10].

Рассмотрим немного более общий случай, когда две популяции имеют разные приспособленности и гаметопродукцию. Будем полагать, что гаметопродукция не зависит от генотипов производящих их особей, но все же отличается для разных территорий, т.е. gAA=gAa=gaa=g и hAA=hAa=haa=h. В этом случае оказывается, что общее число гамет каждой популяции прямо пропорционально численности с коэффициентом пропорциональности g и h. Поэтому в модельные уравнения можно включить лишь одну из этих величин (численность или число гамет). В этом случае оказывается, что коэффициенты g и h равны среднему числу новорожденных, производимых одной особью до процесса отбора и миграции. Тогда для популяций с непересекающимися поколениями и дискретным временем можно получить следующую систему динамических уравнений:

q i ^{( t} + 1 ) =I^{( 1} - m ^{)( w}a A q 1 ⁽ t ) + W Aa q ^{1 (} t X¹ - q ^{( t )) ) +} G i ⁽ t ) i

⁺ mNHT) ( V A A q 2 ^{( t )+ v}a a q ^{2 ( t} )( 1 - q 2 ⁽ t ^l N 1 ( t )                                    ;

■ q 2 ^{( t +} 1 ) =^{1 1} - m^jq^{2 (} t ⁾⁺ V Aa q 2 ⁽ t X¹ - q 2 ⁽ t ^{)) ) +} (1) G 2 ( t ) i

⁺ m N f ⁽ W a A q ^{2 ( t} ) ⁺ W Aa q 1 ^{( t} )( 1 - q 1 ⁽ t^

N 1 ( t + 1 ) = ( 1 - m ) gw 1 N 1 ( t ) + m hw 2 N 2 ( t ),

N2(t +1)= (1 - m)hw2N2(t)+ m gw1 N 1 (t), где множители w1 (t ) = WA Aq\ (t)+ 2Wa aq1 (t )(1 - q1 (t)) +

^{+ W}a a ^{( 1 -} q 1 ⁽ t ^{)) 2} и w 2 ⁽ t ) = V A A q 2 ^{( t} ) ⁺ 2V A a q 2 ⁽ t ^{)( 1 -} q 2 ^{( t )) +}

+ Vaa (1 - q 2 (t ))2 показывают обобщенную приспособленность первой и второй популяций до процесса миграции, а мно- жители       G1 (t) = (1 - m)W1 (t)+m N2 (t) w2 (t)

и

G2 (t)= (1 - m)w2 (t)+m N 1 (tt) w1 (t) равны обобщенной приспособленности после миграции и показывают, во сколько раз увеличилось (уменьшилось) за одно поколение число особей. В этом случае из-за различного действия отбора в смежных популяциях (Wij ≠ Vij) не удается перейти от двух уравнений динамики численностей к одному уравнению динамики веса p первой популяции.

Модель с учетом плотностно-зависимого лимитирования

Рассмотрим действие плотностно-зависимого лимитирования в рассматриваемой системе популяций с принятыми допущениями о независимости гаметопродукции от генотипов производящих их особей.

Несмотря на то, что в системе (1) из-за миграции частоты аллелей зависят от соотношения численностей N ₁/ N ₂ ( N ₂/ N ₁), нет оснований говорить о существенной зависимости отбора от численностей. В данном случае из-за постоянного движения особей в смежных популяциях могут поддерживаться разные распределения частот аллелей, которые в целом характерны для одиночной популяции без миграции (при m= 0). В результате в системе (1) при m >0 появляются довольно простые бассейны притяжения мономорфных и полимофных состояний. Вид этих бассейнов зависит не от конкретных значений численностей, а от предельного значения соотношения N ₁/ N ₂. На тип динамики частот аллелей миграционная связь не оказывает существенного влияния [5].

В системе (1) действие плотностно-зависимых факторов, лимитирующих рост численности, может быть описано через зависимость параметров отбора W_ij и V_ij или гаметопродукции g и h от численностей N ₁ и N ₂ (плотности населения). В первом случае изменятся сразу все модельные уравнения. Первые два уравнения будут содержать явную зависимость отбора от численностей. Во втором случае изменятся только лишь уравнения динамики численностей, и отбор останется относительно независимым от плотности (с учетом зависимости от N ₁/ N ₂).

По всей видимости, именно последний вариант достаточно распространен, поскольку часто природная генетическая изменчивость по признакам, по которым идет отбор, слабо коррелирует c изменениями плотности в популяции [17, 18]. Этому есть множество объяснений, суть которых сводится к тому, что экологические и генетические процессы в таких популяциях идут в разных временных шкалах [14, 21].

Поэтому рассмотрим именно последний вариант.

Из уравнений (1) ясно, что число новорожденных особей равно gN ₁ и hN ₂, а число особей после отбора, т.е. с учетом смертности, g w ₁ N ₁ и h w ₂ N ₂ . Положим, что рождаемость первой и второй популяций можно описать убывающими функциями вида:

g = g 1^{F (} N 1 ) и h = g 2 F ⁽ N 2 ) ,        ⁽²⁾

где F(N) – убывающая функция (F(0)=1 и Fʹ(N)<0), характеризующая плотностную регуляцию чис- ленности, одинаковую для каждого генотипа. Параметр g1 и g2 – максимально возможное число новорожденных, производимое одной особью (рождаемость) в первой и второй популяциях при минимальной численности. Темп убывания функции F зависит от ее конкретного вида. Например, если функция выбрана по аналогии с уравнением Ферхюльста, т.е. F(N)=1–N/K, то рождаемость линейно падает до величины K, равной максимально возможной численности и называемой экологиче- ской нишей, а при N>K модель теряет смысл. Если функция F выбрана по аналогии с моделью Рикера: F(N)=exp(–N/K), то рождаемость медленно па- дает для небольших N и быстро для больших N.

С учетом (2) система (1) приобретает вид:

q 1 ^{( t} +0=—7-I ^{( 1 -} mW A q ! ^{( t} )+ W Aa q 1 ^{( t )( 1 -} q 1 ^{( t )))+}

" 1 ⁽ t ) V

^

+ m^JA (VA Aq2 (t)+ VA aq2 (t)(1 - q2 (t)))l, N1(t)J q 2(t+1)=G^(t) I(1 - m )(va Aq 2(t)+VAaq 2(t X1 - q 2(t)))+

2 л т(Л,

⁺ m        ^{( w} a A q ^{2 (} t ^{)+ w} a a q 1 ^{( t )( 1 -} q 1 ⁽ t ⁾⁾⁾ l ^,

N 2 (t)

N 1 ^{( t} + ^{1 )} = ^{( 1 -} m ) g 1 w 1 N 1 ⁽ t ) F ⁽ N 1 ^{( t ))+} m g 2 w 2 N 2 ⁽ t ) F ⁽ N 2 ^{( t} )) ,

_ N 2 ⁽ t + Hi! - m ) g 2 w 2 N 2 ⁽ t ) F ⁽ N 2 ⁽ t )) + mg 1 W 1 N 1 ⁽ t ) F ⁽ N 1 ⁽ t ))■

Для дальнейшего исследования модели (3) выберем такой тип отбора, который способен привести к возможности установления устойчивых различий или дивергенции в обеих популяциях, особенно в условиях одинаковости действия отбора на разных участках. Здесь возникает соблазн положить равными приспособленности для одних и тех же генотипов на смежных участках. Однако, по всей видимости, достаточно, чтобы совпадал лишь характер действия отбора, т.е. соотношение приспособленностей оставалось одинаковым для обеих популяций. Несложно понять, что единственный тип отбора, который может привести к дивергенции, – дизруптивный отбор. В рассматриваемой модельной ситуации монолокусного отбора это соответствует пониженной приспособленности гетерозигот, при которой приспособленность гетерозигот не превосходит приспособленности гомозогот, т.е. W_Aa < W_AA , W_Aa < W_aa и V_Aa < V_AA , V_Aa < V_aa . Поскольку здесь важны именно соотношения параметров, можно ограничиться «симметричным» случаем:

w _aa = w _qq =v _aa = v _qq = 1 и W_Aa= 1 - 5 1 , v_Aa= ¹ - 5 2 где 0 <  s i < 1 - интенсивность отбора гетерозигот.

В этом случае система (3) упрощается и имеет вид:

q i ⁽ t + 1 ) =

Г(1 - m q (t)(1 - S i(1 - qi(t)))+ )

G 1 ⁽ t ) + m V

q 2 (t)(1 - S 2 (1 - q 2 (t))) ’ x 1(t)                           J

r ^{( 1} - m ) q 2 ⁽ t ^{)( 1} - ^S 2 ^{( 1} - q 2 ^{( t} Ж - '

, q 2 ( t + 1 ) =

g 2 ( t ) ⁺ m x^ q 1 ⁽ t ^{)( 1} - ^S 1 ^{( 1} - q ⁽ t ))) ’ V      x 2 ^{( t} )                         J

^{( t +} 1 ) = ^{( 1 -} m ) g 1 w 1 ^x 1 ⁽ t ) ^{F ( x} 1 ⁽ t )) ⁺

x ₁

+ mg 2 w 2 x 2 ⁽ t ) F ⁽ x 2 ⁽ t )), ^x 2 ^{( t} + 1 ) = ( 1 ^- m ) g 2 w 2 x 2 ^{( t} ) F ⁽ x 2 ^{( t} )) +

+ mg 1 w1 x 1 (t)F (x 1 (t)), где w1 - 1 - 2S1Q1(t)(1 - Q1(t)) , w2 - 1 - 2q2 (t)(1 - q2 (t)) ,

G 1 - ( 1 - m ) w 1 + m-N-w ₂ и G ₂ - ( 1 - m ) w ₂ + mN-w 1 ;

x_i = N_i / K_i – относительная численность ( i =1,2), перейти к которой возможно для многих убывающих функций F , в том числе F ( N i ) - 1 - N i I K i и F ( N ) - exp ( - N I K ) .

Последние два уравнения системы (4) – это система двух симметрично связанных неидентичных логистических отображений с переменными коэффициентами w _i ( i =1,2). Поэтому следует ожидать наследования части свойств динамики, характерных для связанных отображений, в частности свойств, связанных с синхронизацией колебаний численностей x ₁ и x ₂, а также фазовой мультистабильностью. Эти явления хорошо изучены как для идентичных [1, 3, 4, 6], так и для неидентичных отображений [2, 7], чем в общем случае и является система (4). По мере того как генетическая структура стремится к какому-либо состоянию (мономорфизм или полиморфизм), происходит изменение значений концентраций q ₁ и q ₂, которое меняет значение параметров w ₁ и w ₂ , и, как следствие, изменяется характер динамики численностей. Поэтому следует ожидать разнообразных нелинейных эффектов именно в переходной динамике, когда меняется генетическая структура. Достигнув же финитного распределения частот генотипов, характер динамики системы будет определяться именно последними двумя уравнениями, которые в свою очередь могут, при определенных условиях, изменять предельное состояние генетической структуры (через множитель x ₁/ x ₂). В частности, колебания численностей x ₁ и x ₂ могут провоцировать колебания концентраций q ₁ и q ₂.

Вычисление состояний равновесия

Рассмотрим состояния устойчивости (неподвижные точки) системы (4), а также обсудим условия их существования и устойчивости.

Неподвижные точки системы (4) удовлетворяют следующей системе уравнений:

q 1 = -L | ( 1 - m ) q 1 ( 1 - S 1 ( 1 - q 1 )) + mq 2 ( 1 - S 2 ( 1 - q 2 )) | =

G1 v                            x 1

= Q 1 ⁽ q 1 , q 2 , x 1 , x 2 ),

(1 - m)q 2(1 -S 2(1 - q 2))+mXL q 1(1 -S1(1 - q1 ))|= (5) x 2

q 2 = тг I

G ₂

= Q 2 (q 1, q 2 x 1^_x 2 ),_

• ^x 1 = ^{( 1} - ^m ) g 1 ^w 1 ^x 1 ^{F ( x} 1 ) ⁺ mg 2 ^w 2 ^x 2 ^{F ( x} 2 ) = ^Ф 1 ⁽ q 1 , q 2 , ^x 1 , ^x 2 ),

„ x 2 = ⁽ 1 - m ) g 2 w 2 x 2 F ⁽ x 2 ) + m g 1 w 1 x 1 F ⁽ x 1 ) = Ф 2 ⁽ q 1 , q 2 , x 1 , x 2 ), которую крайне сложно решить в общем виде, даже выбрав конкретный вид функции F . Однако несложно указать несколько очевидных ее решений (неподвижных точек), соответствующих однородной генетической структуре в обеих популяциях:

• 1)    E 0 ( 0,0 ,x 1 ,x 2 ) - обе популяции представлены только особями с генотипом аа (отсутствуют генотипы АА или Аа ) (мономорфные популяции);

• 2)    E 1 ( 1I2,1I2 ,x 1 ,x ₂ ) - обе популяции включают особей всех генотипов с одинаковой концентрацией гомологичных аллелей (полиморфные популяции);

• 3)    E ₂ ( 1,1 ,x 1 ,x 2 ) - обе популяции состоят только из особей с генотипом АА (мономорфные популяции).

Подставив эти координаты в систему (5), несложно найти конкретные значения x ₁ и x ₂ . Для точек E ₀ и E ₂ из системы уравнений вида:

x 1 =(1 - m)g 1x 1F (x 1)+mg 2x 2F (x 2), x 2 = (1 - m)g 2 x 2 F (x 2)+ mg 1 x 1 F (x 1).

Для точки E ₁ из системы вида:

j 2 x 1 = ⁽ 1 ^- m ⁾⁽ 1 ^- s 1 ) g 1 x 1 F ⁽ x 1 ⁾⁺ m ⁽ 1 ^- s 2 ) g 2 x 2 F ⁽ x 2 ), [ 2 x 2 = ( 1 - m )( 1 - s 2 ) g 2 x 2 F ( x 2 ) + m ( 1 - S 1 ) g 1 x 1 F ( x 1 ).

Обе этих системы уравнений разрешимы в конечных функциях лишь для некоторого класса рациональных функций F, например, для F(x)=1–x. В остальных случаях необходимо использовать приближенные методы. Можно строго доказать, что для любой убывающей функции F при допустимых значениях параметров каждая из этих систем имеет тривиальное и несколько нетривиальных решений, одно из которых всегда ле- жит в первом квадранте плоскости (x1,x2). Однако тривиальное решение x1=x2=0 следует исключить из возможных решений, поскольку оно приводит к неопределенности 0/0 в системе (4).

Для определения неподвижных точек, соответствующих неоднородной генетический структуре, или, другими словами, генетической дивергенции, обратим внимание, что первые два уравнения системы (5) не зависят от выбора функции F . Более того, можно показать, что переменные x ₁ и x ₂ могут быть «исключены» из первых двух уравнений системы (5). В этом случае поиск неподвижных точек сведется к поиску таких значений q ₁ и q ₂, которые удовлетворяют первым двум уравнениям, а затем исключению той части из них, которые не удовлетворяют третьему и четвертому уравнению системы (5).

Действительно, домножив обе части первого и второго уравнения системы (5) на G ₁ и G ₂, можно получить систему алгебраических уравнений вида:

(1 - m ) A 1 x 1 + m B 1 x 2 = 0,

(1 - m) A2 x2 + m B2 x 1 = 0, где Ai =$q (1- qi X1- 2 qi), A2 = s2q 2 (1- q 2 )(1- 2 q 2 ) Bi = qi- q 2 +s2q 2(1 - q 2)(1 - 2 qi) и Bi = qi- q 2+ + s1q1 (1 - q1 )(1 - 2q2). Учитывая, что x 1 * 0 и x2 * 0 по условию, выразим x1 из первого уравнения и подставим результат во второе и разделим на x2 * 0 . В результате получим полином двух переменных q1 и q2:

P ( q i q ) = ( 1 - m ) ² A i A 2 - m ² B i B 2 , нули которого содержат все корни для первых двух уравнений системы (4) при любых фиксированных x 1 * 0 и x ₂ * 0 , в том числе E 0 , E 1 и E ₂. Остается лишь выбрать из них те, которые удовлетворяют последним двум уравнениям системы (5).

Поиск нулей полинома P выполним методом сканирования. Для этого будем перебирать значения, например, q1 в некотором допустимом диапазоне значений. Зафиксировав q1 = q1 , будем искать значения q2 = q2, для которых P(q1 ,q2) = 0. Этот полином имеет степень 3 относительно переменной q2, и поэтому содержит 1 или 3 действительных корня, которые можно найти, например, по формуле Кардано. В результате на плоскости (q1,q2) можно изобразить несколько кривых, точки которой являются нулями полинома P(q1,q2). В полном фазовом пространстве они образуют ги- перцилиндрическую поверхность, на которой лежат все неподвижные точки системы (3). В левом столбце на рис. 1 показано, как выглядят эти кривые при конкретных значениях параметров.

Далее среди нулей полинома P необходимо найти такие значения, которые являются решением системы (5). Для этого каждый из нулей q 1 ^* и q 2 подставим в третье и четвертое уравнение системы (4), т.е. будем решать систему двух уравнений:

= x _i -

АФ 1

АФ 2

Ф 1 ⁽ q * , q \, x i , x 2 ) =0, Ф 2 ( q * , q \, x i , x 2 ) = 0.

= x ₂ -

Как уже отмечалась, система вида (6) для убывающих функций F имеет не менее одного нетривиального решения. Его можно найти явно из аналитически полученной формулы или численно, что зависит от выбора вида функции F . В результате каждой точке ( q 1 ,q₂ ) ставится в соответствие одна (или несколько) точек ( x 1 ,x₂ ) , удовлетворяющих системе (6). В плоскости ( x ₁, x ₂) найденные точки ( x 1 ,x₂ ) образуют несколько кривых подобно тому, как нули полинома P ( q ₁, q ₂) задают гиперцилиндр. Во втором столбце на рис. 1 можно увидеть примеры этих кривых при F ( x )=1– x . Заметим, что определяемое системой (6) отображение плоскости ( q ₁, q ₂) в ( x ₁, x ₂) не является взаимно однозначным. На рис. 1 можно увидеть, что ветви нулей полинома P ( q ₁, q ₂), лежащие на плоскости ( q ₁, q ₂), при q ₁<1/2 и q ₁>1/2 имеют совпадающие образы на плоскости ( x ₁, x ₂), что, по всей видимости, связано с симметричностью функции F ( x )=1– x . В частности, совпадают точки E ₀ и E ₂, которые имеют разные прообразы q ₁= q ₂=0 и q ₁= q ₂=1. В плоскости ( x ₁, x ₂) также совпадают образы искомых неподвижных точек E ₃ и E ₄, соответствующих неоднородной генетический структуре. Это означает, что противоположные предельные состояния генетических структур (много гамет с аллелем A и мало a или наоборот) приводят к одинаковым предельным распределениям численностей.

Среди корней ( x 1 ,x₂ ) системы (6) и поставленных им в соответствие точек ( q 1 ,q₂ ) необходимо оставить лишь те, которые удовлетворяют первым двум уравнениям системы (5), т.е. являются корнями системы вида:

****

I ^А Q i = q i ^- Q i ( q i , q 2 , x i , ^x 2 ) =0, [^А Q 2 = q 2 ^- Q 2 ⁽ q * , q 2 , x * , x 2 ) = 0.

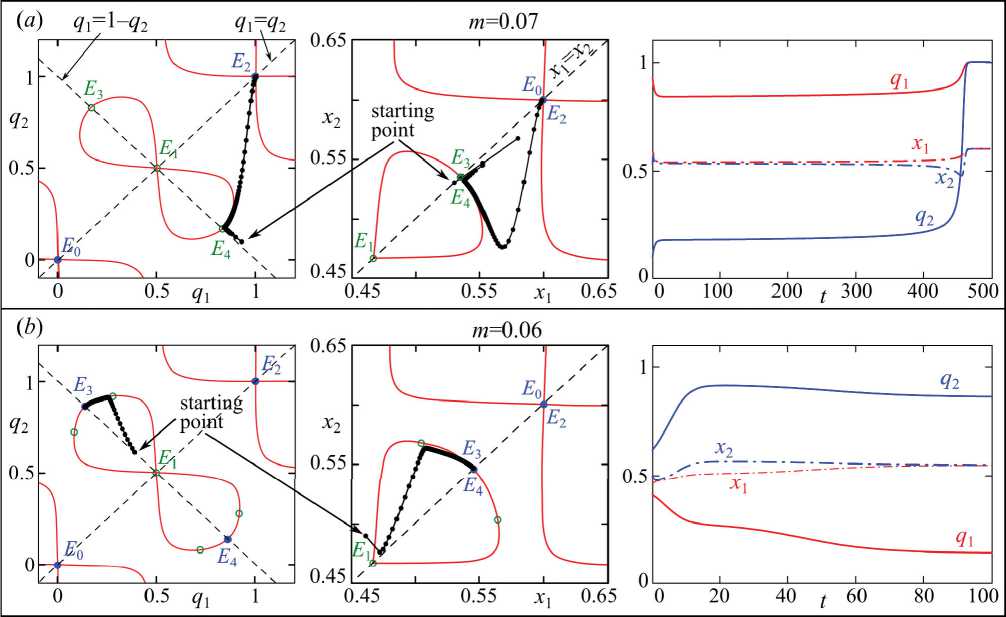
Рис. 1. Слева - фазовые портреты системы (4) при F ( x ) = 1 - x , s 1 =s 2 =0.5 и g 1 =g 2 =2.5. Синий кружок – устойчивая неподвижная точка, зеленый выколотый – неустойчивая точка, черные точки – траектория системы (4) для отмеченной стартовой точки. Красные линии – нули полинома P ( q 1 , q 2 ) в плоскости ( q 1 , q 2 ) (слева) и ( x 1 , x 2 ) (в центре). Справа - динамика частот аллелей и численностей в смежных популяциях

Fig. 1. On the left - phase portraits of the system (4) at F ( x ) = 1 - x , s 1 =s₂=0.5 and g 1 =g₂=2.5. The blue circle – a stable fixed point, the green circle – an unstable point, the black dots – a trajectory of the system (4) for the marked starting point. On the right – dynamics of allele frequencies and abundances of adjacent populations

С учетом того, что начальное значение q1* выбирается достаточно произвольно и изменяется с некоторым фиксированным шагом, ни одна из найденных на предыдущем шаге точек (q1 ,q2,x1,x2) никогда не будет удовлетворять системе (7). Вместе с тем можно утверждать, что с точностью до шага сканирования в окрестности некоторых из них будут лежать искомые корни системы (5). Для поиска точек, в окрестности которых лежат корни, воспользуемся известным фактом. Если функции ΔQ1 и ΔQ2 для двух достаточно близких точек меняют свой знак, то между ними лежит корень системы (7). Тогда для поиска корней (7) будем двигаться строго вдоль веток кривой, задаваемой корнями уравнения P(q1,q2)=0. Если для двух соседних ее точек ΔQ1 и ΔQ2 меняют свой знак, то в качестве начального приближения корня системы (5) можно взять их среднеарифметическое значение. В свою очередь эта средняя точка может быть использована как хорошее начальное приближение, гарантирующее быструю сходимость к искомому решению при использовании методов спуска.

На рис. 2 показано, как изменяется разность Δ Q ₁ при движении вдоль разных ветвей кривой P ( q ₁, q ₂)=0 и их образов на плоскость ( x ₁, x ₂). На каждой из этих линий численности x ₁ и x ₂ принимают такие значения, что ΔΦ₁=ΔΦ₁=0. Аналогичным образом изменяется разность Δ Q ₂ в зависимости как от q ₁, так и q ₂. Следовательно, в окрестности точки пересечения Δ Q ₁ с осью абсцисс лежит неподвижная точка. На рис. 2 выделены лишь те из них, которые имеют положительные координаты. Кроме того, эти графики показывают механизм рождения состояний равновесия, соответствую-

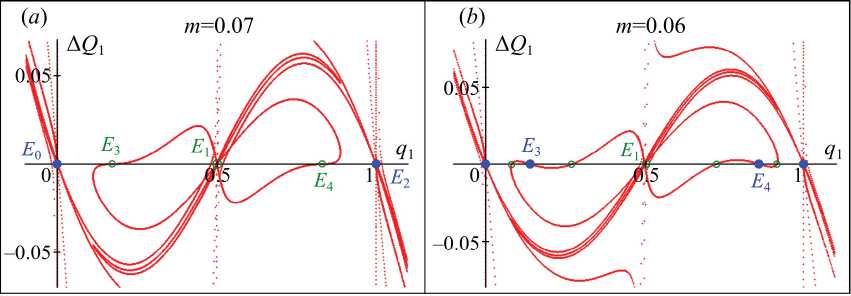
Рис. 2. Графики нулей полинома P ( q 1 , q 2 ) , для которых верно А Ф 1 = А Ф 2 = 0 .

Точки пересечения с абсцисс – неподвижные точки, среди которых кружками выделены имеющие неотрицательные координаты

Fig. 2. Graphs of the polynomial zeros P ( q 1 , q 2 ) for which А Ф 1 = А Ф 2 = 0 is true.

The points of intersection with the abscissa are fixed points, among which there are the circles marked with non-negative coordinates щих генетической дивергенции, а также позволяют косвенно оценить устойчивость неподвижных точек.

Рассмотрим, как формируются и когда устойчивы найденные неподвижные точки, и какие режимы динамики при этом возникают.

Сценарии потери устойчивости

При достаточно низкой интенсивности отбора гетерозигот s1 и s2 или достаточно больших значениях параметра миграции m система (4) содержит неустойчивую неподвижную точку E1 и две устойчивые точки E0 и E2. График разности ΔQ1 при этом состоит из одной-единственной линии, которая пересекает ось абсцисс в точках E0, E1 и E2. Динамика системы (4) при этом оказывается бистабильной: при q(0)<1–q2(0) траектория стремится к точке E0, при q(0)>1–q2(0) к точке E2. С ростом s1 и s2 или уменьшением m от точки E1 отщепляется пара седловых точек E3 и E4, которые лежат на границе бассейнов притяжения точек E0 и E2 (q(0)=1–q2(0)). Две этих точки соответствуют генетической дивергенции между двумя миграци-онно связанными популяциями. При некоторых начальных условиях модельная траектория может достаточно близко приблизиться к одной из этих точек. В результате в переходной динамике системы (4) будут зафиксированы продолжительные участки, в которые две популяции имеют существенные генетические различия как по частоте генотипов, так и численностям (особенно если отличаются значения s1, s2, g1 и g2). Однако выйдя из окрестности седловой точки E3 или E4, траектория быстро устремится к одному из мономорфных состояний E0 или E2 и популяции окажутся идентичными. Пример такой динамики показан на рис. 1a.

По мере роста интенсивности отбора или снижения коэффициента миграции точки E3 и E4 отдаляются от E1, в их окрестности рождается дополнительная пара точек, и точки E3 и E4 приобретают устойчивость. Этот сценарий существенно отличается для идентичных и неидентичных популяций. В случае s1=s2 и g1=g2 пара новых точек симметрична относительно E3 или E4 и лежит по обе стороны от них (рис. 1a). Результат такого мягкого расщепления (бифуркации вил) точек E3 и E4 показан на рис. 1b. Любое нарушение равенства параметров отбора или рождаемости нарушает эту симметрию, и новая пара рождается в ходе седло-узловой бифуркации. По мере роста отличий популяций по рождаемостям g1 и g2 неподвижные точки и нули полинома P(q1,q2) в плоскости (x1,x2) отдаляются от линии x1=x2 (на которой лежат полностью синхронные режимы динамики) и смещаются в сторону более высоких значений численностей той популяции, у которой выше рождаемость. Вместе с тем график P(q1,q2)=0 в плоскости (q1,q2) не меняет своего вида, однако изменение стационарных значений численностей смещает неподвижные точки E3 и E4 вдоль этой кривой, а также пар точек, окружающих их. Рост различий популяций по интенсивности отбора s1 и s2 меняет вид графика P(q1,q2)=0 как в плоскости (q1,q2), так и (x1,x2). Но более важно, что любое отличие между популяциями меняет механизм формирования неподвижных точек, соответствующих устойчивой генетической дивергенции. В этом случае в стороне от седловых точек E3 и E4 рождается пара из устойчивой и неустойчивой точек (узел и седло). Чтобы не вводить новых обозначений, будем далее обозначать эти устойчивые точки как E3 и E4.

После рождения устойчивых точек E ₃ и E ₄ динамика системы (4) оказывается квадроста-бильной. В этом случае в зависимости от начальных условий популяции могут перейти к одному из четырех состояний, отличающихся частотами генотипов и предельными численностями: два варианта однородных мономорфных по генотипам популяций с нулевой частотой аллеля a или A , одинаковой на смежных участках, и два варианта полиморфных популяций с разной концентрацией гомологичных аллелей. В случае мономорфизма популяции имеют более высокую численность, чем в случае полиморфизма. Причем чем сильнее популяции различаются в частотах аллелей, тем больше разница численностей для мономорфной и полиморфной популяций будет наблюдаться. По всей видимости, по этой причине точки E ₃ и E ₄ теряют устойчивость при более высокой рождаемости, чем мономорфные точки.

Как уже отмечалось, система (4) наследует часть свойств от системы связанных логистических отображений, связанных с механизмами потери устойчивости неподвижных точек и синхронизации динамики. С ростом репродуктивного потенциала, аналогом которого в системе (4) является множитель g_iw_i , для систем связанных отображений характерен следующий сценарий потери устойчивости. По мере роста репродуктивного потенциала один из мультипликаторов переходит через –1 (остальные по модулю меньше 1) и из нетривиальной неподвижной точки рождается синфазный 2-цикл. Дальнейшая его эволюция связана с каскадом удвоения периода. Вместе с тем по мере снижения коэффициента миграции m неподвижная точка второй раз испытывает удвоение периода, когда второй мультипликатор переходит через –1. Однако дополнительный 2-цикл может быть лишь противофазным. Дальнейшее его усложнение связано со сложной цепочкой формирования предельных инвариантных кривых и появлением разнообразных, часто сосуществующих резонансных циклов, которые отличаются фазами и периодами колебаний x ₁ и x ₂. В результате при больших значениях репродуктивного потенциала и малой миграции m динамика численностей x ₁ и x ₂ оказывается мультистабильной.

Вместе с тем в полной системе (4) значение параметра g_iw_i зависит от частот генотипов q ₁ и q ₂. В результате разным видам предельной генетической структуры соответствуют разные значения аналога репродуктивного потенциала g_i w _i . Несложно убедиться, что в случае мономорфных популяций репродуктивные возможности, т.е. значения ^giwi , будут выше, чем в случае полиморфных, из-за разницы в приспособленно-стях гомо- и гетерозигот. Поскольку при q_i → 0 или q_i → 1 w _i → 1 , а при ^^^е(о,1) и q ₁ ≠ q ₂ w, 1 - хд (1 - % ) е (0,1) и w ₁ ≠ w ₂ . Как следствие, координаты неподвижных точек, соответствующие двум этим типам генетической структуры, будут различными. Это верно и для полностью идентичных популяций ( s ₁= s ₂= s и g ₁= g ₂= g ). Например, при движении к мономорфизму значения репродуктивных потенциалов всегда сближаются ( g w ₁ → gw ₂ ), а при движении к полиморфизму они всегда будут разными ( g w ₁ ≠ gw ₂ ). В результате вне области устойчивости при одних начальных условиях формируются генетически однородные популяции (мономорфизм), но с выраженными синфазными или противофазными колебаниями численностей, при других возникают генетически неоднородные популяции (полиморфизм) без колебаний численностей.

На рис. 3 показано несколько примеров перехода к такому распределению, где использованы разные рождаемости для смежных популяций. В этом случае стационарные уровни численностей разных популяций будут отличаться ( x ₁ ≠ x ₂ ) как при движении к мономорфному, так и полиморфному состоянию популяций.

В первом примере возможны два режима динамики (рис. 3 a ). Рассмотрим их. Во-первых, обе популяции имеют существенные генетические различия, касающиеся концентрации гомологичных аллелей. Численности популяций устойчивы и стремятся к предельному состоянию, характеризуемому максимальным размером той популяции, у которой выше рождаемость. Во-вторых, популяции в предельном случае генетически однородны и представлены только особями с генотипом AA или аа . В данном примере первая популяция имеет рождаемость ниже бифуркационного значения ( g ₁ w ₁ = 3) и в отсутствие связи (при m =0) не способна генерировать собственные колебания. Поэтому ее колебания при m >0 строго следуют за колебаниями численности второй популяции, но

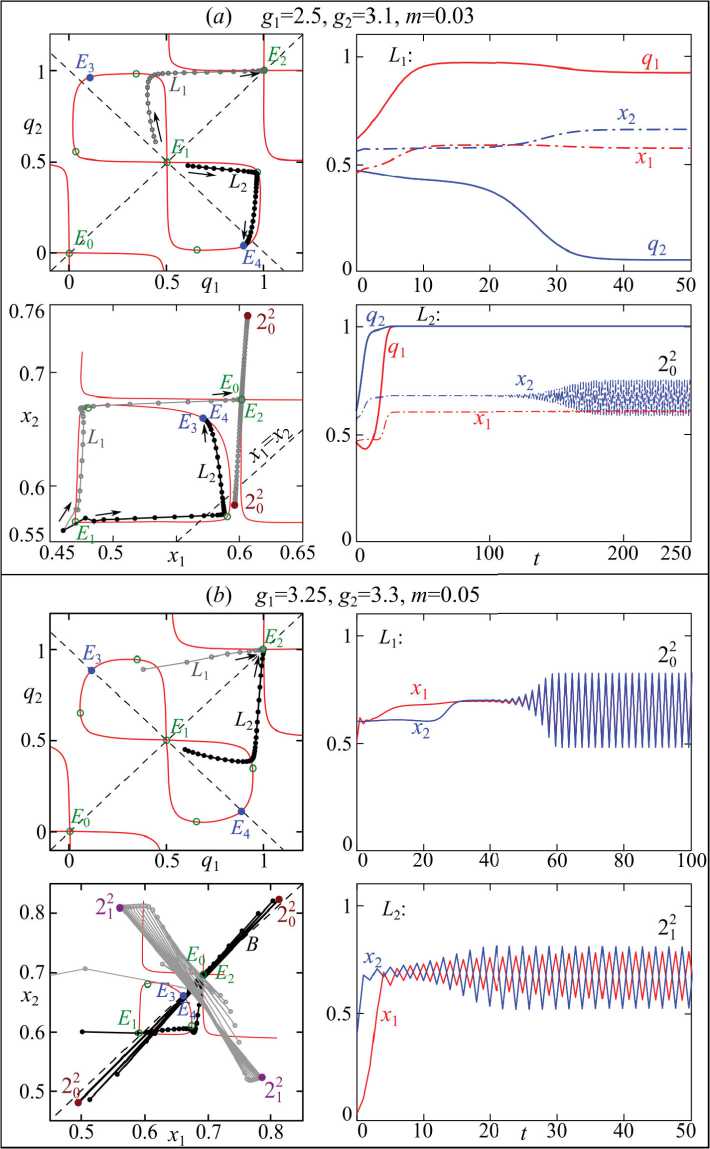
Рис. 3. Первый столбец – фазовые портреты системы (4) при F ( x ) = 1 - x и s₁=s₂=0.5, остальные значения параметров показаны на рисунке. Черные и серые кружки – траектория системы (4) для разных начальных условий, стрелки рядом с ними показывают направление движение траектории. Второй ряд – динамика частот аллелей и численностей в смежных популяциях

Fig. 3. The first column – phase portraits of the system

• (4) at F ( x ) = 1 - x and s₁=s₂=0.5. Other parameter values are shown in the figure. Black and gray circles – trajectory of the system (4) for different initial conditions. The arrows show the trajectory direction .

The second row – dynamics of allele frequencies and abundances of adjacent populations имеют меньший размах (синфазные колебания). В этом случае устойчива периодическая точка, обозначенная как 220 .

Во втором примере на рис. 3b различия в рождаемости не столь существенны, но превосходят бифуркационное значение ( giwi = 3 ). Поэтому при движении к генетической однородности обе популяции при m=0 изначально генерируют близкие циклы, которые в зависимости от начальных численностей могут синхронизироваться, и траектория устремится к периодической точке 202 , расположенной в окрестности прямой x1=x2. При других начальных условиях каждая из популяций будет колебаться с собственной фазой (противофазные колебания), а траектория устремится к другой паре точек 212 , расположенной достаточно далеко от x1=x2. Вместе с тем режим динамики, соответствующий движению к генетической дивер- генции, устойчив (точки E3 и E4), как и в прошлом примере, поэтому данная траектория не приведена на рис. 3 (аналогична показанной на рис. 1).

Дальнейший рост рождаемостей g1 и g2 приводит к тому, что репродуктивные потенциалы giwi каждой популяций для предельных модельных значений q1 и q2 в случае полиморфизма достигают бифуркационных значений и неподвижные точки E3 и E4 теряют устойчивость. Можно сказать, что для такой генетической структуры потеря устойчивости происходит «позже», чем в случае мономорфизма, поскольку из-за понижен- ной приспособленности гетерозигот величины giwi достигают величины 3 для более высоких значений рождаемости. Сценарий потери устойчивости в этом случае, очевидно, аналогичен сценарию для мономорфных состояний популяций с тем отличием, что частоты q1 и q2 могут при определенных условиях начать испытывать небольшие колебания, но лишь для противофазных режимов динамики численностей x1 и x2. Причины такого поведения не до конца ясны и требуют дальнейшего изучения. Примеры режимов, возникающие в этом случае, показаны на рис. 4.

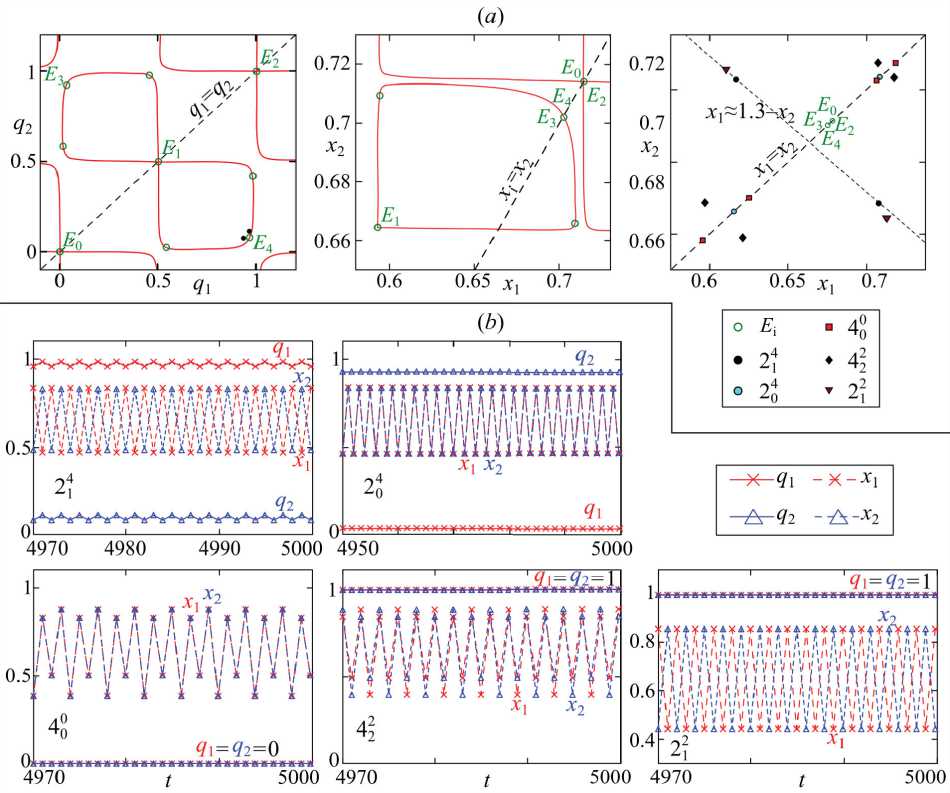
Рис. 4. (a) Фазовые портреты системы (4) при F ( x ) = 1 - x , s 1 =0.6, s 2 =0.5, g 1 =g=3.5 и m=0.02. (b) Примеры циклов в системе (4) при достижении полиморфизма с существенной разницей в частотах аллелей в смежных популяциях (первая строка) и мономорфизма с одинаковыми частотами аллелей (вторая строка)

Pic. 4. (a) Phase portraits of the system (4) at F ( x ) = 1 - x , s 1 =0.6, s 2 =0.5, g 1 =g 2 =3.5 and m=0.02. (b) Examples of cycles in the system (4) at reaching polymorphism with a signifi cant difference in allele frequencies in adjacent populations (first line) and monomorphism with the same allele frequencies (second line)

На рис. 4 a показано, что различие только лишь в интенсивностях отбора s ₁ и s ₂ также вносит определенную асимметричность расположения неподвижных точек, но касается это лишь изначально неустойчивых точек E ₁ и точек, окружающих E ₃ и E ₄. Точки, соответствующие мономорфной популяции, по-прежнему лежат на прямых x ₁= x ₂ и q ₁= q ₂. Точки же, соответствующие генетически неоднородной популяции ( E ₃ и E ₄), теперь не лежат на прямой q ₁=1– q ₂, как в случае полностью идентичных популяций.

На рис. 3 и 4 использовано следующее обозначение циклов: T_i ^j , где число T равно периоду колебаний. Верхний индекс j показывает номер неподвижной точки, из которой сформирован этот цикл и вокруг которой лежат фазовые точки цикла. Нижний индекс i – степень синхронизации динамики численностей x ₁ и x ₂ такая, что , t =1,2,3… При i =0 переменные x ₁ и x ₂ испытывают синфазные колебания, при 0< i < T – противофазные.

Несложно подсчитать, что при указанных на рис. 4 значениях параметров в системе (4) возможно 5 разных режимов динамики численностей x ₁ и x ₂, которые с разными вариантами предельных генетических структур приводят к 10 режимам. В случае однородной генетической структуры в обеих популяциях предельные значения частот q i = q 2 = 0 или 1, а динамика численностей представлена 3 режимами: синфазный 4-цикл (4⁰₀ и 4²₀ ), противофазный 2-цикл (2₁⁰ и 2₁² ) и 4-цикл (4⁰₂ и 4²₂ ). В случае неоднородного распределения q i * q 2 динамика численностей представлена двумя режимами: синфазный 2-цикл (2³₀ и 2₀⁴ ) и противофазный 2-цикл (2₁³ и 2₁⁴ ). Во всех этих случаях, кроме последнего, частоты q ₁ и q ₂ после переходного процесса достигают некоторых стационарных значений и не меняются со временем. В последнем же случае частоты аллелей переходят к синфазному 2-циклу с небольшим размахом колебаний.

Выводы

Таким образом, в работе выполнено обобщение ранее изученной модели эволюции системы двух миграционно связанных популяций с монолокусным отбором. Для этого рассмотрены уравнения динамики численностей каждой популяции, а не величины веса одной из популяций к общей численности, как это было сделано ранее

[5, 10]. Это позволило учесть плотностно-зависимое лимитирование роста численности, которое в работе введено через унимодальную зависимость рождаемости, выражающую гаметопродукцию, от плотности.

В работе рассмотрен случай, когда популяции не отличаются по направлениям отбора, но могут иметь разные интенсивности отбора и рождаемости. Для обеих популяций рассмотрен дизруптивный отбор, при котором гетерозиготы имеют пониженную приспособленность. Показано, что этого достаточно, чтобы обеспечить возможность дивергентного развития популяций. В данном случае каждая популяция при небольших значениях коэффициента миграции и большой интенсивности отбора гетерозигот оказывается полиморфной, т.е. содержит особей с разными генотипами, но на разных участках концентрации гомологичных аллелей будут разными. По всей видимости, именно миграция особей способна как поддержать длительное сохранение этих различий в генотипах (при слабой связи), так сгладить эти различия (при сильной связи).

Были изучены механизмы формирования генетической дивергенции и сопровождающие ее изменения численностей. Было показано, что при движении к одной из возможных предельных генетических структур (мономорфизм или полиморфизм) наблюдаются изменения репродуктивных возможностей каждой из популяций с отличающимися темпами роста и предельными значениями репродуктивных потенциалов. Показано, что при дизруптивном отборе генетически однородные мономорфные популяции имеют более высокий предельный репродуктивный потенциал, чем генетически неоднородные полиморфные популяции. Как следствие, стационарные численности для двух этих генетических структур могут сильно отличаться, а потеря устойчивости происходит при разных значениях параметров. В этом случае система популяций имеет сосуществующие устойчивые и периодические режимы динамики численности или множество сосуществующих режимов с разными периодами и фазами колебаний (мультистабильность).

Работа выполнена в рамках государственного задания Института комплексного анализа региональных проблем ДВО РАН.