Генетическое программирование энергетической эффективности функционирования машинно-тракторных агрегатов

• 1.    Рассмотреть структуру энергозатрат при использовании МТА и определить основной оценочный показатель уровня затрат энергоматериальных ресурсов.

• 2.    Установить тип оптимизационной задачи, количество критериев и определяющие данные критерии, целевые функции.

• 3.    Рассмотреть современные методики решения оптимизационных задач с использованием генетических алгоритмов, исходя из разновидности задачи оптимизации.

Результаты исследований и их обсуждение . Анализ структуры энергозатрат на производство продукции растениеводства показывает, что она имеет три основных составляющих [1]:

• –    экологическую энергию Е Э ;

• –    антропогенную энергию Е ан ;

• –    энергию питания почвы Е П .

Эффективное использование системы машин при выполнении технологических операций относится ко второй составляющей энергозатрат ( Е ан ) на производство продукции растениеводства.

Энергозатраты при использовании МТА для выполнения различных технологических операций в составе машинных комплексов по возделыванию сельскохозяйственных культур определяются двумя основными составляющими:

• -    основные прямые топливно-энергетические затраты;

• - энергозатраты, обусловленные несоблюдением оптимальных параметров и режимов работы агрегатов.

Энергия, потерянная через урожай, может быть определена следующим образом [3]:

Е пот =Е а +Е у ,                                                 (1)

где    Е А – энергия, потерянная при нарушении агросроков выполнения операций, МДж/га;

Е У – энергия, потерянная в связи с уплотнением почвы, мДж/га.

Суммарные энергозатраты при использовании МТА можно определить по формуле

Е мта =Е оПр +Е А ,                                          (2)

где     Е мта – энергозатраты при использовании МТА, мДж/га;

Е опр - основные прямые топливно-энергетические затраты, мДж/га;

Е а — энергозатраты, обусловленные несоблюдением оптимальных параметров и режимов работы агрегатов.

Основные прямые энергозатраты определяются по следующим соотношениям:

Е опр

Ce g .

M ( N e ) ’

Е опр

^СЕ 2 • ^G Т ^M ( N кр ) ^,

где Е_опр – математическое ожидание основных прямых топливно-энергетических энергозатрат;

С Е 1 = ( а Т • К а )/(0,36ц_Т • т ) - коэффициент;

С,₂ = 0,36 тК ^{- 1} ; Е 2                  a

α _Т – энергетический эквивалент дизельного топлива, мДж/кг;

К а – удельное тяговое сопротивление рабочих машин, кН/м;

η _Т – тяговый КПД трактора на рабочем режиме;

т - коэффициент использования времени смены;

M ( N_e ) – математическое ожидание эффективной мощности дизеля, кВт;

M ( N кр ) - математическое ожидание тяговой мощности, кВт;

G Т – математическое ожидание часового расхода топлива, кг/ч.

Нарушение агросроков выполнения операций по возделыванию культур происходит, как отмечалось ранее, при несоблюдении оптимальных параметров и режимов работы МТА и является предметом более детального изучения.

Для определения Е А в работе [3] предлагается использовать выражение:

N " ¹

Z (Сп.WW• Т • n )+ N1 • Cn•W• Т • n

Пi          см см              Пi          см см

Е а =  --------------------;----------------------- ,          (4)

S 0

где С Пi – коэффициент потерь урожая, мДж/га·день;

СП = Y wAу • Q/100,                  (5)

где Y – планируемая урожайность, кг/га;

Δy – потери урожая (%) на 1 день увеличения агросроков выполнения операций;

N i – число целых дней в N¹;

S 0 – объем работы на данной операции, га;

W – производительность агрегата, га/ч;

Q – энергоемкость 1 кг продукта, МДж/кг.

N1 =----S0----

,

W-T -n см nсм где   N1 – число дней, необходимых для выполнения объёма S0;

n см – число смен в одном рабочем дне;

Т см – продолжительность смены, ч.

Определение величины потерь энергии Е А с использованием выражения (4) необходимо осуществлять путем сравнения базового значения производительности W б , которое соответствует номинальному режиму работы МТА, и оптимального значения W опт , которое соответствует оптимальному режиму работы агрегата с учетом негативного влияния колебаний внешней погрузки.

Базовое значение производительности МТА W б и оптимальное значение W опт. необходимо в данном случае определять по выражениям (10) и (13).

Коэффициент, учитывающий степень влияния переменной внешней нагрузки на производительность МТА, определяется по формуле:

—* —

^ W ч = ^W ч / ^W Ч н ,                     (7)

*

где W ч – среднее значение часовой производительности, соответствующее оптимальному нагрузочному режиму двигателя, га/ч;

W ч _н – среднее значение часовой производительности агрегата в области номинального режима.

Работа МТА с отклонением от оптимума загрузки двигателя трактора, установленного с учётом влияния случайных внешних факторов, приводит к снижению производительности, удлинению времени выполне- ния операций технологического процесса и, следовательно, к нарушению агросроков возделывания сельскохозяйственных культур. Нарушение агросроков отрицательно влияет на урожайность, т.е. увеличиваются потери энергии урожая и общее количество энергозатрат процесса производства сельскохозяйственной продукции. Поэтому при повышении эффективности использования МТА с учётом энергозатрат технологического процесса необходимо учитывать спектр факторов, влияющих на обе составляющие процесса и разработать обобщающий критерий, который объединяет и прямые затраты и потери энергии урожая Епот.

Обобщающий критерий оценки влияния оптимальных параметров и режимов работы МТА на энерго- затраты технологического процесса – биоэнергетический КПД оценки антропогенных воздействийηаi определяется по соотношению [3]:

П = ЛЕ . /(ЁE .Л*-  )

ai             ni i i ai     Е мта                             (8)

где

λ Е МТА – оптимальное значение коэффициента оценки величины энергозатрат при использовании

МТА;

∆ Е _пi – прибавка энергопродуктивности при энерготехнологических воздействиях Е аi ;

Е _аi – энергозатраты антропогенных воздействий.

энергозатрат при использовании МТА

Оптимальное значение коэффициента оценки величины λ Е МТА находим по выражению [3]:

2 * =Г /Г.

Л Емта ЕМТА / ЕМТАб,

*

где   ЕМТА – среднее значение энергозатрат при использовании МТА в области оптимального нагрузоч ного режима работы двигателя, мДж/га;

ЕМТАб – базовое значение энергозатрат при использовании агрегата в области номинального ре- жима работы двигателя, мДж/га.

Обобщающий критерий определяется с учетом использования оптимальных значений показателей двигателя и трактора, входящего в состав МТА. Исходя из того, что энергозатраты использования агрегатов определяются, прежде всего, расходом топлива и производительностью (которая зависит от эффективной мощности двигателя или тяговой мощности трактора), можно сказать, что задача нахождения оптимальных параметров и режимов работы МТА является двухкритериальной. Иначе говоря, рассматривается многокритериальная оптимизация по двух ведущим и в то же время противоречивым критериям. Целевые функции поставленной оптимизационной задачи, определяющие характер и количество критериев, могут быть представлены в виде следующих (11), (12), (14), (15).

Математическое ожидание часовой производительности МТА определяем следующим образом [4]:

М(W ч ) _ С ,,[ М(N е ) ]

где M (,_Ч ) - математическое ожидание производительности агрегата, га/ч;

С , , = 0,3в П т т К -¹ ;

η _T – тяговый КПД трактора;

K_a – удельное сопротивление агрегата, кН/м;

τ – степень использования времени работы агрегата, кН/м;

M ( N _е) — математическое ожидание эффективной мощности двигателя, кВт.

Математическое ожидание эффективной мощности двигателя в выражении (10) находим с помощью формулы [5]:

М ( N е ) = f ( M k ) = 9550

1 ^0,5 ⁽ a M + b ^Mk + b a M ) +⁽ a i ^Mk + b i ^Mk + b i ° M Ф ⁽ * н ) +

_+ ( a 2 M k + b ₂ m} + b₂&l ф ( t n ) - & m { b i ^ ( t н ) M k + b 2 ^ ( t n ) M k } _ (ii)

где

М к – текущее среднее значение крутящего момента, Н∙м;

1/ * Н 1 2/

Ф ( t_H ) = ( 2 n )^{- 22} j е ²² dt - функция Лапласа для Y = f ( M K ) ;

^ ( t_Н ) = ( 2 n ) ¹² exp ( - 0,5 t H ) - плотность распределения аргумента t н ;

1/ t n 1 2

Ф ( t_П ) = ( 2 п )^{- 21} j е ²² dt - функция Лапласа для Y = f ( M K ) ;

^ ( t_П ) = ( 2 п ) ¹² exp ( - 0,5 t П ) - плотность распределения аргумента t п ; _t _ M н - M к    _М П - M к.

¹ Н =               , ¹ П =               ;

аМ         аМ аМ - стандарт крутящего момента, Н-м;

M Н – номинальное значение крутящего момента, Н∙м;

M П – предельное значение крутящего момента, Н∙м;

a 1, bi, a ,b , a2,b2 - расчетные коэффициенты, определяемые при аппроксимации характеристики двигателя в зависимости от крутящего момента на коленчатом валу.

Для расчета математических ожиданий часового расхода топлива двигателя постоянной мощности используем следующее выражение:

Gt = 0,5 ( a + b Мк ) + ( a

*

' 1

*              *   *                 */Ч*

+ ^b 1 Мк Ф ⁽ tн ) + ^{( a} ₂ ^{+ b} ₂ ^Мк ) Ф ⁽ tп ) - G P ^{{( b} 1 ^ ⁽ tн ) ^{+ b} ₂ ^ ⁽ tп ^)}, (12)

где G_T – математическое ожидание часового расхода топлива, кг/ч;

a i, b i, a 2, b 2, a , b - расчетные коэффициенты, определяемые при аппроксимации тяговой характеристики трактора по расходу топлива.

Для расчета математических ожиданий часовой производительности МТА в зависимости от переменной силы тяги трактора используется следующее выражение [4]:

М (W Ч ) = с , 2 [ М ( N КР ) ]

где    М ( , Ч ) - математическое ожидание производительности агрегата, га/ч;

• С , ₂ = 0,36^ ;

K_a – удельное сопротивление агрегата, кН/м;

• т - степень использования времени работы агрегата;

М ( N _КР ) - математическое ожидание тяговой мощности, кВт.

Математическое ожидание тяговой мощности в выражении (13) находим следующим образом [6]:

М ( N КР ) = f ( Р кр ) =

0,5 ( a ° P КР + b ° P КР + b ° О

°"^         ° "^2        °    2

+ ( a 2 P кр + b 2 P кр + b ^ o р

■ р ) + ( a j P кр + b P кр + b с р ф( ( в н ) +

^

О р { №в н ) P КР + b ° rtв п ) P КР } J ,   ₍₁₄₎

где вп

Ф( в п ) = ( 2 п )^{- 12} J е

d e - функция Лапласа для аргумента в п ;

^в н

Ф( в н ) = ( 2 п )^{- 12} J

е ^/2 d e - функция Лапласа для аргумента в н ;

ф ( в _п ) = ( 2 п ) - ¹² exp ( - 0,5 в П ) — плотность распределения аргумента в п ;

^ ( в _н ) = ( 2 п )^{- 12} exp ( - 0,5 в Н ) — плотность распределения аргумента в н ;

P кр - текущее среднее значение силы тяги, кН;

с _р - стандарт силы тяги трактора;

о _ ¹ КР . П

Рп =

^

^с р

^{P КР}  о _ ^РКР . Н

, ^в н =

-

^с р

P КР

а р b 1 , a , b , а ₂, b ₂ - расчетные коэффициенты, определяемые при аппроксимации тяговой характеристики трактора;

P кр . п - значение силы тяги трактора на данной передаче, соответствующее предельному крутящему моменту, кН;

P кр . н - номинальное значение силы тяги трактора на данной передаче, кН.

Аналогично рассчитываются математические ожидания часового расхода топлива G T [6]:

G t = 0,5 ( a ’ + b ’ P kp ) + (a * + b P kp )ф ( t н ) + ( a 2 + b * P kp )Ф ( t . ) - О р {( b’ ^ ( t . ) + b > ( t . )},

(l5)

где G T - математическое ожидание часового расхода топлива, кг/ч;

• a * , b * , a 2 , b 2 , a * , b * - расчетные коэффициенты, определяемые при аппроксимации тяговой характеристики трактора по расходу топлива.

В настоящее время для решения задач многокритериальной оптимизации все большее распространение получают эволюционные алгоритмы (ЭА). Одновременная многокритериальная оптимизация нескольких многомерных и противоречащих друг другу целевых функций отличается от классической одномерной оптимизации в том, что она редко допускает единственное решение поставленной задачи.

Чаще всего проблемы многокритериальной оптимизации характеризуются многими альтернативными подходами и решениями, которые могут оцениваться равноправно.

Эволюционные алгоритмы (ЭА) хорошо зарекомендовали себя как при решении однокритериальных задач, так и при решении многомерных, многокритериальных и альтернативных задач оптимизации. Это преимущество ЭА перед традиционными методами оптимизации заключено в их механизме. Многочисленные индивидуумы (решения задачи) и обширные популяции (множества решений задачи) могут вести поиск необходимого количества решений одновременно и параллельно. Методика ЭА позволяет с высокой эффективностью решать сложные задачи, имеющие такие особенности, как унимодальность, разрозненные допустимые области, наличие разнохарактерных переменных, алгоритмически заданные целевые функции. Эффективность ЭА наиболее высока при решении многокритериальных задач, которые, как правило, трудно решить традиционными или классическими методами.

На основе общего эволюционного алгоритма и его составляющих многокритериальных генетических алгоритмов (ГА) разработан ряд методов решения оптимизационных задач. Наиболее распространены в настоящее время четыре разновидности ГА (наряду с другими), а именно:

VEGA – Vector Evaluted Genetic Algorithm [7, 8];

FFGA – Fonseca and Flemming's Multiobjective Genetic Algorithm [7, 8];

NPGA – Niched Pareto Genetic Algorithm [7, 8];

SPEA – Strength Pareto Evolutionary Algorithm [8].

Для решения представленной в статье двухкритериальной задачи оптимизации энергозатрат технологического процесса достаточно эффективным может быть метод VEGA.

Метод VEGA предложил в 1984 году Шаффер. Он предусматривает расширение традиционного ГА за счет использования векторных оценок степени пригодности индивидуумов и возможности параллельной оценки популяций по каждому из критериев в отдельности. Таким образом, осуществляется одновременная оптимизация по всем целевым функциям.

Метод VEGA относится к методам параллельных популяций или множества решений задачи, отобранных по каждому из частных критериев, т.е. селекция или выбор наилучшего решения в соответствии с его пригодностью (соответствия критерию) производится для каждого критерия в отдельности.

Этап селекции в данном ГА протекает таким образом, что в каждом поколении создается некоторое количество подпопуляций с помощью пропорциональной селекции для каждой целевой функции. То есть в задаче с К критериями создается К подпопуляций размером N/К, где N – размер всей популяции, исходя числа целевых функций. Далее подпопуляции смешиваются для получения новой популяции размером N, после чего ГА использует операторы мутации и рекомбинации (скрещивания индивидуумов).

Механизм селекции (повторного использования хороших решений) и назначения пригодности в методе VEGA схематически выглядят следующим образом (рис.).

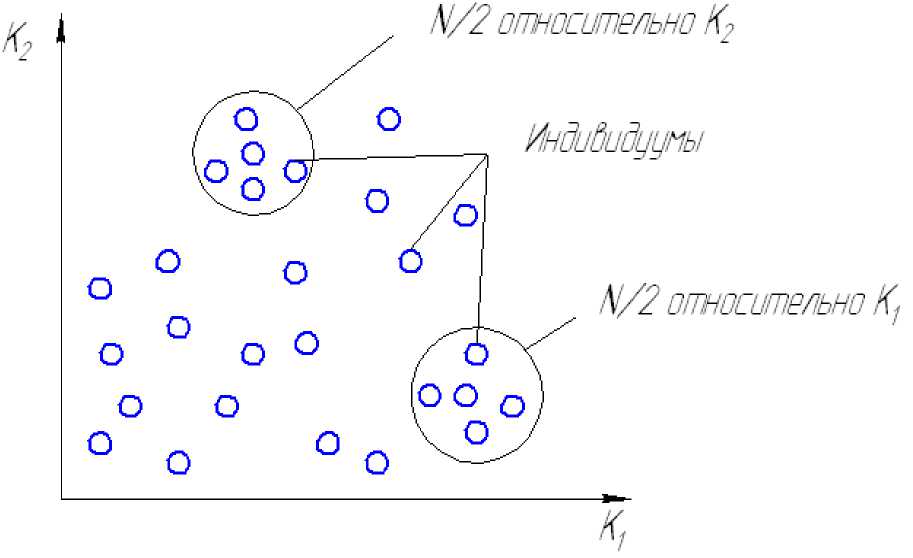
Пропорциональная селекция в методе VEGA: К ₁ и К ₂ – критерии

На рисунке представлена двухкритериальная задача. Для каждого из критериев создается подпопуляция размером N/2, куда индивидуумы отбираются с помощью пропорциональной селекции относительно пригодности по каждому критерию в отдельности. Затем подпопуляции смешиваются для получения общей популяции размером N. Далее осуществляются этапы скрещивания и мутации. Данный ГА может использовать принцип паретооптимальности (использование множества Парето) при решении многокритериальной задачи. В представленной на рисунке схеме применительно к задаче оптимизации параметров и режимов работы МТА критериями К1 и К2 могут быть часовой расход топлива Gт и эффективная мощность двигателя Ne, а также часовой расход Gт топлива и мощность трактора NKpна данной передаче.

Более эффективным по некоторым параметрам может быть признан метод SPEA. Он отличается от трех остальных тем, что использует Парето-доминирование для назначения степени пригодности выбранным решениям задачи, а также тем, что недоминирумые в популяции индивидуумы хранятся в специальном внешнем множестве. Кроме того, SPEA использует механизм кластеризации (разбиение выборки объектов на подмножества, называемые кластерами или однородными группами объектов со схожими свойствами) для уменьшения количества индивидуумов, хранящихся во внешнем множестве [8].

Преимущества метода SPEA по сравнению с другими (VEGA, FFGA, NPGA) следующие:

• 1.    Сочетание вышеназванных подходов в одном алгоритме.

• 2.    Значение пригодности индивидуумов всей популяции оценивается с учетом пригодности индивидуумов внешнего множества, пригодность остальных не учитывается.

• 3.    В селекции принимают участие все индивидуумы, в том числе «лучшие» из внешнего множества.

• 4.    В методе SPEA используется механизм ниширования, в котором деление общей пригодности осуществляется на основе парето-доминирования.

Исходя из особенностей и преимуществ метода SPEA, представленный выше метод VEGA может быть усовершенствован для более эффективного функционирования.

Полученные с использованием ГА оптимальные характеристики двигателя и трактора, а также соответствующие им показатели работы МТА, могут позволить достаточно эффективно определять значение

∗ критериев λЕМТА и ηаi .

• 1.    На основе анализа энергозатрат при использовании МТА предложен оценочный показатель уровня затрат энергоматериальных ресурсов.

• 2.    Рассмотрены предпосылки к обоснованию типа оптимизационной задачи; установлены количество критериев и определяющие данные критерии целевые функции.

• 3.    Представленные современные методики решения оптимизационных задач с помощью многокритериальных генетических алгоритмов позволят эффективно решать проблему снижения энергозатрат при использовании мобильных машинно-тракторных агрегатов.

• 1.    Цугленок Н.В. Энерготехнологическое прогнозирование: учеб. пособие / Краснояр. гос. аграр. ун-т. -Красноярск, 2004. – 276 с.

• 2.    Агеев Л.Е. Основы расчета оптимальных и допускаемых режимов работы машинно-тракторных агрегатов. – Л.: Колос, 1978 .

• 3.    Журавлев С.Ю., Цугленок Н.В. Оценка влияния оптимальных показателей работы МТА на энергозатраты технологического процесса// Вестн. КрасГАУ. – 2010. – № 10. – С. 146–151.

• 4.    Агеев Л.Е., Шкрабак В.С., Моргулис-Якушев В.Ю. Сверхмощные тракторы сельскохозяйственного назначения. – Л.: Агропромиздат, 1986. – 415 с.

• 5.    Журавлев С.Ю. Влияние переменных внешних факторов на производительность машинно-тракторных агрегатов // Вестн. КрасГАУ. – 2011. – № 7. – С. 148–153.

• 6.    Журавлев С.Ю. Оценка эффективности функционирования мобильных сельскохозяйственных агрегатов с использованием тяговой характеристики трактора // Вестн. КрасГАУ. – 2011. – № 9. – С. 146–151.

• 7.    Терсков В.А. Модели функционирования и методы оптимизации структуры многопроцессорных вычислительных систем: монография. – Красноярск: СибЮИ МВД России, 2001. – 335 с.

• 8.    Гуменникова А.П. Адаптивные поисковые алгоритмы для решения сложных задач многокритериальной оптимизации: дис. … канд. техн. наук. – Красноярск, 2006. – 129 с.