Геодинамическая модель глубинного строения палеосубдукционной зоны на восточной окраине Русской палеоплиты и распределение месторождений нефти и газа

Известно, что построение надежной физико-математической модели глубинного строения любого региона имеет существенное значение как в теоретическом плане – для исследования тектонического строения этого региона, так и в прикладном – для прогнозирования поисков полезных ископаемых на исследуемой территории. Постановка задачи данной статьи связана с разработкой методики оценки некоторых глубинных гидродинамических параметров мантии Земли на основе определения расстояния от вулканической островной гряды, использующей известную гипотезу о том, что квазилинейные геолого-тектонические зоны представляют собой полосчатые структуры, которые параллельны горному вулканическому поясу, расположенному у ребра мантийного суб-дукционного клина, и могут находиться в пределах некоторого интервала расстояний от горного вулканического пояса. Первые исследования в этом направлении были сделаны зарубежными коллегами на примере суб-дукционной зоны в районе литосферной плиты Наcка (Barazangi et al., 1976), а также по несколько другой, но подобной методике оценки (Karig, 1971). На территории России имеется несколько регионов, где по параметрам расположения островных вулканических дуг экспериментально могут быть проверены основанные на рассматриваемой гипотезе теоретические расчеты углового направления субдукционного погружения литосферных или палеолитосферных плит. Одним из самых важных регионов России, где можно показать преимущество расчетов геодинами-ческих параметров мантии в зоне палеосуб-дукционного клина для прогноза зон расположения месторождений нефти и газа, является территория Западной Сибири (рис. 1).

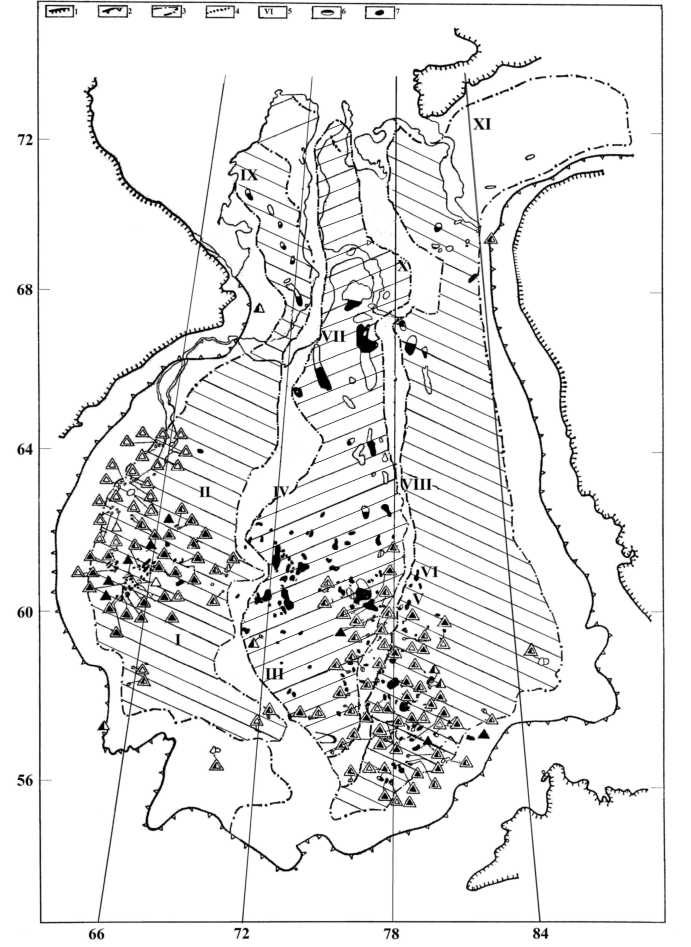
Рис.1. Схема полосчатой структуры расположения субмеридиональных геолого-тектонических поясов Западно-Сибирского региона (заштрихованы). Геолого-тектонические (в том числе нефтегазоносные) пояса связаны с тепломассопереносом вещества по серии глубинных литосферных разломов от центров пар конвективных противоположно вращающихся вихрей Карига, возникших в астеносфере, прилегающей к палеосубдукционному мантийному клину, расположенных под «подошвой» литосферного слоя Уральского палеоокеана (Западно-Сибирской палеоплиты): 1 – тектонические границы Западно-Сибирского региона; 2 – границы Западно-Сибирской углеводородной провинции; 3 – номера геолого-тектонических зон, составляющих пояса определенного вида углеводородных месторождений (нефть или газ или конденсат): I–II–IX – Приуральско-Фроловско-Южно-Ямальский газовый пояс, III–IV–VII–X – Каймысовско-Среднеобско-Надым-Пурский нефтяной пояс, V–VI–VIII – Васюган-Пайдугинско-Пур-Тазовский конденсатный пояс, 4 – границы геолого-тектонических зон; 5 – номера геолого-тектонических зон; 6 – контуры месторождений углеводородов; 7 – обозначение разных типов месторождений углеводородов ( Порфирьев, 1982 )

Существенной особенностью локальных и региональных геолого-тектонических зон Зауралья и Западной Сибири является периодичность их пространственного расположения вдоль широтного направления (Ступак,

Берзин, 2001). Так, например, вытянутые в меридиональном направлении эти периодические региональные геолого-тектонические зоны представляют собой своеобразные полосы шириной ~ 300 км, параллельные

Уральскому хребту и расположенные с периодичностью примерно 300 км (Порфирьев, 1982).

Распределение гравитационных аномалий в редукции Буге (Петров, 2001) поперек поля напряжений Уральской геотектонической системы и ряд геологических аргументов в работе М.Г. Когана и Р.Ю. Кукулиевой (1988) свидетельствуют, что после формирования Уральского палеовулканического пояса в пермский период эволюционного развития Земли (295 – 240 млн лет назад) происходило взаимное поддвигание литосферы Русской палеоплиты (РП) под литосферу Восточно-Сибирской палеоплиты (ВСП) в районе окраинного палеоокеанического бассейна – Уральского палеоокеана, примерно соответствующего современному расположению Западно-Сибирской низменности (рис. 2).

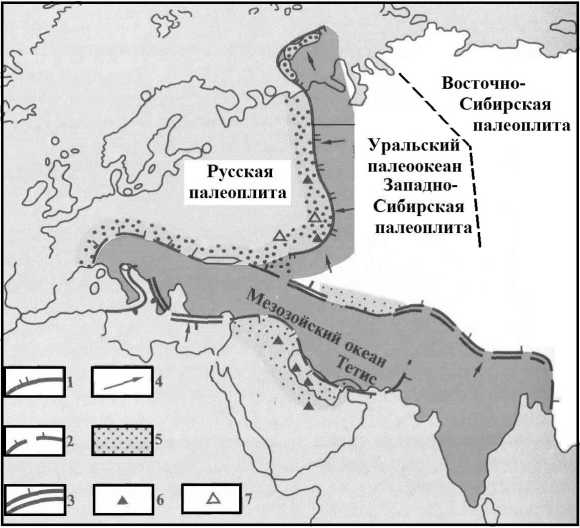
Рис. 2. Палеотектоническая реконструкция формирования Уральского палеовулканического пояса в процессе формирования палеосубдукци-онной зоны при палеотектонической коллизии Русской и Восточно-Сибирской палеоплит (ВСП). Зоны палеосубдукции: 1 – палеозойские; 2 – мезозойско-кайнозойские; 3 – ныне действующие; 4 – зона сжимающих напряжений при взаимном поддвиге Русской и Восточно-Сибирской литосферных палеоплит в палеозойский период эволюции Земли; 5 – зона расположения Уральского палеовулканического пояса; 6, 7 – расположение некоторых крупных месторождений полезных ископаемых ( Арешев, Гаврилов и др., 1997)

Хорошо известна аналогичная современная субдукционная зона, которая в данный период только развивается в пределах Охотского моря – окраинной зоны Тихоокеанской литосферной плиты, поддвигающейся под литосферу Азиатского континента (рис. 3) (Гайнанов, 1991).

Z^, мГал

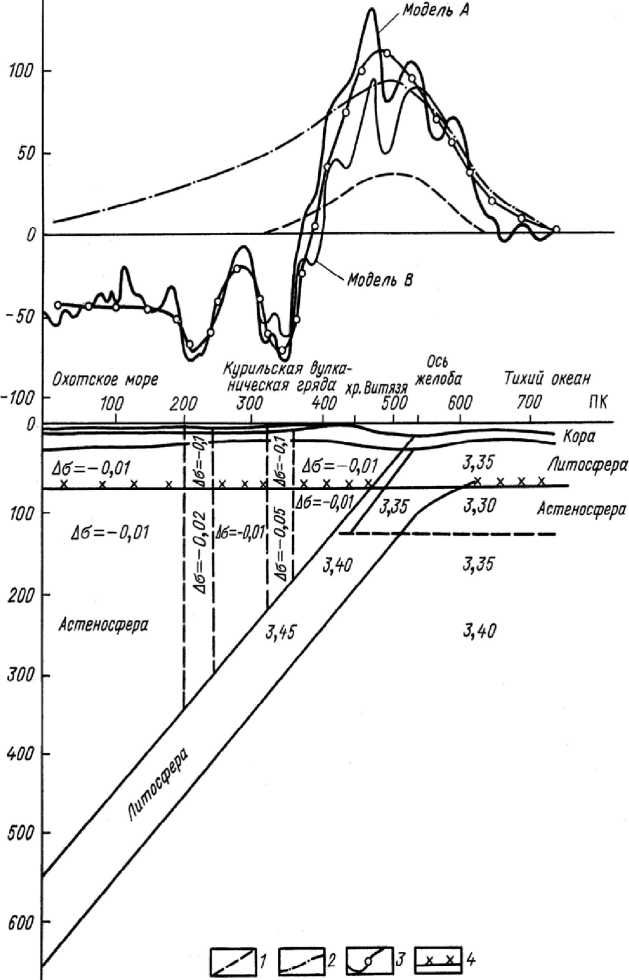
Н,км

Рис. 3 . Плотностная модель астеносферы и зоны субдукции Тихоокеанской литосферы в переходной зоне Охотское море – Курильская гряда – Тихий океан ( Гайнанов, 1991 ) . Кривые «модель А» и «модель В» – остаточные мантийные аномалии силы тяжести – dg после исключения из наблюденной аномалии силы тяжести влияния изменения мощности слоев земной коры, полученной по сейсмическим данным; 1 – гравитационный эффект эклогитового слоя литосферы ( Ла =+0.02 г/см 3 ), 2 - гравитационный эффект погружающейся плиты литосферы ( Ла =+0.05 г/см ³ ), 3 – суммарный гравитационный эффект плотностных неоднородностей литосферы и астеносфероы, 4 – «подошва» литосферы

На рис. 3 хорошо видны после основного максимума, расположенного над осью желоба, два экспериментально зафиксированных минимума значений поля силы тяжести, свя- занные с вертикальными зонами изменения плотности пород в астеносфере, под Охотским окраинным бассейном. По мнению некоторых исследователей, эти вертикальные зоны разуплотнения в астеносфере также связаны с конвективными ячейками Карига, которые образуют вертикальные зоны теп-ломассопереноса вещества из мантии к поверхности Земли.

Предполагая, что геолого-тектонические зоны на территории Западно-Сибирской низменности (Уральский палеоокеан) образовались над восходящими потоками нагретого вещества (процессы тепломассоперено-са), возникшими над конвективными вихрями Карига в палеосубдукционном мантийном клине, можно оценить некоторые геоди-намические параметры мантии в зоне пале-осубдукции (скорость палеосубдукции, угол наклона палеомантийного клина, скорость смещения конвективных вихрей Карига во времени) в районе палеотектонической коллизии Русской и Восточно-Сибирской литосферных плит в палеозойский период развития Земли, которые позволили создать большое количество местрождений нефти, газа, газоконденсата на этой территории.

В соответствии с имеющимися научными представлениями о развитии этого региона (Порфирьев, 1982; Арешев, Гаврилов и др., 1997; Павленкова и др., 2014) мы хотели показать, что конвективная зона шириной 1000 км в палеомантийном клине (рис. 4) в палеозойский период эволюции Земли была расположена на восток от Уральского палеовул-канического хребта, что соответствует образовавшимся там (на территории Западной Сибири) линейным геолого-тектоническим зонам, показанным выше на рис. 1.

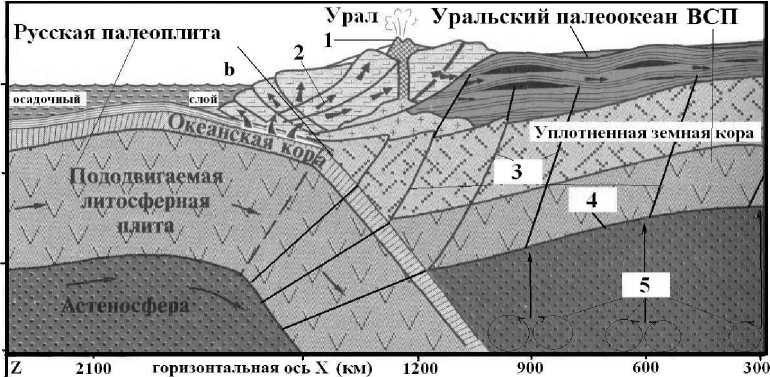
Рис. 4. Схематический глубинный разрез астеносферы и зоны палеосубдукции, образовавшейся в процессе палеозойского погружения литосферы Русской палеоплиты (РП) в переходной зоне Уральского палеоокенана (территория Западно-Сибирской плиты (ЗСП): 1 – Уральская палеовулканиче-ская гряда; 2 – направление движения конвективного потока нагретого вещества (в том числе и углеводородов) из мантии к поверхности Земли по зонам напластования и по глубинным литосферным разломам; 3 – глубинные литосферные разломы, уходящие корнями в астеносферу, связанные с зоной субдукции; 4 – «подошва» литосферы Уральского палеоокеана (Западно-Сибирской палеоплиты) в палеозойский (Pz) период эволюции Земли; 5 – схематическое изображение расположения трех пар конвективных (противоположно вращающихся в паре) вихрей Карига, создающих в центре пары конвективных вихрей восходящие к поверхности Земли потоки разогретого мантийного вещества (тепломассоперенос) (в астеносфере, прилегающей к зоне субдукционного клина, образованного между «кровлей» литосферы субдуцирующей Русской палеоплиты и «подошвой» литосферы Восточно-Сибирской палеоплиты (ВСП). Горизонтальная ось (x) на данном схематическом глубинном разрезе отображает важный параметр – горизонтальное расстояние (300 км) между центрами трех пар конвективных вихрей Карига в палеосубдукционном мантийном клине. На вертикальной оси (z) на данном схематическом глубинном разрезе показаны глубинные отметки расположения различных палеослоев земной коры и верхней мантии в палеозойский период эволюции Земли без мощного слоя современных осадочных пород на Русской плите, соответствующие 0, 30, 60, 90 км

По нашему мнению, конвективные вихри возникали над погруженной Русской палеоплитой в астеносфере над мантийным клином. Конвективные вихри Карига (или просто вихри Карига), поскольку их может быть несколько, при достаточно пологой зоне субдукции должны располагаться в мантии между субдуцирующим литосферным блоком восточного обрамления Русской палеоплиты и Восточно-Сибирской палеоплиты в астеносфере под литосферой Уральского палеоокеана. Иными словами, вихри Карига обычно должны быть расположены в мантийном клине (рис. 4) между «кровлей» субдуцирующей плиты и «подошвой» плиты, под которую происходит суб-дукция. Конвективные вихри Карига в пале-осубдукционном мантийном клине обычно бывают расположены парами и закручены навстречу друг другу. Один конвективный вихрь из пары закручен по часовой стрелке, а другой – против. Между этими двумя вихрями расплавленной мантии образуется восходящий мантийный поток тепла и вещества (тепломассоперенос). Он и выносит по глубинным литосферным разломам простейшие углеводороды (Н 2 , СО 2 , СН 4 ) в приповерхностные зоны их накопления и последующего преобразования (различного типа геологотектонические «ловушки») в «осадочном» слое Земли (Сефуль-Мулюков, 2012). В нашем случае, при погружении Русской палеоплиты под Восточно-Сибирскую палеоплиту в палеозойский период эволюции Земли, существовали три пары конвективных вихрей Карига. Причем каждая конвективная ячейка, состоявшая из пары противоположно вращающихся конвективных вихрей Карига, имела средний горизонтальный размер около 300 км. Все три пары конвективных вихрей Карига должны были быть расположены в палеомантийном клине общей протяженностью в горизонтальной проекции на поверхность Земли около 1000 км к востоку от Уральского палеовулканического пояса и образовывать соответствующую им трехсоткилометровую геологотектоническую зональность на территории Западно-Сибирской палеоплиты, сохранившуюся до наших дней (рис. 1).

Рассмотрим модель палеомантийного клина между «подошвой» Западно-

Сибирской палеоплиты и верхней поверхностью («кровлей») субдуктирующей Русской палеоплиты (рис. 4), в результате относительного движения Русской палеоплиты на восток пододвигающейся под углом в со скоростью V . Верхнюю поверхность («кровлю») субдуктирующей Русской палеоплиты в первом приближении будем считать наклонной полуплоскостью ( z = x * tg в ) а «подошву» Западно-Сибирской палеоплиты – горизонтальной полуплоскостью ( z = 0) соответственно, где x – горизонтальная ось, соответствующая почти горизонтальному направлению «подошвы» Западно-Сибирской палеоплиты, а ось z направлена вертикально вниз. Материал мантийного клина считаем однородной несжимаемой жидкостью с постоянным коэффициентом вязкости П _с , равным его среднему значению. Движение вещества в мантийном клине определяется формулами (Schubert, Turcotte, Olson, 2001; Turcotte, 2002), а уравнение стационарного распределения абсолютной температуры T в мантийном клине при бесконечном числе Прандтля в приближении Буссинеска имеет вид ( Vx , Vz – компоненты скорости вдоль осей x и z )

( V x xd x X T +( V z * d z X T =( x *T x ) + [ T k² / ( 2* П с )], (1) где T ik - тензор вязких напряжений, символ d обозначает частную производную по координатам, / — коэффициент температуропроводности, Л - оператор Лапласа. Согласно (Turcotte, 2002), имеем

U = V_x = д щ /dz = - [ D * arctg ( x /z )] + { x x [( C _x + D z )] / (x ² + z ² )]} – B,

W = V_z = д щ /dx = - [ C * arctg ( x /z )] + { z x [( C x + D z )] / (x ² + z ² ) ] } – A ,                 (2)

T ik ² / (2 x n ) = [(4 x n c ) x ( C z - D x ) ² ] / / (x ² + z ²)² ,                                          (3)

где при условии непроскальзывания при z = 0 и z = x * tg в на границах мантийного клина

A = V * { [( в * ( п / 2) * sin в ] / [в² - sin ² в ] };

B = V * { [(п / 2) - в ] * sin в — [ в * ( п / 2) * cos в ] } / [ в 2 - sin ² в ];

C = - V * { [ в * sin в ] / [ в ² - sin ² в ] };

D = V * { [ ( в * cos в) - sin в ] / [ в 2 -sin ² в ] }.                                         (4)

Отметим, что при в < (п / 4) мощность (3) диссипативного тепловыделения максималь- на у поверхности субдуктирующей литосферы, т.е. у нижней границы мантийного клина.

Граничные условия в уравнении (1) для температуры есть T = T m при z = 0 и z = x х tg в , где T m = 1500^o K - температура субсолидуса. Граничные условия T = T m вдали от ребра мантийного клина (при x -> да) также справедливы, поскольку тепловая энергия, соответствующая температуре, отличной от T m , на достаточном удалении от хребта передается к литосферным плитам, т.к. диссипативное тепловыделение при x -> да спадает до нуля.

Формула (1) показывает, что максимальная температура T max в мантийном клине достигается у поверхности погружающейся плиты и с точностью ~ 10% может быть представлена аналитической формулой T max = T m + {( п C XV 2 k ) X (1/[ F+ ( GxVXx/ % )]}, (5) где F и G - функции угла субдукции в , которые при ( п / 9) <  в < ( п / 4) могут быть представлены приближенными интерполяционными формулами

F = - 2.70 + 15.75 х р ; G = — 2.35 х 10 '³ + 1.27 х 10 ^-2 х р ,                                (6)

где k = 4 х 10⁵ эрг / смс,К - коэффициент теплопроводности пород астеносферы, х = [ k / ( р- c p )] = 10^-2 см² / с , р = 3.30 г / см ³ - плотность пород астеносферы, c p =1.2 х 10⁷ эрг / ( г ' К ) -удельная теплоемкость пород. Согласно (1), ( T max - T m ) пропорционально среднему коэффициенту вязкости Ц _с. Например, при П с =10²¹ Пас = 10²² П, в = 30 ° , V = 10 см / год , x = 100 км, согласно (5)-(6), величина ( T_max -T_m ) ~ 400^o К.

В мантийном клине возможны конвективная и термическая неустойчивости, вызываемые перепадом ( T max - T m ) температуры и возможной (не учитываемой выше) зависимостью вязкости от температуры. Исследуя эти неустойчивости, будем считать угол в субдукции литосферы Русской палеоплиты малым, а вынужденное течение в мантийном клине близким к плоскопараллельному. Если возмущения v _x , v y , v _z компонент скорости, p - давления и 0 - температуры зависят от пространственных координат x, z и времени t как

( v x , V y , V z , p , 0 ) = [ u (Z) , v ( Z), wZ\ p ( Z) , 0 О х exp [ y хt + i ( xхk x + ухк у - tх_a) )] ,   (7)

где Z= (z / x) и в нулевом приближении у и а не зависят от x, при этом ось у направлена вдоль простирания Уральского палеовулка-нического хребта и коэффициент вязкости (п ) зависит от температуры (Т) как п = п0 х exp Z ; Z = (E* + Р х V*) / ( R х T ) (8) (где E* и V* - энергия и объем активации, R - универсальная газовая постоянная), то с учетом dx = dx - (z/ x) хд^ ;

d z = (1 / x )*d z ;

d ² xx = d ² xx — 2 х (Z / x ) х д + 2 х ( Z / x ² ) * d z + ( Z ² / x ² )*d ² zz ;

d ² zz = ( 1 / x ² ) * d ² zz ;

пренебрегая при z << 1 величиной z , для возмущений (11) имеем i kx u + i ky v + w' /x = 0,                       (9)

0 = - ik_xхр - 2 х п хk_x ² хи- п хk y хи-k x хk_y хv

+ { п х [ - С х (0 /xхT) хи’+ ( и'/x ) +i k x хw ]}'/ x , (10) 0 = - i k_yхp - 2 х п хk y хv - п хk_xхk_yхu + { п х [( v'/ x ) + i k_yхw ]}' / x ,                               (11)

0 = - (p'/x ) - ( а хдх р х 0) + п х {( i k_x х и’/x ) -( k x ² хw ) - [ i k x XU'х ^х 0 / xхT) ] +

{ п х [( i k y хv'/x ) - k y ² хw ]} + 2 х ( n хw’ )' / x ² , (12) р хc p х {( у х 0) - ( iх_юх 0 ) + ( wхT уx + ( i k x х их 0 ) + [( Wх 0 ') / x ]} = k ( 0 )'' / x ² - k ² ( 0 ) +

[(4 х п хD ² х £ х 0) / ( x² *T) ] + 4 х п хDх {[( и'х £ х 0 ) / ( xхT) ] - ( u' / x ) - ( i k x хw )} / x ,             (13)

где (9)-(13) есть соответственно уравнение неразрывности, три компоненты уравнения движения и уравнение переноса тепла, а штрих обозначает производную по z • Для решения системы (9)-(13) вводим новые неизвестные функции Z :

У 1,2 = U ^Re,Im , у 3,4 = V ^Re,Im , У 5,6 = W ^Re,Im , У 7 = п х

{иRe / [x - kx х wIm - U' х Z х (0 Re / xхT)]}, у8 = п х {иIm / [x + kx х wRe - U’ х Z х (0Im / xхT)]}, у9 = п х [vRe / (x - ky х wIm)], ую= п х [VIm / (x + ky х wRe)], у 11= pRe - (2 хп х w’Re / x ), у 12 = pIm

-

(2 х п х w' ^Im / x ),     у 13,14 = 0 ^Re,Im , у 15,16 = X х

0 ^Re,^Im .                                                 (14)

Уравнения (9)-(13) относительно функций (14) превращаются в систему 1-го по- рядка:

у' 1 = ( xхk x ху 6 ) + [( xху 7 ) / п ] + ( Z хU'/T) ху 13 ; у' 2 = - ( xхk x Xy 5 ) + [( xхy 8 ) / п ] + ( Z хU^,/T)ху 14 ;

у' 3 = ( xхk y Xy 6 ) + [( xхy 9 ) / п ]; у' 4 = ( xхk y Xy 5 ) +

[( x ху 10 ) / п ]; у' 5 = ( x хk x ху 2 ) + ( x хk y ху 4 );

у'6 = - (x Xkx ху 1) - (x Xky ху3); у'7 = xхпх[(4 хk2x+k2у) ху 1] + (3 ^xхпхkxXky ху3) - (xх kxху 12); у'8 = xхпх[(4хk2x+k2у)ху2] +

(3 ^xх п хk x Xk y ху 4 ) + ( xхk x ху 11 );

у' 9 = х* ц * [(4 xk ² y +k ² x ) xy з ] + (3 *x* n xk x xk y xy 1 ) - ( xxk y xy 12 );

y' 10 = xx ^ x [(4 xk ² y +k ² x ) xy 4 ] + (3 Ххх ц xk x xk y xy 2 ) + ( xxk y xy 11 );

y' 11 = — (xxkxxy8) - (xxkyxy 10) - (axpxgxxxy 13); y' 12 = (x xkx xy 7) + (x xky xy 9) - (axpxgxx xy 14); y'13,14 = y'15,16 / X , y'15 = [x2 x(y + kx2 xx) xy 13] + [x2 x (ф-(kx x U) y 14] + [(x xT') xy5] - [(4 xy 13 xnxD2 x Z) / (pxcpxT)] + [(4xy7xxxD) / (pxcp)] + [( y 15x xxVxO / (xx^)]; y'16 = [x2 x(y + kx2 xx) xy 14] - [x2 x (a)- (kx x U) y 13] + [(x xT') xyб] - [(4 xy 14 xnxD2 x^) / (pxcpxT)] + [(4xy8xxxD) / (pxcp)] + [( y 16x xxVxO / W)] , (15)

где подставляем W = ( Z 2 x V / в ) = 0 при Z <<  1 ( V - скорость субдукции). Свободные граничные условия для уравнений (15) в терминах неизвестных (14) запишутся в виде y 5,6,7,8,9,10,13,14 = ⁰ при ^Z = 0, t = tg ^в .      (¹⁶)

Для оценки величин y и а примем коэффициенты в формуле (15) постоянными, равными их средним значениям, в частности П = n . Тогда задача, представленная в формулах (15) - (16), имеет решение: yi = A i x {[ _cos ^sm ] A x Z } с A = [ n / (tg в )], i = 1, 2... 16.

Найдем условия существования нетривиального решения при k_y = 0. В этом случае конвекция возникает в форме вихрей Карига, а уравнения для y ₃,₄,₉,i₀ образуют отдельную подсистему, из которой следует, что y ₃,₄,₉,i₀ = 0, т.е. возмущения скорости и сдвиговые напряжения поперек направления субдукции Русской палеоплиты отсутствуют. Оставшиеся уравнения, в пренебрежении малым W = ( Z ² x V / в ), приводят к следующему условию для y и а :

{( A ² x x ) + [ x² x ( y + k x² x x )] - D 2 - {[( x ² x k x² ) / [( x² x k x² ) + A ²]² } x [( ax p xgxx ³ xT ') / n > ] + [(4 xy 7 xBxD 1 xA² /x )]} ² + {[ x²x( a - ( kx x U) ] + [( x ² xk x ) x [( x ² xk x ²)- A ²] x ( BxT' + ax p xgxD 1 )] / [( x ² x k x ²) + A ²] ² } ² = 0,     (17)

где B = Z x U' / T , D 1 = 4 x x x [ D - (^) x C x tg в ] / ( p xc p ), D 2 = 4 x n x Z x [ D - (^) xCx tg в ] ² / ( p xc_pxT) , и, согласно формуле (5),

T ’ = [( T max - T_m ) / tg в ] = [( П x V ²) / ( k x tg в )] x (1 / { F + [( x x V x G ) / x ]}). (18)

Из условия (17), эквивалентного двум независимым уравнениям, получаем t = tg в : Y l = Y ( k y = 0) = 4 x n x Z x [( D - Cxt / 2) ² / ( x ² x p xc p xT) ] + {( p x a xgxx ³ xT 'xk ² x ) / n j x [( x ² x k ² x )+ A ²] ² } + 16 x n x { U'xk ² x x A² x Z x [( D - Cx t / 2)/

[( x ² x k x ²)+ A ²] ² x p xc p xT) ]} - { x x [( x ² x k ² x )+ A ²] / x ² },                                                (19)

a = a ( k y =0) = k x xU - {[ k x x ( x ² xk x ² - x ² )] / [ x ² xk x ² + X ² ) ² ]} x {[( T'xU'x Z ) / T ] + 4 x [ p x a x g x x x ( D - Cx t / 2) / p x c p ]},                      (20)

где a = 3 x 10^-5 1/ К - коэффициент теплового расширения, g - ускорение силы тяжести, T ' = ( T max - T m ) / t , t = tg в , Z = ( E* + pxV* ) / ( RxT) , E* и V* - энергия и объем активации, R - универсальная газовая постоянная, U' = {[ D x (sin в x cos в + в )] - [ C x (sin ² в )]} / tg в , Л² = X² + 4 x^, A = [ п / (tg в )], C = - Vx {[ в x sin в ] / [ в ² - sin ² в ]} , D = V x {[(fl x cos в) - Sin в ] / [ в 2 - Sin ² в ]} , T = (T max + T m ) / 2.

В формуле (19) зависимость от средней вязкости n c возникает из-за существенной вблизи желоба термической неустойчивости, описываемой первым слагаемым в (19) и связанной с экспоненциальной зависимостью вязкости от Z , т.е. от температуры.

Из формул (19)-(20) видно, что в полученном первом приближении, которым мы ограничимся, инкремент y и частота а являются функциями горизонтальной координаты x и, таким образом, должны быть плавно меняющимися функциями, что естественно при малых углах (в ) наклона зоны суб-дукции. Благодаря присутствию воды в мантийном клине вязкость его материала может быть очень мала (Жарков, 2012), рс = 3 x 1018 Пас и менее. Примем величину kx - волнового числа - такой, что пространственный период [(2 x п)/kx ], разделяющий соседние восходящие конвективные потоки в мантийном клине, равен среднему наблюдаемому расстоянию между соседними геологотектоническими зонами, параллельными Уральскому палевулканическому хребту, изображенными на рис. 1 косой штриховкой (Порфирьев, 1982), т.е. [(2 x п) / kx ] = 300 км. Считая Z = 20, что соответствует энергии активации E* = 240 кДж/моль и активационному объему V* = 8 см3/моль (Жарков, 2012), угол поддвигания в ~ 10° субдуктирующей литосферы Русской палеоплиты под литосферу Уральского палеоокеана (ЗападноСибирскую плиту) (литосферные плиты в восточном направлении субдуктируют полого, например, плита Наска под углом 20 -30° (Barazangi et al., 1976)) и подставляя приведенные выше значения других параметров, входящих в (19), находим распределения γ как функции x при различных скоростях субдукции, показанные на рис. 5. Видно, что инкремент γ положителен (т.е. конвекция может проявляться) при V > 5 см/год, а при V ~ 6 см/год конвектирущая зона занимает диапазон расстояний (x2 – x1) ~103 км от горного пояса. Эта величина хорошо согласуется со средней широтной протяженностью геолого-тектонических зон Западной Сибири (рис. 1) и, следовательно, дает оценку скорости палеосубдукции в области восточнее Уральского палеовулканического пояса (со -временный Уральский хребет). Эта оценка практически не зависит от принятой средней вязкости ηc , поскольку движущий конвекцию перепад температуры (Tmax – Tm), со -гласно формуле (5), пропорционален ηc , но, с другой стороны, чем больше ηc , тем труднее возбудить конвекцию. Это видно из формулы (19), где три последних слагаемых, описывающих конвекцию, очень слабо или вообще не зависят от ηc , а первое слагаемое, описывающее термическую неустойчивость, мало при ηc < 3×1018 Па.с.

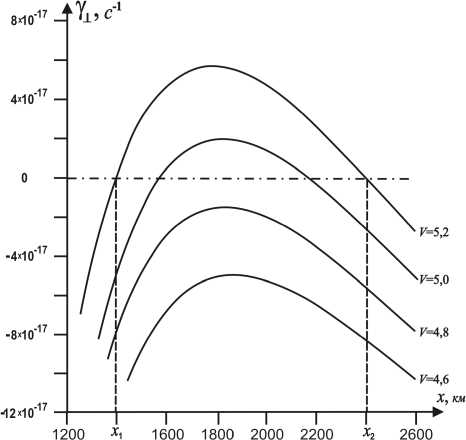
Рис. 5. Инкременты γ конвективной неустойчивости в субдукционном мантийном клине как функции горизонтального расстояния x (в км) от Уральского палеовулканического пояса при различных скоростях V (в см/год) палеосубдук-ции. В интервале x 1 < x < x 2 положительных γ можно ожидать скорость конвективного потока нагретого вещества в мантийном клине Русской палеоплиты V ~ 6 см/год

Обсуждение результатов исследований

Изложенная методика может представлять некоторый интерес для геофизиков, занимающихся изучением глубинного строения мантии в зонах субдукции, т.к. развивает определенный подход к геодинамике в зонах субдукции. В этой статье о бсуждаются две основные темы: поток в мантийном клине и конвективная неустойчивость в нем. Выдвинутая нами идея о том, что потоком за счет вязкости генерируется достаточно тепла, может быть обоснована следующим образом. В частности, нужно отметить, что вопрос о прогреве холодного субдуцирующего блока в нашей работе не затрагивается. Он в принципе уже решен в статье McKenzie (1969). Именно субдуцирующий блок прогревается кондуктивной теплопроводностью из вмещающей мантии и к глубине 700 км практически полностью размягчается. Мы также учитывали дополнительный диссипативный нагрев в мантийном клине, где максимум температуры достигается вблизи верхней грани субдуцирующей плиты, над верхней гранью. Без учета конвекции в мантийном клине этот дополнительный нагрев, по сравнению с работой (McKenzie, 1969), несколько сильнее бы прогревал субдуцирующий блок, но благодаря конвекции диссипативное тепло уносится вверх (там, где инкремент конвективной неустойчивости положителен, т.е. где конвекция действительно развивается). При угле поддвигания β субдуцирующе-го блока Русской палеоплиты порядка 10° горизонтальная протяженность области, где еще возможна конвекция, составляет немного более 1000 км при скорости около 5 см / год .

Кроме того, выделенная нами система субпараллельных структур на территории Западно -Сибирской плиты объясняется как действие конвективных вихревых структур мантии вокруг зоны субдукции. Безусловно, могут быть и некоторые другие предположения на этот счет. Приведем краткую сводку публикаций на эту тему: McKenzie, 1969; Schubert, Turcotte, Olson, 2001; Turcotte, 2002; Karig, 1971. Однако подтверждением изложенного нами механизма взаимодействия конвективных мантийных вихрей, про - явившихся в приповерхностных геологических структурах, является то, что подобные структуры были обнаружены и в других районах субдукции Мирового океана (Karig, 1971).

Заключение

Таким образом, можно считать, что скорость палеосубдукции Русской палеоплиты с учетом расстояния до Уральского палеовул-канического пояса может быть заметно ниже полученного значения V ~ 5 – 6 см/год только при угле субдукции в << 10°. Мы попытались сравнить полученные результаты расчетов с независимыми данными глубинных геофизических разрезов (Петров и др., 2001; Павленкова и др., 2014), пересекающих Уральский хребет и Западную Сибирь, чтобы выяснить полученный ими угол наклона погружения (палеосубдукции) Русской плиты. Результаты таких исследований приведены на рис. 6 (Павленкова, 2014).

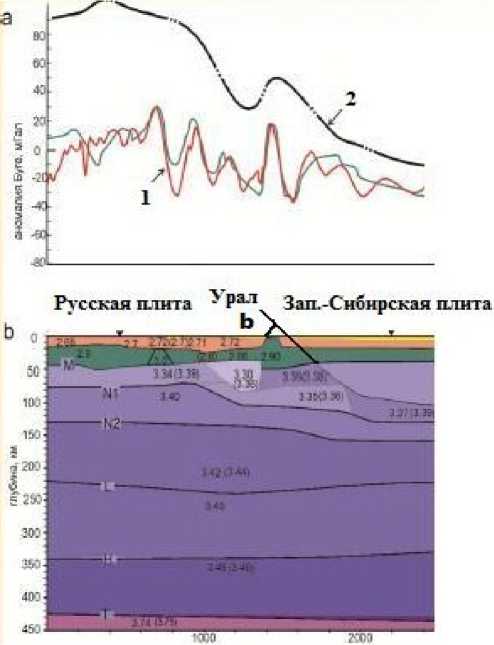
Рис. 6. Фрагмент глубинного геофизического разреза (по сейсмическим и гравитационным данным) по профилю «Кварц» в зоне сочленения Русской и Западно-Сибирской плит (Павленкова и др., 2014), показывающий: а – кривые измерен- ного и расчетного гравитационного поля, представленного в редукции Буге: 1 – (кривая коричневого цвета) – наземные измерения гравитационного поля вдоль профиля «Кварц» ; 1 – (кривая серого цвета) – результаты решения прямой задачи гравиразведки по профилю «Кварц»; 2 – (кривая черного цвета) – результаты расчета сглаженного гравитационного поля по профилю «Кварц», по данным альтиметрических аномалий, измеренных на космических аппаратах. б – глубинный разрез по профилю «Кварц», на котором видно наклонное погружение литосферного слоя Русской плиты (между нижней границей земной коры (М) – Мохоровичича и границей (N1) литосферы) под Западно-Сибирскую плиту, трактуемое как остаточные фрагменты па-леомантийного клина, возникшего при палеосуб-дукционном погружении Русской палеоплиты под Восточно-Сибирскую в районе зоны расположения Уральского палеоокеана в палеозойский период эволюции Земли. На глубинном разрезе цифрами обозначена плотность горных пород (г/см3) различных слоев земной коры и верхней мантии: M – граница Мохоровичича, являющаяся нижней границей («подошвой») земной коры; граница N1 литосферного слоя мантии; граница N2 астеносферного слоя мантии; L, H, T – другие более глубокие границы слоев разного плотностного состава верхней мантии. На данном геофизическом разрезе вертикальный и горизонтальный масштабы разные и поэтому при рассмотрении статьи необходимо ввести некоторый коэффициент пропорциональности, позволяющий из угла (b), изображенного на рисунке, вычислить истинный угол наклона (ft) Русской плиты в настоящий геологический период эволюции Земли. Истинный угол наклона (в) Русской плиты под Западно-Сибирскую в настоящее время составляет около 8ºС по данным наших расчетов с учетом косинусоидальной поправки за неортогональность направления профиля «Кварц» к линии простирания гребня Уральского хребта

Из рис. 6 хорошо видно, что экспериментально определенный по геофизическим (сейсмическим, гравитационным) данным угол наклона современной литосферы Русской плиты (слой между границей Мохоровичича – М и границей – N1 ) составляет в среднем не более 10°, что может свидетельствовать в пользу правильности проведенных в статье расчетов угла наклона пале-осубдукционной зоны Русской палеоплиты. Этот разрез палеосубдукционной зоны (рис.

• 6)    по структуре гравитационного поля очень похож на разрез современной Тихоокеанской субдукционной зоны в районе Охотского моря, приведенный на рис. 3 (кривая 2). Конечно, за многие миллионы лет, прошедшие с палеозойского периода активизации пале-осубдукционной зоны в зоне коллизии Русской и Восточно-Сибирской палеоплит, произошли определенные геолого-тектонические изменения в переходной зоне сочленения этих палеоплит, на территории Западно-Сибирской плиты (древняя территория, называвшаяся Уральским палеоокеаном), но тем не менее многие специалисты в области геологии считают, что на этом геофизическом разрезе (Павленкова и др., 2014) можно видеть остаточные фрагменты палеозойского палеосубдукционного погружения Русской палеоплиты. Кроме того, частота ю , согласно формуле (20), привязана к средней горизонтальной скорости U c = ( D * в } — { C* [(1 - в) / tg в ]} = 0 в мантийном клине, и при малых углах наклона в зоны субдукции выполняется условие ( у >>  ю ). Это означает, что конвективные вихри Карига в целом мало смещаются в горизонтальном направлении: ( ю / k x ) <  2x10 ’2 см/год . Изложенная методика может помочь при проведении региональных поисковых и разведочных работ на углеводороды в аналогичных районах в окрестности расположения субдукционных и палеосубдукционных зон Земли.

Выводы

• 1.    Конвективная зона, состоящая из трех пар конвективных вихрей Карига, в пале-осубдукционном мантийном клине занимает диапазон расстояний около тысячи километров от Уральского палеовулканического пояса. Эта величина хорошо согласуется со средней широтной протяженностью трех геолого-тектонических зон Западной Сибири (около 300 км каждая), следовательно, дает возможность сделать оценку скорости палеосубдукции в области к востоку от Уральской палеовулканической дуги (современный Уральский хребет).

• 2.    Конвективные вихри Карига, поскольку их может быть несколько при достаточно пологой зоне субдукции, располагают-

• 3.    Скорость палеосубдукции Русской палеоплиты в палеозойский период эволюции Земли с учетом расстояния до Уральского па-леовулканического пояса может быть заметно ниже полученного значения V ~ 5 – 6 см/год только при угле субдукции в <<  10°.

ся в мантии над субдуцирующим блоком и под надстилающей литосферой. Иными словами, вихри Карига обычно расположены в мантийном клине, в нашем случае, при погружении (палеосубдукции) Русской палеоплиты, они были расположены к востоку от Уральского палеовулканического пояса на расстоянии 300 км друг от друга.