Геомагнитный метод автоматической диагностики границ авроральных овалов в двух полушариях Земли

наблюдаемых дискретных и диффузных полярных сияний, создаваемых потоками энергичных электронов и протонов, непрерывно высыпающихся из магнитосферы и многократно усиливающихся в пери- оды магнитосферных суббурь и бурь. Высокоширотная граница аврорального овала (АО) соответствует границе полярной шапки (ПШ, границе закрытых и открытых геомагнитных силовых линий), а низкоширотная граница АО — плазмопаузе и внутренней кромке плазменного слоя. По сложившимся представлениям о физике и топологии магнитосферы Земли ночные области АО и ПШ в двух полушариях представляют собой сопряженные ионосферные проекции плазменного слоя, содержащего плотную плазму на закрытых силовых линиях, и двух очень протяженных долей магнитосферного хвоста с разреженной плазмой и открытыми (или сильно вытянутыми) в солнечный ветер силовыми линиями [Akasofu, 1977; Feldstein, Galperin, 1985; Heikkila, 2011]. Крупномасштабная структура (формы, границы и размеры) долей хвоста и плазменного слоя определяется квазистационарными физическими процессами переноса массы, импульса и энергии из солнечного ветра в магнитосферу, а также взрывными процессами высвобождения накопленной магнитной энергии хвоста во время суббурь. Исследование пространственно-временной динамики границ АО в сопряженных ионосферах, формы и положения ПШ и величины открытого магнитного потока через них в спокойных и возмущенных геомагнитных условиях — давняя, но по-прежнему актуальная научная задача физики магнитосферы и магнитосферных суббурь [Akasofu, 1977, 2013; Shukhtina et al., 2016], в рамках решения которой выполнена и настоящая работа.

Планетарная морфология и динамика полярных сияний исследуются с помощью целого ряда наземных (фото- и киносъемка, фотометрия и спектроскопия, радары) и спутниковых (детекторы частиц, фотосъемка и фотометрия) средств и методов [Jones, 1974]. Полвека назад на основе анализа большого объема фотографий полярных сияний, полученных камерами всего неба на мировой сети наземных обсерваторий, была сформулирована концепция АО [Feldstein, 1964; Хорошева, 1967; Акасофу, 1971] и получены первые статистические модели АО для разных уровней геомагнитной активности [Feldstein et al., 1968]. В современных исследованиях полярной ионосферы широко применяются три спутниковых метода наблюдений АО и определения его границ. В первом методе используются локальные (вдоль траектории спутника) измерения параметров энергетического спектра высыпающихся магнитосферных электронов и протонов, а границы АО находятся по резким градиентам этих параметров. Пролеты одного спутника над определенной географической точкой разделены интервалом ~100 мин, поэтому этот локальный метод не дает мгновенной пространственной структуры границ АО даже вдоль одной траектории. Однако большой объем многолетних спутниковых данных известного проекта DMSP позволил создать информативные статистические модели границ АО, такие как зарубежная OVATION [Newell et al., 2014] и отечественная APM [Vorobjev et al., 2013]. Второй метод обеспечивает глобальную диагностику АО с шагом ~2 мин на основе его фотосъемки в ультрафиолете камерами широкого обзора со спутников с полярными орби- тами (проект IMAGE & Polar) [Boakes et al., 2008; Longden et al., 2010]. Недостатками данного метода являются зачастую неполный охват фотокамерой АО и ПШ, а также сильная «засветка» солнечным ультрафиолетом дневной части АО [Milan et al., 2009]. Кроме того, для обеспечения непрерывной и одновременной глобальной диагностики АО в обоих полушариях необходимо постоянное функционирование как минимум двух дорогостоящих полярных спутников. В последние годы активно развивается третий спутниковый метод диагностики границ АО по двумерным картам распределений плотности крупномасштабных продольных токов (ПТ) в рамках крупного проекта AMPERE. В этом проекте группировка из нескольких десятков спутников обеспечивает непрерывный расчет таких карт ПТ в двух полушариях с временным разрешением ~10 мин [Coxon et al., 2018; Burrell et al., 2020]. Очевидно, что создание новых методов диагностики АО с лучшим пространственно-временным разрешением необходимо как альтернатива и/или дополнение к существующим средствам и способам для более полного понимания физических процессов в системе солнечный ветер — магнитосфера — ионосфера и решения актуальной научной проблемы магнитосферных суббурь.

В данной статье мы продолжаем разработку нового наземного геомагнитного метода автоматической диагностики границ АО по выходным данным техники инверсии магнитограмм (ТИМ), основы которого заложены нами в [Кондратьев и др., 2017; Лунюшкин, Пенских, 2019] . Основные цели и задачи настоящей работы: развитие геомагнитного метода для одновременной диагностики границ АО в двух полушариях; тестирование точности метода по схеме «ручной/автоматический»; сравнение полученных геомагнитным методом границ АО с данными прямых наблюдений АО со спутника IMAGE и результатами моделей SuperDARN, OVATION, APM.

АЛГОРИТМГЕОМАГНИТНОГО МЕТОДА

В основе развиваемого наземного геомагнитного метода автоматической диагностики границ авроральных овалов в двух полушариях Земли лежит отечественная ТИМ, созданная в ИСЗФ СО РАН [Базаржапов и др., 1979; Mishin, 1990; Ширапов, Мишин, 2009]. ТИМ обеспечивает расчет двумерных распределений эквивалентных токов, электрического потенциала, горизонтальных и продольных токов и других электродинамических параметров высокоширотной ионосферы на основе одноминутных данных геомагнитных измерений на мировой сети наземных станций. В последние годы программный комплекс ТИМ был существенно модернизирован и полностью адаптирован для научно-исследовательской работы на основе единой базы цифровых геомагнитных данных, созданной в масштабном проекте SuperMAG [Gjerloev, 2012]. Открытый доступ к этой базе, содержащей богатый ежегодно обновляемый архив, дает сайт [].

Физические положения, теория и базовый алгоритм геомагнитного метода диагностики границ АО подробно изложены нами в статье [Лунюшкин, Пенских, 2019] . Ниже мы кратко опишем только основные из них.

Метод использует крупномасштабные пространственные распределения эквивалентной токовой функции J (θ, λ) и плотности ПТ i || (θ, λ), рассчитываемые на первом этапе ТИМ в приближении радиального геомагнитного поля и однородной проводимости ионосферы:

J = T ^ H U + J 0 , (1)

i||=-ΣP ∆J, (2) ΣH где в первом члене (1) верхний знак (минус) соответствует Северному полушарию, а нижний (плюс) — Южному; J0 — калибровочная константа; U=U(θ, λ) — распределение ионосферного электрического потенциала; θ — геомагнитная коширота; λ — местное геомагнитное время; Δ — оператор Лапласа; ΣP, ΣH — интегральные ионосферные проводимости Педерсена и Холла, заданные константами ΣH = 10 См и ΣP/ΣH = 1; формула (2) одинакова в обоих полушариях.

Из (1) следует выражение A J = t^_h A U, подстановка которого в (2) устанавливает связь плотности ПТ i || с электростатическим потенциалом U :

i _|| = ±Σ _P ∆ U . (3)

Подстановка уравнения Пуассона ∆ U =- ρ/(εε₀) в (3) показывает связь i || с электрическими зарядами, переносящими ПТ и потенциал U от магнитосферных генераторов ЭДС в ионосферу.

Формула (1) позволяет работать с токовой функцией J как с электрическим потенциалом U , а с градиентом J — как с создающим ионосферную конвекцию электрическим полем E :

V J = T S _H V U = ±S_h E . (4)

На основе элементарных физических формул (1)–(4) построен алгоритм диагностики границы обращения магнитосферно-ионосферной конвекции (RB) — важнейшего физического параметра, контролирующего перенос массы и энергии из солнечного ветра в магнитосферу через мантию открытых долей хвоста и низкоширотный пограничный слой. Граница RB непременно проходит через два главных фокуса токовой функции J, соответствующих утреннему и вечернему экстремумам в распределении потенциала U, а также совпадает с линией максимума плотности ПТ зоны 1, передающих в ионосферу электрический потенциал U от основного генератора солнечный ветер — магнитосфера. В нашем методе реализованы два способа определения границы RB: по эквивалентной токовой функции J, где граница RB проходит по точкам с минимумами ∇J; на основе распределения плотности ПТ — здесь граница RB проводится по линии максимумов плотности ПТ зоны 1. Два способа могут использоваться как совместно, так и самостоятельно — например, при определении границы RB по моделям электрического потенциала (SuperDARN и др.) и/или ПТ (AMPERE и др.).

Рисунок 1 на примере одного из моментов суббури 27.08.2001 иллюстрирует вышеизложенные способы проведения границ RB на картах токовой функции (слева) и ПТ (справа). Здесь и на всех аналогичных рисунках красный цвет изолиний соответствует положительному значению функции, синий — отрицательному. В [Лунюшкин, Пенских, 2019] нами было показано теоретически, что два способа взаимосвязаны и должны давать совпадающие результаты (с погрешностью, определяемой шагом расчетной сетки по широте), что подтвердилось и тогда, и в ходе всей дальнейшей работы. Смысл других границ АО (R0, R1, R2, RH), указанных на рис. 1, разъясняется в следующем параграфе.

Магнитная сопряженность АО двух полушарий с плазменным слоем, отмеченная во введении, обеспечивается также электродинамической взаимосвязью системы магнитосфера — ионосфера посредством крупномасштабных ПТ зон 1 и 2 Ииджимы — Потемры [Iijima, Potemra, 1978] , текущих вдоль геомагнитных силовых трубок сопряженных областей. Пространственное соответствие зон 1, 2 ПТ и АО подтверждено многими исследованиями [Coley, 1983; Fujii et al., 1990; Gary et al., 1998; Korth et al., 2014; Carter et al., 2016; Xiong et al., 2020] . Исходя из этой сопряженности, в постоянную практику ТИМ давно внедрена визуально-ручная методика определения границ АО по картам распределений крупномасштабных ПТ [Mishin et al., 1986, 1992] . Полярная граница АО (или граница ПШ, обозначаемая нами как R0) определяется по высокоширотной границе зоны 1 ПТ (см. рис. 1 справа), а экваториальная граница АО (R2) — по низкоширотной границе зоны 2 ПТ. Находится также граница раздела зон 1 и 2 ПТ (R1), соответствующая широтным максимумам интенсивностей западной и восточной авроральных электроструй, дополнительно определяется линия максимумов плотности ПТ зоны 2 (RH). Здесь необходимо пояснить, что в принятых нами обозначениях для диагностируемых границ АО (R0, RB, R1, RH и R2) буква R (Radius) имеет смысл радиус-вектора, измеряемого от полюса в градусах кошироты полярной системы координат, используемой в ТИМ. Радиусы R0, R1 и R2, соответствующие южным границам ПТ зон 0, 1 и 2, не следует путать с похожими обозначениями R0, R1 и R2, часто применяемыми в литературе для трех зон ПТ Ииджимы—Потемры, где буква R (Region) означает зону/область.

Давняя и актуальная методическая задача программного комплекса ТИМ — создание автоматического метода определения границ АО взамен трудоемкого визуально-ручного способа. Эта задача в основном была нами решена [Лунюшкин, Пенских, 2019] , настоящая работа развивает наземный геомагнитный метод диагностики границ АО, в том числе — на Южное полушарие. Ниже дается описание

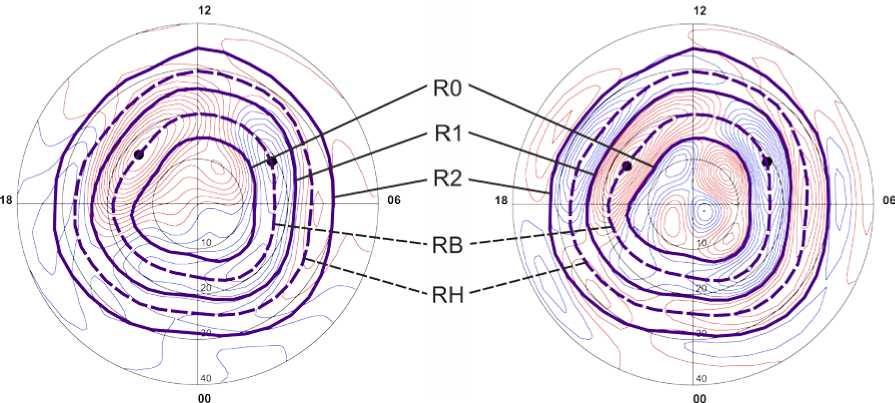
Рис. 1 . Эквивалентная токовая функция (слева) и плотность ПТ (справа) с однородной проводимостью в Северном полушарии для 03:55 UT 27.08.2001: R0 — граница полярной шапки; RB — граница обращения конвекции (линия максимума плотности ПТ зоны 1); R1 — граница между зонами 1 и 2 ПТ; RH — линия максимума плотности ПТ зоны 2; R2 — экваториальная граница АО; жирные точки — основные фокусы

алгоритмов реализации геомагнитного метода с некоторыми уточнениями, дополнениями и модификациями.

Поиск основных фокусов

Граница R1 разделяет области втекающих и вытекающих ПТ зон 1 и 2 внутри АО, а граница R0 — ПТ зоны 1 и ПТ зоны 0 в ПШ (рис. 1). Очевидно, что чем больше амплитуда изменения значений плотности ПТ до и после границы ПТ, тем резче эта граница между ними и тем проще ее определение. Ясно также, что наибольшая амплитуда изменений будет иметь место на меридиане с минимумом/максимумом плотности ПТ. В районе двух главных фокусов ПТ зоны 1, как правило, хорошо выражены и границы зон ПТ. В районе двух главных фокусов токовой функции J обычно четко видна граница обращения ионосферной конвекции RB. Указанные минимумы и максимумы функции J (как аналога электрического потенциала) располагаются, согласно теории и наблюдениям, вблизи меридиана утро–вечер [Heppner, 1972; Lu et al., 1989] .

В начале данного раздела мы особо отметили, что граница обращения ионосферной конвекции RB непременно проходит как по утреннему и вечернему фокусам токовой функции J , так и по соответствующим основным фокусам плотности ПТ зоны 1, т. е. координаты основных фокусов функции J и ПТ зоны 1 практически одинаковы. Зачастую на практике как на токовой функции, так и на картах ПТ зоны 1, наблюдается не по два, а по три и более фокусов. Таким образом, возникает задача выбора двух основных фокусов.

Основные фокусы как для токовой функции J, так и для плотности ПТ зоны 1, должны иметь наибольшие значения, а не оказаться небольшими локальными экстремумами. Кроме того, координаты основных фокусов функции J и основных фокусов ПТ зоны 1 должны быть примерно одинаковыми. Таким образом, можно сформулировать критерий выбора основных фокусов из всех возможных кандидатов. Чем больше значение в фокусе функции J, тем больше значение в фокусе ПТ, и чем меньше расстояние между этими фокусами, тем больше весовой коэффициент knm = i||nJm                                             (5)

dnm где i||n — значение плотности ПТ в n-м фокусе; Jm — значение эквивалентной токовой функции в m-м фокусе; dnm — расстояние (ортодрома) между фокусами плотности ПТ и фокусами функции J; knm — весовой коэффициент для пары n-го и m-го фокусов.

Согласно формулам (1), (2), в зоне 1 значения плотности ПТ имеют те же знаки, что и токовая функция J . Поэтому знак модуля в формуле (5) не требуется, следовательно, коэффициенты для фокусов зоны 1 ПТ будут положительными. При расчете весовых коэффициентов проводится предварительная нормировка плотности ПТ и функции J в диапазоне [–1; 1], поскольку они имеют различный порядок величин. В результате, рассчитав весовые коэффициенты по формуле (5), выбираем два основных фокуса с максимальными коэффициентами: один — для утреннего сектора ионосферы, другой — для вечернего.

Поиск границ вдоль основного меридиана

Каждый из найденных основных фокусов имеет свою кошироту и долготу (основной меридиан). Двигаясь от фокуса вдоль основного меридиана к экватору и к полюсу, определяем границы АО, описанные в начале данного раздела и указанные на рис. 1:

RB — совпадает с положением фокуса;

R1 — первая смена знака (к экватору);

RH — первый экстремум (к экватору);

R0 — первая смена знака | первый экстремум | полузона (к полюсу);

R2 — первая смена знака | первый экстремум | полузона (к экватору);

| — знак операции, обозначающий «если не найдено, то».

Найти границы R0 и R2 на практике бывает сложнее, чем другие границы. Если смена знака не найдена, используем экстремум как опорную точку. Однако и это не всегда помогает. В таком случае можно определить R0 и R2 через полузоны ПТ. Полагая из опыта, что RB делит зону 1 ПТ примерно пополам, можно рассчитать кошироту R0: R0=RB–(R1–RB). Аналогично, полагая, что RH делит зону 2 ПТ пополам, получаем: R2=RH+ (RH–R1).

Поиск границ-кандидатов на соседних меридианах

Найденные границы в районе двух основных фокусов являются двумя сегментами искомых полных границ. На первом этапе эти сегменты границ соответствуют своему основному меридиану. Каждый найденный сегмент границ имеет по два соседних меридиана. Находим границы на этих соседних меридианах. Полагая, что граница RB на текущем меридиане не должна значительно отклоняться от границы на предыдущем меридиане, находим ее кошироту как ближайший экстремум к кошироте границы RB предыдущего меридиана. Остальные границы-кандидаты для R1, RH, R0, R2 на соседних меридианах определяются аналогичным образом.

Выбор дальнейшего наилучшего меридиана

Как правило, на соседних меридианах граница резко не меняется. В полярной системе координат это свойство можно выразить по аналогии с тангенсом угла наклона α tg α=

θ p -θ c λ _p -λ

где θ p , θ c — кошироты на предыдущем и текущем меридиане соответственно; λ_p, λ_c — долготы на предыдущем и текущем меридиане соответственно.

Существуют места, где граница легко определяется и нет большого изменения в коширотах между текущим и предыдущим меридианами. Как правило, в таких местах граница определена корректно. Таким образом, из четырех меридианов с кандидатами-границами можно выбрать один меридиан, границы на котором будут образовывать наименьший перепад, рассчитанный по формуле (6). Поскольку одновременно проводится несколько границ, необходимо рассчитывать средне-арифметический тангенс для всех границ соседних меридианов и из них выбирать меридиан с наименьшим тангенсом.

Два сегмента границы (утренний и вечерний) должны соединиться друг с другом в единую замкнутую границу. Поэтому критерий минимального тангенса используется не только для соседних меридианов, но и для соединения сегментов границ.

В результате итерационного выполнения данного пункта получаем утренний и вечерний сегменты границ R0, RB, R1, RH, R2, которые затем соединяются друг с другом. Если сегменты не соединились из-за сложности проведения границ в районе дневного и ночного разрывов Харанга, проводим интерполяцию границы. После трехточечного сглаживания получаем окончательные границы R0, RB, R1, RH, R2 аврорального овала.

Ход изложенного решения показан на рис. 2.

Поиск ночного и дневного разрывов Харанга

Граница между положительной и отрицательной бухтами в горизонтальной компоненте H возмущения наземного геомагнитного поля в ночной авроральной зоне была впервые обнаружена Harang [1946] . Такое обращение вектора H связано с переходом из области восточной электроструи (Δ Н >0) в область западной (Δ Н <0). Поскольку электроструи являются в основном ионосферными токами Холла, соответствующий поворот наблюдался также и в распределениях электрического поля [Maynard, 1974] . Из аналогии эквивалентной токовой функции J и электрического потенциала U , описываемой формулой (4), в Северном полушарии имеем ∇ J = -Σ _H ∇ U , т. е. ∇ _θ,λ J =Σ _H E _θ,λ . Следовательно, повороту электрического поля E _N → E _W → E _S соответствует изменение градиента токовой функции ( ∇ _θ J < 0) → ( ∇ _λ J < 0) → ( ∇ _θ J > 0). Это означает, что в секторе ночного Харанга восточный эквивалентный ток поворачивает против часовой стрелки и переходит в западный ток [Untiedt, Baumjohann, 1993] . Аналогичная, но обратная ситуация имеет место в области дневной «встречи» авроральных электроструй.

Учитывая вышеизложенное, в алгоритме геомагнитного метода положения ночного и дневного разрывов Харанга находятся по изменениям знака ∇ _θ J на границе R1, вдоль которой текут восточная и западная авроральные электроструи.

Южное полушарие

Описанный выше алгоритм геомагнитного метода автоматической диагностики границ R0, RB, R1, RH и R2 аврорального овала вначале был создан нами для Северного полушария [Кондратьев и др., 2017; Лунюшкин, Пенских, 2019] . Расширение метода ТИМ на Южное полушарие [Lunyushkin et al., 2019] стало возможным на основе современной цифровой базы наземных геомагнитных данных SuperMAG [Gjerloev, 2012] и дополнительно проведенных исследований по методу наибольших вкладов — основному методу решения системы уравнений ТИМ [Пенских, 2020] . Все это позволило реализовать геомагнитный метод диагностики границ АО в Южном полушарии.

В данной работе Южное полушарие на всех рисунках представлено в виде «сквозь Землю», общепринятом в современной литературе. Для удобства

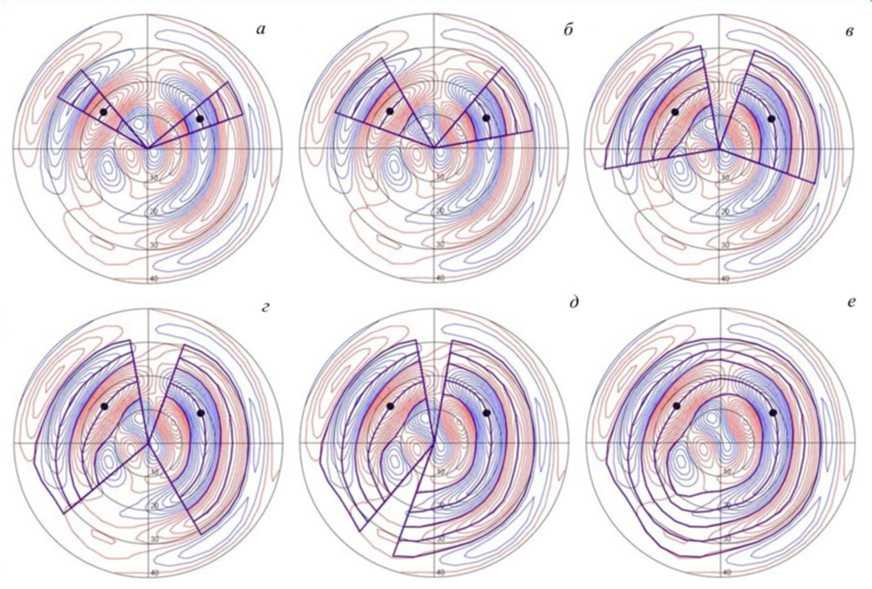
Рис. 2 . Последовательность ( а – е ) работы алгоритма при построении границ АО по распределениям плотности ПТ на примере момента 03:50 UT 27.08.2001

межполушарного сравнения кошироты Северного и Южного полушарий, а соответственно и кошироты всех границ АО, отсчитываются от своего соответствующего дипольного полюса.

ТЕСТИРОВАНИЕ ГЕОМАГНИТНОГО МЕТОДА

Для оценки общего уровня геомагнитной активности в авроральных широтах используют, как правило, AE -индекс, по которому в большинстве исследований проводится также таймирование основных фаз магнитной суббури. Однако набирает популярность новый авроральный индекс SME [Newell, Gjerloev, 2011] , который является улучшенным аналогом AE -индекса. SME отличается, во-первых, большим количеством используемых станций для его расчета (до 130 в SME против 12 в AE ), во-вторых, — всесторонне продуманной оригинальной методикой определения базисных линий геомагнитного поля на всех наземных магнитных станциях и регулярной очисткой всех первичных геомагнитных данных от обнаруживаемых ошибок различного рода [Gjerloev, 2012] . Использование SME -индекса позволяет, например, намного точнее определить начало взрывной фазы магнитной суббури [Newell, Gjerloev, 2014] .

В данном разделе мы покажем работоспособность автоматического метода определения границ АО в двух полушариях на примере изолированной суббури 27 августа 2001 г., ранее уже детально исследованной [Baker et al., 2005; Mishin et al., 2017]. Это событие выбрано нами также по причине наличия данных одновременных спутниковых наблюде- ний (IMAGE) и подходящих для сравнения выходных данных некоторых моделей (SuperDARN, OVATION, APM). На рис. 3 показаны графики изменения индекса геомагнитной активности в авроральном овале (SME), z-компоненты межпланетного магнитного поля (ММП Bz) и магнитных потоков через северную и южную полярные шапки — параметров, характеризующих развитие суббури 27.08.2001 в интервале 03:00–06:00 UT. Магнитные потоки рассчитывались на высоте 115 км интегрированием дипольного магнитного поля Земли по области на сфере, ограниченной соответствующими границами RB. Для каждой из основных фаз суббури, таймированных в [Mishin et al., 2017], выберем три характерных момента времени (показаны штриховыми линиями на рис. 3) и покажем на этом примере возможности нашего наземного геомагнитного метода автоматической диагностики границ авроральных овалов в двух полушариях Земли по выходным данным ТИМ.

Сравнение автоматического метода с ручным

В первую очередь необходимо корректно оценить работоспособность и точность метода определения границ АО в двух полушариях, исключив при этом возможные погрешности ТИМ. Для этого по каждому полушарию сравним границы АО (R0, RB, R1, RH, R2), построенные автоматическим методом, с границами, определенными вручную. Рисунки 4, 5 показывают, что для трех выбранных моментов времени как в Северном, так и в Южном полушариях, наблюдается хорошее качественное согласие у всех

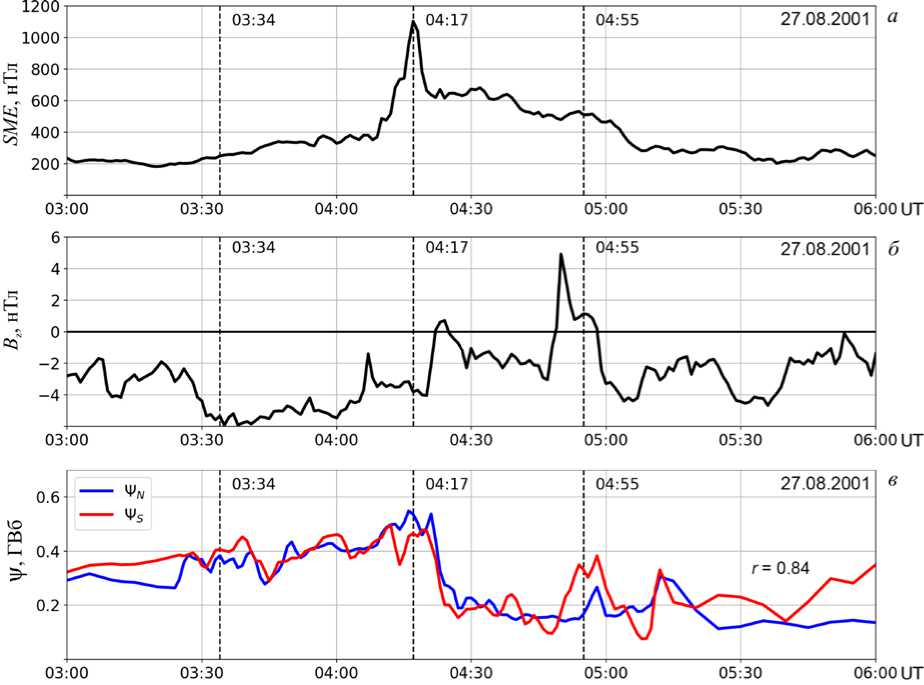
Рис. 3 . Изменение аврорального индекса SME ( а ), ММП B _z ( б ) и магнитных потоков Ψ ( в ) через ПШ Северного (Ψ _N ) и Южного (Ψ _S ) полушарий в ходе суббури 27.08.2001, характерные моменты развития которой отмечены штриховыми линиями: 03:34 UT — фаза роста, 04:17 UT — взрывная фаза, 04:55 UT — фаза восстановления

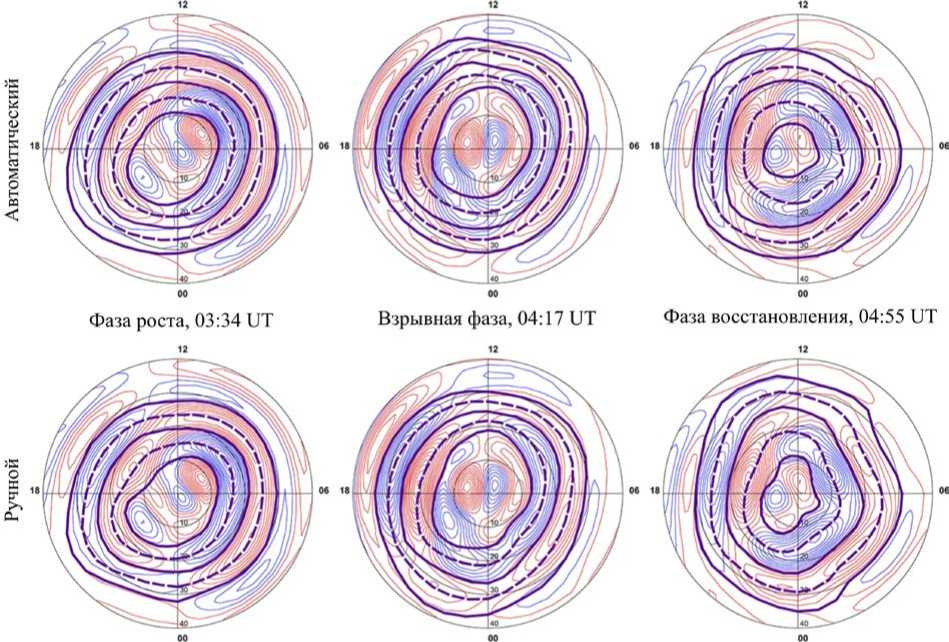
Рис. 4 . Сравнение построенных границ АО для Северного полушария. Верхний ряд — границы, построенные автоматическим методом, нижний ряд — границы, построенные вручную. По столбцам — три характерных момента для трех фаз суббури 27.08.2001

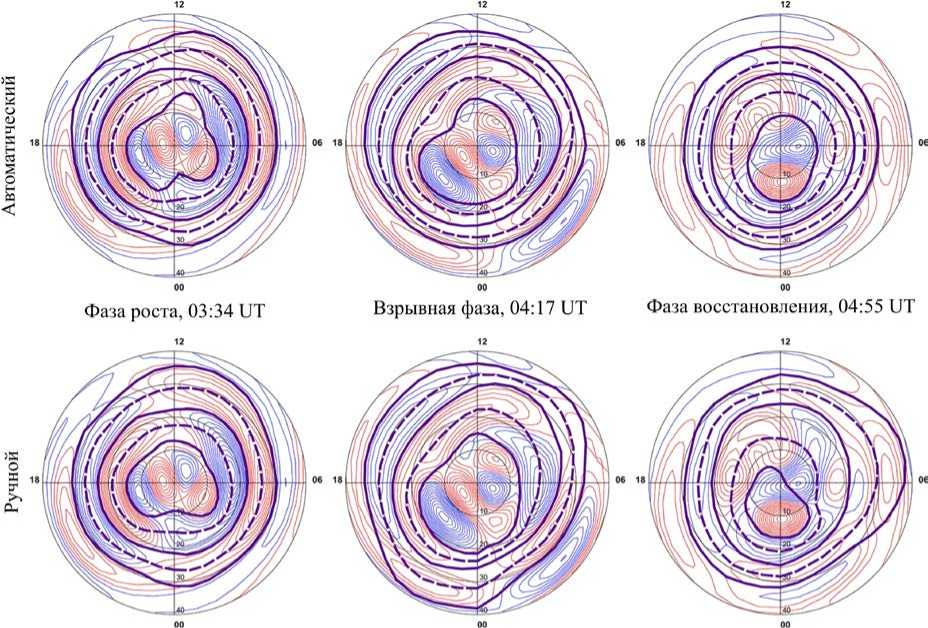
Рис. 5 . То же, что на рис. 4, для Южного полушария

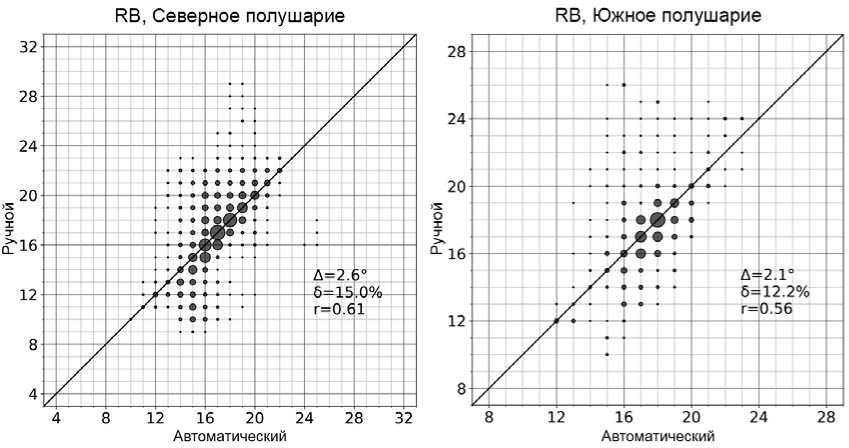
Рис. 6 . Статистическое сравнение автоматического и ручного методов определения границ обращения конвекции RB для суббури 27.08.2001 для Северного (слева) и Южного (справа) полушарий. По осям абсцисс и ординат — кошироты соответствующих границ

соответствующих границ, построенных автоматически и вручную.

Количественная статистическая оценка точности работы автоматического метода диагностики границ АО в двух полушариях показана на рис. 6 на примере границы обращения конвекции RB. При построении графиков для каждого полушария использовались 80 моментов времени, охватывающих трехчасовой интервал выбранной суббури. Для наглядности исходные точки сгруппированы к ближайшему узлу на сетке, диаметр каждой окружности на рисунке про- порционален количеству точек в группе. Графики для других границ АО (R0, R1, RH, R2) имеют схожий с рис. 6 вид для каждого полушария и поэтому здесь не приводятся. Рисунок 6 показывает, что плотности точек лежат преимущественно на главной диагонали рисунка, а среднеквадратичная погрешность составляет ~2° (два шага расчетной сетки по широте в методе ТИМ) при средней корреляции сравниваемых данных.

Стоит отметить, что здесь мы исходили из того, что человек-эксперт абсолютно верно определил

Геомагнитный метод автоматической диагностики границ границы. Однако это не совсем так. Во-первых, в случае повторного проведения границ человек никогда не попадет «точка в точку» и не проведет абсолютно такие же границы, т. е. всегда присутствует какая-то естественная погрешность в силу особенности человеческой руки. Во-вторых, встречаются места, особенно в районе разрывов Харанга, где границы нельзя провести однозначно [Iijima, Potemra, 1978; Coxon et al., 2018; Xiong et al., 2020] .

Сравнение границ аврорального овала с данными других методов

Во введении был отмечен целый ряд наземных и спутниковых средств и методов для наблюдения АО и диагностики его основных границ, в том числе такие крупные проекты, как IMAGE, SuperDARN и OVATION, данные которых мы используем в этом подразделе для сравнения с результатами диагностики границ АО, полученными геомагнитным методом.

Рисунок 7 иллюстрирует результаты сравнения. На второй сверху панели показаны снимки овала полярных сияний в Северном полушарии, полученные со спутника IMAGE для трех выбранных моментов на разных фазах магнитной суббури 27.08.2001. Снимки получены нами с сайта открытого доступа SuperMAG []. На эти снимки наложены границы R0, RB и R2 с верхней панели, где границы АО Северного полушария получены по распределениям ПТ автоматическим геомагнитным методом. В целом можно отметить хорошее качественное соответствие основных границ R0 и R2 аврорального овала, полученных нашим методом, с авроральными сияниями по данным IMAGE для всех трех фаз суббури. Центр овала полярных сияний смещен вправо относительно центра ПТ — это можно объяснить тем, что вытекающий ПТ (высыпающиеся электроны) в вечернем секторе расположен в зоне 1 ПТ в приполярной области АО, а в утреннем секторе — в зоне 2 ПТ, т. е. в приэкваториальной части АО. Третья и четвертая панели рис. 7 показывают аналогичное сравнение границ АО (R0, RB и R2), полученных геомагнитным методом, с изображениями АО, рассчитанными соответственно по модели OVATION-prime [ =typ_redirect] и по модели APM [ /webtool/frontend]. Здесь также следует отметить хорошее качественное согласие наших границ АО с указанными моделями.

На рис. 8 представлены распределения электрических потенциалов в высокоширотной ионосфере по модели SuperDARN-RG96 для Северного и Южного полушарий во время трех фаз магнитной суббури 27.08.2001, на которые наложены границы обращения ионосферной конвекции RB, полученные нашим автоматическим геомагнитным методом. Видно, что в Северном полушарии наблюдается достаточно хорошее качественное соответствие модельного электрического потенциала и границы обращения конвекции по данным ТИМ: граница RB практически проходит по двум основным фокусам электрического потенциала модели RG96. В Южном полушарии, особенно в вечерней области, совпадение нашей границы RB с электрическим потенциалом несколько хуже. Возможно, различие связано с тем, что в период выбранного нами события в Южном полушарии было размещено меньше инструментов, чем в Северном полушарии: 6 против 10 — для радаров SuperDARN [ Radar+ Overview], 30 против 149 — для наземных магнитометров [http://supermag. ]. Хорошо известно, что недостаточно плотная сеть наземных наблюдений существенно влияет на точность решения задач интерполяции как геомагнитных [Rigler et al., 2019], так и радарных измерений [Ruohoniemi, Baker, 1998].

Динамика полярной шапки в ходе изолированной суббури

Во введении отмечалось, что ПШ каждого полушария является ионосферной проекцией соответствующей открытой доли магнитосферного хвоста. Многими исследованиями установлено, что изолированная магнитосферная суббуря хорошо описывается классическим трехфазным циклом Данжи [Akasofu, 1977, 2013; Cowley, Lockwood, 1992; Milan et al., 2007, Akasofu, 2013] . На фазе роста происходит «загрузка» — накопление магнитной энергии в хвосте магнитосферы, что в полярной ионосфере сопровождается увеличением площади ПШ [Russell, McPherron, 1973; Akasofu, 1977; Kamide et al., 1999] . Магнитное пересоединение в околоземной части плазменного слоя [Baker et al., 1996] начинает процесс взрывной фазы суббури, в течение которой и далее на фазе восстановления энергия суббури обеспечивается процессом «разгрузки» накопленной магнитной энергии, который в сопряженной области ионосферы наблюдается как уменьшение площади ПШ [Kamide et al., 1999; Milan et al., 2003, 2007] . Именно такое поведение ПШ — увеличение на фазе роста и уменьшение на фазе восстановления — мы наблюдаем на рис. 4 как для границ R0 и RB в Северном полушарии, определенных как вручную, так и автоматически. Аналогичная картина складывается в Южном полушарии (см. рис. 5), что физически объясняется просто. Во-первых, если магнитосфера рассматривается в приближении сильно вытянутых, но закрытых силовых линий долей хвоста [Heikkila, 2011] , она представляет собой целостную структуру, поэтому увеличение магнитного потока и длины магнитосферного хвоста оказывает равное влияние на северную и южную доли, а следовательно, на их проекции — ПШ в двух полушариях. Во-вторых, в ходе данной изолированной суббури основной вклад в механизм дневного пересоединения [Dungey, 1961; Milan et al., 2007] внесла южная компонента ММП B z , которая, очевидно, в равной степени оказывает влияние на всю магнитосферу, т. е. одинаково «открывает» доли хвоста Северного и Южного полушарий. Такое синхронное изменение долей хвоста двух полушарий подтверждается в границах R0 и динамике магнитных потоков через северную и южную ПШ, полученных с помощью геомагнитного

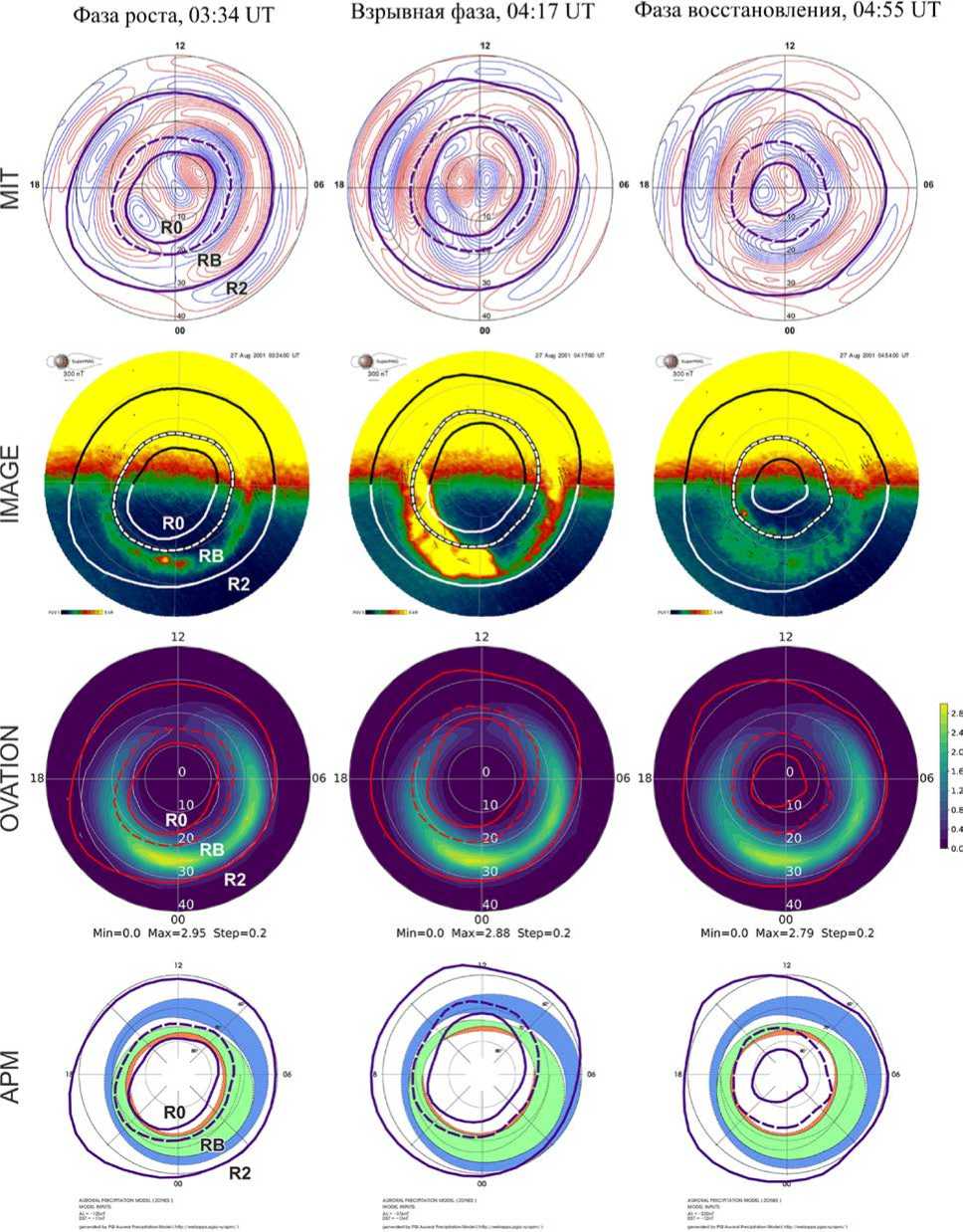
Риc. 7 . Три фазы суббури 27.08.2001 в Северном полушарии. Сравнение границ АО (R0, RB, R2), определенных автоматическим геомагнитным методом по распределениям плотности ПТ ТИМ (MIT) с авроральными сияниями по данным спутника IMAGE и АО по моделям OVATION и APM; границы R0, RB, R2 с верхней панели наложены на нижние панели рисунка

метода (см. рис. 3). Отметим, что синхронная динамика магнитных потоков через ПШ двух полушарий была установлена ручным геомагнитным методом при исследовании магнитной бури 17.08.2001 [Lunyushkin et al., 2019] .

Основная разгрузка накопленной магнитной энергии хвоста происходит во время взрывной фазы магнитосферной суббури [Akasofu, 1977; Mishin et al., 2017] . Изменение площади ПШ во время взрывной фазы не всегда однозначно и зависит от баланса

27/4*^/2001 03:34-03:36 UT

27/4*^/2001 04:16-04:18 UT

27/4*^/2001 04:54-04:56 UT

28      13 О 1       2          3

Фача роста, 03:34 UT

27/4*^/2001 03:34-03:36 ит Th^-torth V*.

22      23 О I 2

Взрывная фаза, 04:17 UT

2 7/4*^/2001 04:16-04:18 ЦТ    Тьги-£»

22      23      0      1        2

Фаза восстановления, 03:34 UT

27/4*^/2001 04:54 -04:56 ЦТ

Рис. 8 . Сравнение границ обращения ионосферной конвекции RB (штриховая толстая линия), определенных геомагнитным методом в Северном (вверху) и Южном (внизу) полушариях для трех фаз суббури 27.08.2001, с соответствующими картами электрического потенциала по модели SuperDARN-RG96

поступающей в магнитосферу энергии и ее высвобождения в энергию авроральных частиц, нагрев ионосферы, в кольцевой ток и др. [Milan et al., 2003, 2007] . Как правило, на взрывной фазе площадь ПШ уменьшается, однако, если B z остается отрицательной, площадь ПШ все еще может незначительно увеличиваться [Kamide et al., 1999] . Именно это и происходило в ходе магнитосферной суббури 27.08.2001 (см. рис. 3–5). Рисунок 9 показывает невысокую межполушарную корреляцию границ ПШ. Стоит отметить, что данный факт не отразился на площадях ПШ двух полушарий и магнитных потоках через них. Высокая межполушарная корреляция магнитных потоков через ПШ ( r =0.84, рис. 3, в ) подтверждает ожидаемую синхронность процессов пересоединения цикла Данжи в северной и южной долях магнитосферного хвоста.

ЗАКЛЮЧЕНИЕ

В данной работе продолжена начатая в [Лунюш-кин, Пенских, 2019] разработка нового наземного метода автоматической диагностики границ АО на основе выходных данных ТИМ и выполнено расширение этого метода на Южное полушарие. На примере анализа, проведенного для одной из суббурь, показано, что точность автоматического метода определения границ АО в двух полушариях не уступает ручному способу. Реализация геомагнитного метода автоматической диагностики границ АО в двух полушариях Земли вошла в качестве важного модуля в единый программный комплекс ТИМ. Геомагнитный метод проведения границ АО, как и весь модернизированный программный комплекс ТИМ, в настоящее время позволяет проводить мгновенные расчеты в обоих полушариях автоматически, без активного участия человека.

В работе показано следующее: полученные геомагнитным методом границы АО качественно соответствуют одновременным снимкам овала полярных сияний со спутника IMAGE, а также результатам моделей OVATION и APM; граница обращения ионосферной конвекции, определенная геомагнитным методом в двух полушариях, согласуется с картами электрического потенциала ионосферы по модели SuperDARN-RG96.

Практическая значимость геомагнитного метода диагностики границ ПШ подтверждена на примере избранной изолированной суббури фактом синхронного изменения ПШ в двух полушариях и магнитных потоков через них в ходе развития трех основных фаз суббури.

Разработанный нами геомагнитный метод автоматической диагностики границ авроральных овалов в ионосферах двух полушарий Земли по данным наземной мировой сети магнитометров является новым и перспективным инструментом в исследовании процессов взаимодействия в системе солнечный

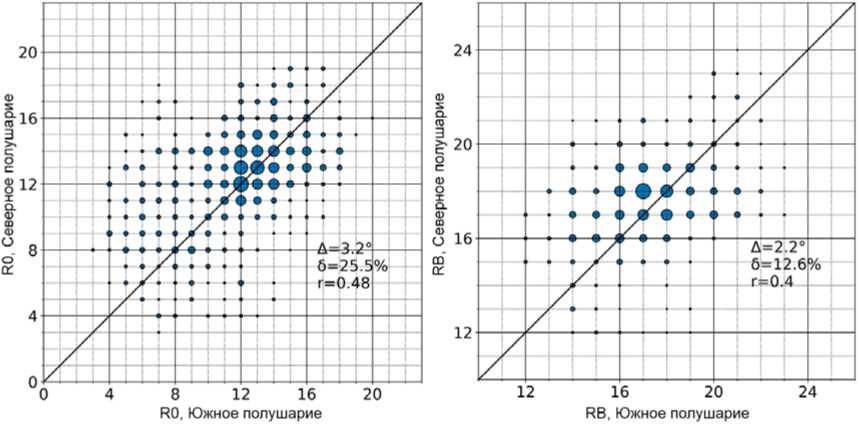
Рис. 9 . Статистическое межполушарное сравнение границ для R0 (слева) и RB (справа), построенных автоматическим методом для суббури 27.08.2001. По осям абсцисс и ординат — кошироты соответствующих границ

ветер — магнитосфера — ионосфера и в решении актуальной проблемы магнитосферных суббурь.

В отличие от радаров, спутников и GPS используемая нами база данных SuperMAG содержит более длительные временные ряды непрерывных измерений поля геомагнитных вариаций. Модернизированный метод ТИМ-ИСЗФ обладает достаточно хорошим пространственно-временным разрешением и дает мгновенную крупно-масштабную картину эквивалентных токов, электрических полей и продольных токов одновременно в двух полушариях Земли. Кроме того, метод ТИМ-ИСЗФ значительно дешевле других инструментов.

Авторы благодарят В.В. Мишина, А.В. Тащилина, В.Г. Воробьева, О.И. Ягодкину и А.Г. Яхнина за интересные дискуссии и полезные замечания при обсуждении основных результатов настоящей статьи на 43-м ежегодном семинаре «Физика авроральных явлений» (ПГИ КНЦ РАН, март 2020 г.).

Мы выражаем свою признательность создателям SuperMAG [], APM [], SuperDARN-RG96 [], OVATION [ typ_redirect], OMNI [ form/] за возможность использовать эти базы данных и модели в нашем исследовании.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-3590046.