Геометрическая квазидискретная модель группового преследования одиночной цели

В рассматриваемой задаче вводится период дискретизации времени, когда преследователь делает шаг и меняет направление движения. Используя квазидискретную модель в задаче преследования, можно аппроксимировать динамический процесс преследования с последующей визуализацией этого процесса.

В статье обсуждаются вопросы следования преследователем, в которых траектории цели и преследователя предварительно смоделированы. Предполагается, что траектория, отвечающая заданным требованиям, автоматически моделируется в каждый момент времени. Рассматривается группа из четырех преследователей.

1. Моделирование траектории преследователя

Преследователь начинает движение из точки Р со значением скорости V_P и настигает цель в точке Т, причем траектория преследователя должна быть сконструирована таким образом, чтобы попадать в точку Т по направлению вектора V P . Траектория движения состоит из прямолинейного отрезка, соединяющего точки Р и P_tan , и из дуги ТГ^т радиуса Rp (рис. 1, а).

На второй участок моделируемой траектории накладываются граничные условия: радиус кривизны не должен быть меньше R_p , а угол подхода к цели определяется вектором скорости V P . В тес-

товой программе этот вектор перпендикулярен вектору скорости цели V_T . Центр дуги ТТР От , отвечающей заданным условиям, определяется вы-

ражением:

С т = Т ₊ RpJ—^L\

V    Лт1/

Для определения точки P_tan сопряжения прямой (Р, P_tan ) с дугой Т, P_tan реализована процедура – функция, формирующая локальную систему

координат     с     ортами     е1     и

Ст-P    „     Г-е1 у"!

ез = ------, е₂ =  „   . Точка С_т в этой системе

1     |Ст-Р|'     2 L е1х J координат преобразуется к виду:

Г(Ст - Р) -еа_

. Отсюда находим координаты точ-L ⁽С т — Р) • cj

Г Г — [ 1(СТ — Р)11 ки сТ.п : сТ.п = [     QJ

Если модуль вектора |(C_T —Р)| равен С_х (рис. 1, б), то в локальной системе координат

(е 1 , е₂) координаты точки сопряжения P_tan . _п удовлетворяют системе уравнений в локальной системе координат (е 1 , е₂) с центром в точке Р:

^(Ptan .п   ^СТ.п ) • ^(P tan .п    ^СТ.п )     ^RP ,

^(P tan .п

—

^CT.n ) • ^Ptan .п °"

В системе координат (е 1 , е₂) с центром в точке Р эта система уравнений имеет решение:

Г          C x ² —R p          ’

1 tan .п

±

С х

RP^(C x +R p )x-Rp)

С х

.

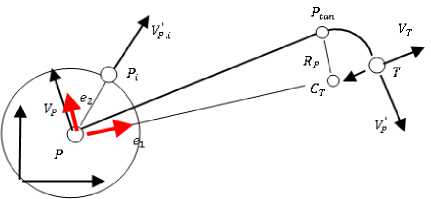
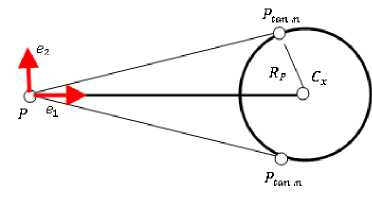
Рис. 1, б. Определение точки сопряжения в локальной системе координат

Рис. 1, а. Предполагаемая траектория следования преследователя

Для преобразования координат точки P_tan . _n в мировую систему координат (Н₂, Н 2 ), где Н₂ = [1] , Н 2 = [0], необходимо получить выражения для базиса (Н ₂, Н 2 ) относительно базиса (б₂, 6 2 ):

Н1 '62          Н • 61

^ = к • 62J,  " = [н2 •62J. В частности,коор-

v_p где ^V 2 = IT P ! точки P tan

р.

tan .v

[ ^(Ptan ^(Ptan

V 2 = [ ^vi"^y( (рис. 2, а). Координаты в этой системе координат равны

—

—

P) • ” 2

P) • ” 2

], а координаты точки P_iV

равны:

динаты точки P_tan . _n в мировой системе координат равны: P_tan = [Q^{tan .n} ^²1 + P. В программе реа- ^Ptan .n • ^ 2

лизован вариант, когда точка P_tan . _n находится в

P i.v

|ИР|^ДТ • cos(Шp•ДТ)l if Ptanvy - 0 [|yP| • ДТ • sin(^P • ДТ)]

|УР|^ДТ^ cos(Шp•ДТ) . if Ptanvy < 0 [—|yP| • дт • sm(Wp • ДТ)]

верхнем положении.

В рамках квазидискретной модели задачи преследования введем в рассмотрение период дискретизации ДТ. При этом шаг преследователя имеет величину |Vp| • ДТ. Если минимальный радиус кривизны равен Rp, то угловая частота вращения точки P равна toP = —. Угол подхода к цели дис-rp кретно изменяется с шагом toP • ДТ.

Если угол к меньше, чем угол to_P • ДТ, то координаты точки P_iV определяются выражением

if Ptan .Vy

|VP| 'ДТ' cos(«)l - 0 L|Vp| 'ДТ' sin(«)]

|Vp|•ДТ• cos(«)  .

< 0 L—|Vp| 'ДТ' sin(«)]

Угол к - это угол

между вектором P tan.v

вектором ”₂ . Переводя координаты точки P_iV

и из

2. Определение координат точки касания в системе координат преследователя

В рассматриваемой квазидискретной модели преследователь должен догнать цель таким образом, чтобы в момент совпадения координат (преследователя и преследуемого объекта) преследователь имел заданный вектор скорости и круговую траекторию с радиусом кривизны, не превышающим допустимой величины. Рассмотрим систему координат (v₂,v₂ ) с началом в точке P .

системы координат (v₂,v₂ ) в мировую систему координат, получаем выражения для базиса (Н 1 ,Н 2 ) в базисе (v₂, v₂ ):

^ e = 1Н1 '”2 ]

²      Н • ”21

h2V    [h2 ■ i>2]'

где Н 2 = Щ. Н 2 = Q.

На следующем этапе итераций положение преследователя   P_i  определяется выражением:

P-=[

'Pi.v • ^2.

-Piv • ^2.

.V

. .V

I + P, то есть траектория преследо-

вателя P_i приближается к прямой линии (P, P_tan ).

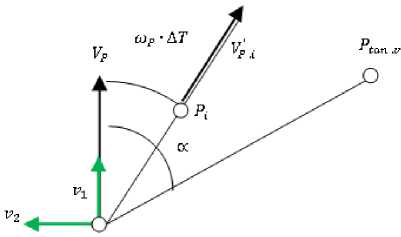
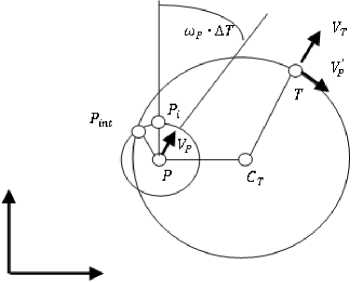
Рис. 2, б. Анализ координат точек пересечения окружностей

Рис. 2, а. Выбор направления движения преследователя

3. Координаты точек пересечения круговых траекторий

Рассмотрим случай, когда между преследователем Р и центром окружности С_т расстояние меньше минимального радиуса кривизны траектории R_P преследователя. На рис. 2, б представлены две пересекающиеся окружности с радиусами r_P и R_P . Точки Р и С_т - центры точек, где r_P = ш_Р • ДТ. Требуется определить координаты точки P_i как функции координат точек P_int пересечения двух окружностей в системе координат (б₁, 6 2 ) с центром в точке Р, где

|Ур1^ДТ • cos(Шp•ДT)l

lJ Рш,ру - 0 [|УР| • дт • sin(Wp • ДТ)] i,p =                 |vp| •дт^ cos(Шp•ДT) .

lJ Рш,ру < 0 [—|Kp| • дт • sin(^Р • ДТ)]

Если угол к меньше, чем угол to_P • ДТ, то координаты точки P_{i р} равны:

^•дт^ cos(K)l

lJ PjntрУ- °[|КР|-ДТ- sin(K)|

1" "ifP <0 [ ^^ cos(K) .

IJ Pjnt, py

Угол к - угол между вектором P_int , _р и векто

Ст —Р е1 “ |Ст—Р| ’

«2- [—3

ром р1.

Преобразуя координаты P_i , _р из системы координат (р₁,р₂) в мировую систему координат, получаем выражения для базиса (Н₁,Н₂) в базисе ⁽Р 1 ,Р 2 ):

В системе координат (б1, 62)  выражения для координат точки Pint ,n имеют вид:

р. .   = int ,n	С Х —R p +r p2                       ■ 2^С х
, ^(С Х +R P	-r p )• ( С x —R p +r p )• ( R p —С x +r p )^ ( R p +С х +r p )
±
	2^С х

^ [

' Н1 • р1 . Н • Р2

]   ^,р    [Н • ^2],

где H i = [0], Н 2 = [1].

Отсюда находим выражения для координат преследователя Pi на следующем этапе итераций:

В предлагаемом алгоритме основное внимание уделено верхней точке (см. рис. 2, б). Переведем координаты P_int , _n в мировую систему координат: P_int = [p^{int ,n} ,1 ] + Р, где векторы h₁ и И.2

^P int .п • ^Л 2

P i

■ Рр • ^.pl

-^Pi,р • ^ 2,pJ

+ Р.

Таким образом, рассмотрен алгоритм перехода преследователя на дугу РЗ-Т (см. рис. 2, б).

определяются выражениями

'■' = ^[Н 1 •Й ’  ^А 2

где Н , = [Ц, Н 2 = [1].

Н • 611

.Н 2 • е 2 ^]

Для определения координат точек пересече-

ния окружностей перейдем в систему координат (р₁,р₂ )     с     началом     в     точке      Р:

^Р 1 = Si ^Р 2 = ^[v2^У](рис.3,^а).

В системе координат (р₁, р₂) координаты точки P_int определяются выражением:

(Pint — Р) • Pi] [(Pint— Р)^2 Г

Координаты Р_1р в системе координат (р₁,р₂) с началом в точке Р имеют вид:

4. Случай непересекающихся окружностей

Рассмотрим случай |Р — С_Р| < R_P — г_р .В этой ситуации следует поставить точку P_int на оси (Р,С_Р) слева от точки Р (см. рис. 3, б). В системе координат (е₁, е₂) с центром в точке С_т эта точка имеет координаты P_int , _n = [ ^^Р]. Требуется рассчитать угол « между вектором У_Р и вектором РЖ.

Если угол « меньше, чем угол ш_Р • ДТ, то координаты точки P j , _р на следующем шаге итераций в системе координат (р₁,р₂) с началом в точке Р

определяются выражением

|VP| • ДТ • cos(K)l i,p [|^р|^ДТ- sin(«)].

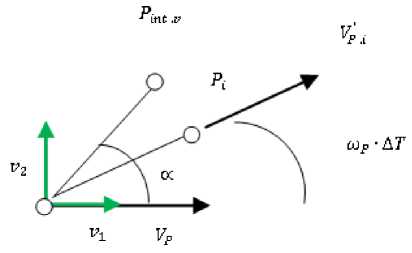
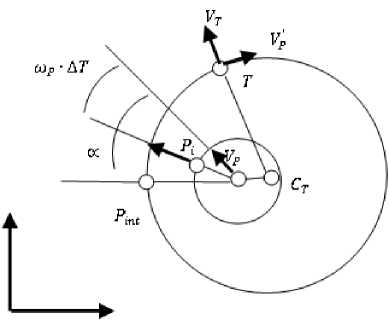
Рис. 3, б. Случай непересекающихся окружностей

Рис. 3, а. Анализ в системе координат преследователя

Если при этом точка Т в системе координат (е 1 , е₂) с центром в точке С_Т находится в верхней полуплоскости, то

|^Р| 'ДТ' cos(k)1

Lr   L|Vpj•ДТ• sin(K)], а если в нижней полуплоскости, то

ния ш 1 , ограничим радиус кривизны траектории j^ i j движения преследователя величиной R1 = —.

Для реализации стратегии преследователя Р 1

Р .г

—

Г|УР1 'ДТ' cos(k) [|р| 'ДТ' sln(K)|.

надо выполнить теме координат точке Р 1 , где

расчет координат точки Т в сис-(" 1 , г₂) с началом координат в

Если же угол к больше, чем угол ш_Р • ДТ, то координаты точки Р " _г определяются выражением

|Vpj• ДТ • cos(шp•ДТ)

"."   L|VP|•ДТ• sin(wP•ДТ)].

При этом также реализуются две возможности: если точка Т находится в верхней полуплоскости, то

|Vp| • ДТ' cos(wp 'ДТ)!

"."   L|VP|•ДТ• sin(wP•ДТ)], а если в нижней полуплоскости, то

Vp ^Г1= ^ " 2 =гг]. Получаем координаты точки T v :

т = [ '"

(Т — Р) • "i (Т — Р) • "2].

Рл, =

—

Г| V | • ДТ • cos(toP • ДТ)1 Ljvpi • ДТ • sin(wP •ДТ)].

Рассмотренная ситуация встречается, когда скорость преследователя намного превышает скорость цели или очень мала угловая скорость преследователя.

5. Цель и стратегия первого преследователя

Пусть преследователь P 1, движущийся со скоростью V 1, догоняет объект T . «Догнать объект» – означает совместить координаты точек Р 1 и Т с точностью |Р 1 — Т| <  е, где е = |V 1 | • ДТ (ДТ - период дискретизации). Полагая, что объект Р 1 имеет максимальную угловую скорость враще-

Исследуя положение точки Т_г, определяем ее принадлежность верхней или нижней полуплоскости в системе координат (г 1 ,г₂) с началом координат в точке Р 1 (рис. 4, а):

|V1|•ДТ• cos(^i • ДТ)1

= "7'", - 0 [|р|'ДТ' sin(^i 'ДТ)]

1"                |И11'ДТ' cos(^i 'ДТ) .

I/ '", < 0 [_j711 • ДТ • sin(^1 • ДТ)]

В процессе расчета сравниваем значения углов ш 1 • ДТ и к, где к - угол между векторами Р_гТ и V i - Если угол к меньше угла ш_Р • ДТ, то координаты точки Р_1г равны:

Р г

ifT >ol^р^'c°s:

У '", - 0 [|уР|.ДТ-sln(«)]

IfT <0[ ^|Г Р |'^ДТ' ^С0=^(е) .

У Л’ <0 1-|ГР| • ДТ • sln(«)]

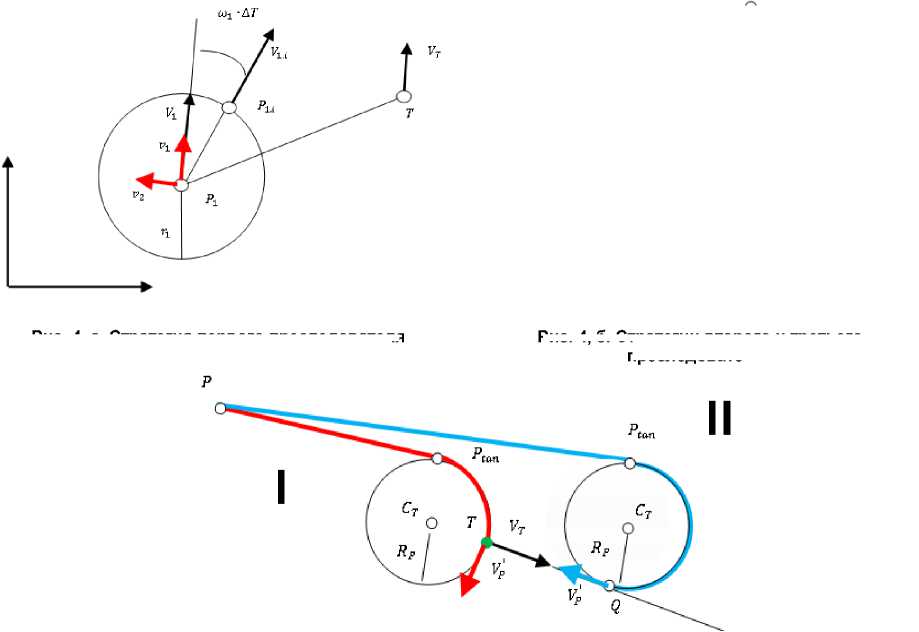
Рис. 4, в. Стратегия преследователя из «засады»

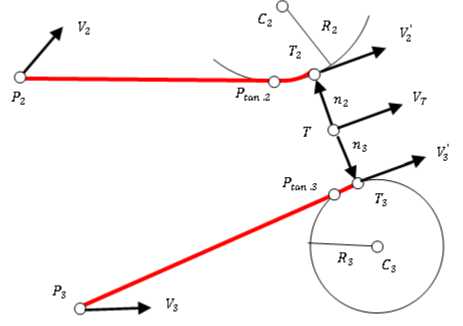
Рис. 4, а. Стратегия первого преследователя

Рис. 4, б. Стратегии второго и третьего преследователей

• 6.    Цели и стратегии

второго и третьего преследователей

Преследователи Р₂ и Р₃ движутся со скоростями V 2 и V₃. Их целью является совмещение (с определенной степенью точности г) точек Т₂ и Т₃ (рис. 4, б). Координаты точек Т₂ и Т₃ формируются в виде:

^Т 2,3 = ^Т + ^ 2,3 .

Введем в рассмотрение векторы нормалей

п2 3 = ±-1-   Vryl • Д52 з,

2,3        IV7-1   VT           2, где Д52,3 - расстояния от точек Т2 и Т3 до точки Т.

Объекты P₂ и P₃ должны подходить к точкам Т₂ , Т₃ со скоростями V₂', V₃ ’ . Радиусы кривизны траекторий этих объектов не должны быть меньше Д_{2 3} = '" ^2,3 ' , где ш_{2 3} - максимальные угловые ско-^,         ш 1,2                '

рости вращения преследователей Р2 и Р3.

Напомним, что в каждый момент времени моделируемая траектория состоит из прямолинейного участка VP 23 ,P tan23 \  и сегмента дуги

P_t an: ₂ , ₃,Т₂ , ₃ . На каждом шаге итераций объекты Р₂ и Р₃ выполняют поворот на угол Дю и поступательно перемещаются на определенное расстояние. В предлагаемом алгоритме объекты Р₂ и Р₃ начинают движение со скоростью V_Т , как только выходят на курс, параллельный курсу преследуемого объекта Т.

• 7.    Цель и стратегия

• 8.    Цель и стратегия объекта преследования

четвертого преследователя

Если условно классифицировать первого участника как главного «загонщика», а второго и третьего участников полагать его помощниками, то четвертого участника можно назвать игроком из «засады».

На рис. 4, в представлены два случая. В первом случае траектория преследователя заканчивается непосредственно в точке цели Т, причем в этой точке вектор скорости преследователя перпендикулярен вектору скорости цели V. Во втором случае вектор скорости точки Q направлен противоположно вектору скорости цели Vr. Точка Q расположена на прямой линии, проведенной из точки Т по направлению вектора Vr (см. рис. 4, в). Если произвольно ука- зать точку Q в любой точке плоскости преследования, то мы не сможем достичь цели.

После достижения точки Q можно изменить стратегию преследователя. Например, скорость может быть снижена до нуля. В этом случае стратегия сводится к ожиданию момента приближения цели на расстояние, меньшее г.

После достижения точки Q стратегия четвертого преследователя может совпадать со стратегией первого преследователя.

Цель объекта преследования в рассматриваемой модели – уклонение от первого преследователя.

На рис. 5, а показана стратегия преследуемого объекта. Объект Т, движущийся с поступательной скоростью V_r и с угловой скоростью ш_Т , совершает за период дискретизации ДТ поворот на угол ш_Т • ДТ и перемещается на расстояние \Т₄ — Т| = iV_r| • ДТ. Направление вращения точки Т зависит от того, в какой полуплоскости находится преследователь Р 1 .

В качестве альтернативной стратегии может быть избрана стратегия «параллельной скорости», показанная на рис. 5, б, из которого видно, что объект преследования Т изменяет направление вектора своей скорости V, стремясь двигаться параллельно направлению вектора скорости преследователя V 1 . Стратегия параллельной скорости предпочтительна, если преследователь находится далеко от цели. Когда преследователь приближается на дистанцию нескольких итерационных шагов (дистанция «последнего прыжка»), для цели становится выгодна стратегия уклонения (см. рис. 5, б).

Выводы и заключение

На основе материалов, представленных в статье, составлен программный модуль в пакете компьютерной графики MathCAD, рассчитывающий траектории движения группы из четырех преследователей и цели, уклоняющейся от преследователей.

Каждый участник погони в рассматриваемой геометрической модели имеет свою собственную цель и стратегию. На рис. 6 показан кадр видео-

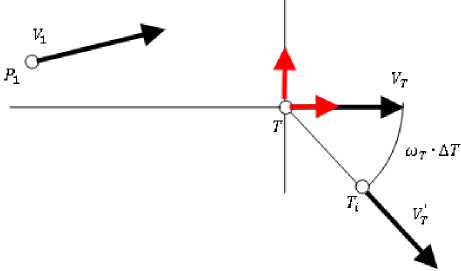
Рис. 5, а. Стратегия объекта преследования

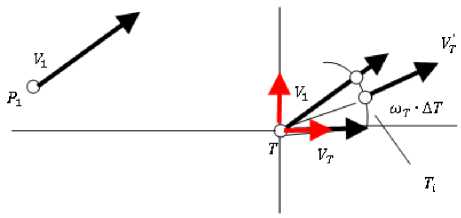
Рис. 5, б. Дополнительная стратегия объекта преследования

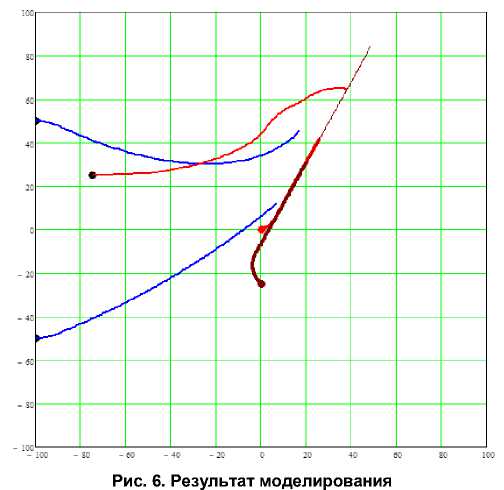
группового преследования одиночной цели

фильма, где один преследователь совершает погоню «по следу», а два преследователя догоняют цель по параллельной траектории. Еще один преследователь движется ортогонально к траектории цели. В разработанном программном модуле изменены цель и стратегия четвертого преследователя для упрощенного указания координат точек входа и векторов скорости в этих точках.

Статья подготовлена на основе теоретических положений, изложенных в работах [1–6]. Описание алгоритмов следования рекомендованным траекториям размещено на ресурсе [7]. На ресурсе [8] представлен видеофильм с результатами геометрического моделирования в рамках разработанного программного модуля. Исходный код программы доступен на ресурсе [9]. При создании и разработке алгоритмов использованы работы [10–20].