Геометрически обоснованный метод формирования атомных кластеров Морса больших размеров

В последнее время значительно вырос интерес к методам получения сверхмелкодисперсных кластерных структурных материалов (наночастиц).

Изучение механизмов структурирования самих наночастиц связано с тем, что образование функциональных структур из нанокристаллических кластеров позволяет придавать материалам новые электрические, магнитные и оптические свойства [1]. В частности, результаты последних исследований показали, что многие атомные кластеры обладают яркой люминесценцией в видимой области спектра [2]. Это делает молекулярные кластеры перспективными с точки зрения практического применения в устройствах фотоники: люминесцентных сенсорах, солнечных батареях, светодиодах белого свечения и т.д. Знание деталей формирования кластерной структуры является определяющим для повышения эффективности различных способов производства нанокластеров.

Основной задачей данного направления является обнаружение такой геометрической структуры атомного кластера, иными словами, конформации кластера, которая соответствует минимуму энергии взаимодействия входящих в него атомов. В более простом случае конформационного анализа химическая связь между атомами не учитывается. В частности, для кластеров Морса рассматриваются только парные взаимодействия атомов кластера, которые описываются потенциальной функцией:

v ( r_ij ) = e ^{ρ (1 - rij )} ( e ^{ρ (1 - rij )} - 2), (1)

где r ij – расстояние между атомами i и j; ρ – параметр, расширяющий или сужающий потенциальную «яму» парных взаимодействий атомов в кластере Морса [5]. Обычно ρ принадлежит диапазону от 3 до 14.

Энергию взаимодействия всех атомов кластера можно вычислить как сумму энергий парных взаимодействий

NN

v ( X ) = 1 ∑ ∑ v ( r ij ),                             (2)

• 2 i = 1 j = 1

( i ≠ j )

где X = ( x 1 ,…, x N )′, x i ∈ R ³ – координаты центров атомов кластера.

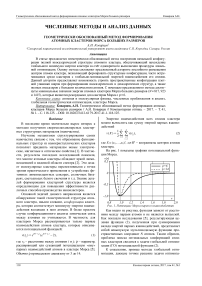
На рис. 1 показаны графики потенциальной функции Морса.

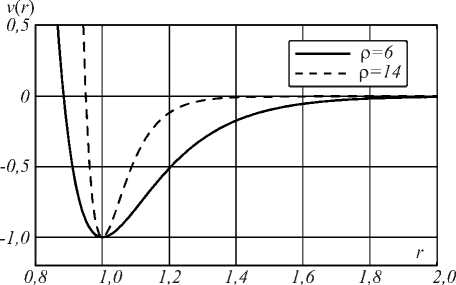
Рис. 1. Потенциал Морса парного взаимодействия

Как видно из рисунка, функция зависит от расстояния между парами атомов и не является выпуклой. Как показали исследования [5], результирующая целевая функция (2), полученная при суммировании вклада энергий парных взаимодействий, представляет собой невыпуклую мультимодальную функцию пространственных координат N атомов. Таким образом, проблема поиска оптимальных конформаций атомных кластеров сводится к задаче глобальной оптимизации (ГО) потенциальной функции (2).

К сожалению, прямые методы глобальной оптимизации, дающие точное решение задачи оптимиза- ции, способны находить решение (даже с использованием современных суперкомпьютеров) для функций с числом 20 – 30 переменных [3], в то время как в задачах ГО атомных кластеров участвует более 900 оптимизируемых переменных.

В сложившейся ситуации приходится разрабатывать эвристические алгоритмы оптимизации, использующие разнообразную дополнительную информацию об объекте исследования [4].

Одна из первых эвристик, применяемых при решении задачи ГО кластерных структур, заключается в использовании геометрических свойств известных атомных кластеров [5, 23]. Например, для кластеров Морса было замечено, что расположение атомов в оптимальных конформациях тяготеет к симметричной сферической форме [6]. Использование этой информации привело к созданию геометрически обоснованных методов глобальной оптимизации кластеров Морса. К идее учёта геометрических структурных свойств кластера для минимизации его потенциальной энергии впоследствии не раз возвращались [7– 10]. Так, в работе [7] в качестве ядер начальных конформаций кластеров использовались икосаэдрические, додекаэдрические или гранецентрированные кубические структуры.

Ещё большую группу методов оптимизации кластеров образуют локально-стохастические методы, использующие идею метода «basin-hopping» [5]. Основу этих методов составляет представление о том, что для потенциальной функции (2) локальные экстремумы собираются в ограниченном количестве так называемых «бассейнов», в каждом из которых «воронки» локальных минимумов расположены настолько близко друг к другу, что за счет случайных возмущений координат атомов кластера возможен постепенный переход от локальных экстремумов к глобальному. Эта идея многократно совершенствовалась [11 – 14], что в конечном итоге позволило найти глобальные эвристики для кластеров больших размеров [13].

И, наконец, следует упомянуть группу популяционных алгоритмов глобальной оптимизации [15 – 17], которые в отдельных случаях значительно повысили эффективность эвристических алгоритмов ГО атомных кластеров Морса.

В данной статье рассматривается геометрически обоснованный метод глобальной оптимизации атомных кластеров Морса больших размеров.

1.    Плотная упаковка атомов кластера

Задача формирования атомных кластеров минимальной потенциальной энергии так или иначе связана с проблемой плотной упаковки шаров [6, 24]. Для кластеров наиболее важными факторами являются: сферичность формы конформации и достижимость как можно более плотной «упаковки» атомов.

Для жестких шаров наибольшая плотность достигается для гранецентрированной кубической решётки. В этом случае шары заполняют чуть больше 74 % объёма пространства [18]. Однако для «мягких» атомов кластера Морса, когда атомы могут частично

«вминаться» друг в друга (см. левую ветку графика потенциала парного взаимодействия на рис. 1), более плотные упаковки формируются для икосаэдриче-ских и додекаэдрических сеток [5, 7, 21, 23].

Анализ кластерных структур из базы данных Кембриджского университета [19] и её расширения [20] для ρ ≥ 6 с числом атомов 12 <  N <250 показал, что представленные атомные структуры с глобальнооптимальным потенциалом энергии при ρ =6 в подавляющем большинстве случаев имеют икосаэдри-ческую или ей подобную структуру. Более того, для магических чисел N = 55, 147, 309, 561 конформации имеют форму полного правильного икосаэдра. В то же время при ρ = 14 преобладают додекаэдрические и икосаэдрические структуры, хотя нередко встречаются гранецентрированные решетки и плотноупакован-ные конфигурации (close-packed) [19, 20].

Одним из важных результатов, выявленных в ходе анализа атомных кластеров Морса с глобальнооптимальным потенциалом энергии, является тот факт, что кластеры можно развернуть вдоль оси z таким образом, что их атомы будут образовывать «нечеткую» слоистую структуру. Под «нечетким» слоем в данном случае понимается расположение группы атомов (шаров) таким образом, чтобы их центры находились не на плоскости, а в достаточно «тонком» слое z j ± ∆ z j .

Второе важное наблюдение заключается в том, что в проекции на плоскость x0y все выделенные слои в оптимальных кластерах образуют икосаэдрическую нерешётчатую упаковку. Назовём её икосаэдрической

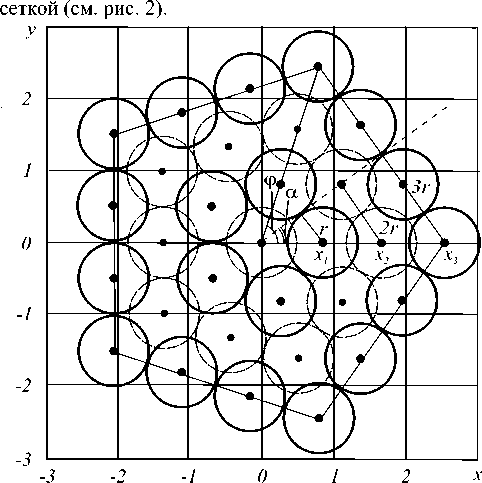
Рис. 2. Проекция на плоскость икосаэдрической нерешётчатой упаковки шаров

Эти два факта позволяют предложить более простой метод формирования полных правильных икосаэдров для кластеров любого размера, которые могут служить хорошими начальными приближениями для алгоритма локальной оптимизации, уточняющего конечные конформации кластеров.

В свою очередь, рекордные конформации, построенные для магических чисел, являются полезными ориентирами для формирования кластеров промежуточных размеров. Они могут быть построены либо «наращиванием» предшествующего полного икосаэдра, либо «разборкой» последующего. Построить икосаэдрическую сетку достаточно просто.

В центре упаковки располагается шар радиуса r (в нашем случае r = 0,5). Плоскость делится лучами, исходящими из начала координат, на 5 равных частей. Угол между лучами равен φ =2π /5. Пусть α = φ /2= π /5. Далее будем располагать центры шаров по линиям правильных пятиугольников вокруг центрального шара. Причем для первого пятиугольника в каждом секторе размещается две половинки шаров (фактически один целый шар), для второго пятиугольника в каждом секторе – 4 половинки (2 целых шара) и т.д. В этом случае координаты шаров, расположенных на оси 0x (y =0), для каждого из пятиугольника несложно вычислить по формуле xm = mr/sinα = mr/sin(π/5), (3)

где m – номер пятиугольника.

Координаты остальных шаров можно найти из геометрических соображений. Если центральный шар условно считать нулевым «пятиугольником», а каждый слой формировать объединением из пятиугольных конфигураций только с четными или нечетными номерами. Располагая слои в пространстве друг над другом, можно получить икосаэдрическую нерешётчатую упаковку шаров. В отличие от гранецентрированной кубической упаковки шаров (ГЦКУ), где каждый из слоёв размещается фактически над предыдущим слоем, слегка «утопая» в «углублениях» предыдущего слоя, в нашем случае чётные и нечётные слои почти наполовину «входят» друг в друга так, что нечётные слои находятся внутри чётных (см. рис. 3).

Рис. 3. Икосаэдрическая нерешётчатая упаковка шаров (4 чётных слоя и 3 нечётных)

2.    Формирование пятиугольных конфигураций шаров

Практически все известные методы ГО атомных кластеров используют технику локальной оптимизации кластера из положения, близкого к оптимальному решению, поскольку сложность алгоритмов локальной оптимизации имеет полиномиальный характер. Из практики уже давно было замечено [2, 21, 23], что ико-саэдрические структуры или близкие к ним являются хорошим начальным приближением для поиска гло- бального минимума потенциальной энергии кластера методами локальной оптимизации. В данном параграфе опишем метод построения таких структур, основанный на послойном формировании всего кластера.

Определение координат центров шаров в секторе базового пятиугольника

Каждый слой конформации строится следующим образом.

Пусть α = 2 π /5; β = 2 π /10 (рис. 4), и на каждой стороне размещается m шаров. Из (3) следует, что координату x m 1 можно вычислить по формуле x m 1 = mr /sin ( π /5), а координаты центра первого шара равны X m 1 = ( x m 1 , 0). Несложно вычислить параметры a и b (рис. 4):

f a = 2 r sin в ,

[b = 2r cos в, и угол луча, проходящего через центр второго шара, γ2= arctg (a /(xm1–b)). По аналогии, угол луча k-го шара вычисляется по формуле:

γ _k = arctg

a ( k - 1) x_{m 1} - ( k - 1) b

, k = 1,... m .

Координаты центров шаров сектора расположены на пересечении лучей под углами γ k и прямой, проходящей через центры 1- го и m -го шара сектора. Несложно вычислить координаты центров шаров, лежащих на стороне пятиугольника X mk = ( x mk , y mk ), где

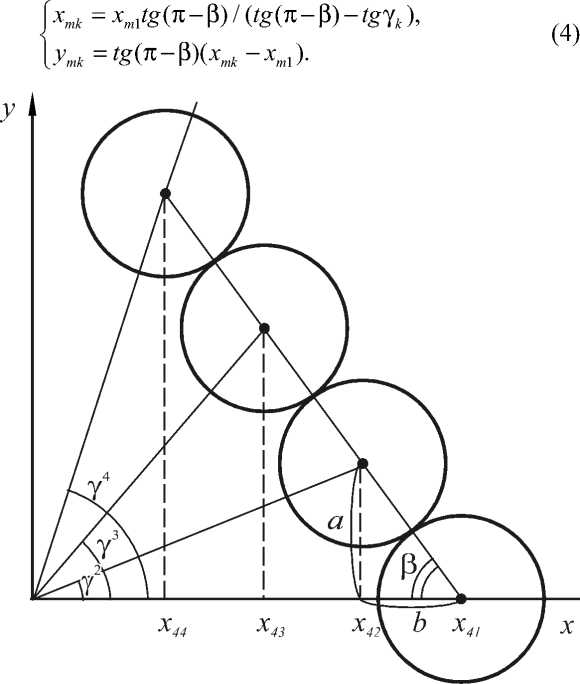
Рис. 4. Вычисление координат центров шаров в секторе базового пятиугольника

Координаты центров шаров остальных четырёх секторов определяются за счет четырёхкратного вращения первого сектора на угол α. В базовом варианте пятиугольника на каждой его стороне располагается m шаров, а в вершинах пятиугольника располагается один шар. Такую конфигурацию обозначим I(m,1). Структура, представленная на рис. 3, составлена из базовых конфигураций.

Определение координат центров шаров в секторе деформированного пятиугольника

Из базовых конфигураций пятиугольников невозможно построить икосаэдр. Необходимо деформировать структуру пятиугольника за счёт «переноса» части шаров с границы сектора в его вершину. Фактически это приводит к формированию неправильных десятиугольников.

В случае размещения в вершинах пятиугольника k шаров произведём следующие преобразования.

Для вершины, расположенной на луче 0x, когда k – нечётно, относительно k-й вершины, вершины с номерами k-1,…,1 расположим под центром k-го шара, т.е. перпендикулярно лучу (см. рис. 5) так, чтобы они касались друг друга только в одной точке. То же самое проделаем с шарами на втором луче пяти- угольника, проходящем под углом а по отношению к

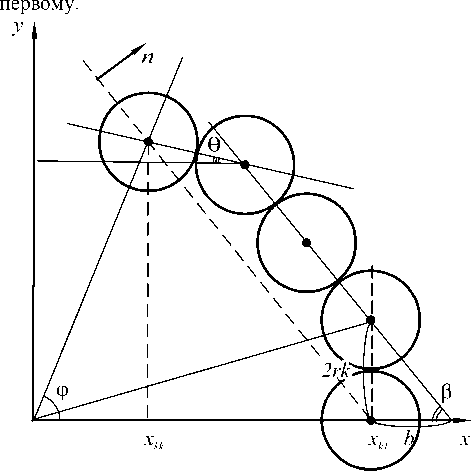
Рис. 5. Вычисление координат центров шаров в секторе деформированного пятиугольника

По построению 6 = п /2- ф = п /10. Пусть в секторе содержится m шаров. Очевидно, что центр первого шара сектора после перемещения опустится ниже оси абсцисс. Следовательно, всю эту конфигурацию необходимо «поднимать» за счёт её перемещения в направлении вектора n (перпендикулярного к границе сектора шаров) на величину z .

X mj = X mj + Zn . (5)

Здесь n = (cos( n /5); sin( n /5)), j = k ,..., m - k .

Тогда, для j = 1,…, k центры шаров вычисляются по формулам:

x mj = x m , k + 1 ^,

У m = У m , k + 1 — 2 r ( k — j + 1).

Координаты центров вершинных шаров второго луча для j = m – k ,…, m определяются по формулам:

x mj = x m , m - k ^{- 2} r ^{( j -} m ^{+ k} ) cos ^{6 ,} y mj = y m , m - k ^{+ 2} r ^{( j -} m ^{+ k} ) sin ⁶-

В качестве естественного условия завершения процесса перемещения конфигурации шаров сектора выступает уравнение:

X m ,1 = 0.

Решив уравнение (8) относительно z по формулам (5)–(7), можно определить координаты центров шаров первого сектора деформированного пятиугольника. Остальные координаты вычисляются по аналогии с базовым случаем.

Данная методика позволяет формировать деформированные «пятиугольники» с нечётным количеством шаров в его вершинах. Если вместо уравнения (8) использовать уравнение

/V xm ,1 = r,

то получится деформированный «пятиугольник» с чётным количеством шаров в его вершинах.

Деформированные пятиугольники с заданным количеством шаров в его вершинах будем обозначать I(m, k), где m – число шаров в секторе, k – в вершине. На рис. 6 представлены три возможных варианта «пятиугольников» для m = 3: I(3,1) – базовая конфигурация (рис. 6a); I(3,2) и I(3,3) – деформированные пяти- угольники с двумя и тремя шарами в вершинах (рис. 6б, в).

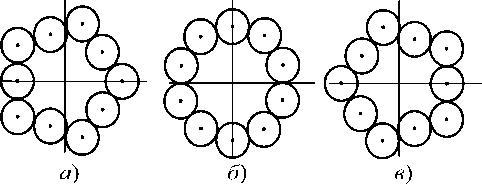
Рис. 6. Конфигурации пятиугольников: базового и деформированных

Из рис. 6 видно, что в последней конфигурации вершины пятиугольника поменялись местами с его сторонами. Этого можно добиться, повернув базовый пятиугольник на угол а.

3.    Построение икосаэдрических плотных упаковок атомов кластера

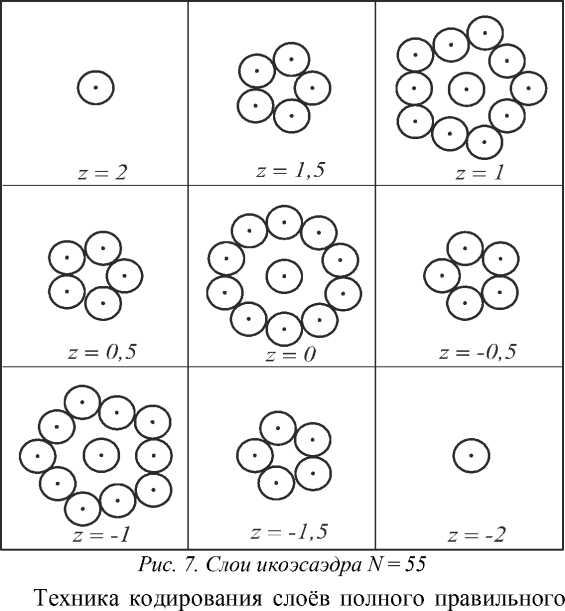
Предложенный способ построения различных конфигураций пятиугольников шаров даёт широкие возможности для формирования начальных приближений икосаэдрических плотных упаковок атомных кластеров. Например, схему структуры кластера из N =55 атомов можно описать следующим образом:

5 = [[ I (1,1): z = 2]; [ I (2,1): z = 1,5]; [ I (1,1), I (3,1): z = 1];

[ I (2,1): z = 0,5]; [ I (1,1), I (3,2): z = 0]; [ I (2,2): z = - 0,5];

[ I (1,1), I (3,3): z = - 1]; [ I (2,2): z = 1.5]; [ I (1,1): z = 2].

Меткой z здесь обозначена третья координата слоя в упаковке кластера. Слои представлены списками пятиугольников. На рис. 7 показаны слои икоэсаэдра кластера N =55, а на рис. 8 – его трёхмерная модель.

икосаэдра достаточно проста. Например, для N = 147

конфигурация начального приближения строится следующим образом.

«Шапка» икосаэрда состоит из базовых конфигураций слоёв от одного шара до слоя, содержащего четыре шара на стороне пятиугольника:

5 1 = [[ I (1,1): z = 3]; [ I (2,1): z = 2,5]; [ I (1,1), I (3,1): z = 2];

[ I (2,1), I (4,1): z = 1,5]; [ I (1,1), I (3,1): z = 1]].

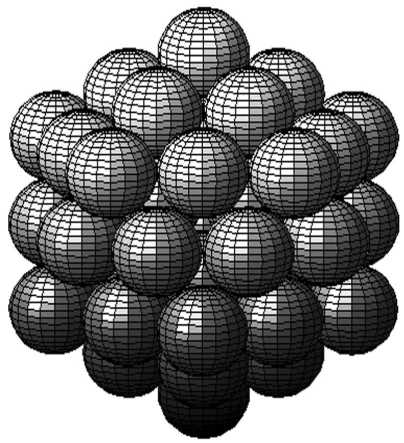
Рис. 8.Трёхмерная модель икоэсаэдра N = 55

Боковые грани икосаэдра содержат 10 треугольников с соответственно убывающим или возрастающим количеством шаров на грани от четырёх до одного и наоборот. Поэтому в слоях будем использовать деформированные «пятиугольники» с увеличивающимся на единицу числом шаров в вершинах пятиугольника.

5 2 = [[ I (2,1), I (4,2): z = 0.5]; [ I (1,1), I (3,2): z = 0];

[ I (2,2), I (4,3): z = - 0.5];[ I (1,1), I (3,3): z = - 1];

[ I (2,2), I (4,4): z = - 1.5]].

И, наконец, из фактически повёрнутых на угол а базовых пятиугольников достроим нижнюю часть икосаэдра.

5 3 = [ I (1,1), I (3,3): z = - 2]; [ I (2,2): z = - 2,5];

[ I (1,1): z = - 3]].

Весь икосаэдр описывается объединением слоёв:

= 5 1 U 5 ₂ U 5 ₃.

S 147

Следует отметить, что полные икосаэдры формируются только для p = 6. Для p = 14 преобладают до-декаэдрические структуры, начальные приближения которых формируются из базовых пятиугольников. Было замечено, что промежуточные конформации, расположенные между магическими числами при p = 6, формируются за счёт «деформации» икосаэдра путём переноса части его атомов на места центров шаров внешних пятиугольников. Поскольку координаты центров шаров икосаэдрической сетки известны, это обстоятельство позволяет разрабатывать эвристический алгоритм формирования конформаций начальных приближений для кластеров с размерами между магическими числами.

С помощью предложенного метода при p = 6 удалось рассчитать начальные приближения полных икоса-эдрических структур атомных кластеров Морса больших размеров для N = 147, 309, 561, 923 и 1415. Полученные приближения были уточнены с помощью решателя fminunc пакета Optimization системы MATLAB [22]. Удивительно, что для кластера N =923 (размерность задачи оптимизации 2769 переменных) решатель fminunc нашёл глобальный минимум потенциальной энергии кластера на обычном персональном компьютере за 18 часов. На рис. 9 представлена трёхмерная модель оптимального кластера Морса N = 923.

Рис. 9.Трёхмерная модель оптимального кластера Морса при N = 923

Точного доказательства глобальной оптимальности найденных решений нет в силу чрезвычайной сложности задачи глобальной оптимизации [3]. Однако результаты исследований с использованием многочисленных эвристических алгоритмов ГО кластеров Морса, накопленные за прошедшие 20 лет и собранные в базах данных [19, 20], позволяют с уверенностью предполагать, что найдены оптимальные решения, во всяком случае в диапазоне размеров N = 12–250. Для всех магических чисел, содержащихся в базе данных, кластеры при ρ =6 имеют форму полного правильного икосаэдра. Этот факт и совпадение потенциальных энергий для кластеров N =55, 147 и N = 309, 561 из работы [13] позволяют сделать предположение о глобальной оптимальности найденных конформаций.

В таблице приведены оптимальные конформации атомных кластеров Морса больших размеров.

Табл. Глобальные минимумы энергии атомных кластеров Морса больших размеров (ρ = 6)

N	υ( X )
55	-250,2866
116	-579,030
147	-760,631
178	-931,4886
258	-1399,628
309	-1710,202
485	-2761,9
561	-3235,560
817	-4802,61365
923	-5473,5
1415	-8560,523

Здесь полную икосаэдрическую структуру имеют кластеры N =55, 147, 309, 561, 923 и 1415. На два слоя меньше по отношению к кластерам N = 147, 309, 561 и 923 содержат кластеры N = 116, 258, 485, 817. Эти кластеры имеют не до конца оформившуюся икосаэдрическую структуру (псевдоикосаэдриче-скую). Псевдоикосаэдрическую структуру имеет и кластер N = 178, но в этом случае к полному икоэса-эдру, наоборот, добавляются два избыточных слоя. Глобальная оптимальность структур N = 116, 147, 178 подтверждается данными работы [19]. Из чего можно сделать предположение, что кластеры N = 258, 485, 817 также являются глобально-оптимальными.

Заключение

В данной работе представлены результаты оптимизации атомных кластеров Морса больших размеров, созданных на базе геометрически обоснованного метода. Основу метода составляет алгоритм формирования конфигураций пятиугольников для размещения центров атомов, с помощью которых строятся пространственные слои плотной упаковки шаров.

Предложенный способ позволяет достаточно просто формировать начальные приближения икосаэдри-ческих структур, оптимизация которых реализует глобально-оптимальные конформации атомных кластеров Морса для ρ =6.

В дальнейшем предполагается использовать ико-саэдрические сетки для формирования начальных приближений атомных кластеров с неэкосаэдриче-скими структурами.

Работа выполнена при государственной поддержке Министерства образования и науки РФ, а также гранта РФФИ №16-41-630637.