Геометрические аспекты контактного взаимодействия балансов в корообдирочном барабане

Подготовка древесины к использованию в целлюлозно-бумажном производстве требует ее очистки от коры. Эта технологическая операция выполняется в настоящее время с применением корообдирочных барабанов. В целях совершенствования технологии очистки выполняются теоретические и экспериментальные исследования [1], [8], [9], [10], [11], [17]. Экспериментальные исследования функционирования корообдирочных барабанов в реальных производственных условиях возможны в весьма ограниченном диапазоне технологических характеристик. Поэтому все более важную роль по мере развития информационных технологий играют методы математического моделирования [15]. В данной области исследований конкретные примеры использования численных методов при моделировании технологического процесса очистки древесины в корообдирочном барабане приведены в статьях [4], [5], [6], [13], [14], [16].

Удаление коры происходит в процессе соударений балансов друг с другом и с корпусом ба

рабана при условии, что появляются силы, достаточные для преодоления ее сцепления с древесиной. В современных условиях для определения этих сил все большее распространение получает метод дискретных элементов [16], [17]. По причине относительной новизны этого метода не все аспекты его практического применения при моделировании технологического процесса очистки древесины в корообдирочном барабане исследованы достаточно подробно. Так, к числу наименее изученных относятся геометрические аспекты контактного взаимодействия древесины в корообдирочном барабане.

В данной статье рассматриваются вопросы определения величины и формы пятна контакта для различных положений соударяющихся балансов, поскольку именно они в первую очередь влияют на производительность и качество окорки древесины.

Корпус корообдирочного барабана (рис. 1) представляет собой цилиндр (1), внутренний диаметр которого равен D КБ, а длина – L КБ.

По внутренней поверхности цилиндра вдоль его оси расположены ножи (2) с шагом О н и окнами для удаления коры (3).

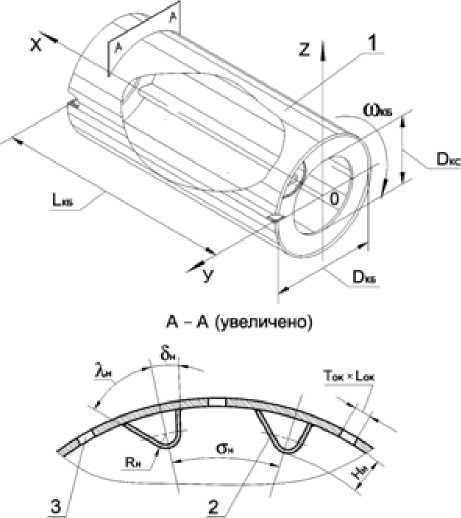
Рис. 1. Корпус корообдирочного барабана

Поверхность баланса в реальности представляет собой цилиндроид. Однако учитывая малую величину некруглости сечений баланса и небольшое расхождение между максимальным и минимальным диаметрами при математическом моделировании, каждый баланс можно рассматривать как прямой круговой цилиндр диаметром D Б и длиной L Б . При этом предполагаем, что масса древесины равномерно распределена по объему и баланс покрыт корой равномерной толщины t k (рис. 2).

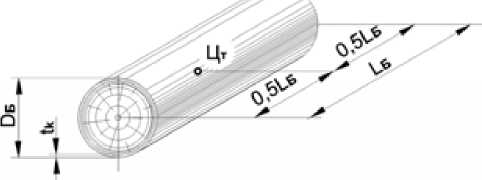
Рис. 2. Модель баланса

В объеме, ограниченном корпусом барабана, вращающегося со скоростью ю КБ , каждый баланс перемещается как тело, имеющее шесть степеней свободы. В каждый момент времени балансы занимают определенное положение относительно друг друга, а также относительно ножей и стенок барабана. Для определения положения балансов в данный момент времени введем систему координат, связанную с осью барабана (рис. 3).

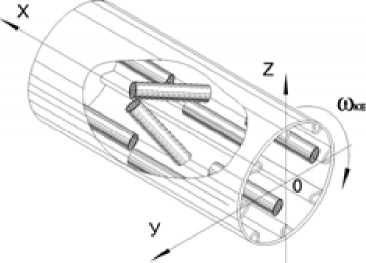
Рис. 3. Привязка системы координат к корообдирочному барабану

Положение i -го баланса в системе координат XУZ задаем центром тяжести Ц_Тi ( x_Цi y_Цi z_Цi ) и направлен и ем, которое определяется единичным вектором e_Бi или его координатами – косинусами углов, образованных заданным направлением с положительными направлениями осей координат (направляющие косинусы) (рис. 4).

tR = cos aR, mR = cos BG, nR = cos yG, (1) Б Б, Б Б, Б Б, где lБ - косинус угла наклона прямой к оси абсцисс (0x), mБ – косинус угла наклона прямой к оси ординат (0y), nБ – косинус угла наклона прямой к оси аппликат (0z), аБ - угол наклона прямой к оси абсцисс (0x), в Б - угол наклона прямой к оси ординат (0y), YБ - угол наклона прямой к оси аппликат (0z).

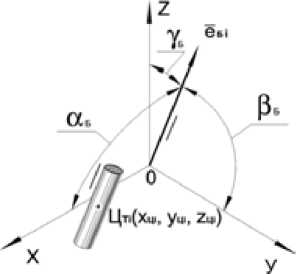
Рис. 4. Схема привязки баланса к принятой системе координат

Для определения пары соприкасающихся бревен надо перебрать все множество лесоматериалов, находящихся в барабане, на предмет определения кратчайшего расстояния между ними. Балансы будут соударяться, если это расстояние окажется меньше нуля. На первом этапе отбросим неперспективные на предмет соударения объекты. Соударения не будет, если расстояние между центрами тяжести бревен удовлетворяет условию:

^LБi + ^LБj + ^DБi + ^DБj

x Ц ^ХЦ)

>

где x_Цi , x_Цj – абсциссы центра тяжести i-го и j-го бревен; L_Бi , L_Бj –длины i-го и j-го бревен; D_Бi , D_Бj – диаметры i-го и j-го бревен.

На втором этапе определим кратчайшее расстояние между осями балансов ( 8 ) из выражения:

^ХЦ x j

± t_Bi

Бi

yji УЦ zji zUj mБi         nБi

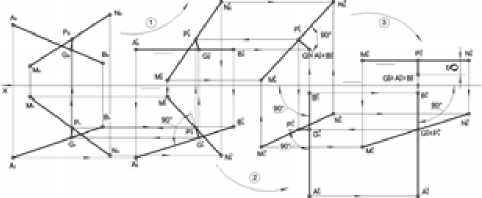
Рис. 6. Схема решения задачи методами геометрического моделирования

Бi

Бj

P

Бj

m Бj

n Бj

mБi

+

mБi

nБi

+

nБi

m Бj

m Бj

n Бj

n Бj

£K

Бi

Бj

где x Цi , x Цj , y Цi , y Цj , z Цi , z Цj – координаты центров тяжести i-го и j-го бревен; I _Бi , ^ б , m_Бi , ^тБ , n_Бi , п Б, — направляющие косинусы осей i-го и j-го бревен.

На третьем этапе отбросим все пары бревен, у которых величины 8 удовлетворяют условию:

DR, + Dr,

8> —--Б-

.

Для решения задачи плоскопараллельным переносом преобразуем модель так, чтобы баланс АВ занял положение, перпендикулярное фронтальной плоскости проекций, а MN – параллельное горизонтальной плоскости проекций (в принятой системе координат ось бревна АВ выродится в точку A 2 = B 2 ). За счет этого сложная задача построения перпендикуляра между двумя прямыми преобразуется в задачу простого измерения расстояния 8 . Недостаток этой методики заключается в том, что преобразования производятся в три этапа. С целью оптимизации процесса преобразования воспользуемся методами аналитической геометрии [7], [12].

И наконец, на четвертом этапе определим точки на осях балансов, соответствующие кратчайшему расстоянию. Эти точки будем называть точками скрещивания осей балансов. На рис. 5 показана геометрическая модель (чертеж) положения i-го и j-го бревен в пространстве. Отрезки AB и MN моделируют оси лесоматериалов. На рис. 6 приведена схема решения задачи по определению кратчайшего расстояния между отрезками методами геометрического моделирования [2], [3]. Отрезок прямой PG перпендикулярен осям AB и MN и поэтому является наименьшим расстоянием между ними.

Сначала произведем параллельный перенос начала координат в центр тяжести i-го баланса (рис. 7).

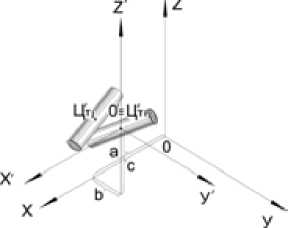
Рис. 7. Схема параллельного переноса начала координат в центр тяжести i-го баланса

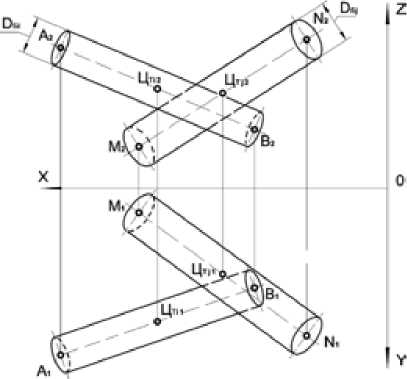
Рис. 5. Исходная геометрическая модель положения i-го и j-го бревен в пространстве

^ХЦ i = ⁰ , y Ц i = ⁰ , z Ц i = ⁰ .        ⁽⁵⁾

Новые координаты центра тяжести j-го баланса найдем из выражений:

^Х Ц, ^Х Ц a , У Ц,■ = Уц, ^- b , ^zj■ = z jj ^- c ,

где x_Цj , y_Цj , z_Цj – старые координаты центра тяжести j-го баланса; Х ц, ■ , У ц, ■ , Z j,■ - новые координаты центра тяжести j-го баланса; a = Х ц -величина переноса начала координат по оси 0x; b = У ц ,- - величина переноса начала координат по оси 0y; c = Z ji - величина переноса начала коор-

динат по оси 0z; x_Цi , y_Цi , z_Цi – старые координаты центра тяжести i-го баланса.

Направляющие косинусы i-го и j-го балансов после параллельного переноса останутся неизменными.

x	y	z
L Bi	m Б i	n Б i
£' Бj	m Б j	n Б j

= 0

.

^£ Bi = ^£ Ei , ^£ Ej ^£ Ej , m E i m b i , m Б j ⁼ m Б j , n Б i ⁼ n Б i , n Б j ⁼ n Б j .

Приведем выражение (10) к общему виду уравнения пло скости:

Затем произведем поворот осей координат так, чтобы ось ординат ( 0y ) совместилась с осью i-го бревна, а ось аппликат ( 0z ) стала перпендикулярна плоско сти σ , параллельной осям i-го и j-го балансов (рис. 8).

Ax + By + Cz = 0 ,          (11)

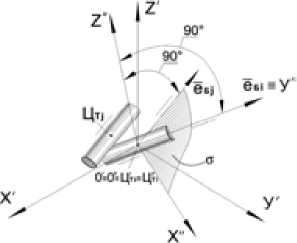
Рис. 8. Схема поворота осей координат

где

А – ( m_Б ′ _in_Б ′ _j - m_Б ′ _jn_Б ′ _i ) ,

В ^{- (} n Ei ^£ Ej — n Ej ^£ Ei ) ,

С ^{- ( £} Ei m Ej — ^£ Ej m Ei ) .

Уравнение прямой, проходящей через начало координат перпендикулярно плоскости σ , имеет вид:

x y z A ⁼ B ⁼ C ^.

С другой стороны, уравнение этой же прямой в канонической форме имеет вид:

Новые координаты центра тяжести j-го баланса получим из выражений:

^ХЦ = ^£ 1 ^ХЦ + m l y Ц + n 1 z m ,

У Ц = ^£ 2 ^Xj + m 2 У Ц ⁺ n 2 ^z ' ,        (8)

z m = ^£ з x m + m 3 ^уц + n з z m ,

x ₌ y ₌ z

£ 3 m 3 n ₃ .

Соответственно, направляющие косинусы оси 0 z , совпадающей с этой прямой, с учетом (11) будут равны:

где £ 1 - косинус новой оси x" относительно старой оси x' , £ 2 - косинус новой оси у относительно старой оси x , £ 3 - косинус новой оси z ′′ относительно старой оси x ′ , m ₁ – косинус новой оси x ′′ относительно старой оси y ′ , m ₂ – косинус новой оси y ′′ относительно старой оси y ′ , m ₃ – косинус новой оси z ′′ относительно старой оси y ′ , n ₁ – косинус новой оси x ′′ относительно старой оси z ′ , n ₂ – косинус новой оси y ′′ относительно старой оси z ′ , n 3 – косинус новой оси z ′′ относительно старой оси z ′ .

Определим величины направляющих косинусов новых осей координат относительно старых. Ось 0 y ′′ совпадает с осью i-го баланса, соответственно, направляющие косинусы этой оси с учетом (7) будут равны:

£з = (mEnE j - mE jnE^, m3 = (nE i£ E j - nE j£ Ei ) ,          (14)

n з = ^(£'з т ^Е] ^-£‘ зj m Ed.

Для нахождения направляющих косинусов оси 0 x используем определитель преобразования поворота Δ .

	£ 1	£ 2	£ з
Δ=	m 1	m 2	m 3
	n 1	n 2	n 3

^£ 2 = ^ Ei, m 2 = m Ei , n 2 = n Ei . ⁽⁹⁾

Ось 0 z ′′ перпендикулярна плоскости σ , параллельной осям i-го и j-го бревен. Выражение, задающее подобную плоскость σ , проходящую через начало координат, имеет вид:

Так как сумма квадратов элементов одной строки определителя Δ равна 1,

£2 + £22 + £2 = 1, m12+m22+m32=1 ,            (16)

n ₁ ² + n ₂ ² + n ₃ ² = 1 .

Преобразовав выражения (16), найдем направляющие косинусы оси 0 x ′′ .

t l = 7 1 - £ 22 - ^ ² 3 , m ₁ = 1 - m ₂ ² - m ₃ ² ,           (¹⁷)

n ₁ = 1 - n ₂ ² - n ₃ ² .

Новые направляющие косинусы j-го баланса получим из выражений:

^£ Бj = ^£ 1 ^£ Bj + m l m Bj + n 1 nB j , m j = £ ₂ t j + m ₂ m j + n ₂ n ‘ ,        (18)

n Bj = £ 3 ^ Бj + ^m 3 ^m Б j + n 3 ⁿ Б j .

Угол ϕ < 90 ° будем называть межосевым углом i-го и j-го балансов, он равен:

to = arccos £". , Бj

где £ ‘‘ j - косинус угла наклона прямой к оси абсцисс (0x) j-го баланса на преобразованной модели (рис. 9).

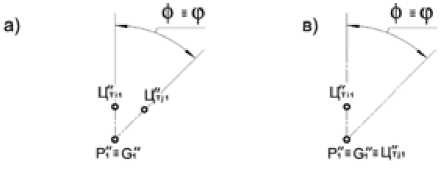
Угол соударения ( φ ) равен углу (рис. 10), вершиной которого является точка скрещивания осей балансов ( G ₁ ′′ , P ₁ ′′ ), а сторонами – направления на центры тяжести i-го и j-го балансов ( P ₁ ′′ Ц_Т ′ _i ′ ₁ и G ₁ ′′ Ц_Т ′ _j ′ ₁ ). В зависимости от взаимного положения точек контакта и центров тяжести балансов угол φ может быть острым ( φ ≤ 90 ° ) (рис. 10а) или тупым ( φ ≥ 90 ° ) (рис. 10б). Если один отрезок (рис. 10в) или оба (рис. 10г) вырождены ( P ₁ ′′≡ Ц_Т ′ _i ′ ₁ , G ₁ ′′≡ Ц_Т ′ _j ′ ₁ ), то указанный угол будет острым.

Геометрическая модель (рис. 5) после вышеперечисленных преобразований примет вид, приведенный на рис. 9. Точками скрещивания осей балансов являются точки P и G. Расстояния от центра тяжести баланса до точки скрещивания осей балансов ( L Цi и L Цj ) определим из выражений:

L_{Ц i} = | x_G - x_{Ц i} |,                 (19)

L Цj = ( x P - x Ц j )² + ( y P - y Ц j )²,     (20)

где L_{Ц i} – расстояние от центра тяжести i-го баланса до точки скрещивания осей балансов; L_{Ц j} – расстояние от центра тяжести j-го баланса до точки скрещивания осей балансов; x_G , x_{Ц i} , x_P , x_{Ц j} – координата х соответствующих точек: G , Ц_{Т i} , P , Ц_{Т j} ; y_G , y_{Ц i} , y_P , y_{Ц j} – координата y соответствующих точек: G , Ц_Т ′ _i , P , Ц_{Т j} .

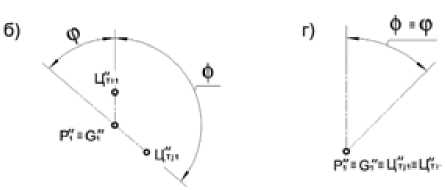
Рис. 10. Схема определения угла соударения

Если (( L_Цi - L_Цij ) ×( L_Цj - L_Цij )) < 0, то:

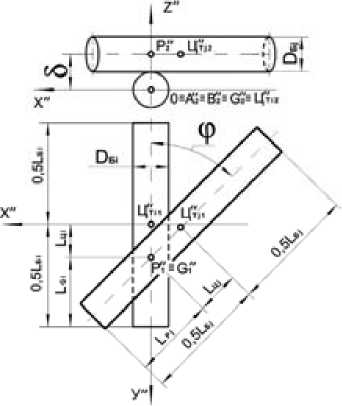
Рис. 9. Преобразованная геометрическая модель

φ = (180 ° - ϕ ) , иначе φ = ϕ ,         (22)

где L_Цij – расстояние между точками Ц_Т ′ _i ′ ₁ и Ц Т ′ j ′ 1 .

L_Цij = ( x_Ц ′′ _i - x_Ц ′′ _j ) + ( y_Ц ′′ _i - y_Ц ′′ _j ).        (23)

Расстояния от точки скрещивания осей балансов до ближних торцов i-го и j-го бревен определим по формулам:

L Gi = L Цi - 0,5 L Бi , L Pj = L Цj - 0,5 L Бj , (24)

где L_Gi – расстояния от точки скрещивания осей балансов до ближнего торца i-го баланса, L_Рj – расстояния от точки скрещивания осей балансов до ближнего торца j-го баланса, L_Бi – длина i-го баланса, L_Бj – длина j-го баланса.

Эти величины ( L_Gi и L_Рj ) положительны, если точки скрещивания осей балансов находятся между торцами балансов, и отрицательны, если снаружи.

L Gi >  0, если 0,5 L Б_i<  L^ , L_Pj >  0, если 0,5 L^ <  L_Ц| .

На рис. 11а, 11в, 11г изображены крайние положения пар соударяющихся балансов. Балансы не соприкоснутся, если

^L G, >  LKi или ^L Pj >  ^L Kj ,            (26)

где L_Кi , L_Кj – максимальные расстояния от торцов i-го и j-го балансов до точки их скрещивания ( Р "= G " ), при которых возможно соударение.

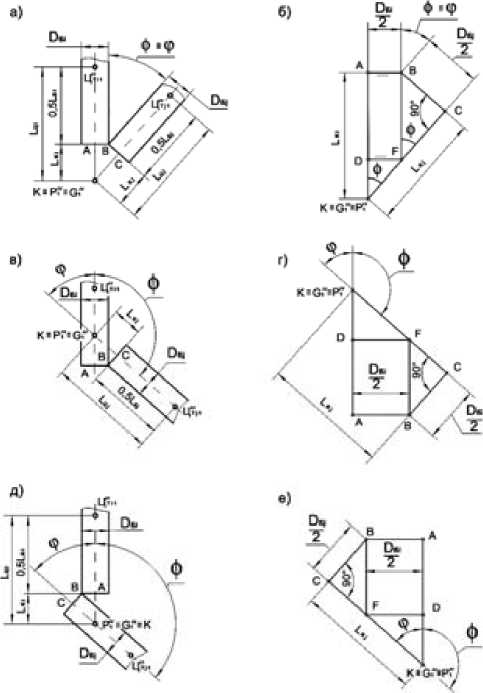
Рис. 11. Схемы крайних положений пар соударяющихся балансов

L_Ki = -Б^- + ^j , L_Kj = D^ ₊ J^ . (27) 2sin ф 2 tg ф        2 tg ф 2sin ф

Далее отбросим пары балансов, у которых L_G или L_Рj отрицательны и больше вышеупомянутой величины:

^{( L} Gi <  ⁰ и ^L Gi >1 ^l k |) ^{или ( L} Pj <  ⁰ и ^L Pj >1 ^L K.i I^).

После того как пары балансов прошли через предварительный отбор, который заключается в отсеивании вариантов, удовлетворяющих условиям (4) и (28), рассмотрим возможные соударения балансов и условия их возникновения.

С геометрической точки зрения в процессе очистки древесины в корообдирочном барабане могут иметь место следующие случаи взаимодействия пары балансов.

• 1.    Боковая поверхность баланса – боковая поверхность баланса.

  • 1.1.    Пятно контакта в форме эллипса или его части (рис. 12).

  • 1.2.    Пятно контакта в форме прямоугольника (рис. 13).

• 2.    Боковая поверхность баланса – ребро торцевой поверхности баланса (рис. 14).

• 3.    Торцевая поверхность баланса – ребро торцевой поверхности баланса (рис. 15).

• 4.    Ребро торцевой поверхности баланса – ребро торцевой поверхности баланса (рис. 16).

• 5.    Торцевая поверхность баланса – торцевая поверхность баланса (рис. 17).

Очевидно, что перечисленные виды технологических ситуаций не в полной мере описывают поведение балансов в барабане. Необходимо учесть и соударение балансов с элементами корпуса корообдирочного барабана, так как особенности формы этих элементов могут существенно затруднить моделирование. Однако и в этих случаях возможно использование предложенной методики для геометрического моделирования при соответствующей ее доработке. Поскольку рассмотрение появляющихся в этой связи вопросов выходит за рамки данной работы, мы предполагаем посвятить им отдельную статью.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 08-08-00979.

Для определения величин L_Кi и L_Кj воспользуемся схемами, приведенными на рис. 11б, 11г, 11д. Учитывая равенство отрезков AD и FB, а также то, что L_Ki = KD + AD и L_Kj = KF + Cf (величины отрезков FC и FB найдем из треугольника FBC, отрезков KD и KF – из треугольника KDF), получим:

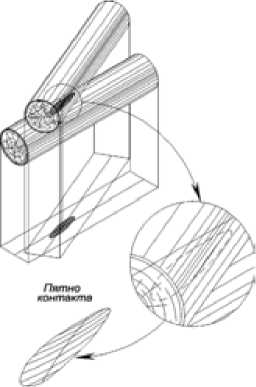
Рис. 12. Соударение пары балансов боковыми поверхностями с образованием пятна контакта эллиптической формы

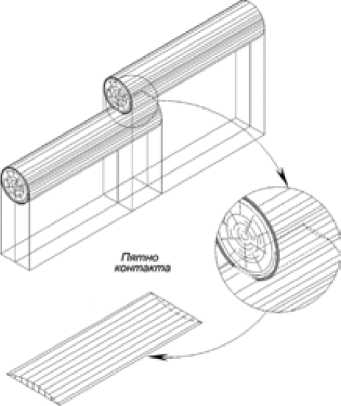
Рис. 13. Соударение пары балансов боковыми поверхностями с образованием пятна контакта прямоугольной формы

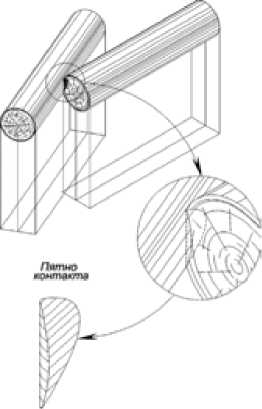
Рис. 14. Соударение пары балансов боковой поверхностью и ребром торцевой поверхности

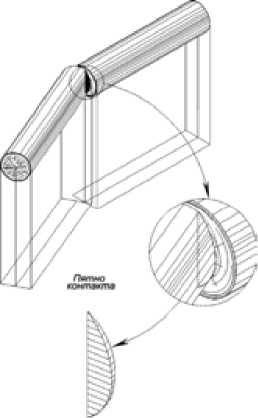
Рис. 15. Соударение пары балансов торцевой поверхностью и ребром торцевой поверхности

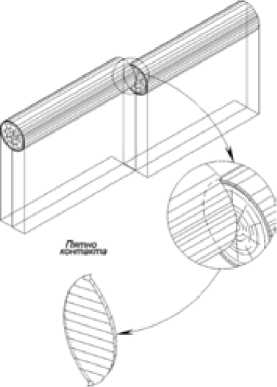
Рис. 16. Соударение пары балансов ребрами торцевых поверхностей

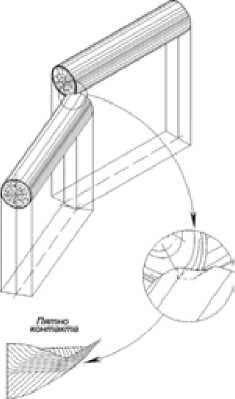
Рис. 17. Соударение пары балансов торцевыми поверхностями