Геометрические параметры и погрешности реальной геометрии недеформируемых деталей машиностроения

• 1.    Исходные понятия и определения в формировании представлений о параметрах геометрии деталей изделий машиностроения

Объектами машиностроения1 являются физические тела. Изделия машиностроения представляют собой результат сборки2 совокупности деталей3, являющихся наименьшими частями машин.

Геометрия деталей в машиностроении играет определяющую роль. Она пронизывает все стадии и этапы жизненного цикла изделия.

Деталь – тело , ограниченное от окружающей конечным множеством поверхностей⁴ разной величины ⁵, размеров ⁶ и формы ⁷. Поверхности и их расположение в системе координат⁸ ограничивают объем ⁹ деталей. Поверхности детали пересекаются или сопрягаются по рёбрам или линиям сопряжения . В местах пересечения более чем двух поверхностей, а также двух линий пересечения или сопряжения между ними образуются точки пересечения. Поверхность является первичным геометрическим элементом ¹⁰ конструкции детали. Основные поверхности деталей взаимодействуют с окружающей средой. По соприкасающимся поверхностям деталей осуществляется сборка деталей друг с другом. Часть поверхностей детали (фаски и скругления на границах пересечения основных поверхностей) носит вспомогательный характер.

Геометрические элементы детали могут быть:

• -    несимметричными (их больше) и симметричными с осевой или центральной симметрией (их меньше);

• -    с кривизной (их бесконечно большое количество) и без кривизны (это прямая линия и плоскость).

Замысел геометрии деталей, как и всякого другого элемента конструкции, рождается в номинальной геометрии поверхностей11, заданных в собственных системах координат поверхностей12 и представляемых в системе координат проекта13. Геометрию замысла называют номинальной геометрией детали14. Геометрические параметры формы номинальных поверхностей зависят от способа образования поверхностей: кинематического или каркасного (линейного или точечного) с последующим двумерным интерполированием формы номинальных поверхностей [1]. В общем случае большинство возможных форм номинальных поверхностей не имеет наименований. Их относят к поверхностям общего вида. Некоторые формы поверхностей с кривизной имеют определённые названия: конические, параболические, гиперболические, спиральные, торовые, и т.д. Поверхность без кривизны одна – плоскость. Геометрические параметры величины, формы и расположения номинальных поверхностей, определяемые характерными размерами15 длин и углов, единственные, поскольку номинальная величина и её размеры заданы в технической документации и могут быть больше или меньше только в пределах полей допусков16, обеспечивающих гарантированную собираемость17 и работоспособность18 машин.

Реальную геометрию¹⁹ поверхности детали получают после изготовления из заготовок ²⁰ по выбранному технологическому процессу ²¹ на выбранном оборудовани и²² с помощью выбранных средств технологического оснащения (СТО): инструментов ²³ , технологической оснастки ²⁴ , приспособлений ²⁵ .

Реальная геометрия детали отличается от номинальной геометрии. Отличие реальной геометрии поверхностей детали от номинальной геометрии состоит в отклонении параметров величины, формы и расположения реальных поверхностей детали от величины, формы и расположения номинальных поверхностей в системе координат проекта. Реальную геометрию детали измеряют выбранными средствами измерения ²⁶ .

Опираясь на результаты двухточечных измерений без указания системы координат, в которой проводятся измерения, однозначно определить насколько изготовленная деталь отличается от той, что была в проекте, не представляется возможным. Характерные размеры поверхностей и геометрические параметры отклонений формы и расположения реальных поверхностей оценивают по весьма приблизительным рекомендациям [2] и определяют в соответствии с несовершенными установленными правилами [3, 4].

Рассматривать всю деталь как целое и сравнивать геометрию реальной детали с номинальной геометрией детали можно, но неэффективно. Если рассматривать элементы детали с привычных позиций назначения допустимых ограничений формы и расположения поверхностей, то переход от рассмотрения геометрии детали в целом к реальным поверхностям, ограничивающим объем детали, сулит большие перспективы при решении задач оптимизации ограничений допусков на традиционные отклонения формы и расположения поверхностей в конструкторской и технологической документации.

Наиболее полную и достоверную информацию о реальной геометрии детали можно получить с помощью 3D координатно-измерительных машин ²⁷ (КИМ). Эти машины позволяют определить массивы координат точек, принадлежащих реальным поверхностям детали в системе координат системы измерения ²⁸ либо «ощупыванием» реальных поверхностей деталей, либо определением координаты точек тех же поверхностей лазерным интерферометром по времени пролёта луча света от источника излучения до контролируемой поверхности.

После точного измерения координат точек реальных поверхностей недеформируемой детали ²⁹, в системе координат системы измерения можно установить отличие геометрических параметров реальных поверхностей детали от геометрических параметров номинальной детали, представленной в системе координат проекта и сохранённой в памяти системы обработки информации 3D моделью номинальной геометрии детали.

Для определения отклонения формы собственную систему координат каждой из номинальных поверхностей, представленных номинальными поверхностями в системе координат проекта , нужно расположить в системе координат системы измерения таким образом, чтобы отклонение точек реальной геометрии поверхностей, представленных в системе координат системы измерения, определялось по нормали к номинальной геометрии .

Математическая модель определения отличия отклонений величины, расположения и формы реальной поверхности от номинальной геометрии зависит от выбора отсчётного элемента ³⁰ (линии или поверхности).

В стандарте [3] для всех отклонений формы и расположения, принятых к обязательному использованию в качестве отсчётных элементов используются прилегающие элементы³¹ , имеющие форму номинальных элементов, соприкасающихся с реальными элементами и расположенные вне материала детали так, чтобы максимальное отклонение Е max прилегающих элементов от наиболее удаленной точки реальных элементов имело минимальное значение ( Е max min ). Выбор прилегающих элементов в качестве отсчётных элементов не обеспечивает однозначного определения расположения номинальных элементов в системе координат системы измерения среди измеренных точек реальных элементов [5, 6] и не обеспечивает определения отклонения формы реальных элементов от номинальных. Тем не менее, вся существующая нормативная база для определения отклонений формы и расположения построена на прилегающих элементах. Нормативная база на отклонение величины элементов отсутствует, поскольку по умолчанию предполагается, что она входит в отклонение формы элемента.

В том же стандарте [3] оценку отклонения формы реальных элементов допускается осуществлять с помощью отсчётных элементов, расположенных среди точек реальных поверхностей по условию n

• ² min , характерному для средних элементов ³².

i 1

Если величина среднего элемента равна величине номинального элемента, то система координат реального элемента в системе координат системы измерения совпадает с системой координат номинального элемента, а отклонение точек реального элемента определяется по нормали к номинальному элементу. Для оценки расположения системы координат геометрического элемента среди случайных координат точек реальных геометрических элементов, измеренных в системе координат системы измерения, может быть использован аппарат ортогональной регрессии [7, 8].

Так, например, массиву измеренных точек, принадлежащих геометрическому элементу без кривизны , «похожему» на плоскость, в системе координат системы измерения соответствует плоскость ортогональной регрессии. Она находится внутри массива измеренных точек, проходит через центр тяжести массива, имеет вычисляемую нормаль к плоскости ортогональной регрессии [9], ориентирующую её в системе координат системы измерения. Для определения положения системы координат плоскости ортогональной регрессии в системе координат системы измерения необходимы направление нормали а к плоскости ортогональной регрессии, координаты двух точек принадлежащих реальной поверхности «похожей на плоскость». Направление третьей оси определяется исходя из условия ортогональности осей координат.

Для реального элемента с кривизной , имеющему номинальную форму и величину, в соответствии с определением понятия «средний элемент», положение собственной системы координат реального элемента среди массива точек, принадлежащих реальному элементу детали в системе координат системы измерения, всегда выполняется для несимметричных элементов [5. 6].

Для элементов с осевой симметрией положение оси симметрии номинального элемента (поверхности), определяется однозначно также по тому же условию. Начало собственной системы координат реальной поверхности связано с точкой на оси симметрии, положение первой оси системы координат совпадает с направлением оси. Положение второй оси собственной системы координат реального элемента определяется по измерению в системе координат системы измерения координат реперной точки, принадлежащей реальному элементу, «похожему на поверхность вращения. Это предотвращает возможный произвольный поворот системы координат реального элемента вокруг оси симметрии, приводящий к неопределённости положения собственной системы координат реального элемента. Направление третьей оси определяется исходя из условия ортогональности осей координат.

Для элемента с центральной симметрией (сфера) положение центра симметрии номинального элемента (поверхности) в системе координат системы измерения среди измеренных точек реальной поверхности определяется однозначно также по условию определения положения «среднего элемента». Предотвращение произвольного поворота системы координат номинального элемента вокруг оси симметрии, приводящего к неопределённости положения системы координат реального элемента, обеспечивается координированием двух точек (реперов) и измерении их координат на реальном номинальном элементе в системе координат системы измерения.

А что делать, если величина реального несимметричного элемента с кривизной отличается от величины номинального?

Прежде всего, нужно сохранить положение системы координат несимметричного номинального элемента в системе координат системы измерения, необходимое для определения отклонения формы. При изменении величины несимметричного реального элемента сохранение системы координат номинального элемента в системе координат системы измерения возможно только для эквидистанты³³ к номинальному элементу или изменённого масштаба номинального элемента в собственной системе координат номинального элемента [10]. Неопределённость термина форма элемента допускает такую замену для номинальной формы элемента.

Системы координат эквидистанты к номинальному элементу и изменённого масштаба в собственной системе координат несимметричного номинального элемента в системе координат проекта номинального элемента совпадают с собственной системой координат номинального элемента. Собственные системы координат номинального элемента и масштабированного относительно начала собственной системы координат также совпадают. Положение собственной системы координат масштабированного элемента в системе координат системы измерения позволяет определить его расположение относительно определяемых таким же способом систем координат других реальных элементов.

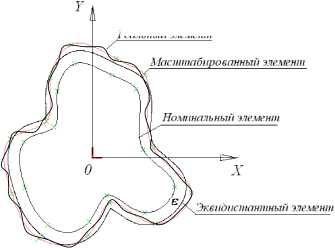
Сравнение двух способов сохранения положения систем координат номинального элемента с эквидистантным и масштабированным элементами представлено на рис. 1.

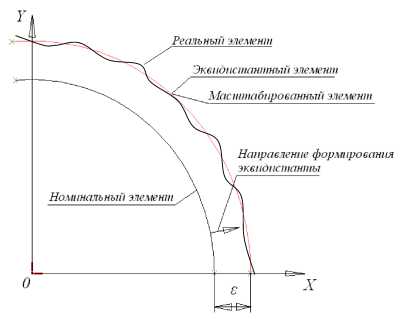
Рис. 1. К сравнению сохранения положения системы координат номинального элемента в системе координат системы измерения: а – для дуги, б – для замкнутого контура, ограниченного циклическим сплайном

Реальные! элемент

б

Изменяя направление формирования эквидистанты по одну или другую сторону от несимметричного номинального элемента и величину смещения 8 (рис. 1, а ), можно подобрать их такими, чтобы после поворота и перемещения собственной системы координат сформированного отсчётного элемента в системе координат системы измерения, был обеспечен минимум суммы квадратов отклонений точек реальной поверхности от отсчётной. Такую эквидистанту называют отсчётной эквидистантой [5, 6] . Форма отсчётной эквидистанты требует достаточно громоздкой процедуры построения эквидистанты и приводит к большим отличиям формы поверхности при больших 8 и номинальных сплайновых элементах. Поэтому она имеет область применения, ограниченную геометрическими элементами вращения: линии (круги, дуги) и поверхности с линейной или круговой образующей.

Изменяя масштаб номинальной поверхности в собственной системе координат номинальной поверхности можно подобрать его величину такой, чтобы после поворота и перемещения собственной системы координат сформированной отсчётного элемента (поверхности) в системе координат системы измерения, был обеспечен минимум суммы квадратов отклонения точек реальной поверхности от отсчётной (рис. 1, б ). В дальнейшем будем называть такой элемент отсчётным ортогональным элементом.

Отсчётные ортогональные элементы, имеют форму номинального элемента и такую величину и расположение, что сумма квадратов расстояний между реальным и средним элементами в пределах нормируемого участка имеет минимальное значение. Достаточная величина отсчётного ортогонального элемента достигается масштабированием номинальной поверхности детали до необходимой величины. Форма такого отсчётного ортогонального элемента сохраняется при любом масштабировании любого несимметричного и с любой симметрией номинального элемента при сохранении параметров масштабирования по каждой из осей X, Y, Z.

Перемещая начало координат и поворачивая собственную систему координат масштабируемого номинального элемента в системе координат системы измерения, определяем положение его собственной системы координат и размер масштаба, которому соответствует наименьшая сумма квадратов отклонений точек реального элемента от масштабируемого. Найденная величина масштабирования номинального элемента определяет величину реального геометрического элемента. Расположение системы координат реальной поверхности в системе координат системы измерения определяется координатами начала системы координат (точки Oр с координатами Xр, Yр. Zр) и матрицей Ар положения осей собственной системы координат реальной поверхности, определённой по положению отсчётной ортогональной поверхности среди точек реальной поверхности.

Взаимное расположение систем координат можно определить с помощью универсальных геом

X 0 '

X1

X0

O

Z 0 ’

Y 1

Z1

R ₁₀

Z0Y0

Рис. 2. Универсальные геометрические параметры

Положение точки начала отсчета О 1 системы координат О 1 X 1 Y 1 Z 1 в системе координат системы измерения О 0 X 0 Y 0 Z 0 задаётся модулем радиус-вектора R 10 и двумя углами co иф сферической системы координат или проекциями радиус-вектора R 10 X О1 , Y О1 , Z О1 . Направление осей системы координат О 1 X 1 Y 1 Z 1 в системе координат О 1 X 0 Y 0 Z 0 , параллельной предыдущей, задаётся: углом «перекоса» ОС оси X 1 относительно оси X 0 , углом направления перекоса р между осью Y 0 системы координат X 0 Y 0 Z 0 , параллельной X 0 Y 0 Z 0 и проекцией оси X 1 на плоскость ( X 0 Y 0 ), углом у «закрутки» между осью Y 0 базовой системы координат X 0 Y 0 Z 0 и проекцией оси Y 1 на плоскость ( X 0 Y 0 ). Углы ос и со отсчитываются от положительного направления оси X 0 , соответственно, и изменяются в пределах от 0 до 7Г . Углы Ф,Риу отсчитываются в направлении против часовой стрелки от оси Y 0 к проекциям вектора R и осей X 1 , Y 1 , соответственно, и изменяются в интервале от 0 до 27Г .

Переход от измеряемых УГП к векторно-матричным параметрам R 10 и А 10 в декартовой системе координат выполняется по соотношениям:

R ₁₀

^XO 1

Y_{O 1}

и A ₁₀

l

m

n

l ₂

l ₃

m n2

m ₃

n ₃

где: X О1, Y О1, Z О1 – декартовы координаты точки начала отсчета CK X1 Y1 Z1, li, mi, ni – элементы матрицы A10 направляющих косинусов осей X1, Y1, Z1 относительно осей X0,Y0, Z0

Из геометрических построений следует:

l 1 = cos у/ K , m 1 = sin у/ K , n 1 = – K 1 / K ,

l2 = m3 n1 – m1

m2 = n3 l1 – l3

n2 = l3  m1 – l1

l3 = sin ос • cos р, m3 = sin ос • sin р, n3 = cos ОС ,

K = [1 + K12 ]0.5,K1 = tg ос • cos(р–у).

Обратный переход из векторно-матричной формы к УГП выполняется по соотношениям:

Ri =  XО24i   YО24i   ZО24i , i = arccos

(          XО4i)

2          22

О4i     О4iО i= arctg (ZO4i/YO4i), i = arccos n3i, i = arctg (m3i/l3i), i = arctg (m1i/l1i).

В системе координат системы измерения можно получить расположение собственных координат всех реальных поверхностей детали. Для того, чтобы сравнить отклонение (разницу) расположения систем координат номинальных и реальных поверхностей необходимо произвести базировани е³⁴ в выбранной системе координат ³⁵ . Такой системой координат будет система координат базы ³⁶ , одинаковая для систем координат проекта и системы координат системы измерения.

Расположение реальной поверхности в системе координат базы можно представить как сумму расположения номинальной поверхности, представляемой вектором R Н и матрицей А Н и погрешности расположения [5, 9], представляемой вектором R РН и матрицей поворота А РН :

R РН = A ^Т Н ( R Р – R Н ),

AРН = AТН AР, где AТН – транспонированная матрица AН.

Положение точки начала отсчета О н номинальной системы координат О н X н Y н Z н в системе координат базы О Б X Б Y Б Z Б задают вектором R Н.. Положение точки начала отсчета О Р реальной системы координат О Р X Р Y Р Z Р в системе координат базы О Б X Б Y Б Z Б задают вектором R Р .

Отклонение расположения R РН определяется по отклонению расположения начала О Р системы координат реального рассматриваемого элемента от начала О Н системы координат номинального элемента в системе координат O Б X Б Y Б Z Б , принятой за базу в системах координат номинальной и реальной геометрии . Его вычисляют по формулам:

(RР – RН) = xOр xOн yOр yOн zOр zOн в направлении AТН, определяемом направляющими косинусами lРН,mРН,nРН,

l 1 н    m 1 н    n 1 н A Т Н = l 2 н   m 2 н   n 2 н l 3 н   m 3 н   n 3 н

l 1 н       l 2 н       l 3 н – транспонированная матрица A Н = m   m    m   . nnn н        н       3 н

Поворот системы координат OPXPYPZP относительно системы координат ОНХН YdZH, определяется матрицей поворота АРрн = AТн • Aр, где:

	l 1 н	m 1 н	n 1 н		l 1 н	l 2 н	l 3 н
A Т Н =	l 2 н	m 2 н	n 2 н	– транспонированная матрица A Н =	m 1 н	m 2 н	m 3 н
	l 3 н	m 3 н	n 3 н		n 1 н	n 2 н	n 3 н

Ар = l1н l1 р m1р n1р m1н /7 2р L - 3р m3р n3р l1 р . к 2р к " 3р m2р n2р n1н АРН = l2н m2н n2н m1р m2р m3р l3н m3н n3н n1р n2р n3р l1нl1р + m1нm1р +n1н n1 р l1н l2 р + m1нm2р +n1н n2р l1нl3р + m1нm3р +n1нn3р

• ^l 2р ^l 1р + ^m 2н ^m 1 р +n 2н n 1 р l 2р l 2 р + ^m 2н ^m 2 р +n 2н n 2 р l 2р l 3 р + ^m 2н ^m 3 р +ⁿ 2н ⁿ 3 р l 3н l 1р + ^m 3н ^m 1 р +n 3н n 1 р l 3н l 2 р + ^m 3н ^m 2 р +n 3н n 2 р l 3н l 3 р + ^m 3н ^m 3 р +ⁿ 3н ⁿ 3 р

Отклонение формы реальных элементов определяется по отклонениям точек реальных элементов от номинальных элементов. Отсчётным элементом для определения отклонения формы можно считать геометрию номинального элемента .

К отсчётным поверхностям построим эквидистанты нижней и верхней границ предельных отклонений формы по обе стороны отсчётной поверхности. Назовём эти эквидистанты эквивалентными поверхностями. Положение эквивалентных поверхностей ограничивают коридор отклонения точек реальной поверхности от формы номинальной поверхности, включающий совместное действие волнистости³⁷ и шероховатости³⁸. Эквивалентные поверхности, которым соответствует максимум материала детали, охватывают тело детали по предельным отклонениям реальных поверхностей и ограничивают объём, величина которого превосходит объём, ограниченный реальной поверхностью детали. Назовём их эквивалентами реальных поверхностей . Они представляют собой некоторое подобие прилегающих поверхностей [3], имеют форму номинальной поверхности, величина и расположение систем координат в системе координат системы измерения соответствуют расположению реальных поверхностей. Точки пересечения собственных систем координат реальных поверхностей с эквивалентами реальных поверхностей детали, могут быть использованы для определения характерных размеров детали.

Для одной детали эквиваленты реальных поверхностей детерминированы39, однозначны. Имеют форму номинальных поверхностей, величину близкую к величине номинальных поверхностей и расположение собственных систем координат реальных поверхностей по направлениям, совпадающим с направлениями отсчётных ортогональных поверхностей в системе координат системы измерения. Они зависят от технологии (последовательности действий) и применявшихся СТО. Для множества деталей, имеющих одну и ту же номинальную геометрию, но изготовленные по различным технологиям, использующим различные СТО, эквивалентные поверхности и все геометрические параметры деталей случайны. Случайные величины характеризуются набором статистических параметров, среди которых диапазон рассеивания или размах, математическое ожидание, дисперсия, закон распределения, доверительная вероятность и т. п. Поэтому статистика эквивалентных поверхностей отражает каждую технологию и состав применяемых СТО.

Таким образом, для реальной недеформируемой детали после измерения координат точек реальных геометрических элементов и переноса всех измеренных координат точек в систему координат системы измерения, метод, предложенный в данной статье, позволяет однозначно определить вычислением:

• -    величину реально получившихся геометрических элементов;

• -    положение систем координат реальных геометрических элементов в системе координат системы измерения;

• -    отклонения расположения реальных геометрических элементов в системе координат системы измерения от их расположения в системе координат проекта;

• -    отклонения формы реальных геометрических элементов.

Для получения численных данных результатов измерений необходима разработка программноматематического обеспечения следующих вопросов:

• -    приведения результатов измерения координат точек реальных поверхностей со всех точек наблюдения в одну систему координат системы измерения;

• -    разработки системы вычисления геометрических параметров отклонений величины, расположения и формы реальных поверхностей детали.

• 2. Примеры определения величины и отклонений геометрических параметров реальных осесимметричных деталей

Детали в машиностроении разделяют на объемлемымые40 и объемлющие41.

Простейшими примерами являются: вал (рис. 3 а ) для объемлемой детали, втулка с отверстием⁴² (рис. 3 б) для объемлющей.

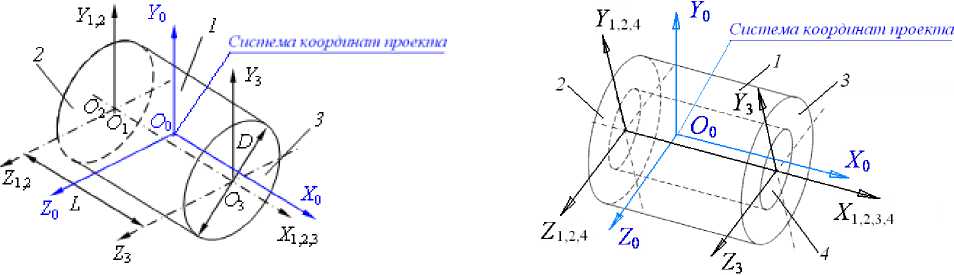
а                                                  б

Рис. 3. Номинальная геометрия деталей в системе координат проекта: а – вал, б – втулка с отверстием

Номинальный объём объемлемой детали – вала в системе координат проекта ограничен цилиндрической поверхностью 1 и двумя торцовыми плоскостями 2 и 3 (рис. 1 а ). Деталь с отверстием⁴³ является наиболее универсальным представителем объемлющей детали. Отверстие без детали не материально. В системе координат проекта вала появляется ещё одна поверхность – сквозное отверстие. Номинальный объём объемлющей детали – втулки – в системе координат проекта ограничен цилиндрической поверхностью 1 , двумя плоскостями 2 и 3 и сквозным отверстием 4 , превращающим вал во втулку (рис. 1 б ). При увеличении диаметра наружного цилиндра и числа отверстий втулка становится фланцем ⁴⁴. Но пока рассмотрим втулку как деталь с отверстием.

Изготовление вала по номинальному чертежу или номинальной 3D модели выбранными средствами технологического оснащения (СТО) и технологии даст деталь с реальными поверхностями.

В [10] описано определение состава всех геометрических параметров, определяющих отличие реальной геометрии от номинальной, и формирование элементов отчёта о геометрии простейшей объемлемой детали – вала.

Реальная геометрия детали, измеренная в системе координат системы измерения с помощью координатно-измерительных машин (КИМ) отличается от номинальной геометрии, представленной в системе координат проекта. Отличие состоит в отклонении величины , формы реальных поверхностей от величины и формы номинальных поверхностей, а так же расположении реальных поверхностей от расположения номинальных поверхностей в системе координат проекта .

В системе координат системы измерения отклонения величины, формы и расположения реальных поверхностей и отличие их от номинальной геометрии детали можно определить с помощью отсчётных ортогональных поверхностей .

В [10] доказано, что для поверхностей, которым в системе координат проекта соответствуют поверхности без кривизны (плоскости), отсчётными поверхностями реальных поверхностей торцов, «похожих на плоскости», являются плоскости ортогональной регрессии. Для реальной боковой поверхности с кривизной, «похожей на цилиндр», отсчётной ортогональной поверхностью является отсчётная эквидистанта или, что в данном случае одно и то же, масштабируемая номинальная поверхность. Величина поверхности, ограниченная отсчётной эквидистантой, соответствует величине реальной поверхности. По отношению к отсчётной эквидистанте или масштабируемой номинальной поверхности ортогональная регрессия обеспечивает однозначную привязку оси номинальной поверхности к системе координат системы измерения.

К отсчётным поверхностям ( отсчётной эквидистанте цилиндра или (что равноценно) отсчётного ортогонального элемента , а также к плоскостям ортогональной регрессии ) построим эквидистанты нижней и верхней границ предельных отклонений формы по обе стороны отсчётной поверхности (рис. 4).

Эквивалентный цилиндр

Реальная поверхность

Отсчётная эквидистанта

Границы коридора отклонения формы

Плоскость ортогональной регрессии

Направление нормалей к отсчётным плоскостям

Плоскость ортогональной регрессии

n 2

Реальная поверхность

O 3

Ось номинального и эквидистантного цилиндра

в+ экв

Реальная поверхность

Границы коридоров отклонения формы от отсчётных плоскостей

Эквивалентные плоскости

Рис. 4. Геометрические параметры реальной геометрии вала

Обозначим эквивалентные поверхности как для реальной поверхности, «похожей на цилиндр», имеющей диаметры D ^в снаружи тела детали и D ^в- внутри тела детали, так и реальных поверхностей, «похожих на плоскость», параллельные к плоскостям ортогональной регрессии, имеющие также отклонения снаружи тела детали H ^в и внутри тела H ^{в -} .

Эквивалент реального диаметра вала равен диаметру D ^в эквивалентной поверхности «похожей на цилиндр», который отличается от номинального диаметра D н в большую или меньшую сторону.

Определённое при обработке данных измерения положение и направление оси реальной поверхности, «похожей на цилиндр» пересекается с эквивалентами торцов, «похожих на плоскости» в точках О 2 и О 3 (см. рис. 4).

Эквивалент длины вала равен длине расстояния L рв между точками О 2 и О 3 , соответствующего точкам пересечения оси номинального цилиндра с эквивалентами реальных поверхностей торцов.

Отклонение точки реальной боковой поверхности вала от номинальной поверхности равно R ^бп – расстоянию от точки реальной поверхности, «похожей на цилиндр» до диаметра Dн номинального цилиндра по нормали к номинальной геометрии.

Отклонение формы реальной боковой поверхности вала от номинальной поверхности равно A R ^бп – расстоянию от эквивалентной поверхности, которому соответствует максимум материала детали до номинального цилиндра по нормали к номинальной геометрии. В терминах стандарта [3 (п. 2.4.1).] это соответствует наибольшему расстоянию EFZ⁴⁵ от точек реальной поверхности до прилегающего цилиндра в пределах нормируемого участка. В отклонение формы реальной боковой поверхности входят составляющие, связанные с отклонением величины и формы, обусловленные шероховатостью и волнистостью.

Отклонение точек торцовых поверхностей вала от номинальных поверхностей равно R ^тп – расстоянию от точек реальных поверхностей торцов «похожих на плоскость» до плоскостей ортогональной регрессии в системе координат системы измерения по нормали к ним.

Отклонение формы торцовых поверхностей вала от номинальной поверхности равно A _R тп – расстоянию от эквивалента торцовой поверхности, которому соответствует максимум материала детали до плоскостей ортогональной регрессии в системе координат системы измерения по нормали к ним. В терминах стандарта [3 (п. 2.2.1)] это соответствует наибольшему расстоянию ЕFЕ⁴⁶ от точек реальной поверхности до прилегающей плоскости в пределах нормируемого участка

Для привязки прямоугольной системы координат к поверхностям с осевой симметрией на поверхностях номинальной и реальной геометрии необходимо координировать направление и две точки (два репера). Такими направлением и точками на поверхности «похожей на цилиндр» являются: направление оси поверхности, точка О 1 , принадлежащая оси и точка k 1 , на эквиваленте реальной поверхности, «похожей на цилиндр». На поверхностях торцов «похожих на плоскости» направления нормалей к плоскостям ортогональной регрессии и точки О 2 , k 2 , О 3 и k 3 , принадлежащие эквивалентам торцов (рис. 5, а).

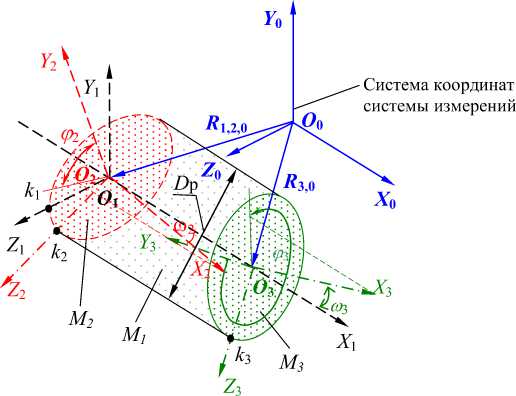
а

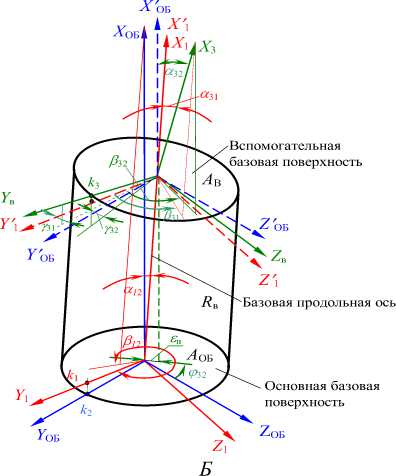
Рис. 5. Привязка систем координат к поверхностям с осевой симметрией и центральной симметрией

Системы координат поверхностей, «похожих на плоскости» можно сформировать и по реперным знакам, нанесённым на эквивалент реальной поверхности, «похожей на цилиндр» вблизи торцов. Тогда для формирования систем координат поверхностей детали, похожей на вал достаточно двух реперных знаков вблизи торцов на эквиваленте реальной поверхности, «похожей на цилиндр» (рис. 5, б ).

Отклонение расположения систем координат реальных элементов определяется в системе координат, принятой за базу⁴⁷ в системах координат проекта и системы измерения, по отличию расположения систем координат их реальных элементов от расположения систем координат номинальных элементов.

Если за базу принята система координат эквивалента реальной поверхности, «похожей на в цилиндр», имеющей диаметры D снаружи тела детали, то отклонения расположения нормалей к эквивалентам реальных поверхностей (плоскостей) торцов от направления оси поверхности, «похожей на цилиндр», определяется следующими параметрами УГП [9]:

• -    основная базовая поверхность параметрами R 21 = 0, и углами «перекоса» a 21 , оси X 1 относительно оси X ^’ 0 , углом направления перекоса р 21 и углом «закрутки» у²¹ = 0;

• -    вспомогательная базовая поверхность параметрами R 31 = L рв , ос 31 = 0, Р 31 = 0, у 31 = 0.

Углы между направлением оси цилиндра и нормалями к эквивалентам реальных поверхностей торцов определяют погрешности расположения торцов вала по отношению к реальной оси эквивалента реальной поверхности «похожей на цилиндр». В терминах стандарта [3 (п. 3.2.8)] это соответствует отклонению угла между осью поверхности вращения (прямой) и плоскостью от прямого угла (90°), что соответствует углу между осью эквивалентной поверхности и нормалью к эквивалентной поверхности торца, выраженное в линейных единицах ЕРR48 на длине нормируемого участка.

Если за базу принята система координат эквивалента реальной поверхности торца 2 «похожая на плоскость» (на рис. 4, б основная базовая поверхность), то отклонения расположения определяются следующими параметрами УГП [9]:

• -    эквивалента боковой поверхности «похожей на цилиндр» параметрами R 12 = 0, a 12 , P 12 .

• -    эквивалента вспомогательной базовой поверхности торца «похожего на плоскость» параметрами: R 32 = L рв , co 32 . Ф 32 , ОС 32 , p 32 , Y 32 .

Угла oc 32 недостаточно для однозначного определения понятия «отклонение от параллельности плоскостей». В это определение должны входить расстояние между плоскостями (в данном случае L 1рв на рис. 4, б ), направление наклона эквивалента реальной поверхности верхнего торца 3, определяемого углами co 32 и Ф 32 , а также направление нормали по отношению к системе координат торца 2, определяемого углами p 32 и Y 32 или смещением 8 32 проекции начала координат эквивалентной поверхности торца 3 на плоскость торца 2 в направлении, определяемом углом Ф 32 от оси Y системы координат основной базовой поверхности.

В терминах стандарта [3 (п. 3.1.1)] отклонение параллельности плоскостей по углу между направлениями нормалей к плоскостям отсутствует. Отклонение от параллельности плоскостей определяется как разность EРА49 наибольшего и наименьшего расстояний между плоскостями в пределах нормируемого участка.

Изменения таких геометрических параметров детали вал, как диаметр, длина, отклонение формы реальной боковой поверхности вала «похожей на цилиндр» и отклонение формы торцевых поверхностей вала, «похожих на плоскости» от номинальных поверхностей имеет одномерный характер. Такие свойства, как отклонение расположения нормалей к эквивалентным поверхностям (плоскостям) торцов от направления оси поверхности, «похожей на цилиндр» и отклонение от параллельности (непараллельность) торцов – трёхмерный характер (рис. 5 б ).

Перейдём к рассмотрению объемлющей детали. Наиболее универсальным представителем объемлющей детали является деталь с отверстием⁵⁰. Отверстие без детали не материально. В системе координат проекта вала введём ещё одну поверхность – сквозное отверстие 4, превратив вал во втулку (рис. 3 б ). Рассмотрим только геометрию сквозного отверстия.

Реальное сквозное отверстие будет иметь отклонения формы и расположения во втулке. Считая, что в системе координат системы измерения определены координаты всех точек реальной поверхности отверстия во втулке, применим к облакам точек реальных поверхностей приём, описанный ранее для цилиндрической поверхности вала.

Построим сначала отсчётные ортогональные элементы к наружной поверхности втулки, похожей на вал и внутренней поверхности втулки – отверстию, а затем эквиваленты реальных поверхностей , ограничивающие наибольший и наименьший объемы материала тела детали (втулки). Реальные границы детали проходят по всем эквивалентам реальных поверхностей (рис. 6).

Отсчётные ортогональные элементы

Эквивалентные поверхности отверстия и вала

Реальные поверхности

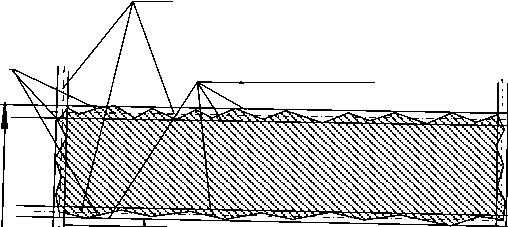
Направление нормалей к эквивалентным плоскостям d

D

n 1

d ^о+ экв

О ' 4

О 4

L ро

Эквивалентные поверхности торцов

Рис. 6. Геометрические параметры реальной геометрии втулки

n 2

Ось отверстия

Эквивалент диаметра реального отверстия равен диаметру d ^о эквивалентной поверхности реального отверстия «похожего на цилиндр», который отличается от номинального диаметра d н в большую или меньшую сторону.

Определённое при обработке данных измерения в системе координат системы измерения положение и направление оси реальной поверхности отверстия, «похожего на цилиндр», пересекается с эквивалентами реальных поверхностей торцов, «похожих на плоскости» в точках О 4 и О 4 .

Эквивалент длины реального сквозного отверстия равен длине расстояния L ро между точками О 4 и О 4 , соответствующее точкам пересечения оси номинального цилиндра с эквивалентами реальных поверхностей торцов.

Отклонение точки реальной боковой поверхности отверстия от номинальной поверхности равно R ^бп – расстоянию от точки реальной поверхности, «похожей на цилиндр» до диаметра d н номинального цилиндра по нормали к номинальной геометрии.

Отклонение формы реальной боковой поверхности отверстия от номинальной поверхности равно А R ^бп – расстоянию от эквивалента реальной поверхности до номинального цилиндра по нормали к номинальной геометрии.

Привязка номинальной геометрии поверхностей отверстий и торцов втулки к системе координат системы измерения осуществляется отсчётными ортогональными элементами к реальным поверхностям и торцам, «похожим на цилиндры и плоскости». Ортогональные отсчётные элементы обеспечивают минимум суммы квадратов отклонений точек реальной поверхности отверстий и торцов. Они определяют направление осей реальных поверхности отверстий, положения и направления нормалей ортогональных плоскостей.

Для формирования систем координат отсчётных плоскостей торцов, наружной поверхности вала и внутренней поверхности отверстия необходимы координаты двух точек и направления нормалей к плоскостям и осей цилиндрических поверхностей. Точки должны быть расположены на нормалях, осях и поверхностях. Они предотвращают возможный произвольный поворота отсчётных ортогональных элементов вокруг оси симметрии, приводящих к неопределённости положения номинальной системы координат по отношению к геометрии реального элемента. Это осуществляется указанием реперов на номинальной и измерением на реальной геометрии (точки k1,

k 2 , k 3 , k 4 ) в системах координат проекта и измерения (рис. 7).

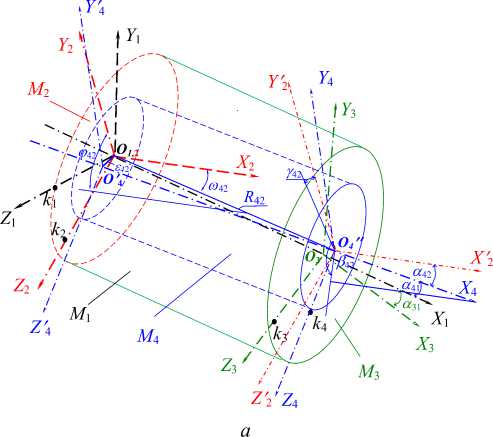
Рис. 7. Привязка систем координат к эквивалентам реальных элементов: а – с осевой симметрией и плоскостям с центральной симметрией для втулки;

б – к формированию системы координат отверстия во втулке

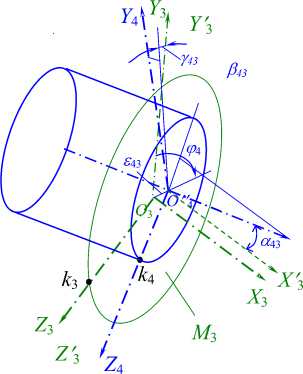
б

Ось отверстия проходит через точки О 4 и О 4 , ось наружной поверхности втулки через точки О 1 и О 3 , координаты которых можно вычислить в системе координат системы измерения при определении положения осей эквивалентов реальных поверхностей «похожих на цилиндры и плоскости». В самом общем случае оси наружной поверхности цилиндра втулки не параллельны и не пересекаются.

Если две оси (прямые) заданы каноническими уравнениями вида:

^{x  x} 1     ^{y  y} 1     ^z zx ^x 2     ^{y y} 2    ^{z z}

=        =        и        =        =, lmnlmn то косинус угла между ними можно найти по формуле:

cos ф

l ₁ l ₂ + m ₁ m ₂ + n ₁ n ₂

Il2   m2   n2 Il2   m22

l1   m1   n1 l2   m2

Угол между скрещивающимися осями определяется по известной формуле:

φ = arccos φ.

В терминах стандарта [3 (п. 3.3.4.)] отклонение наклона оси (или прямой) относительно оси ‘(прямой) или плоскости – отклонение угла (угол) между осью поверхности вращения (прямой) и базовой осью или базовой плоскостью от номинального угла, выраженное в линейных единицах ЕРR на длине нормируемого участка

Дополнительно следует рассмотреть условия параллельности и перпендикулярности: lmn

• -    условие параллельности осей (прямых): ¹ =  ¹ = ¹ ;

l ₂    m ₂    n ₂

• -    условие перпендикулярности осей (прямых): l l 4- m ₁ m ₂ 4- n n = 0.

Наименьшее расстояние между осями, номинально пересекающимися соответствует расстоянию 5 между скрещивающимися осями (прямыми) в координатах начал и концов отрезков по формуле:

xx l

m

l 2

m

mn

nl

z ₂    z ₁

n

n

lm

m ₂   n ₂

n ₂    l ₂

lm

В терминах стандарта [3 (п. 3.7.1) ] отклонение от пересечения осей обозначают ЕРХ51.

Все реальные поверхности формируются в технологическом процессе независимо. Направления части осей систем координат поверхностей «похожих» на тела вращения и плоскости определяются осями симметрии отсчётных ортогональных поверхностей и нормалями к плоскостям ортогональной регрессии. Оставшиеся оси ортогональны первой. Привязка одной из осей связана с выбором координат точки начала координат, назначением и измерением координат точки, принадлежащей соответствующей поверхности. Начало координат для тел, похожих на тела вращения и плоскости выбираются в точках пересечения осей вращения. По координатам измеренных точек строится вторая ось, а направление третьей определяется из условия ортогональности трёх осей.

Базирование отверстия во втулке можно осуществить либо в системе координат, связанной с эквивалентом реальной поверхности наружной поверхности втулки 1, «похожей на цилиндр», либо в системе координат, связанной с эквивалентом реальной поверхности торца 2, «похожего на плоскость», либо в системе координат, связанной с эквивалентом реальной поверхности торца 3, «похожего на плоскость». Предпочтительнее система координат поверхности торца 3 втулки со стороны начала формирования (сверления) отверстия. Точка пересечения оси отверстия с эквивалентом торца 3 не может быть измерена. Её координаты могут быть только вычислены

Базирование системы координат отверстия O 4 , X 4 , Y 4 , Z 4 в системе координат O 3 , X 3 , Y 3 , Z 3 эквивалента торцевой поверхности втулки 3 (рис. 7 б) может быть определено набором следующих геометрических параметров УГП [9] R =8 43 , CO 43 = 7Г/2, ф 43 , ОС 43 , р 43 , у 43 .

Для базирования отверстия с координатами O 4 , X 4 , Y 4 , Z 4 в системе координат O 2 , X 2 , Y 2 , Z 2 эквивалента торцевой поверхности втулки 2 (рис. 7, а ) необходимо определить точку параллельного переноса начала и системы координат эквивалента торца 2 для определения параметров УГП. Перенесём начало параллельной системы координат из точки О 1 в точку О 4 на расстояние R 42 . Результат базирования может быть определён набором следующих геометрических параметров УГП [9]: R = R 42 , со 42 , со 42 , ОС 42 , р 42 , Y 42 .

Заключение

В разделе 1 приведено описание способа определения всех геометрических параметров поверхностей реальной детали: величины, характерных размеров, отклонений формы и расположения через эквиваленты реальных поверхностей по координатам точек реальных деталей, измеренных в системе координат системы измерения с помощью координатно-измерительных машин. Там же представлен удобный способ представления отклонений расположения собственных систем координат эквивалентов поверхностей через универсальные геометрические параметры (УГП).

Вторая часть посвящена описанию геометрических параметров и полного состава отклонений величины, формы и расположения наиболее типовых осесимметричных деталей вала и втулки с отверстием. Рассмотрено базирование этих типовых деталей в разных выбранных системах координат. Сделано согласование полученных результатов с установленными стандартами нормами.