Геометрические параметры мгновенного очага деформации при полосовой шаговой прокатке обратным ходом

Проектирование технологии и оборудования

полосовой шаговой прокатки [1, 2], осуществляемой, пользуясь терминологией прокатки на станах ХПТ, обратным ходом, требует знания геометрических параметров мгновенного очага деформации. При получении зависимостей для расчета геометрических параметров мгновенного очага деформации применяем известные методы, основанные на использовании в качестве исходных данных параметров прокатных валков, принятии условия пересечения поверхности валков и конуса деформации при определении линии входа металла в валки с учетом линейного смещения металла, определяемого по «правилу Емельяненко», допущении, что линия выхода металла из валков находится в плоскости осей поворота валков. Для определения угла касания и площади контактной поверхности полосы с валками необходимо знать геометрические границы мгновенного очага деформации. Зависимости для определения координаты Z передней границы мгновенного очага деформации [3], с учетом особенностей шаговой прокатки обратным ходом имеют вид: - для условий прокатки калибрующим участком валков (рис. 1) ^Z-IMifXa cos 5-- р , r(Z>0/2-Z)2+e2-p2f

_Д^+^ _(^/2-z£+£-p^_ р        e(D0-2Z)      ’ U -для условий прокатки калибрующим и обжимным участками валков, а также только обжимным участком валков (рис. 2) JP2-(z-z0y +х0 COS < --- Р r(Z)0/2-Z)2+e2-p2f [    e(D0-2Z)    _ Р ^ + Хк (D0/2-Z^ + е -р р         e^D0-2Z)      • U Координата X линии входа металла в валки также определяется по формуле [3], учитывающей осбенности шаговой прокатки обратным ходом (рис. 3) (Z)0/2-Z)2+e2-p2 X = р arccos  ----7— --------+ 0 -2Z) /  [(D^/^-ZV 4-е2-п2!2

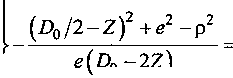
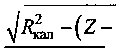
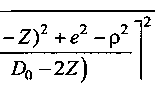
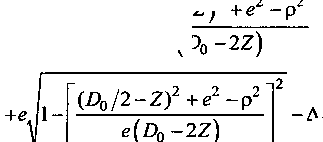
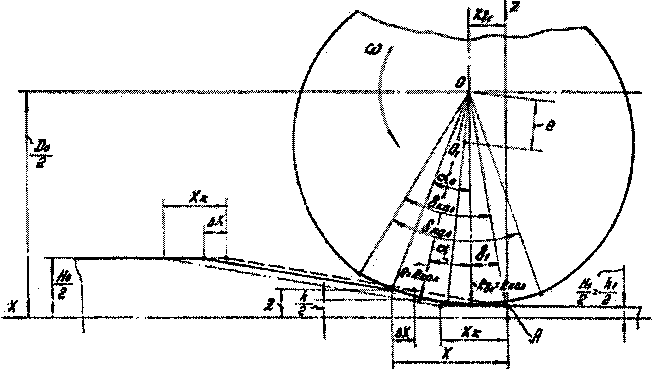
Рис. 1. Геометрия очага деформации при прокатке калибрующим участком валков

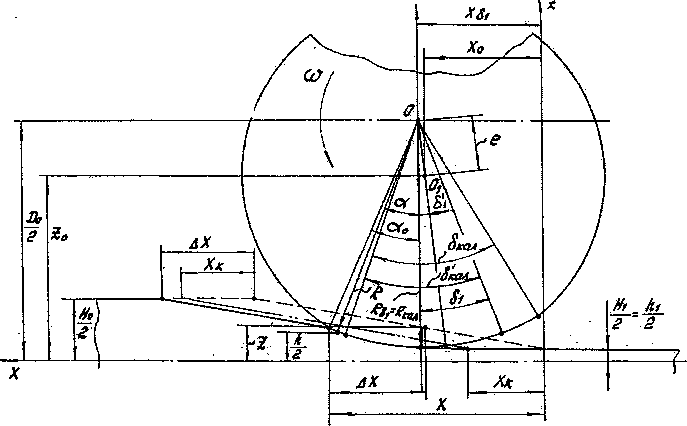
Рис. 2. Геометрия очага деформации при прокатке калибрующим и обжимным участками валков

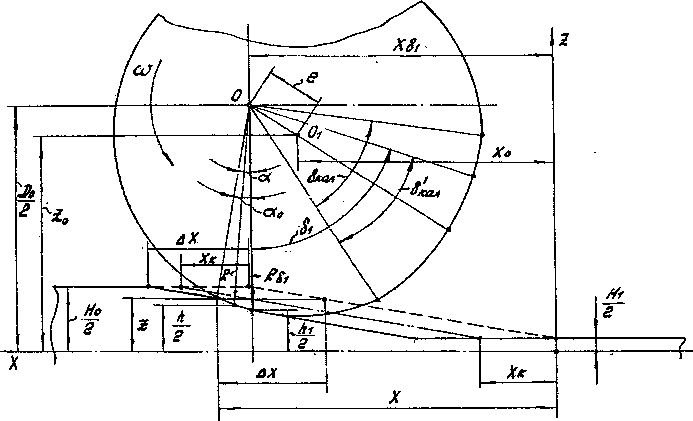
Рис. 3. Геометрия очага деформации при прокатке обжимным участком валков

Коваль Г.И., Фоменко В.В.

Геометрические параметры мгновенного очага деформации при полосовой шаговой прокатке обратным ходом

В зависимостях (1), (2), (3) обозначено: D_o -

расстояние между осями валков; р - радиус кри

визны обжимного участка; е - эксцентриситет обжимного участка; R_Kajl - радиус калибрующего участка.

Учитывая, что данные зависимости получены при начале отсчета угла поворота валков на линии ОО_Х, а фактически обжатие полосы начинается в точке А (см. рис. 1), следует связать координаты угла поворота валков 8_Т и 8}, характеризующие положение мгновенного очага деформации. Согласно рис. 2

§}=8i-(8L-5Kan/2).

очага деформации. Используя результаты экспериментальных исследований, принимаем линейный закон изменения ширины полосы по длине конуса деформации

^51 “^о + (А ~^о)

h8L-8KM/2) ’

Ширину исходной полосы В^ при заданном значении требуемой ширины готовой полосы В_х можно определить по формуле

Sq - В_х

А

Яо)

Угол 8^, характеризующий часть длины калибрующего участка валков, осуществляющего обжатие заготовки на конусе деформации, определяется по формуле

8кал “ ^^/ ^кал ’

где т - подача полосы; Л - вытяжка полосы.

Координаты центра кривизны обжимного участка валков в принятой системе координат равны

Х_й = Х_ъх -esinS},

где Я_о, Н_х- высота исходной и готовой полосы.

Показатель уширения с может быть определен экспериментально в зависимости от прокатываемого материала.

Центральный угол между серединой калибрующего участка и концом обжимного участка валков определяется по формуле [3]

8 сир

^-Н^² + 4е² -4р² = arccos--------------------

4еф„-Н^

Zo = D0/2-e cosSj.

Параметр X_k, характеризующий смещение начала обжимного участка валка от линии ОО_Ь определяется соотношением [3] при Z = HJ2

к

= р arccos

(туг-н^+^-р2 ^(£>0-2^)

Фо/г-я^+^-р² e^-lH^

С использованием зависимостей, определяющих геометрические границы мгновенного очага деформации с учетом результатов работы [4], получены формулы для расчета площади горизонтальной проекции поверхности контакта валков с полосой:

• -    при прокатке калибрующим участком валков

Fr = £§1otoFKajI,

• -    при прокатке одновременно калибрующим и обжимным участками валков

Ту -£§1

х

Положение задней границы мгновенного очага деформации определяется по следующим зави

l-^ao-SL-^)

симостям:

• - при прокатке калибрующим участком валка

^51 = ^кал81 ’

• -при прокатке калибрующим и обжимным участками валков, а также только обжимным участком валков

^61 = ^ал 8кал + Р ( 81 ~ 8кал ) +

■ve * sin 8j I 8_кал ^

-sin-^L

Угол касания [4]

^■-^81

a0 =arctg-;---;--2^.

• ^{0    6}(D₀/2-Z)

Боковая граница мгновенного очага деформации определяется шириной исходной полосы с учетом ее поперечной деформации. С достаточной степенью точности ширину полосы в пределах мгновенного очага деформации при полосовой шаговой прокатке принимаем постоянной и равной ширине полосы на выходе из мгновенного

При прокатке только обжимным участком валков

F_r = F₅₁F₅₁a₀ ^1 - К_х -у-

В принятой для определения геометрических параметров мгновенного очага деформации системе координат радиус рабочей поверхности валков определяется следующими соотношениями:

• -    на калибрующем участке

^51 = ^кал ’

• -    на обжимном участке

F₅₁ = д/р² -е² sin² 8} + е cos 8}.

Клиновидность валка, определяющая интенсивность изменения радиуса валка:

• -    на калибрующем участке при е=0

^ =0;

• -    на обжимном участке

esinS}

Кх — .......................................... ■.

д/ р -в sin о 1

При расчете кинематических и энергосиловых параметров необходимо знать высоту полосы h в пределах мгновенного очага деформации и высоту полосы на выходе из валков Н_х. Эти параметры находятся из следующих геометрических соотношений:

• -    при прокатке калибрующим участком валков

h = D₀ -2^ cos а,

= НХ)2;

• -    при прокатке обжимным участком валков к- D^- 27?_§1 (1 - ^а) cos а,

^ = Do - 2^51 •

В этих формулах угол а является произвольным углом в пределах мгновенного очага деформации.

Линейное смещение конуса деформации в сторону исходной полосы при деформации обжимным участком валков

^X = mX-NXx.

Величина NX_x , определяется по формуле, полученной с использованием результатов работы [5]

• -^ + xH₀m

Линейное смещение металла при деформации калибрующим участком валков принято изменяющимся по линейному закону

^кал

Линейное смещение в конце калибрующего участка АХК определяется по формуле (4) при 8i=5L-

Заключение. Для условий полосовой шаговой прокатки обратным ходом разработана методика расчета геометрических параметров мгновенного очага деформации.