Геометрические реализации неприводимых представлений групп вращений правильных многогранников в трехмерном пространстве

Автор: Зиза К.Н., Штепин В.В.

Журнал: Труды Московского физико-технического института @trudy-mipt

Рубрика: Оптимизация min-sum алгоритма декодирования LDPC-кодов

Статья в выпуске: 4 (32) т.8, 2016 года.

Бесплатный доступ

В работе найдены новые геометрические реализации неприводимых представлений групп вращений правильных многогранников в трехмерном пространстве. Предложена формула для проекционных операторов в каноническом разложении индуцированно- го представления, при помощи которой неприводимые представления реализуются в комплекснозначных функциях на вершинах, ребрах и гранях многогранников.

Группа, вращение, правильный многогранник, однородное пространство, индуцированное представление, неприводимое представление, спектр пред- ставления, реализация представления, оператор, проектор, базис

Короткий адрес: https://sciup.org/142186160

IDR: 142186160

Текст научной статьи Геометрические реализации неприводимых представлений групп вращений правильных многогранников в трехмерном пространстве

Настоящая работа посвящена построению явных реализаций неприводимых представлений групп вращений правильных многогранников в R ³ (а именно, групп A 4 , S 4 и A 5 )в функциях на однородных пространствах, связанных с многогранниками. Хотя правильные фигуры в R ³ известны еще со времен Платона и Евклида, а неприводимые представления их групп вращений — со времен Фробениуса (конец XIX века) [1, с. 49-51], задача построения реализаций неприводимых представлений все еще является актуальной.

В настоящее время известно несколько способов построения неприводимых представлений симметрической и знакопеременной группы. Метод Вейля позволяет строить реализации в тензорах определенного типа симметрии, в методе Яманучи неприводимые представления группы Sn строятся на основе представлений группы Sn-1. Еще на заре теории линейных представлений было известно, что регулярное представление конечной группы содержит в своем спектральном разложении все ее неприводимые комплексные представления с кратностями, равными их размерностям. Поэтому всякое неприводимое представление группы вращений многогранника может быть реализовано в комплекснозначных функциях на этой группе путем разложения кратного спектра ее регулярного представления. Хотя такая потенциальная возможность реализации представлений всегда имеется, ее практическое воплощение при увеличении порядка группы сталкивается с огромными вычислительными сложностями. Ниже мы предлагаем решение этой задачи более простым методом — путем реализации представлений в функциях на однородных пространствах.

Вероятно, начиная с классической работы Э. Картана [2, с. 217–252], берет свое начало направление, связанное с изучением однородных пространств и построением представлений в функциях на таких пространствах. Однородными пространствами, изучаемыми в данной работе, являются совокупности вершин, ребер и граней правильных многогранников в R ³ . Именно они, на наш взгляд, наиболее естественны для групп вращений и выгодно отличаются от остальных своей наглядностью и геометричностью.

Поскольку октаэдр двойственен кубу, а икосаэдр — додекаэдру, то достаточно ограничиться рассмотрением только тройки правильных многогранников в R ³ : тетраэдра, куба и додекаэдра. Для сопоставления вращений этих многогранников с подстановками у тетраэдра перенумеровываются вершины (его группа вращений изоморфна A 4 ), у куба – большие диагонали (группа вращений – S 4 ), у додекаэдра — отрезки, соединяющие противоположные вершины пары фиксированных противолежащих граней (группа вращений – A 5 ).

Пусть Ф - правильный многогранник с группой вращений G , а H p , Н / , H s - стационарная подгруппа какой-либо вершины, ребра или грани соответственно. Тогда однородное пространство вершин (ребер, граней) многогранника Ф можно понимать как множество левых смежных классов G по H _p ( G по H l , G по H _s ). Неподвижной вершине соответствует смежный класс, совпадающий с подгруппой H _p . Поэтому такую вершину удобно считать первой и обозначать p 1 . Аналогичное соглашение будем принимать также для ребер и граней.

Рассмотрим представление T p группы G , операторы которого действуют в пространстве комплекснозначных функций, определенных на однородном пространстве вершин многогранника Ф:

^[ T p ⁽ g ) f ^{] (} P i ) = f ( g ¹ P i ) • ⁽¹⁾

Мы докажем, что это представление является индуцированным тривиальным представлением E подгруппы H p , поэтому удобно обозначить его Ind H p E . Аналогично определяются представление Ind H E в случае однородного пространства ребер и Ind H s E в случае однородного пространства граней многогранника Ф.

Пусть G – конечная группа, T i — ее неприводимые комплексные представления с характерами x . ( i = 1 , 2 ,-.,r , где r — число классов сопряженных элементов в G ). Для произвольного конечномерного представления T группы G с характером χ T будем считать построенным каноническое разложение

T = ф m i T i ,

i =1

если вычислены кратности mi = TGGT 52 xt(g)Xi(g) (3)

|G| g∈G и найдены проекторы [3, с. 29

P i = t Gt Е X . ( s ) T ( 8 ) |G| _g _∈ _G

на подпространства примарных компонент m i T i . Отметим, что для индуцированного представления Ind H E формула для кратностей m i в каноническом разложении принимает следующий вид:

m i = THHT 52 X i ⁽ h ) , ⁽⁵⁾

|H| h∈H что является очевидным следствием теоремы двойственности Фробениуса [3, с. 55]. Если в каноническом разложении встречается хотя бы одна кратность больше 1, то спектр представления считается кратным. В противном случае говорят о представлении простого спектра.

В разделе 2 мы выводим новую формулу для проекторов P i на подпространства примар-ных компонент для индуцированных представлений типа Ind H E . Пусть примарное представление mT входит в спектральное разложение представления Ind H E . Тогда базисом в пространстве примарного представления служат столбцы проектора P i , соответствующие его наибольшему ненулевому симметричному минору. Действия операторов примарного и индуцированного представлений на векторах указанного базиса идентичны. Благодаря этому факту в работе найдены не только базисы в пространствах неприводимых представлений T i , но и матрицы операторов T i ( g j ) в этих базисах, где g j — образующие группы G .

Для придания геометрического смысла функциям из пространств неприводимых представлений (то есть для получения словесных описаний этих пространств) необходимо изобразить на многогранниках значения базисных функций, полученных в качестве столбцов проекторов P i . Это, в свою очередь, требует знания расположения на многограннике его i -й вершины, j -го ребра и k -й грани, первоначально записанных в виде левых смежных классов группы G по стационарным подгруппам H p , H l и H s . Порядок вершин, ребер и граней на правильных многогранниках в R ³ находится при помощи графов их групп вращений. При построении графа группы в ней выбирают образующие элементы, в качестве вершин графа берут элементы группы и пользуются следующим правилом: движение, начинающееся в некоторой вершине, вдоль отрезка в направлении, указанном стрелкой, должно соответствовать умножению справа на связанный с этим отрезком образующий элемент [4, с. 68].

Некоторые из полученных нами результатов были известны и ранее. Однородные пространства, связанные с кубом в R ³ , рассматривали, например, Кириллов А.А. [5, с. 286– 288] и Винберг Э.Б. [6, с. 70]. На наш взгляд, использование формулы для проекторов P i на подпространства примарных компонент в Ind H E (см. теорему ниже) значительно облегчает нахождение геометрических описаний пространств неприводимых представлений. Отметим, что для этого нам вовсе нет необходимости знать сами операторы индуцированного представления. Единственное, что нам требуется – это знать проекторы R i на подпространства примарных компонент в каноническом разложении регулярного представления. Но эти проекторы легко вычисляются по формуле (4):

R i = nGr Е X® R ( s ) • (6) |G| _g _∈ _G

В таблицах, приводимых ниже, помимо словесного «геометрического» описания неприводимых представлений, мы даем матрицы операторов представлений для образующих элементов группы G . Исключение составляют лишь случаи кратного спектра (таких всего четыре). Этим случаям мы планируем посвятить отдельную работу.

2. Формула для проекционных операторов на пространства примарных компонент индуцированного представления IndGH E

Основной целью этого раздела является доказательство следующей теоремы.

Теорема 1. Пусть G — конечная группа, H — ее подгруппа, Ti — неприводимое комплексное представление группы G с характером χi . Пусть R – регулярное представление группы G и

R i =

dim T i |G|

52 X i ⁽ s ) R ⁽ s ) g ∈ G

– проекторы на пространства примарных компонент в каноническом разложении регулярного представления.

Тогда соответствующие проекторы для канонического разложения индуцированного представления Ind H E имеют вид

P i = MR i M t ,

HI где M = ||mij || - матрица размера (G : H) x |G|,

/ 1 , m ij = }0 ,

j ё X i , j / x i ,

где j – обозначение для j -го элемента группы G , x i – обозначение для i-го левого смежного класса G по H .

Доказательство. Рассмотрим операторы

= MR ( g ) M t .

H |

Покажем, что R h ( g ) — это операторы некоторого представления группы G , т.е. проверим условие гомоморфизма.

Лемма 1. Матрица M t M перестановочна с операторами R ( x ) .

Доказательство. Введем в группе G следующий порядок элементов: сначала перенумеруем элементы класса x 1 , затем — элементы класса x 2 и т.д. При такой нумерации элементов группы матрица M принимает наиболее простой вид:

/ 1 1 ... 1 0 0 ... 0 ... 0 0 ... 0

00 ... 011 ... 1 ... 00 ...0

M =

\ 0 0 ... 0 0 0 ... 0 ... 1 1 ...1

Тогда матрица M ^t M имеет блочно-диагональный вид, где на главной диагонали стоят квадратные матрицы I , все элементы которых равны 1.

Пусть |Н| = к. Разобьем матрицу R(x) на квадратные блоки Tij размера k x к. Покажем, что при выбранной нумерации элементов группы каждый такой блок представляет собой либо нулевую матрицу, либо матрицу подстановки. Воспользуемся тем, что R(x) - матрица подстановки и

^R ⁽ ^x ) ( ij ) = I

1 , если xj = i, 0 , если xj = i.

Пусть блок T ij ненулевой. Тогда существуют элементы g i h l Е x i и g j h m Е x j такие, что xg j h m = g i h l . Возьмем произвольный другой элемент g j h m ' E x j , h m ' = h m . Получим:

xg j h m ' = g i h l hm¹ g j ¹ g j h m ' = g i h l hm¹ h m ' = g i h l ' ё x i , где h l ' = h l .

Таким образом, τ ij — матрица подстановки.

Поскольку

I ■ ^T ij = ^T ij ' I =

0 ,

если блок τ ij ненулевой , если блок τ ij нулевой ,

то матрицы M t M и R ( x ) коммутируют. Лемма 1 доказана.

Покажем, что соответствие R h : g ^ R h ( g ) является представлением группы G .

R h ( g 1 ) R h ( g 2 ) = vL MR ( g 1 ) M t MR ( g 2 ) M t = { лемма 1 } =

^| ^н ¹ ²

1 w

MM t MR ( g 1 ) R ( g ₂ ) M t = {MM t = |H|E } =

—— MR ⁽ g 1 g 2 ) M t = ^r h ⁽ g 1 g 2 ) . ^| ^H |

Докажем, что представление R H есть не что иное, как индуцированное представление Ind H E .

Лемма 2.

tr( MR ( x ) M t ) = ^E 1 .

gEG g-1 xgEH

Доказательство. В процессе доказательства леммы 1 было установлено, что при соответствующей нумерации элементов группы матрица R(x) разбивается на (k х к)-блоки Tj. Тогда умножение слева на M равносильно суммированию строк матрицы R(x): сначала суммируются первые k строк, затем — последующие k строк и т.д. Аналогично, умножение справа на Mt приводит к такому же суммированию столбцов матрицы MR (x). В итоге tr(MR(x)Mt) = H| - E 1,

Xi EG/H xxi=xi т.е. след равен произведению порядка подгруппы на количество неподвижных смежных классов под действием x.

Пусть xi = giH. Тогда справедливы эквивалентности xxi = xi О xgiH = giH О Hg-1 xgiH E H О (giH)-1 xgiH E H О x-1 xxi E H.

Поэтому

I H\

E 1 = |H- E 1 .

x i E G/H xx i = x i

x i E G/H x _i ^- ¹ xx i E H

Возьмем элемент g E G со свойством g ^- ¹ xg E H и рассмотрим элемент д' = gh , h E H .

Имеем

( g ' ) ^- ¹ xg' = ( gh ) ^- ¹ xgh = h ^- ¹ g ^- ¹ xgh E H.

Таким образом, наряду с g , все элементы левого смежного класса gH обладают тем же свойством. Значит,

| HI- E 1= E 1. xiEG/H gEG xi-1xxiEH g-1xgEH

Лемма 2 доказана.

Покажем, что характеры представлений R h и Ind H E равны.

X R h ⁽ ^x ) = ^tr ^R H ⁽ ^x ) = pH7 ^tr( ^MR ⁽ ^x ) ^M t ) = { ^{лемма 2} } = -T H ^ ¹ = X Ind h e ⁽ ^x ) .

H H gEG g-1xgEH

По критерию изоморфизма представлений в терминах характеров

R h = Ind H E.

Воспользовавшись универсальной формулой для проекторов (4), получим

„ dim T i x

P i = \ G \ ^ X i ⁽ g ) ^r h ⁽ g ) =

^{1 1} g E G

G m TH ]T X i ( g ) MR ( g ) M ^t =

= ^T M I dim T i E xM R ( g ) I M ^t = tE MR,* ^t .

H G _gEG H

Теорема доказана.

Замечание 1. Если в группе G выбрать нумерацию элементов, отличную от используемой в доказательстве теоремы, то изменятся матрица M и проекторы R i , P i , но доказанная выше формула для проекторов останется справедливой. Покажем это.

Ассоциируем символ тильда с операцией изменения порядка элементов группы. Тогда

~ 1 _ —

Pi = h MRiMt, где Ri = C-1 Ri C, C - матрица перехода к новому базису. В итоге

P i = Hi mc - 1 R i CM t .

Достаточно ограничиться рассмотрением ситуации, когда только два элемента группы меняются местами. Возможны два случая. В первом случае меняются местами элементы из одного смежного класса (например, 1-й и 2-й). В этом случае

/0 1 0 ... 0\

100 ... 0

C =

001 ... 0

C - ¹ = C.

000 ... 0/

Во втором случае меняются местами элементы, принадлежащие различным смежным классам (например, к -й и ( к + 1)-й, k = \Н| ). Тогда минор

0 1

1 0

находится в матрице C на пересечении строк и столбцов с номерами к и к + 1. В обоих случаях C - ¹ = C . Поэтому

P i = — MCR i CM t .

Покажем, что в обоих случаях элементы

матрицы M подчиняются тому же правилу,

что и элементы матрицы M , т.е.

m ij =

1 ,

0 ,

1^^-

j е

x i

В первом случае имеем mi1 =

1 ,

1 е х і

0 ,

1 е х і

1 ,

0 ,

,^^-

2 е

2 /

x i

= m i 2 .

Аналогично, m i 2 = тп і 1 .

Во втором случае: m ik = тп i,k +1 , если i / { 1 , 2 } .

Ситуация, когда i е { 1 , 2 } , рассматривается аналогично.

Поскольку P i = S ^- ¹ P i S , S — аналог матрицы C , то

-^^^^

P i = SMC R i CM t S

- 1 .

Положив SMC = M , мы придем к уже доказанной формуле.

3. Реализации неприводимых представлений группы A4 в функциях на тетраэдре

В данном разделе и в последующих двух общая схема локализации неприводимых представлений, описанная во введении, применяется к группе вращений конкретного многогранника. Процесс локализации начинается с нахождения характеров, которыми с точностью до изоморфизма определяются неприводимые представления.

Таблица 1. Характеры неприводимых комплексных представлений группы A 4 [6]

w =

1 V 3 А

" 2+^ i)

^A 4	1 = e	2 = (12)(34) , 3 = (13)(24) , 4 = (14)(23)	5 = (123) , 6 = (134) , 7 = (142) , 8 = (243)	9 = (132) , 10 = (143) , 11 = (124) , 12 = (234)
T 1	1	1	1	1
T 2	1	1	w	w
T 3	1	1	w	w
T 4	3	–1	0	0

На рис. 1 указан порядок вершин, граней и ребер тетраэдра, найденный при помощи графа группы A 4 . Для построения графа мы выбираем образующие элементы 2 = (12)(34) (этот элемент порождает циклическую стационарную подгруппу ребер) и 8 = (243) (порождает циклическую стационарную подгруппу вершин или граней), в качестве вершин графа берем элементы группы и пользуемся правилом, что движение, начинающееся в некоторой вершине, вдоль отрезка в указанном стрелкой направлении соответствует умножению справа на связанный с этим отрезком образующий элемент.

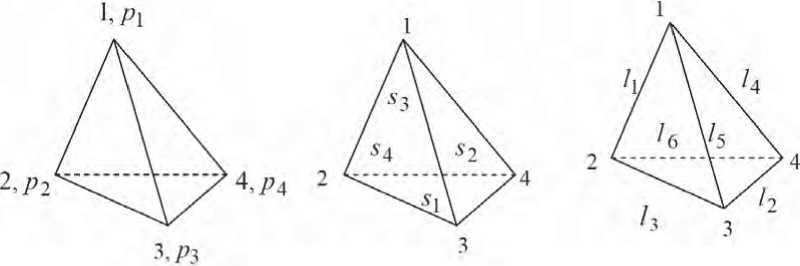
Рис. 1

Вершины, грани и ребра тетраэдра получаются в виде левых смежных классов по стационарным подгруппам:

P 1 = s 1 = { 1 , 8 , 12 },

P 2 = s 2 = { 2 , 5 , 11 },

P 3 = s 3 = { 3,6, 9}, p4 = s4 = {4, 7, 10},

1 1 = { 1 , 2 },

1 2 = { 3 , 4 },

1 3 = { 5 , 6 },

1 4 = { 7 , 8 },

1 5 = { 9 , 12 },

1 6 = { 10 , 11 }.

Спектральные разложения индуцированных представлений найдены с помощью таблицы характеров и формулы (5). Доказанная в разделе 2 теорема позволяет построить проекторы на пространства примарных компонент в каждом из случаев.

Случай вершин (граней) тетраэдра : Ind H p E = Ind H E = T 1 ф T 4 ,

P 1 = 4

1 1\

1 1

1 V

P 4

1 - 1

4 - 1

- 1

- 1 3

- 1

;

Случай ребер тетраэдра : Ind H E = T ₁ ф T 2 ф T 3 ф T 4 ,

(1111		1 ^	¹		1 w w w w \
	1111	1 1		1	1 w w w w
„ 1	1111	1 1	„ 1	ID ID 1 1 w w
P 1 = 7 6	1111	1 1	, P 2 = — , ² 6	ID ID 1 1 w w			^,
	1111	1 1		w w tD tD 1 1
\ 1111		1 1/	\ w w w w 1 1 /
/1 1			w w w	w \		/ ¹ ^-	1 0 0 0 0 \
		1 1	w w w	w D		- 1 1 0 0 0 0
„ 1		wo zD	11 w	w	„ 1	0 0 1 - 10 0
P ₃ = ^_ ³ 6		io w	11 w	w	, P^ = , ⁴ 2	0 0 - 110 0
		ww	ID w 1	1		0 0 0 0 1 - 1
ww			ID w 1	1	\ 0 0 0 0 -11)

Столбцы найденных проекторов, соответствующие их наибольшим ненулевым симметричным минорам, представляют собой искомые базисы в пространствах неприводимых представлений группы вращений тетраэдра. Эти базисы указаны в следующей таблице.

Таблица 2. Базисы в пространствах неприводимых представлений группы A 4

Вершины (грани) тетраэдра					Ребра тетраэдра
	T 1	T 4				T 1	T 2	T 3	T 4
p 1 ,s 1	1	3	–1	–1	l 1	1	1	1	1	0	0
p 2 ,s 2	1	–1	3	–1	l 2	1	1	1	–1	0	0
p 3 ,s 3	1	–1	–1	3	l 3	1	ID	w	0	1	0
p 4 ,s 4	1	–1	–1	–1	l 4	1	ID	w	0	–1	0
					l 5	1	w	ID	0	0	1
					l 6	1	w	ID	0	0	–1

Геометрический смысл полученных базисных функций на однородных пространствах тетраэдра становится понятным, если воспользоваться рис. 1. В таблице 3 указаны также матрицы операторов неприводимых представлений для образующих элементов в построенных базисах. Одномерные представления совпадают со своими характерами, а для нахождения матриц трехмерного представления T 4 мы воспользовались тем, что оно содержится в спектральных разложениях представлений Ind H E и Ind H E с кратностью 1. Поэтому с учетом формулы (1) ∀ g ∈ G справедливы равенства

^[ T 4 ⁽ g ) f i ]( P j ) = [ ^Ind H p E ⁽ g ) f i ] ⁽ P j ) = f i ( g ¹ p j ) ,

[T4(g)vi](lj) = [IndHE(g)vi](lj) = vi (g-1 lj), где fi — базисные функции в случае вершин тетраэдра, ϕi — базис в случае ребер.

Таблица 3. Описание неприводимых представлений группы A 4 (2 = (12)(34) и 8 = (243) — образующие элементы)

Неприводимые представления	Ребра тетраэдра	Вершины тетраэдра	Грани тетраэдра
T 1	функции-константы; T 1 (2) = T 1 (8) = 1
T 2	четные функции с нулевой суммой значений; T 2 (2) = 1 , T 2 (8) = w	не реализуются
T 3	четные функции с нулевой суммой значений; T 3 (2) = 1 , T 3 (8)= w	не реализуются
T 4	нечетные функции; / 1 0 0 \ T 4 (2) = 0 - 1 0 , \0 0 - 1/ / 0 0 1 \ T 4 (8) = - 1 0 0 , \ 0 - 10/	функции с нулевой суммой значений; / 0 1 - 1 \ T 4 (2) = 1 0 - 1 , \ 0 0 - 1/ / 1 0 - 1 \ T 4 (8) = 0 0 - 1 , \ 0 1 - 1/

Идентичность полученных локализаций неприводимых представлений для вершин и граней тетраэдра является проявлением его самодвойственности.

4. Реализации неприводимых представлений группы S4 в функциях на кубе

В этом разделе представлены результаты аналогичного применения общей конструкции локализации неприводимых представлений для группы вращений куба.

Таблица 4. Характеры неприводимых комплексных представлений группы S 4 [6, с.141]

S 4	1 = e	2 = (12)(34) , 3 = (13)(24) , 4 = (14)(23)	5 = (123) , 6 = (134) , 7 = (142) , 8 = (243) , 9 = (132) , 10 = (143) , 11 = (124) , 12 = (234)	13 = (12) , 14 = (34) , 15 = (13) , 16 = (24) , 17 = (14) , 18 = (23)	19 = (1324) , 20 = (1423) , 21 = (1234) , 22 = (1432) , 23 = (1243) , 24 = (1342)
T 1	1	1	1	1	1
T 2	1	1	1	–1	–1
T 3	2	2	–1	0	0
T 4	3	–1	0	1	–1
T 5	3	–1	0	–1	1

Порядок вершин, ребер и граней куба представлен на рис. 2.

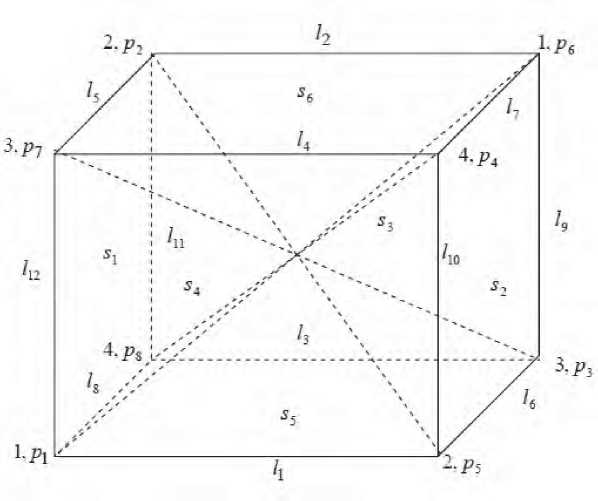
Рис. 2

Вершины, ребра и грани куба как левые смежные классы по стационарным подгруппам:

1 1 = { 1 , 13 },

1 2 = { 2 , 14 },

p 1 = { 1 , 8 , 12 }, p 2 = { 2 , 5 , 11 },

Р 3 = { 3 , 6 , 9 },

p 4 = { 4 , 7 , 10 }, p 5 = { 13 , 21 , 23 }, p 6 = { 14 , 16 , 18 }, p 7 = { 15 , 19 , 24 }, p 8 = { 17 , 20 , 22 },

1 3 = { 3 , 20 },

1 4 = { 4 , 19 }, s 1 = { 1 , 2 , 19 , 20 },

1 5 = { 5 , 15 }, s 2 = { 3 , 4 , 13 , 14 },

1 6 = { 6 , 21 }, s 3 = { 5 , 6 , 16 , 22 },

1 7 = { 7 , 16 }, s 4 = { 7 , 8 , 15 , 21 },

1 8 = { 8 , 22 }, s 5 = { 9 , 12 , 17 , 23 },

1 9 = { 9 , 18 }, s 6 = { 10 , 11 , 18 , 24 }.

1 10 = { 10 , 23 },

1 11 = { 11 , 17 },

1 12 = { 12 , 24 },

Спектральные разложения представлений, ассоциированных с однородными пространствами вершин, ребер и граней куба:

случай вершин куба : Ind H p E = T 1 ф T 2 ф T 4 ф T 5 ;

случай ребер куба (здесь уже появляется кратность 2) : Ind H E = T 1 ф T 3 ф 2 T 4 ф T 5 ;

случай граней куба : Ind H s E = T 1 ф T 3 ф T 5 .

Таблица 5. Базисы в пространствах неприводимых представлений группы S 4

Вершины куба
	T 1	T 2	T 4			T 5
p 1	1	1	3	–1	–1	3	–1	–1
p 2	1	1	–1	3	–1	–1	3	–1
p 3	1	1	–1	–1	3	–1	–1	3
p 4	1	1	–1	–1	–1	–1	–1	–1
p 5	1	–1	–1	3	–1	1	–3	1
p 6	1	–1	3	–1	–1	–3	1	1
p 7	1	–1	–1	–1	3	1	1	–3
p 8	1	–1	–1	–1	–1	1	1	1

Ребра куба
	T 1	T 3		T 4	T 5
l 1	1	2	–1		2	0	–1
l 2	1	2	–1	Ри н	–2	0	1
l 3	1	2	1	к	0	2	–1
l 4	1	2	–1	и ti	0	–2	1
l 5	1	–1	2		–1	–1	–2
l 6	1	–1	2	Н Я	1	1	–2
l 7	1	–1	2	м	–1	–1	0
l 8	1	–1	2	н CD	1	1	0
l 9	1	–1	–1	S	–1	1	–1
l 10	1	–1	–1		1	–1	–1
l 11	1	–1	–1	Я	–1	1	1
l 12	1	–1	–1		1	–1	1

Грани куба
	T 1	T 3		T 5
s 1	1	2	–1	1	0	0
s 2	1	2	–1	–1	0	0
s 3	1	–1	2	0	1	0
s 4	1	–1	2	0	–1	0
s 4	1	–1	2	0	–1	0
s 6	1	–1	–1	0	0	–1

Таблица 6. Описание неприводимых представлений группы S 4 (8 = (243) и 13 = (12) — образующие элементы)

Неприводимые представления	Вершины куба	Ребра куба	Грани куба
1	2	3	4
T 1	функции-константы; T 1 (8) = T 1 (13) = 1
T 2	нечетные функции с нулевой суммой значений на вершинах принадлежащих одной грани; T 2 (8) = 1 , T 2 (13) = w	не реализуется
T 3	не реализуется	четные функции с нулевой суммой значений;	четные функции с нулевой суммой значений;

1	2	3	4
		T . < ⁸ >= ( ° - ; ) ^т > < ¹³ >-С - 1)	^т » < ⁸ >= ( - 1 0 ) ^т > ^(13)-( о - 0
T 4	четные функции с нулевой суммой значений и с суммой значений нуль на вершинах, принадлежащих одной грани; ⁽ 1 0 - 1 \ T 4 (8) = 0 0 - 1 , У 0 1 - 1/ ⁽ 0 1 0 \ T 4 (13) = 1 0 0 У 0 0 1/	возникает кратный спектр	не реализуется
T 5	нечетные функции; ⁽ 1 - 1 0 \ T 5 (8) = 0 - 1 1 , У 0 - 1 0/ ⁽ 0 - 1 0 \ т 5 (13) = - 1 0 0 У 0 0 - 1/	нечетные функции; ⁽ 1 0 0 \ т 5 (8) = 1 0 - 1 , У 1 1 - 1/ ⁽ 1 0 - 1\ т 5 (13) = 0 - 1 0 У 0 0 - 1/	нечетные функции; ⁽ 0 - 1 0 \ т 5 (8) = 0 0 - 1 , У 10 0 / ⁽ - 10 0 \ т 5 (13) = 0 0 - 1 У 0 - 1 0 /

5. Реализации неприводимых представлений группы A5 в функциях на додекаэдре

В данном разделе приводятся результаты применения общей конструкции локализации неприводимых представлений для группы вращений додекаэдра. В этом случае наименьшие размеры проекторов составляют 12 х 12, а спектры индуцированных представлений содержат кратности 2 и 3.

Таблица 7. Характеры неприводимых комплексных представлений группы A 5 [6, с.76]

/ 1 + V 5

a =

У 2

ь =

1	2	3	4	5	6
^A 5	1 = e	2 = (123) ,	22 = (12345) ,	23 = (12354) ,	46 = (12)(34) ,
		3 = (124) ,	25 = (12453) ,	24 = (12435) ,	47 = (12)(35) ,
		4 = (125) ,	26 = (12534) ,	27 = (12543) ,	48 = (12)(45) ,
		5 = (132) ,	29 = (13254) ,	28 = (13245) ,	49 = (13)(24) ,
		6 = (134) ,	30 = (13425) ,	31 = (13452) ,	50 = (13)(25) ,
		7 = (135) ,	33 = (13542) ,	32 = (13524) ,	51 = (13)(45) ,
		8 = (142) ,	34 = (14235) ,	35 = (14253) ,	52 = (14)(23) ,
		9 = (143) ,	37 = (14352) ,	36 = (14325) ,	53 = (14)(25) ,
		10 = (145) ,	38 = (14523) ,	39 = (14532) ,	54 = (14)(35) ,
		11 = (152) ,	41 = (15243) ,	40 = (15234) ,	55 = (15)(23) ,
		12 = (153) ,	42 = (15324) ,	43 = (15342) ,	56 = (15)(24) ,
		13 = (154) ,	45 = (15432)	44 = (15423)	57 = (15)(34) ,
		14 = (234) ,			58 = (23)(45) ,
		15 = (235) ,			59 = (24)(35) ,
		16 = (243) ,			60 = (25)(34)

1	2	3	4	5	6
		17 = (245) , 18 = (253) , 19 = (254) , 20 = (345) , 21 = (354)
T 1	1	1	1	1	1
T 2	3	0	a	b	–1
T 3	3	0	b	a	–1
T 4	4	1	–1	–1	0
T 5	5	–1	0	0	1

Порядок вершин, ребер и граней додекаэдра представлен на рис. 3

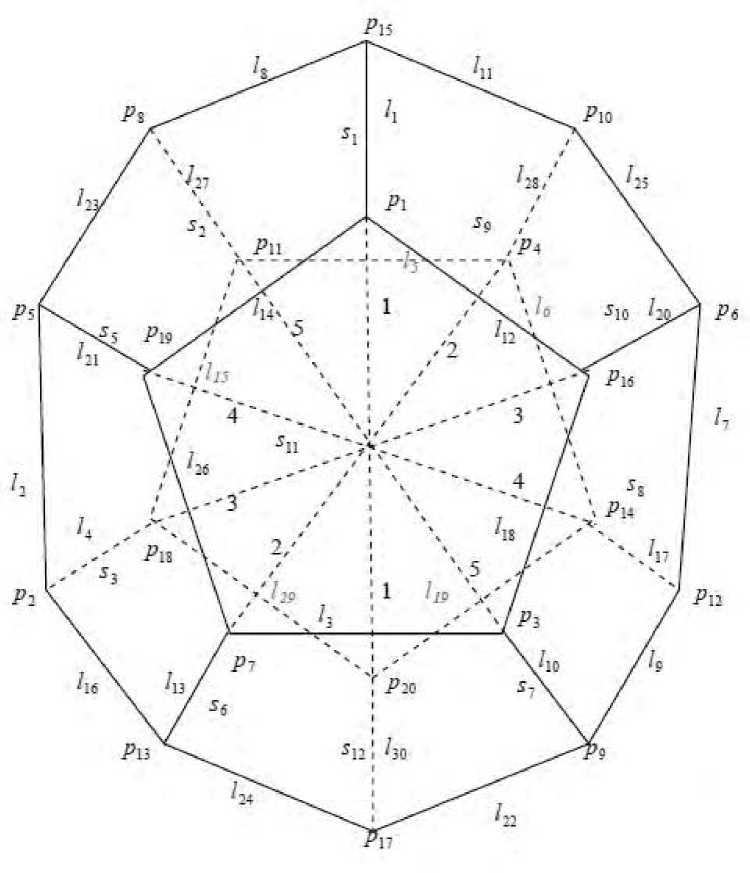
Рис. 3

Вершины, грани и ребра додекаэдра как левые смежные классы по стационарным подгруппам:

p i = {1, 15, 18}, p 2 = { 2, 4, 47 }, p3 = {3, 23, 26}, p4 = {5, 7, 50}, p5 = {6, 29, 32}, p6 = {8,34, 35}, p7 = {9, 36, 37}, p 8 = {10,38,39}, p 9 = {11,12,55}, pio = {13, 40, 42 },

p ii = { 14 , 19 , 59 }, p 12 = { 16 , 21 , 60 }, p із = { 17 , 20 , 58 }, p 14 = { 22 , 25 , 48 }, p 15 = { 24 , 27 , 46 }, p 16 = { 28 , 31 , 51 }, p 17 = { 30 , 33 , 49 }, p 18 = { 41 , 45 , 57 }, p 19 = { 43 , 44 , 56 }, p 20 = { 52 , 53 , 54 },

s 1 = { 1 , 22 , 32 , 35 , 45 }, s 2 = { 2 , 13 , 31 , 36 , 59 }, s 3 = { 3 , 18 , 33 , 38 , 57 }, s 4 = { 4 , 21 , 39 , 40 , 49 }, s 5 = { 5 , 20 , 24 , 44 , 53 }, s 6 = { 6 , 19 , 25 , 37 , 55 }, s 7 = { 7 , 8 , 26 , 41 , 58 }, s 8 = { 9 , 15 , 30 , 42 , 48 }, s 9 = { 10 , 16 , 23 , 43 , 50 }, s 10 = { 11 , 14 , 27 , 28 , 54 }, s 11 = { 12 , 17 , 29 , 34 , 46 }, s 12 = { 47 , 51 , 52 , 56 , 60 },

1 1 = { 1 , 46 },

1 2 = { 2 , 6 },

1 3 = { 3 , 9 },

1 4 = { 4 , 57 },

1 5 = { 5 , 14 },

1 6 = { 7 , 22 },

1 7 = { 8 , 16 },

1 8 = { 10 , 24 },

1 9 = { 11 , 60 },

1 1o = { 12 , 26 },

1 11 = { 13 , 27 },

1 12 = { 15 , 31 },

1 13 = { 17 , 37 },

1 14 = { 18 , 43 },

1 15 = { 19 , 45 },

1 16 = { 20 , 47 },

1 17 = { 21 , 48 },

1 18 = { 23 , 51 },

1 19 = { 25 , 54 },

1 20 = { 28 , 34 },

1 21 = { 29 , 44 },

1 22 = { 30 , 55 },

1 23 = { 32 , 38 },

1 24 = { 33 , 58 },

1 25 = { 35 , 42 },

1 26 = { 36 , 56 },

1 27 = { 39 , 59 },

1 28 = { 40 , 50 },

1 29 = { 41 , 53 },

1 30 = { 49 , 52 }.

Спектральные разложения индуцированных представлений:

случай вершин додекаэдра: IndHpE = T1 ф T2 ф T3 ф 2T4 ф T5, случай ребер додекаэдра: IndH E = T1 ф T2 ф T3 ф 2T4 ф 3T5, случай граней додекаэдра: IndH E = T1 ф T2 ф T3 ф T5.

Таблица 8. Базисы в пространствах неприводимых представлений группы A 5 ( r = V5)

Вершины додекаэдра
	T 2			T 3			T 5
p 1	3	–1	1	3	–1	1	3	–1	–1	–1	–1
p 2	–1	3	–1	–1	3	–1	–1	3	–1	–1	1
p 3	1	–1	3	1	–1	3	–1	–1	3	1	–1
p 4	–1	–1	r	–1	–1	-r	–1	–1	1	3	–1
p 5	1	-r	–1	1	r	–1	-1	1	–1	–1	3
p 6	1	–3	1	1	–3	1	–1	3	–1	–1	1
p 7	1	1	-r	1	1	r	–1	–1	1	3	–1
p 8	1	1	r	1	1	-r	–1	–1	1	–1	1
p 9	–1	–1	-r	–1	–1	r	–1	–1	1	–1	1
p 10	1	r	–1	1	-r	–1	–1	1	–1	1	–1
p 11	–1	1	–3	–1	1	–3	-1	–1	3	1	–1
p 12	–1	r	1	–1	-r	1	–1	1	–1	–1	3
p 13	–1	-r	1	–1	r	1	–1	1	–1	1	–1
p 14	r	–1	–1	-r	–1	–1	1	–1	–1	1	1
p 15	-r	–1	–1	r	–1	–1	1	–1	–1	–1	–1
p 16	-r	r	-r	r	-r	r	1	1	1	–1	–1
p 17	r	1	1	-r	1	1	1	–1	–1	–1	–1
p 18	r	-r	r	-r	r	-r	1	1	1	–1	–1
p 19	-r	1	1	r	1	1	1	–1	–1	1	1
p 20	–3	1	–1	–3	1	–1	3	–1	–1	–1	–1

Грани додекаэдра
	T 2			T 3			T 5
s 1	r	–1	1	r	1	–1	5	–1	–1	–1	–1
s 2	–1	r	–1	1	r	1	–1	5	–1	–1	–1
s 3	1	–1	r	–1	1	r	–1	–1	5	–1	–1
s 4	–1	1	1	1	–1	–1	–1	–1	–1	5	–1
s 5	–1	–1	–1	1	1	1	–1	–1	–1	–1	5
s 6	1	1	–1	–1	–1	1	–1	–1	–1	–1	–1
s 7	1	-r	1	–1	-r	–1	–1	5	–1	–1	–1
s 8	1	1	1	–1	–1	–1	–1	–1	–1	–1	5
s 9	–1	–1	1	1	1	–1	–1	–1	–1	–1	–1
s 10	–1	1	-r	1	–1	-r	–1	–1	5	–1	–1
s 11	1	–1	-1	–1	1	1	–1	–1	–1	5	–1
s 12	-r	1	–1	-r	–1	1	5	–1	–1	–1	–1

Ребра додекаэдра

T 2

l 1	2	0	0	l 11	b	a	–1	l 21	1	b	-a
l 2	0	2	0	l 12	b	a	1	l 22	-b	a	1
l 3	0	0	2	l 13	a	1	b	l 23	1	b	a
l 4	–1	b	a	l 14	b	-a	1	l 24	-b	-a	1
l 5	0	0	–2	l 15	a	1	-b	l 25	1	-b	a
l 6	a	–1	-b	l 16	–1	b	-a	l 26	-a	1	b
l 7	0	–2	0	l 17	–1	-b	a	l 27	-a	1	-b
l 8	b	-a	–1	l 18	-a	–1	b	l 28	-a	–1	-b
l 9	–1	-b	-a	l 19	-b	a	–1	l 29	-b	-a	–1
l 10	a	–1	b	l 20	1	-b	-a	l 30	–2	0	0
T 3
l 1	2	0	0	l 11	a	b	–1	l 21	1	a	-b
l 2	0	2	0	l 12	a	b	1	l 22	-a	b	1
l 3	0	0	2	l 13	b	1	a	l 23	1	a	b
l 4	–1	a	b	l 14	a	-b	1	l 24	-a	-b	1
l 5	0	0	–2	l 15	b	1	-a	l 25	1	-a	b
l 6	b	–1	-a	l 16	–1	a	-b	l 26	-b	1	a
l 7	0	-2	0	l 17	–1	-a	b	l 27	-b	1	-a
l 8	a	-b	–1	l 18	-b	- 1	a	l 28	-b	–1	-a
l 9	–1	-a	-b	l 19	-a	b	–1	l 29	-a	-b	–1
l 10	b	–1	a	l 20	1	-a	-b	l 30	–2	0	0

Таблица 9. Описание неприводимых представлений группы A 5 (22 = (12345) и 46 = (12)(34) — образующие элементы)

Неприводимые представления	Вершины додекаэдра	Грани додекаэдра	Ребра додекаэдра
1	2	3	4
T 1	функции-константы; T 1 (22) = T 1 (46) = 1
T 2	нечетные функции: / 2 - 1 2 \ T 2 (22) = — 5 1 b 1 a 1 , -a - 1 -b / 2 -b 0 \ T 2 (46) = - — 1 a - 2 0 1 , у b a — 5 /	нечетные функции: / 1 0 -b \ T 2 (22) = 1 0 0 1 1 , 0 - 1 -b / -b - 1 0 \ T 2 (46) = 1 b b 0 1 , - 1 -b - 1	нечетные функции: a 1 -b T 2 (22) = 2 1 - 1 -b a 1 , -b -a 1 / 10 0 \ T 2 (46) = 0 - 1 0 , У 0 0 - 1/
T 3	нечетные функции: / 2 - 1 2 \ T з (22) =--- a 1 b , V⁵ \ -b - 1 -a) ( 2 -a 0 \ T 3 (46) = — b - 2 0 , *⁵ y -a -b -— 5/	нечетные функции: / 1 0 -a \ T з (22) = 0 0 1 , У0 - 1 -a/ / -a - 1 0 \ T з (46) = a a 0 , - 1 -a - 1	нечетные функции: b 1 -a T 3 (22) = 2 1 - 1 -a b 1 , -a -b 1 / 10 0 \ T 3 (46) = 0 - 1 0 , У 0 0 - 1/
T 4	возникает кратный спектр	не реализуется	возникает кратный спектр
T 5	четные функции с нулевой суммой значений:	четные функции с нулевой суммой значений:	возникает кратный спектр

1	2	3	4
	^⎛ 11 - 1 - 10 ^⎞	^⎛ 1000 - 1 ^⎞
	^⎜ 01 - 1 - 11 ^⎟	0001 - 1 ^⎟
	T ₅ (22) = 0 1 - 1 0 0 ,	T 5 (22) = 0 1 0 0 - 1 ,
	^⎜ 10 - 1 - 10 ^⎟	^⎜ 0000 - 1 ^⎟
	10 - 100	0010 - 1
	^⎛ - 10000 ^⎞	^⎛ 0 - 1010 ^⎞
	^⎜ - 10001 ^⎟	^⎜ 0 - 1000 ^⎟
	T ₅ (46) = - 1 0 1 0 0 ,	T 5 (46) = 0 - 1 1 0 0 ,
	^⎜ - 10010 ^⎟	^⎜ 1 - 1000 ^⎟
	- 11000	0 - 1001

Поскольку индуцированные представления Ind H и Ind H 5 E содержат кратные точки, интерес представляет нахождение несложного алгоритма их разделения в случае представлений типа Ind H E , а также обобщение полученных результатов на правильные многогранники в R ⁴ и на индуцированные представления групп Ли. В трехмерном случае все стационарные подгруппы циклические, и канонические разложения возникающих индуцированных представлений содержат кратности. В четырехмерном случае аналогичным методом мы исследовали представления групп вращений симплекса и куба, ассоциированные с однородными пространствами к -граней ( к = 0 , 1 , 2 , 3). Специфика R 4 такова, что стационарные подгруппы здесь неабелевы, и проблема разделения изоморфных компонент не возникла. Кроме того, вычисления показали, что в случае R ⁴ невозможно локализовать все неприводимые представления групп вращений симплекса и куба, разлагая представления, связанные только с однородными пространствами к -граней.

Список литературы Геометрические реализации неприводимых представлений групп вращений правильных многогранников в трехмерном пространстве

Фробениус Ф.Г. Теория характеров и представлений групп. М.: КомКнига, 2005
Cartan E´. Sur la determination d’un systeme orthogonal complet dans un espase de Riemann symmetrique clos. Rend. Circ. Mat., Palermo, 1929
Серр Ж.-П. Линейные представления конечных групп. М.: Мир, 1970
Гроссман И., Магнус В. Группы и их графы. М.: Мир, 1971
Кириллов А.А. Элементы теории представлений. М.: Наука, 1978
Винберг Э.Б. Линейные представления групп. М.: Наука, 1985

Статья научная